一種改進的機載武器傳遞對準中桿臂效應動態補償方法*

谷 雨,司 帆,趙 剡,張亞崇,3

(1 西安飛行自動控制研究所,西安 710065;2 北京航空航天大學儀器科學與光電工程學院,北京 100191;3 飛行器控制一體化技術國防科技重點實驗室,西安 710065)

0 引言

傳遞對準是機載武器在發射之前的一項重要的初始化工作,其對準精度在很大程度上決定了武器的使用效能[1]。在以往的研究工作中,通常將桿臂矢量看作是固定值,直接在主慣導信息上進行剛性桿臂補償后作為子慣導的導航參數,當機翼發生結構撓曲變形時,主慣導的精度再高,也會被淹沒在由撓曲變形引起的誤差中[2],顯然該方法沒有考慮桿臂效應的產生機理,不能滿足高性能的應用需求;此外,很多研究文獻將機翼結構動態變形理想化為二階或三階馬爾科夫過程[3],模型的有關參數全憑經驗設定,缺乏實用性[4]。

針對傳遞對準中桿臂效應動態補償這一技術難題,文中提出了一種桿臂效應的動態補償方案:利用撓曲變形估計出桿臂矢量的變化情況,進而對桿臂速度進行補償,消除由桿臂效應對傳遞對準的影響。通過“速度+姿態”匹配的仿真結果表明,該方法可有效提高傳遞對準的精度,并且具有良好的工程實現上的便利性。

1 機翼撓曲變形模型

1.1 撓曲變形

由于實際飛行環境的復雜多樣性,機翼的撓曲變形具有時變特征且與機型強相關,是無法準確預測的。由于撓曲變形角可看作是隨機作用力影響下的隨機變量,為了研究的方便,文中將撓曲變形角建模為白噪聲激勵下的二階馬爾科夫過程,其模型如下[5]:

(1)

(2)

式中:θ=[θx,θy,θz]T為撓曲變形角;ω=[ωx,ωy,ωz]T為撓曲變形角速率;β=diag(βx,βy,βz)為參數矩陣;ηf=[ηfx,ηfy,ηfz]T為白噪聲,其頻譜密度Qη為:

Qη=4β3σ2

(3)

1.2 撓曲位移

受撓曲變形角的影響,子慣導會偏離其標稱桿臂矢量位置,從而產生撓曲位移。下面以XOZ平面為例,分析撓曲變形角與撓曲位移的關系。圖1為機翼撓曲變形示意圖。R為子慣導的實際桿臂矢量,Rf為子慣導的撓曲位移向量,OmXmZm為主慣導處的載體系,OsXsZs為子慣導處的載體系,Lx為主、子慣導標稱桿臂矢量的X軸分量,θy為繞機體縱軸的撓曲變形角。當θy為小角度時,機翼可看作是一段均勻的圓弧,一般可將B點視作線段OA的中點。

根據圖中幾何關系可得:

θy=2∠BOmOs

(4)

(5)

∠BOmOs+∠BOsOm+∠BOsA+∠BAOs=180°

(6)

聯立式(5)、式(6)可得:

∠BOsOm+∠BOsA=90°

(7)

即∠OmAOs為直角,則撓曲位移向量Rf可表示為:

(8)

取小角度近似條件sinθ≈θ,cosθ≈1,則式(8)可簡化為:

(9)

同理,擴展到XOY和YOZ平面,Rf可表示為:

(10)

經過撓曲位移補償后,實際桿臂矢量可表示為:

R=L+Rf

(11)

以上建立了機翼撓曲變形影響下桿臂矢量的變化模型,通過式(11)可對傳遞對準中的桿臂效應進行補償。

2 動態桿臂效應的分析

如前所述,由于桿臂矢量不再是常值,桿臂效應也變得更加復雜。為了能夠精確補償,這里對動態桿臂矢量影響下的桿臂效應進行詳細分析。

圖2中,Rm和Rs分別為主、子慣導在地球系的位置矢量,R為桿臂矢量。根據圖中矢量關系可得:

Rs=Rm+R

(12)

由于慣導輸出的速度是相對于地球的,將式(12)相對于地球系求一階導數,并根據哥氏定理可得:

(13)

式中:e表示地球系;m表示主慣導載體系。將式(13)投影至地理系(t系)可得:

(14)

將式(12)相對慣性系求二階導數,可得到主、子慣導的比力關系:

(15)

(16)

(17)

式中:fm和fs分別為主、子慣導加速度計的比力;gm和gs分別為主、子慣導處的重力加速度。

將式(15)投影至主慣導載體系,并考慮到gm與gs近似相等[6],可得:

(18)

3 速度+姿態匹配對準模型

本節以“速度+姿態”匹配傳遞對準為例,詳細說明如何在對準模型中對撓曲變形進行處理的方法。

3.1 狀態方程

系統狀態變量取為:

(19)

則系統狀態方程可寫為[4,7]:

(20)

式中:系統矩陣F為:

(21)

系統噪聲為:

(22)

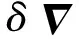
噪聲矩陣為:

(23)

3.2 量測方程

由于主慣導的精度遠高于子慣導,因此可認為主慣導是無誤差的。取姿態匹配量測陣為[8]:

(24)

受撓曲變形角θ與安裝誤差角ξ的影響,主、子慣導坐標系之間的關系如圖3所示。因此,姿態量測矩陣可分解為:

(25)

考慮到φ、ξ、θ都是小角度,則:

(26)

(27)

(28)

將式(26)～式(28)代入式(25),并忽略二階小量,可得:

(29)

取姿態匹配量測量為:

(30)

則量測方程為:

(31)

速度匹配的量測量為:

(32)

(33)

聯立式(14)和式(33),可得:

(34)

聯立式(31)和式(34),可得速度+姿態匹配的量測方程:

Z=HX+v

(35)

式中：Z=[φ,δV]T為量測向量;v為量測噪聲;量測矩陣H為:

(36)

4 仿真結果與分析

4.1 仿真條件

文中所采用的仿真軌跡如圖4所示。起點的經緯度和高度為:116.11°E、40.05°N、5 000 m。初始俯仰角、橫滾角和航向角分別為:0°、0°、30°。初始速度為200 m/s。AB段為S型轉彎,飛行時間60 s;BC段勻速平飛,飛行時間120 s;CD段U型轉彎,飛行時間90 s;DE段勻速平飛,飛行時間240 s。

主慣導數據由軌跡發生器直接得到。在主慣導基礎上,考慮到主、子間安裝誤差角、撓曲變形角,并疊加器件誤差后得到子慣導的實際數據。子慣導陀螺儀常值漂移和隨機漂移均為0.1°/h,加速度計常值零偏和隨機零偏均為100 μg,安裝誤差角為ξ=[1°,1°,1°]T,撓曲變形角在3個軸向上的方差為[0.2°,0.5°,0.2°]T,相關時間均為30 s。子慣導姿態誤差初值為[1°,2°,3°]T,子慣導解算周期為10 ms,濾波周期為50 ms。

4.2 結果分析

仿真得到的姿態誤差估計曲線如圖5～圖7所示。圖中實線表示未補償桿臂效應時的姿態估計誤差,虛線表示補償了桿臂效應后的姿態估計誤差。從圖中可看出,經過補償后,姿態誤差明顯減小。在完成S型轉彎后(60 s)的誤差統計結果如表1所示。無論是均值還是均方根誤差(RMSE)均得到了明顯的改善。尤其是對于航向角,其誤差均值由-7.8′減小到了-3.8′。

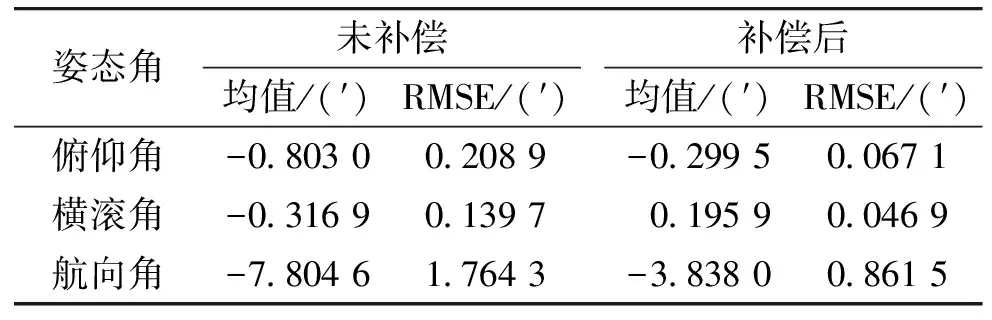
表1 姿態誤差統計結果

5 結論

文中針對機翼撓曲變形影響下的桿臂矢量變化,詳細推導了桿臂效應的產生機理,并提出了一種改進的桿臂效應動態補償方法。與傳統方法相比,該方法中桿臂矢量不再是一常值,而是隨著撓曲變形不斷變化。在此基礎上,結合“速度+姿態”匹配傳遞對準模型對文中所提出的方法進行了驗證。仿真結果表明,在補償桿臂效應后,子慣導姿態誤差估計精度明顯提高,同時該方法也便于工程實現。