船舶輔機雙層半主動非線性隔振系統振動特性分析
包國治,周馬俊,薛 斌,薛 晨,夏兆旺
(江蘇科技大學 能源與動力學院,江蘇 鎮江 212003)
0 引 言
“21世紀海上絲綢之路”的提出為船舶行業發展提供了機遇,也提出了更高的挑戰。在軍用領域,為維護我國海洋權益需要建設一批高性能的艦船,而艦船的隱身能力是衡量其性能的重要指標,尤其是潛艇,所以對艦船的減振降噪至關重要[1-3];在民用領域,隨著游艇產業的快速發展,對船舶的舒適性提出了更高的要求,船舶的振動噪聲水平是衡量其舒適性的核心指標[4-5]。
低速巡航工況下,船舶輻射噪聲能量的約70%是由其內部主、輔機和軸系運轉引起的[6-7]。輻射噪聲主要由機械設備的振動通過基座、管路激勵殼體產生。雙層隔振裝置是連接主、輔機系統與基座的重要結構,對振動在主、輔機與基座之間的傳遞以及船舶機械噪聲有著重要的影響[8-9]。因此,研究雙層隔振系統的振動特性,降低主、輔機的振動向基座傳遞,從而降低船舶的輻射噪聲,對于提高船舶聲學安靜性能具有重要意義。
為進一步提高傳統被動雙層隔振系統的隔振效果,各國學者開始探索船舶輔機雙層半主動隔振裝置。磁流變阻尼器是一種典型的半主動控制裝置,它具有響應快、能耗低等優點[10]。已被廣泛應用于橋梁、土木、機械和汽車等領域的減振降噪。
為深入研究船舶輔機雙層隔振系統的主共振特性,本文建立了基于磁流變阻尼技術的船舶輔機雙層半主動非線性隔振系統動力學方程,分析其主共振特性,采用平均法研究半主動非線性隔振系統的穩態響應,研究半主動非線性隔振系統參數對隔振效果的影響規律,并對理論解進行數值驗證,為進一步有效控制船舶輔機雙層隔振系統的主共振奠定了理論基礎。
1 磁流變阻尼器力學模型
為描述磁流變阻尼控制系統的滯后特性,本文采用一種修正的Bingham模型,如圖1所示,其表達式為

其中:FMRD為磁流變阻尼器的阻尼力,Fy為磁流變阻尼器的控制力,V為磁流變阻尼器活塞與柱筒之間的相對速度,C1為磁流變阻尼器的粘性阻尼系數,V0為磁流變阻尼器的零力速度。模型中的位置參數可以通過實驗數據擬合得到。
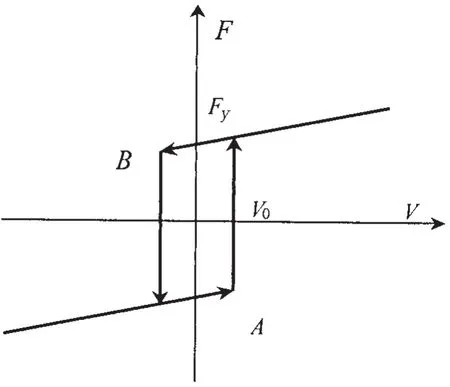
圖1 MR阻尼器的修正Bingham模型Fig.1 The modified Bingham model of MRD
2 輔機雙層半主動非線性隔振系統模型
輔機雙層半主動非線性隔振系統如圖2所示,系統的運動方程為

其中:F=F0cos( ωt)為輔機激振力;)為磁流變阻尼力,Fy為控制力,V0為磁流變阻尼器的零力速度;m1為中間質量塊質量,m2為輔機質量,k1為下層剛度,k2為上層剛度,y1為下層位移,y2為上層位移,C1為磁流變阻尼器阻尼系數,C2為上層隔振器的阻尼系數。
3 輔機單層半主動非線性隔振系統的主共振
取無量綱位移x1=y1k2/F0,x2=y2k2/F0,無量綱時間 τ=ωt,對(2)式進行無量綱化可得
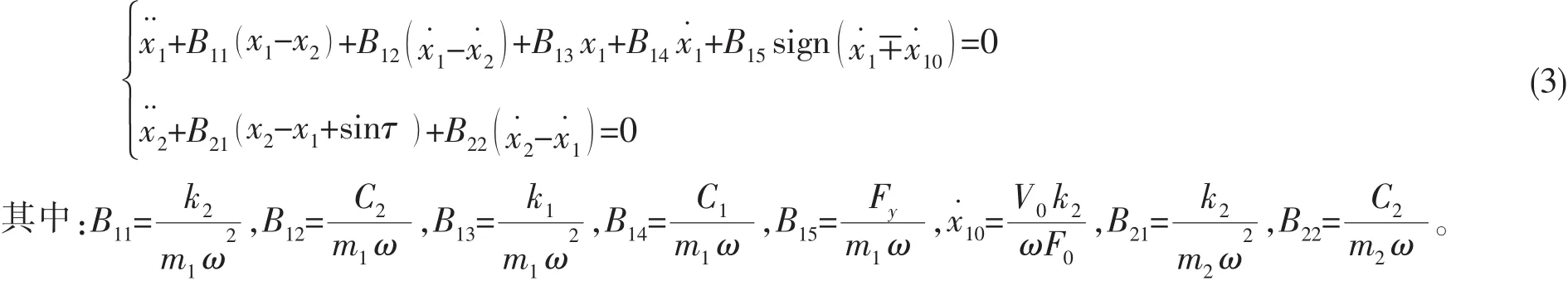
(3)式中非線性系數B15與其它項系數相比是小值,因此,是一個弱非線性系統。用非線性振動理論中的平均法求解系統響應,設其解為

其中:φi=τ-θi。 對(4)式求導并與(3)式聯立,可得
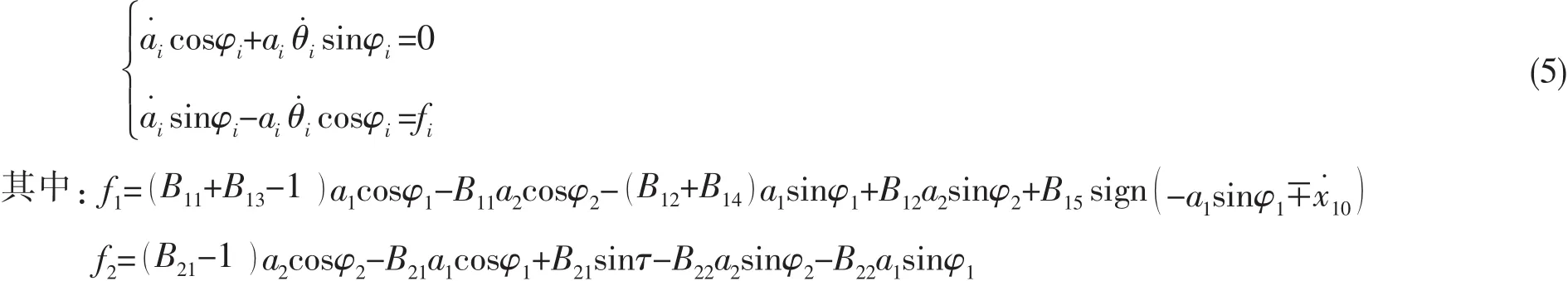
由(5)式可解得

對(6)式進行 K-B 變換,并利用 φ1-φ2=θ2-θ1,可得系統的平均方程:
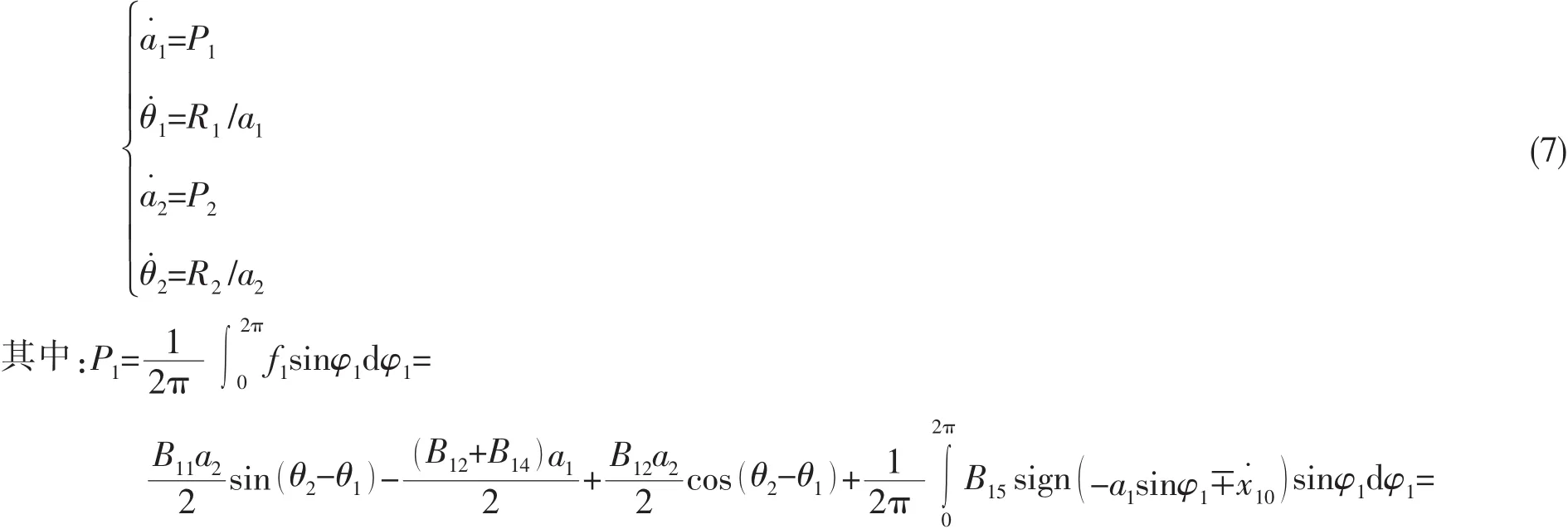
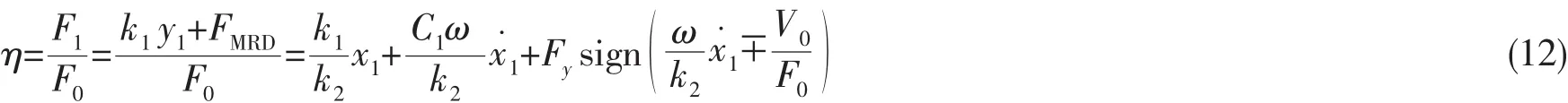
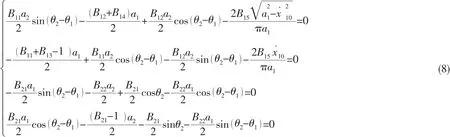
將(8)式的第 1,2 式中 sin( θ2- θ1),cos( θ2- θ1)項移到右側平方相加得到
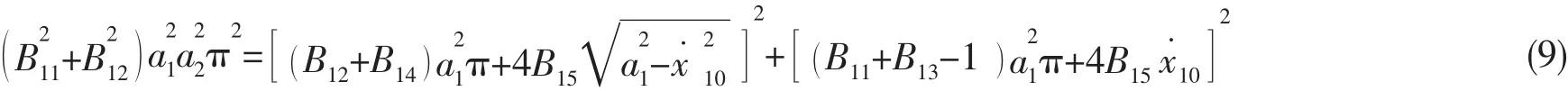
由(8)式的第 1,2 式中解出 sin( θ2- θ1),cos( θ2- θ1)。 將(8)式的第 3,4 式中 sinθ2,cosθ2項移到右側平方相加,然后將 sin( θ2- θ1),cos( θ2- θ1)代入,可得到
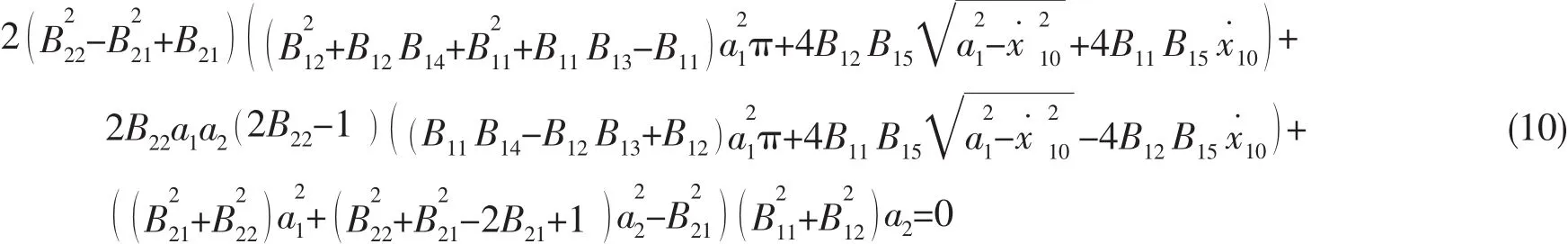
聯立(9)式和(10)式即可解出系統穩態響應的振幅a1及a2。 將(8)式的第 3,4 式中 sin( θ2- θ1),cos(θ2- θ1)項移到右側平方相加,并將a1及a2代入式中即可解得系統穩態響應的相位 θ2,θ1。從而可得到系統穩態響應的一次近似解:

輔機雙層隔振系統的振動傳遞率為
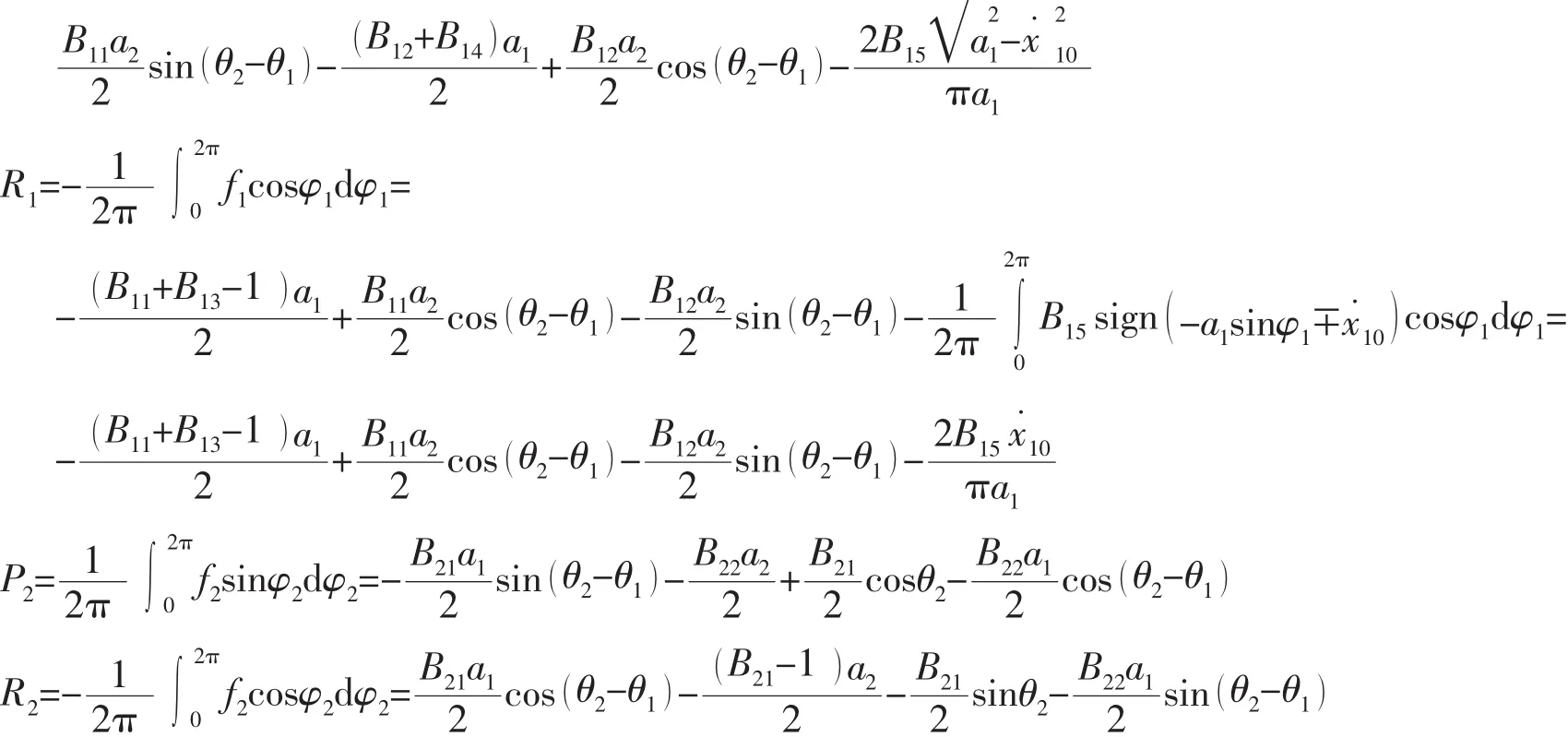
將(11)式中x1求導代入(12)式得到
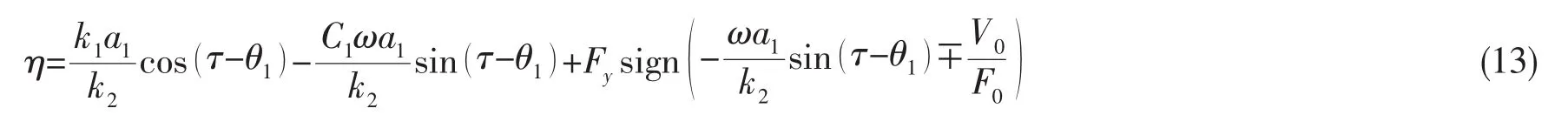
4 輔機雙層半主動非線性隔振系統振動特性分析
輔機雙層半主動非線性隔振系統主要參數選為:輔機質量m2=600 kg,中間質量塊質量m1=354 kg,磁流變阻尼器的零力速度V0=0.1 m/s,隔振系統的下層彈簧剛度k1=8.1×105N/m,上層彈簧剛度k2=6.4×105N/m,磁流變阻尼器的阻尼系數C1=2 000 Ns/m,上層阻尼C2=3 100 Ns/m,半主動系統的控制力幅值Fy=20 N,激振力幅值F0=200 N。 初始條件取x1=0,x˙1=0。
輔機雙層半主動非線性隔振系統的運動學方程如(3)式所示,初始條件取x1=0,x˙1=0,用Maple對(3)式進行數值積分,可得到其數值解。為驗證采用平均法得到的輔機雙層半主動非線性隔振系統理論解的正確性,將采用平均法得到的理論解與Maple仿真得到的數值解進行了對比,如圖3所示。由圖3可以看出:理論解和數值解基本一致,表明采用平均法得到半主動非線性隔振系統的理論解是正確的。
為研究輔機雙層隔振系統的隔振效果,先計算出穩態響應時中間質量塊的速度和位移,進而求出傳遞到基座的力,然后得到輔機的振動傳遞率曲線。本文主要研究磁流變阻尼力模型中的三個參數C1、V0和Fy對輔機雙層隔振系統振動傳遞率的影響。磁流變阻尼器主要參數對輔機雙層隔振系統發生主共振時振動傳遞率的影響規律,如圖4-6所示。

圖3 輔機雙層隔振系統的理論解和數值解Fig.3 Theoretical and numerical solutions of vibration isolation system

圖4 C1對振動傳遞率的影響Fig.4 The effect of C1on the vibration transmissibility
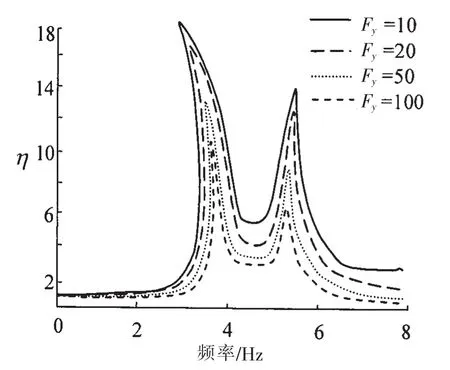
圖5 Fy對振動傳遞率的影響Fig.5 The effect of Fyon the vibration transmissibility
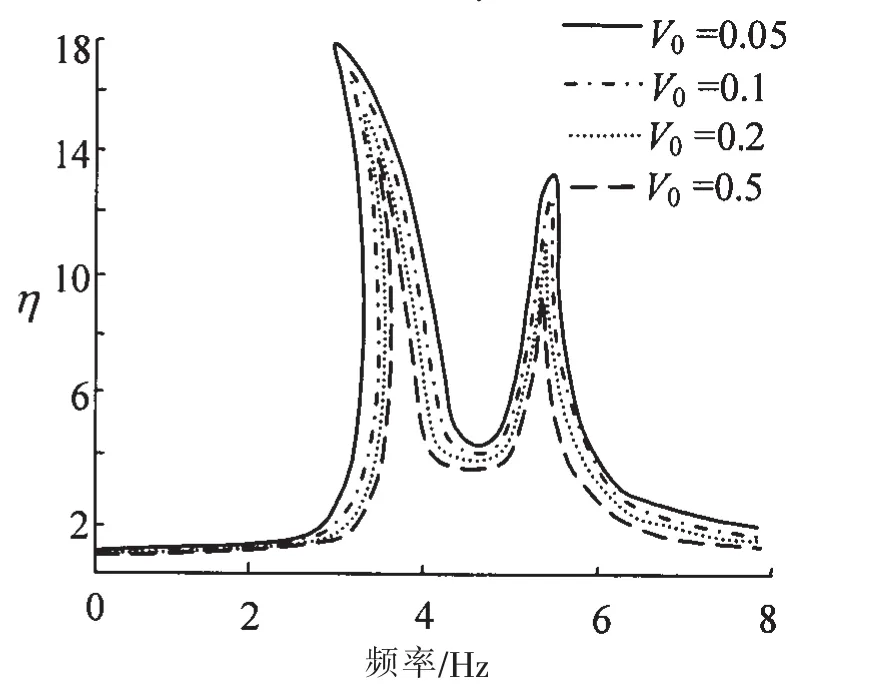
圖6 V0對振動傳遞率的影響Fig.6 The effect of V0on the vibration transmissibility
從這些圖中可以看出:當輔機激勵頻率接近3.6 Hz和5.2 Hz時,雙層隔振的系統發生主共振,系統的振動傳遞率急劇增加,系統的隔振效果被放大,磁流變阻尼器的各主要參數對其影響規律各自不同;輔機雙層半主動隔振系統的主共振具有典型的非線性特性;磁流變阻尼器的阻尼在主共振區域對半主動雙層隔振系統的振動傳遞率影響很明顯,雙層隔振系統的振動傳遞率隨著磁流變阻尼系數C1的增加而減小,在非共振區磁流變阻尼系數C1對系統響應的影響較小;磁流變阻尼器的控制力Fy在主共振區域對半主動雙層隔振系統的振動傳遞率影響明顯;磁流變阻尼器的零力速度V0由磁流變液的可壓縮性決定,對半主動雙層隔振系統的振動傳遞率影響不大,在低頻區和高頻區V0對振動傳遞率的響應影響都很小,控制力對振動傳遞率的影響沒有磁流變阻尼器的阻尼影響明顯。半主動隔振系統的幅頻響應振幅隨著控制力的增加而降低,半主動隔振系統變得更為穩定。
5 結 論
本文針對輔機雙層半主動隔振系統,利用平均法得到了系統振動的一次近似解,并與利用Maple得到的數值解進行了比較。結果說明理論解與數值解具有很好的一致性,可用于輔機雙層半主動非線性系統振動傳遞率特性的研究。
通過分析磁流變阻尼器主要參數對輔機雙層半主動隔振系統振動傳遞率影響發現:增加磁流變液的阻尼系數C1、零力速度V0和控制力Fy都能降低主共振時系統的振動傳遞率;磁流變液的阻尼系數C1和控制力Fy對振動傳遞率的影響比磁流變阻尼器的零力速度V0影響明顯。因此,在實際工程應用中可以通過增加磁流變阻尼器的阻尼系數C1和控制力Fy降低發生主共振時半主動雙層隔振系統的振動傳遞率,從而降低輔機振動傳遞到基座的力。

