Huber-based濾波在非合作航天器相對導航中的應用

施常勇 王 向

1. 上海航天控制技術研究所，上海 201109 2. 上海市空間智能控制技術重點實驗室，上海 201109

非合作航天器相對導航是完成在軌服務的前提，主要航天大國均開展了相關研究。在對非合作航天器的測量過程中，測量設備的誤差通常較大，角閃爍、目標機動等一些不確定因素也會對測量產生影響，為提高相對控制的精度，一般引入濾波處理。

目前，擴展卡爾曼濾波(EKF)是研究相對導航問題的主要手段，文獻[1]和[2]均采用EKF作為導航濾波器，且在文中假設噪聲輸入為嚴格的高斯過程，然而實際問題常常不滿足這一條件，嚴重時會導致濾波發(fā)散。對于存在非高斯噪聲輸入的系統(tǒng)，通常采用的濾波方法有UKF濾波[3]、H∞濾波[4]、L2/L∞濾波和L1濾波[5]等。1964年Huber 提出了廣義極大似然估計，即M估計，并提出一種用于解決在Gaussian分布附近存在一定對稱干擾的隨機量(即混合高斯分布)問題的實用方法，即Huber方法[6]。該方法結合l1/l2兩種范數構建代價函數，對于干擾為高斯分布的情形，可以使最大漸進估計方差達到最小；其魯棒性優(yōu)于基于l2范數的估計方法，盡量保持了純高斯分布時l2范數的估計效率，同時結合Kalman濾波的優(yōu)點，形成了Huber-based濾波(HBF)，該濾波器通過結合l1和l2范數估計器的特點，在處理對于量測噪聲為受污染的高斯白噪聲時具有較強的魯棒性，能夠很好地實現系統(tǒng)的狀態(tài)估計。

本文將HBF應用于非合作航天器相對導航中。仿真研究針對輸出噪聲為高斯和混合高斯分布的情況，考慮目標存在機動過程，對比了HBF濾波與EKF濾波的性能。具體安排如下：第1節(jié)，簡要介紹HBF算法；第2節(jié)，給出相對導航系統(tǒng)模型；第3節(jié)，針對不同工況進行數學仿真校驗；第4節(jié)，對全文進行總結。

1 Huber-based濾波器

設系統(tǒng)方程為：

(1)

其中，x和z分別為狀態(tài)值和量測量;ω和ν分別為系統(tǒng)模型誤差和測量噪聲。

1.1 狀態(tài)預測

(2)

(3)

(4)

Fk=?f(x,u,ω)/?x|x=xk

(5)

其中,Φk/k-1為離散系統(tǒng)一步轉移矩陣;T為濾波周期;xk+1|k和Pk+1|k為預測狀態(tài)估計值和狀態(tài)估計誤差協(xié)方差陣。

1.2 測量更新

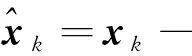
(6)

系統(tǒng)測量矩陣離散化后可寫成如下形式：

(7)

定義如下變量：

則：

yk=Mkxk+ξk

(8)

求解式(8)可采用線性回歸近似的Huber方法，定義代價函數ρ(·)，取其最小值， Huber代價函數定義如下：

(9)

(10)

(11)

求解上式可通過迭代解法：

(12)

(13)

Huber定義了一種代價函數的形式：

(14)

γ為調節(jié)參數，這種代價函數結合了l1，l2范數的性質，具有較好的魯棒性，其中γ在1～2 之間取值，一般選擇調節(jié)因子為1.345[7-8]，Huber已證明，當ρ(·)函數選擇式( 14) 的形式，選取該調節(jié)因子，HBF對受污染的高斯分布具有漸近最優(yōu)魯棒性。

狀態(tài)估計誤差協(xié)方差陣為

(15)

Xk+1=Xk+Ek

(16)

(17)

式中，Λ為待求矩陣。

2 相對導航系統(tǒng)設計

相對導航中，兩航天器的關系如圖1所示。

圖1 相對導航坐標系

設跟蹤航天器相對J2000慣性系的位置矢量為ro；目標航天器相對J2000慣性系的位置矢量為rt；目標航天器相對跟蹤航天器的位置矢量為ρ。

1)相對運動方程[12]

(18)

其中，n為跟蹤航天器軌道角速度；fx，fy和fz為軌道調整或變軌過程中控制力引起的加速度，可以通過加速度計測量得到；ωx，ωy和ωz為干擾加速度，主要由方程推導過程中的近似處理以及各種攝動加速度引起，用白噪聲近似。將式(18)寫成矩陣形式為：

(19)

2)相對測量設備測量量定義

相對導航常用的測量設備有微波雷達和激光雷達、光學相機與激光組合測量系統(tǒng)等，輸出形式如圖2所示。

圖2 相對測量設備輸出定義

ρ為目標星相對于追蹤星的視線距離；

臨床教學重視理論、實踐相結合，教學目的是培養(yǎng)學生獨立思考和解決問題的能力，學習疾病基礎知識。因婦產科學實踐性和理論性較強，婦產科患者疾病涉及隱私部位，患者自我保護意識較強，普遍存在讓抗拒帶教學生進行檢查現象，加大治療難度[7]。傳統(tǒng)教學模式學生學習主動性下降，重復學習情況嚴重，學生探究性不強；老師教授什么知識就學什么，學習較為隨意，沒有意識到婦產科學學習的重要性；傳統(tǒng)教學模式也是以老師為主的“填鴨式”教學，老師為主導，學生被動學習，獨立學習意識和思考意識缺乏。該種教學方式培養(yǎng)出的醫(yī)師已經不能適應多變的臨床情況和復雜的醫(yī)療環(huán)境，可能出現診斷失誤或其他醫(yī)療事故，嚴重威脅患者安全[8]。

α為目標星在追蹤星相對導航敏感器測量坐標系中的方位角，定義為目標星相對追蹤星視線在測量系XY平面的投影與X軸之間的夾角，偏向+Y軸方向為正；

β為目標星在追蹤星相對導航敏感器測量坐標系中的高低角，定義為目標星相對追蹤星視線與其在測量系XY平面投影之間的夾角，偏向-Z軸方向為正。

具體定義為：

3)量測與量測方程

(20)

其中：

相對導航量測方程為：

Z=HX+DV

(21)

間接測量的量測噪聲方差矩陣為：

E(DV, (DV)T)=D·E(V,VT)·DT=DRDT

(22)

3 仿真校驗

為校驗HBF在相對導航系統(tǒng)的可用性和適應性，采用高精度軌道動力學仿真2顆航天器的空間飛行軌跡，敏感器的誤差設置如表1，對高斯分布型噪聲、混合高斯噪聲及目標機動等3種工況，分別采用HBF和EKF進行仿真校驗。

相對導航周期：T=0.4s。

表1 敏感器誤差參數設置值(3σ)

3.1 正常誤差工況

采用表1中設置的敏感器誤差參數，HBF和EKF仿真曲線如圖3～4所示，從圖中可以看出，HBF相對EKF處理誤差小，且較平滑，其中HBF導航精度為2.03m，速度精度0.04m/s，而EKF相對導航位置精度為3.59m，相對速度精度為0.11m/s。

圖3 三軸相對位置估計誤差

圖4 三軸相對速度估計誤差

3.2 混合高斯噪聲模型工況

為檢驗HBF和EKF在混合高斯模型下的仿真性能，相對測量設備的誤差采用混合高斯噪聲模型，其表達式[15]為：

f(υk)=(1-ε)N(0,σ1)+εN(0,σ2)

(23)

仿真時，ε取0.6，σ2=2σ1，由表2可見，無論是高斯還是混合高斯分布情況下，HBF均表現出較好的導航性能：

表2 各算法運行結果

3.3 目標機動工況

采用表1參數，在t=500s時，目標星以0.1m/s的速度遠離跟蹤星(x向)，則兩型濾波器的濾波誤差曲線如圖5～6所示：

圖5 三軸相對位置估計誤差(目標機動)

圖6 三軸相對速度估計誤差(目標機動)

從圖中可以看出，EKF比較快速地敏感到速度的增加，而HBF則有一定的延遲，但HBF相對較平滑地實現了位置和速度的濾波估計，且最終精度依舊比EKF高。

4 結論

針對傳統(tǒng)Kaman濾波在輸入噪聲為非高斯噪聲時導航精度下降、甚至發(fā)散的問題，研究了Huber-based濾波器在空間非合作航天器相對導航系統(tǒng)中的應用技術，采用間接濾波方法，搭建仿真模型，對所設計的相對導航系統(tǒng)進行了仿真校驗，并將其與EKF進行對比分析。仿真表明，HBF性能較EKF優(yōu)，且具有較好的魯棒性和穩(wěn)定性，具有較強的工程應用價值。