臨近空間飛行器兩種捷聯慣導算法的等價性*

陳 凱 殷 娜 劉明鑫

西北工業大學航天學院，西安710072

臨近空間通常是指距地面20km～100km處的空域，臨近空間區域包括大氣平流層的大部分區域、中間大氣層區域和部分電離層區域。臨近空間下面的空域是傳統航空器的主要活動空間，其上面的空域是傳統航天器的運行空間。顧名思義，臨近空間飛行器是指高于普通飛行器飛行空間，而低于軌道飛行器運行空間區域的飛行器，臨近空間飛行器在臨近空間巡航飛行[1]。

本文探討臨近空間飛行器捷聯慣導算法。以助推-滑翔高超聲速飛行器為例，臨近空間飛行器的飛行剖面主要包括助推段、自由彈道段、彈道再入段、彈道爬升段和滑翔段等飛行階段[2]。從飛行階段看，助推段、自由彈道段、彈道再入段和彈道爬升段等階段，屬于航天領域的飛行軌跡，控制系統需要航天體系下的導航數據進行制導控制；而滑翔段飛行器沿著地球表面飛行，以地球表面作為參考，屬于航空領域的飛行軌跡，控制系統需要航空體系下導航數據進行制導控制。可見，高超聲速飛行器具有航天和航空的雙重飛行控制和導航需求。

一般認為，航天和航空2個領域的捷聯慣導算法，是為適應各自領域的應用而設計，二者互不相關。張衛東研究了航天體系下運載火箭的捷聯慣導算法[3]，航天體系下飛行器的典型特點是垂直發射，典型的飛行彈道是在射面附近。熊智針對高超、空天飛行器在發射過程中需要直接獲得發射慣性系下的高精度導航參數的需求，研究了發射慣性系下彈載組合導航系統[4]。Savage研究的捷聯慣導算法適合于航空體系下水平飛行的飛行器[5]。X-43A高超聲速飛行器采用的Honeywell公司的H-764系列INS/GPS組合導航系統，X-43A的飛控計算機與SLAM-ER防區外導彈相同，采用了航空體系下的導航算法[6]。X-51A和HTV-2均采用成熟的慣導系統[7-8]。Stephen S研究了地心慣性坐標系下高超聲速飛行器的捷聯慣導算法[9]。

針對不同的臨近空間飛行器，各種文獻采用了不同的導航算法，沒有相關文獻介紹各種體系下導航算法的相互關系。本文分別介紹了航天體系下發射慣性坐標系和航空體系下當地水平坐標系的捷聯慣導算法，推導了2種體系下導航信息的關系，為臨近空間飛行器捷聯慣導算法的選擇提供參考依據。

1 發射慣性坐標系導航算法

發射慣性坐標系下捷聯慣導算法是航天體系下的經典導航算法，輸出發慣系下適合垂直發射/起飛的飛行器的位置、速度和姿態信息。涉及的坐標系和定義如下[10-12]：

1)地心慣性坐標系(i系)；

2)地球固連坐標系(e系)；

3)發射坐標系(g系)；

4)發射慣性坐標系(a系)。發慣系是航天飛行器的導航參考坐標系;

5)彈體坐標系(ba系)，采用前上右坐標指向。

發慣系下的捷聯慣性導航方程如式(1)所示[3,13]。

(1)

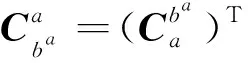
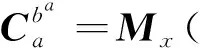
(2)

其中，φa為發慣系下飛行器的俯仰角；ψa為偏航角；γa為滾轉角；Mx(γa)、My(ψa)和Mz(φa)定義與文獻[12]相同。

2 當地水平坐標系導航算法

當地水平坐標系下捷聯慣導算法是航空體系下的經典導航算法，適合水平或傾斜發射/起飛的飛行器。其導航信息包括經緯高位置、相對當地水平的速度及相對當地水平的姿態角等當地水平坐標系下導航信息。航空體系下涉及的坐標系和定義如下[10-12]：

1)當地東北天水平坐標系(水平系，n系)，當地水平系是航空飛行器的導航參考坐標系。

2)彈體坐標系(bn系)，本文采用右前上坐標指向。

當地水平系下的捷聯慣性導航方程為如式(3)所示[5]。

(3)

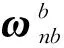
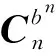
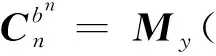
(4)

臨近空間飛行器的巡航飛行高度大于傳統航空飛行器的飛行高度。基于當地水平坐標系的重力公式采用簡化球形模型，對于臨近空間飛行器長時間長距離飛行會帶來較大誤差[13]。本文采用地固系下的J2重力模型，計算方法如式(5)所示。

(5)

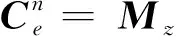
(6)

ge=Ge+ωie×ωie×re

(7)

(8)

(9)

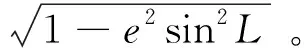
3 2種體系下導航信息的等價性

根據航空體系水平系下的位置、速度和姿態導航信息，可推導出航天體系下發慣系下的導航信息，由此證明，發慣系下的導航信息和水平系下的導航信息是等價的。

3.1 位置信息的等價性

當已知飛行器當前的緯經高(L,λ,H)時，可根據式(9)得到地固系下的位置pe，再根據pe可得到發射系下的當前位置pg為

(10)

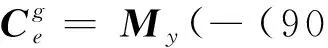
(11)

發射系與發慣系的區別在于：發慣系是不隨地球自轉的，而發射系是與地球固連隨著地球自轉的。因此，假設地球不旋轉，所以此時發慣系下的經緯高(L1,λ1,H1)如式(12)所示。

(12)

(13)

可得發慣系下的位置pa。

(14)

3.2 姿態信息的等價性

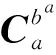
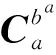
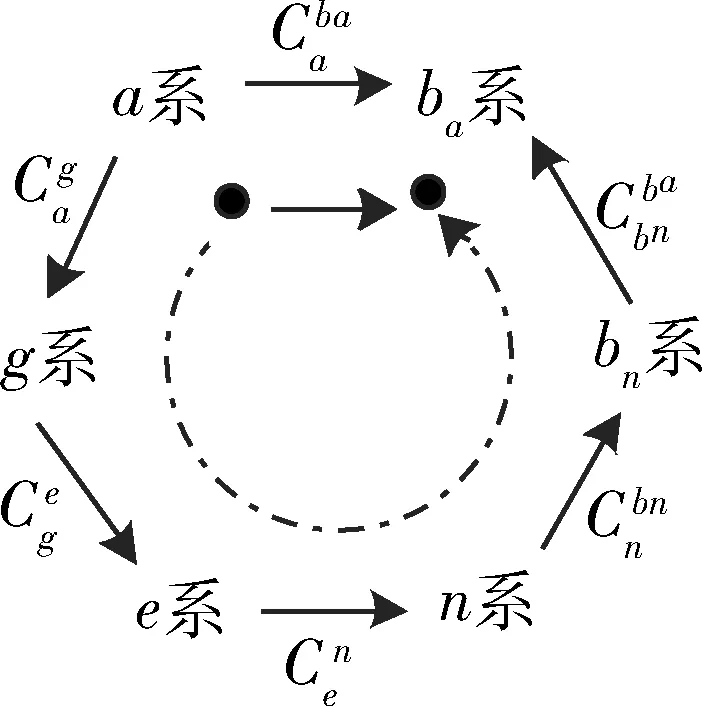
圖1 姿態矩陣傳遞關系

(15)

式(15)中，各姿態矩陣的定義為：

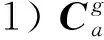
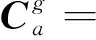
(16)

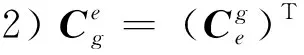
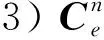
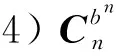
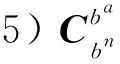
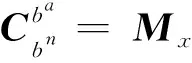
(17)

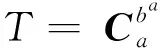
(18)

3.3 速度信息的等價性

根據水平系下的速度矢量vn，可得到發射系下的速度矢量vg

(19)

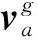
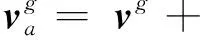
(20)

其中，pg如式(10)所示，則發慣系下速度va為

(21)

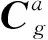
4 結論

針對臨近空間飛行器具有航天和航空雙重導航信息需求的特點，介紹了航天體系下發射慣性坐標系捷聯慣導算法和航空體系下當地水平坐標系的捷聯慣導算法，推導了2種體系下導航信息的等價性。可根據實際的臨近空間飛行器飛行彈道特點，選擇合適的導航體系。