基于觀測器的線性離散信息融合預見控制算法

高春雷 趙 賓,2 胡 洲

1.南京航空航天大學金城學院，南京211156 2. 南京航空航天大學自動化學院，南京211106 3. 四川航天系統工程研究所，成都 610100

最優控制的二次型性能指標函數中通常包含期望軌跡和控制能量的軟約束信息，信息融合預見控制算法通過融合這些軟約束信息以及系統狀態方程和輸出方程的硬約束信息，獲得協狀態和控制量的最優估計。文獻[1～5]利用信息融合估計方法求解線性系統和非線性系統的最優控制問題。文獻[6]針對期望軌跡和干擾可預見的最優跟蹤問題，提出了一種基于誤差系統的信息融合最優控制方法。文獻[7]設計了欠驅動垂直起降飛行器懸停模式下的非線性信息融合控制方法，具有良好的控制效果和解耦性能。

信息融合控制算法本質上是一種基于狀態反饋的最優控制方法，在利用該算法構建控制系統時需要引入全狀態反饋。但在實際工程中，如吊車控制系統[8]、水面船舶控制系統[9]等的部分狀態變量無法直接測量得到，導致以上方法在實際應用中都存在不同程度的局限性。針對這一問題，本文提出了基于觀測器的線性離散信息融合預見控制算法，證明了在該算法中運用觀測器設計狀態反饋仍然具有分離特性。

1 線性非時變離散系統的可控可觀性

線性非時變離散系統的狀態方程式為：

x(k+1)=Ax(k)+Bu(k)

(1)

y(k)=Cx(k)+Du(k)

(2)

考慮狀態反饋：u(k)=-Kx(k)+v(k)，則在此反饋作用下，閉環系統為：

x(k+1)=(A-BK)x(k)+Bv(k)

(3)

針對系統(1)、(2)構造系統的觀測器，即：

(4)

式中，x(k)是系統的n維狀態；u(k)是m維輸入；y(k)是實際系統的p維輸出，k為離散時間；A,B,C,D為適當維度的常數矩陣；x(0)為系統初始狀態，x(0)=x0。

引理1 對于式(1)和(2)所組成的線性非時變離散系統，若A為非奇異，則此系統用狀態反饋(3)時能任意配置極點的充要條件是(A,B)能控，即rankU=rank[B,AB,…,An-1B]=n。如果A為奇異，則此僅為能控的充分條件[10]。

引理2 對于系統(1)和(2)，若A為非奇異，狀態觀測器(4)存在的充要條件是(A,C)能觀，即rankU=rank[C,ATCT,…,(An-1)TCT]T=n。如果A為奇異，則此僅為能觀的充分條件[10]。

2 線性離散信息融合預見控制算法

對于系統(1)和(2)，假設y*(k)表示p維期望輸出向量。提出如下控制問題：求取某一控制律,使系統實際輸出y(k)跟蹤期望輸出y*(k)，并使得性能指標函數

(5)

取值最小。式中，信息權重矩陣Q(k+1)∈Rp×p，R(k)∈Rm×m為對稱正定陣[6]。控制量u(k)的最優融合估計為：

(6)

(7)

(8)

帶觀測器的信息融合預見控制系統框圖如圖1。

圖1 帶觀測器的信息融合預見控制系統框圖

3 狀態觀測器設計

假設系統(1)和(2)可觀，構造觀測器：

(9)

選擇“反饋增益矩陣”G，使(4)穩定，即使A-GC的特征根全部在單位圓內。由此可得：

(10)

由于A-GC的特征根全部在單位圓內，所以式(5)穩定，即有：

(11)

(12)

對于連續系統配置極點，極點越往左方遠離虛軸，則系統越穩定，回到平衡位置的速度也越快。而對于離散系統，需要將極點配置在單位圓內，極點越靠近原點越穩定。通常將離散系統的所有極點直接配置在原點，以使所有狀態估計值達到最快的收斂速度。

e(z)=zn+an-1zn-1+…+a1z+a0

(13)

由式(6)容易看出，該控制量的求取表達式是一個關于x(k)的全狀態閉環反饋控制系統，由于本文所討論的是基于觀測器設計閉環反饋控制系統，則式(6)可變為

(14)

(15)

其中，y(k)為系統的輸出信息，在實際系統中，即為傳感器的量測信息。

4 分離特性證明

定理1 對于形如式(1)和(2)所表示線性離散信息融合預見控制系統，構造如式(4)所示的觀測器，分離特性仍然成立。對于如式(6)所示的閉環狀態反饋控制系統，其反饋狀態由觀測器估計狀態替代后，仍然保留系統原有的性質。

證 由式(6)可表示為

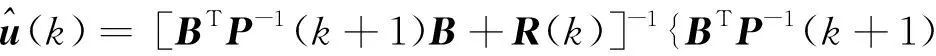
可得：

(16)

又由

y(k)=Cx(k)

(17)

將式(16)和(17)代入式(15)中，可得：

(18)

將式(16)代入式(1)中，可得：

(19)

結合式(18)和(19)，可得到增廣系統方程如下：

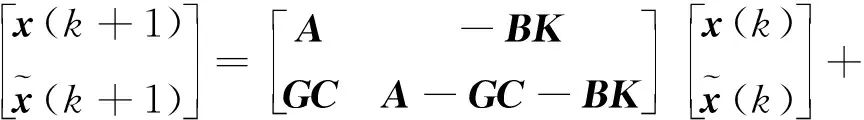
(20)

(21)

式(21)表明，整個系統的特征多項式分別由(A-BK)和(A-GC)的特征多項式的乘積構成。因此，觀測器的引入不影響由信息融合預見控制算法所配置的狀態反饋系統的特征值λ(A-BK)，而狀態反饋也不影響觀測器的特征值λ(A-GC)。由此可以得出，連續線性系統具有的分離特性，在線性離散信息融合預見控制系統中同樣成立。證畢。

5 仿真實驗

為了驗證在信息融合控制中運用觀測器的有效性，本小節通過吊車這一實際系統進行仿真實驗。為了避免被控對象過于復雜，下面考慮一個典型的一維吊車系統的“擺動抑制控制問題”。根據文獻[8,11]，一維吊車系統的線性化動力學模型表示如下：

輸出方程中包含小車的運動位置和負載的擺角，構造輸出方程如下：

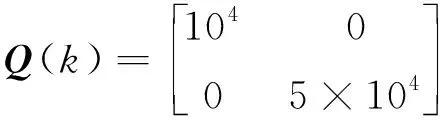
假設觀測方程即為輸出方程，小車的運動位置和負載擺角可直接測量。系統完全可觀測，即：rankU=rank[C,ATCT,…,(A4-1)TCT]T=4，則存在：

使得A-GC的特征多項式(式13)為zn，代入A、C及相關的參數后求得：

為了清楚展現估計狀態的收斂過程，圖2～圖5的仿真時間取為2s。從上面的4個圖中可以看出，雖然仿真前僅假設了x2和x4的觀測值包含初始誤差，但在實際估計過程中，x1和x3的觀測值也包含了誤差。這是因為本文所采用的仿真模型是一個欠驅動系統，系統的各個狀態間存在嚴重耦合，所以導致在估計的過程中x1和x3的觀測值與真實值也會有所偏差，不過，這4個狀態的觀測誤差在經過4步估計后就收斂到0了。

圖2 吊車位置估計誤差

圖3 吊車速度估計誤差

圖4 負載擺動角度估計誤差

圖5 負載擺動角速度估計誤差

圖6為吊車系統的小車位置跟蹤和負載擺角跟蹤誤差曲線，由仿真結果可以看出在負載吊運過程中，吊車系統在5s左右同時實現了小車位置跟蹤和擺角抑制。本文所采用的仿真對象模型及參數與文獻[8]基本相同，文獻[8]采用了部分反饋線性化方法，最后的仿真結果是吊車系統在7s左右同時實現了小車位置的跟蹤和負載擺動的抑制。通過對比可以發現，本文所采用的方法具有更好的控制效果。

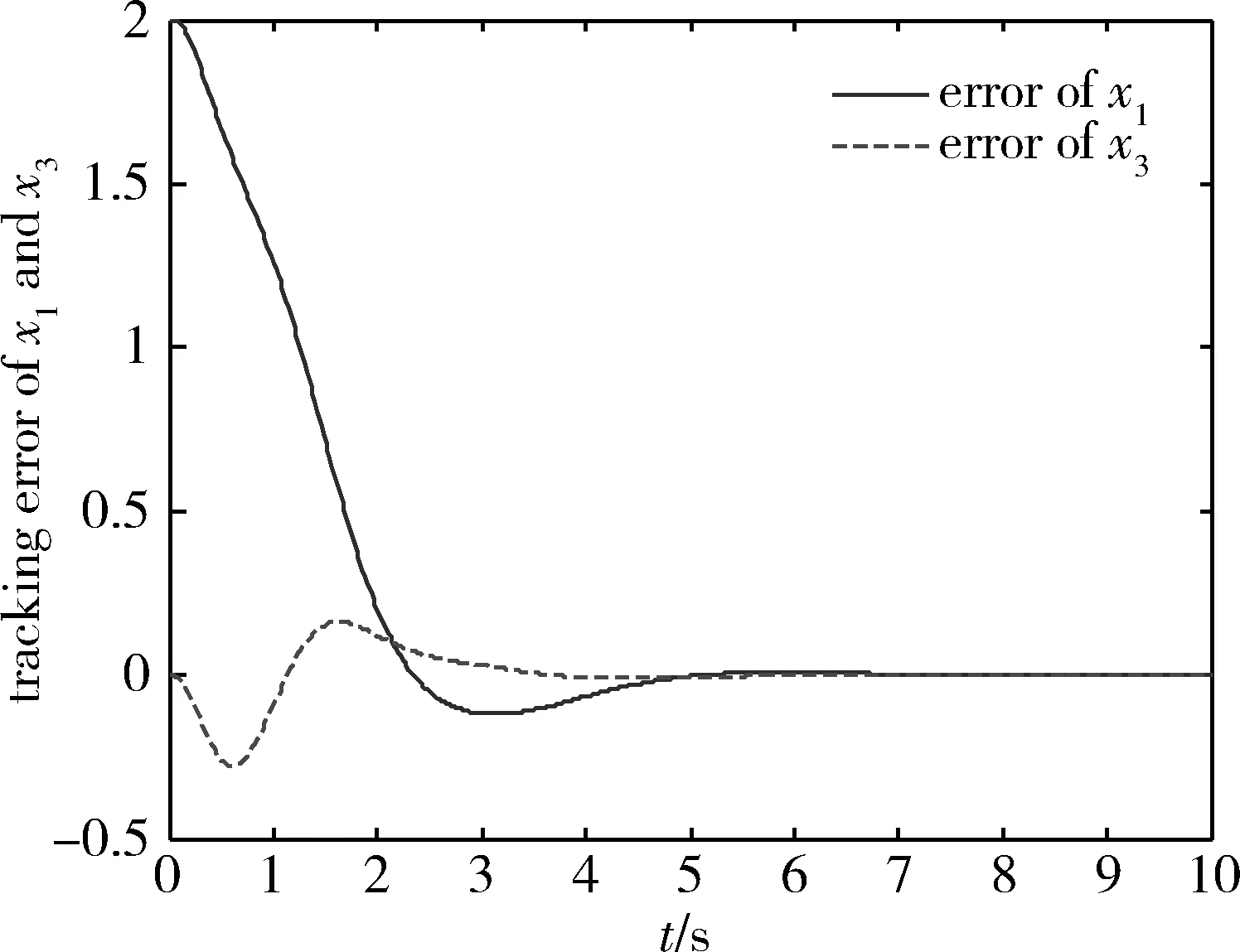
圖6 小車位置和負載擺角的跟蹤誤差

6 結論

針對線性離散信息融合預見控制算法在實際應用中難以實現全狀態反饋的問題，提出了一種基于離散觀測器構建其全狀態反饋的方法，并證明了對于利用觀測器設計的線性離散信息融合預見反饋控制系統，分離特性仍然成立，在觀測器的估計初值有誤差的情況下，最多經過n步估計(n為系統的狀態維數)，觀測誤差就可以收斂到0。