考慮天氣狀態的接觸網可靠性評估方法研究
王 貞,林 圣,馮 玎,高仕斌,陳 靜
(1.西南交通大學 電氣工程學院,四川 成都 610031;2.國網山東省電力公司 萊蕪供電公司,山東 萊蕪 271100;3.中鐵第一勘察設計院集團有限公司,陜西 西安 710043)
高速鐵路牽引供電系統要求具有極高的運行可靠性[1-3],無備用接觸網系統是牽引供電系統的關鍵組成部分,其能否安全可靠地進行服役直接關系到機車的安全、穩定運營。因此,如何更加準確評估接觸網的可靠性并使之提高,成為提高整個高速鐵路可靠性的關鍵[4]。
接觸網系統由完全暴露于室外的元件組成,受外部天氣因素影響較大,其故障率與修復率具有隨機模糊的特性,不是恒定常數。但目前對于接觸網的可靠性評估基本都是基于元件恒定故障率來進行的,如文獻[5-7]在假定故障率與修復率為恒定常數的特殊條件下分別基于馬爾科夫、貝葉斯網絡以及GO-FLOW方法建立接觸網可靠性分析模型,對接觸網系統的可靠性進行評估。
目前,國內外對考慮接觸網可靠性受天氣影響的研究鮮有報道,但針對輸配電系統可靠性受天氣狀態影響的研究相對較多。文獻[8]在配電網可靠性評估中,提出了惡劣天氣嚴重程度和持續時間概率特性對故障率和修復時間影響的模型。文獻[9]給出了基于天氣因素的可靠性參數修正模型,計算結果驗證了天氣因素對配電網可靠性指標有較大影響。在此基礎上,文獻[10]利用聯系數理論處理故障率與天氣波動,提出了考慮天氣變化的輸電系統可靠性評估方法。以上研究在一定程度上考慮了天氣對可靠性參數或指標的影響,但未充分考慮故障率、修復率及天氣狀態的隨機模糊性。
文獻[11-12]運用可信性理論有效地解決了電力系統中數據的隨機模糊性問題,并在電力系統風險評估、電網規劃等方面得到了較好地應用。基于此,文獻[13]基于可信性理論對接觸網系統可靠性進行模糊評估,文中并沒有考慮天氣狀態對系統可靠性指標的影響。但在我國電氣化鐵路中,如蘭新線、武廣線等接觸網系統受大風、雷雨等惡劣天氣情況的影響較嚴重,其子系統元件故障率、修復率的隨機模糊性明顯。因此,在進行接觸網可靠性評估時有必要考慮天氣狀態對其評估結果的影響。
針對上述問題,本文提出一種考慮天氣狀態的高速鐵路接觸網系統可靠性評估方法,此方法依據IEEE標準導則[14]將天氣分為正常(Normal)天氣、惡劣(Adverse)天氣、災難(Storm Disaster)天氣,建立三態天氣可靠性評估數學模型,將周期內統計所得各類元件平均故障率、修復率以及各天氣狀態持續時間所占統計周期的比例作為原始參數,通過三態天氣模型求取不同天氣狀態下元件故障率、修復率,由于元件故障率、修復率以及天氣狀況均具有不確定性,故將其看作隨機模糊變量,運用可信性理論處理故障率、修復率以及天氣情況變化。通過GO法計算不同天氣狀態下接觸網系統可靠性指標。此方法能夠在原有數據基礎上得到不同天氣狀態下系統可靠性指標,減少了數據統計量,同時保留了原始數據的隨機模糊性,貼近現場實際。
1 考慮天氣狀態的元件參數模型
接觸網系統的全部設備均在戶外運行,特別是接觸線,受天氣的影響比較大,不同天氣狀態下元件故障率與修復率不同。災難天氣狀態下,大暴雨、暴雨等容易造成絕緣子的閃絡,暴風容易將接觸線、吊弦、承力索等吹斷,同時容易將異物吹到接觸網上導致短路跳閘,暴雪低溫容易使接觸線敷冰導致受電弓不能正常取流;惡劣天氣下,雷擊導致過電壓引起絕緣子損壞,同時過電壓侵入變電所導致跳閘[15];正常天氣下,鳥害鳥窩、施工等意外情況是引起接觸網故障的主要因素。不同天氣狀態下元件的故障率存在較大差異,災難天氣下元件發生故障的可能性明顯增加[16]。同時受工作環境的影響,災難天氣及惡劣天氣下設備修復率會低于統計周期內的平均修復率。為此本文建立三態天氣下元件的故障率及修復率修正模型,定量表征天氣狀態對接觸網故障率及修復率的影響。
1.1 三態天氣下元件故障率修復模型
將天氣分為正常(Normal)天氣、惡劣(Adverse)天氣、災難(Storm Disaster)天氣3個狀態,三態天氣的持續時間都是隨機的,采用期望值來描述。在一個統計周期內,三態天氣持續時間期望值與元件故障率關系如圖1所示。S表示災難天氣持續時間期望值,D表示惡劣天氣持續時間期望值,N表示正常天氣持續時間期望值,T表示統計周期。對應天氣狀態下故障率分別為λs、λd、λn。
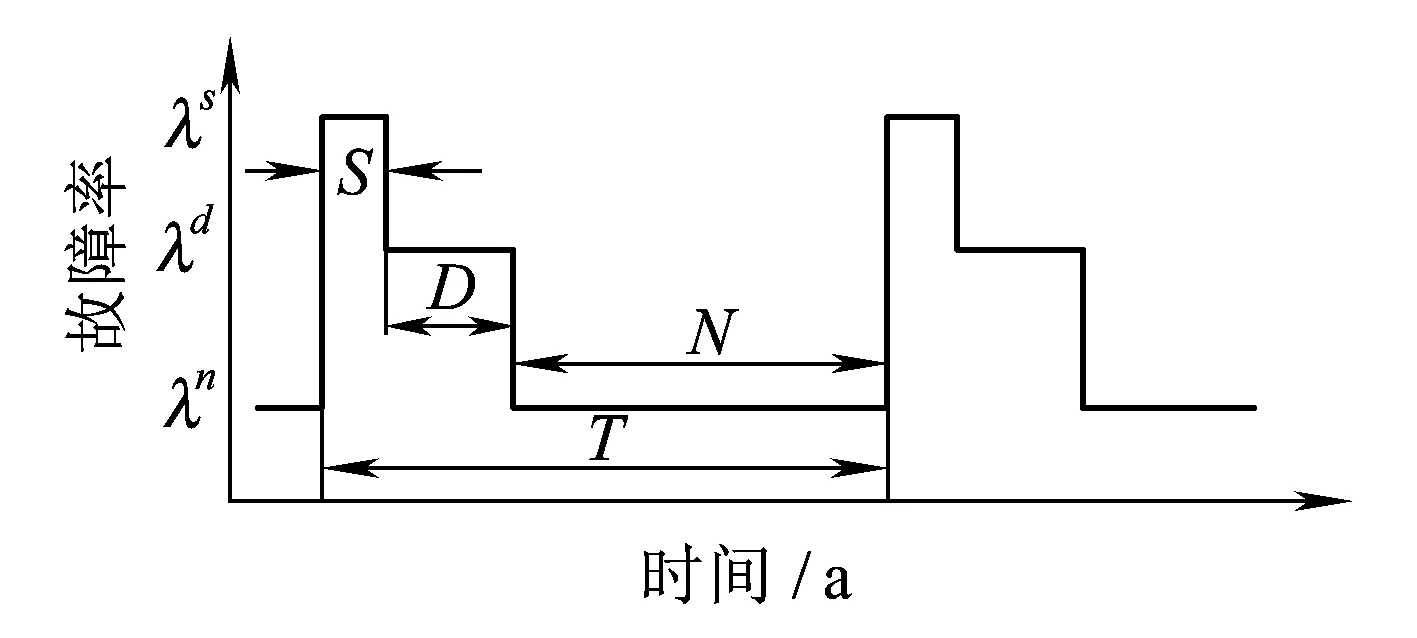
圖1 統計周期內三態天氣持續時間期望值
設某類元件平均故障率為λavg,在第j態天氣下元件故障率為λj,統計周期為T,元件在統計周期內發生故障的總次數為Nλ,第j態天氣持續時間期望值為Tj,第j態天氣下發生故障次數為Nj,則有
(1)
設Pj為第j態天氣持續時間占統計周期的百分比,則有
(2)
由式(1)、式(2)可得
λavg=∑Pjλjj=s,d,n
(3)
式(3)即為三狀態天氣模型下各類元件故障率的修正模型[8]。
設Fj表示某類元件在第j態天氣下發生故障次數占統計周期內總故障次數的百分比,則有
(4)
如何求得第j態天氣某元件故障率λj是評估接觸網系統不同天氣狀態下可靠性指標的關鍵,但現場實際中λj較難得到,而λavg的值相對容易統計,若知道某類元件在第j態天氣下發生的故障次數占統計周期內總故障次數的百分比Fj,則由式(3)、式(4)可推導出
(5)
對于某類元件在第j態天氣下發生故障次數占統計周期內總故障次數的百分比Fj是一個相對穩定值,通過多年統計結果可以將Fj看作是已知量,故只要統計得到第j態天氣持續時間占統計周期的百分比Pj,運用式(5)即可在統計所得各類元件平均故障率的基礎上求得三態天氣下各類元件的故障率。
1.2 三態天氣下元件修復率修正模型
平均修復時間是指可修復元件的平均修理時間,其估計值為修復時間總和與修復次數之比,在可修復系統中,平均修復時間倒數即為修復率[17]。設某類元件統計周期內平均修復時間為Tavg,災難天氣、惡劣天氣、正常天氣狀態下平均修復時間為ψs、ψd、ψn,對應的故障次數為Ns、Nd、Nn,則有
j=s,d,n
(6)
在現場實際中,3種天氣狀態下的平均修復時間也較難獲得,而Tavg的值卻較容易統計,因而同樣只要知道3種天氣狀態下某類元件平均修復時間的比值即可通過式(6)計算得到各類元件不同天氣狀態下的平均修復時間,從而求得修復率為
μj=1/ψjj=s,d,n
(7)
3種天氣狀態下某類元件平均修復時間的比值是一個相對穩定的值,通過多年的統計結果可以將其看作已知量,進而可在統計所得周期內各類元件平均修復時間基礎上通過式(6)、式(7)求得不同天氣狀態下某類元件修復率。
在上述公式中,λavg、Tavg、Pj、Fj的求取通常是用幾個日歷年統計結果的平均值,現場實際中,這些參數因統計誤差或者統計資料不足而具有不確定性。為了考慮這些不確定性因素對系統可靠性評估的影響,本文基于可信性理論進行不確定性建模。
2 基于可信性理論的不確定性建模
可信性理論將模糊論與概率論在測度的基礎上有機結合,適用于具有隨機性與模糊性系統的綜合評估,為隨機模糊雙重不確定性問題的求解工作提供了可能[18]。接觸網各類元件故障率、修復率以及天氣狀態具有模糊性與隨機性的特性,可信性理論能夠有效處理該特性。本文將三態天氣模型下所求故障率與修復率看作隨機模糊變量,滿足了其隨機性和模糊性的雙重特性,同時也反映出天氣狀態的不確定性,進而運用可信性理論求得接觸網系統不同天氣狀態下的可靠性指標。
具體做法是通過式(5)~式(7)計算得到某類元件在第j態天氣下的故障率λj、修復率μj,將計算所得λj、μj視為隨機模糊變量ξ、η,接觸網系統的可靠性指標計算轉換為運用可信性理論求解隨機模糊變量數學期望值的數學問題。下面給出與本文相關的幾個概念與計算式。
假設Θ為非空集合,P(Θ)為Θ的冪集,若Pos滿足可信性理論的四條公理[19],則稱Pos為可能性測度;(Θ,P(Θ),Pos)則為可能性空間;A為P(Θ)中的一個集合,Ac為A的對立集合,則Nec{A}=1-Pos{Ac}為A的必要性測度;Cr{A}=(Pos{A}+Nec{A})/2為A的可信性測度。
可信性測度與隸屬度函數之間有如下關系,對于隸屬度為g的模糊變量ξ,設B為P(Θ)中的集合,Bc為B的對立集合,有
(8)
如果隨機模糊變量ξ、η是從可能性空間(Θ,P(Θ),Pos)到隨機變量集合上的映射,則函數f關于變量ξ、η的期望值為
Epro-fuz[f(ξ,η)]=
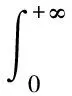
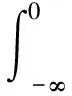
(9)
其中
Epro[f(ξ(θ),η(θ))]=
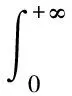
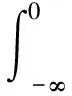
(10)

在處理系統的一般隨機模糊變量時,很難直接通過上式求得所需要結果,為此本文通過隨機模擬技術求取期望值,當N充分大時,對任意的r≥0,可信性測度Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))]≥r}可近似為
Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))]≥r}≈
(11)
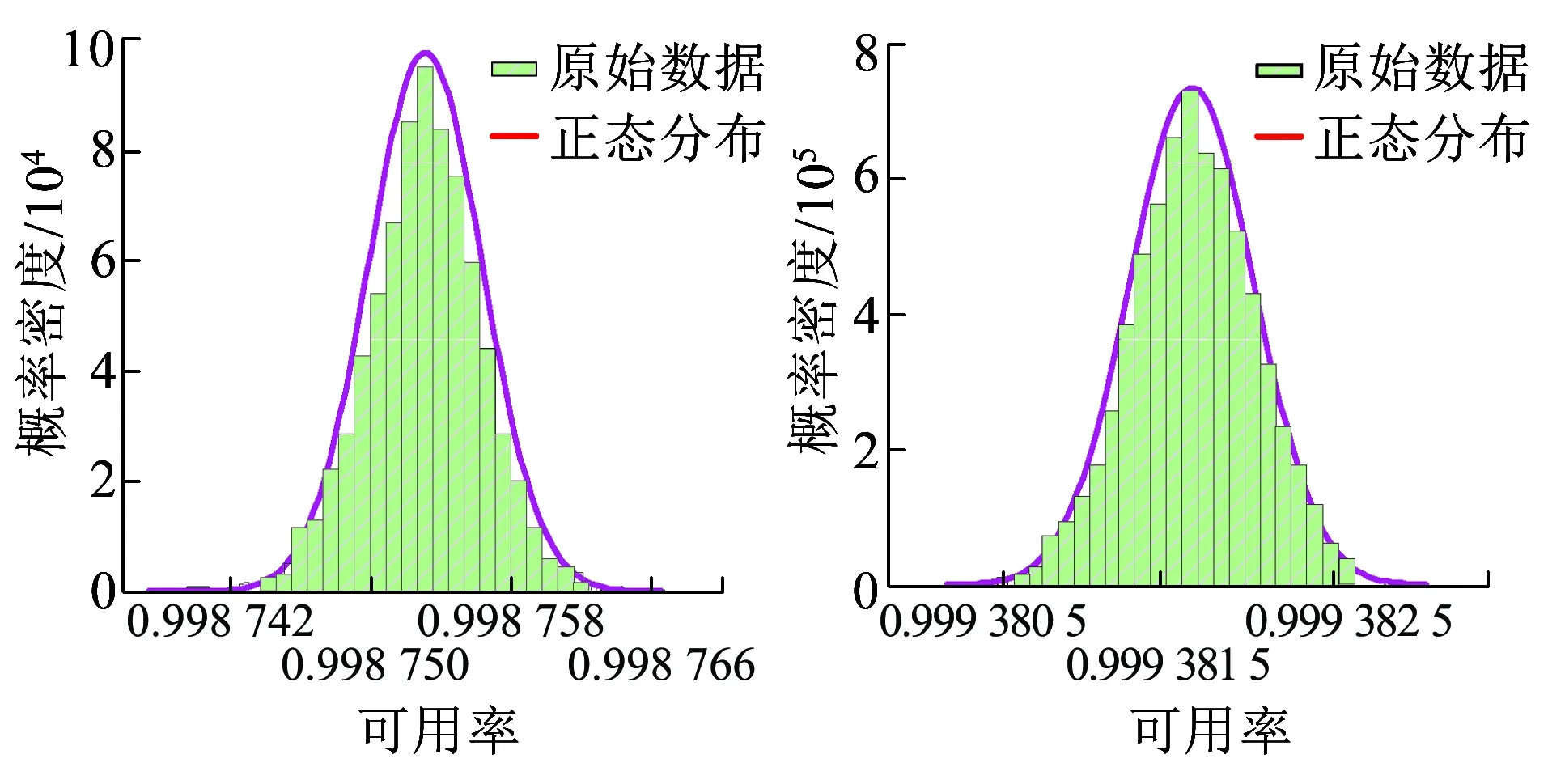
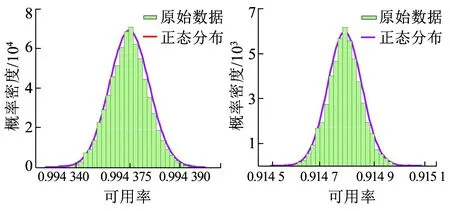
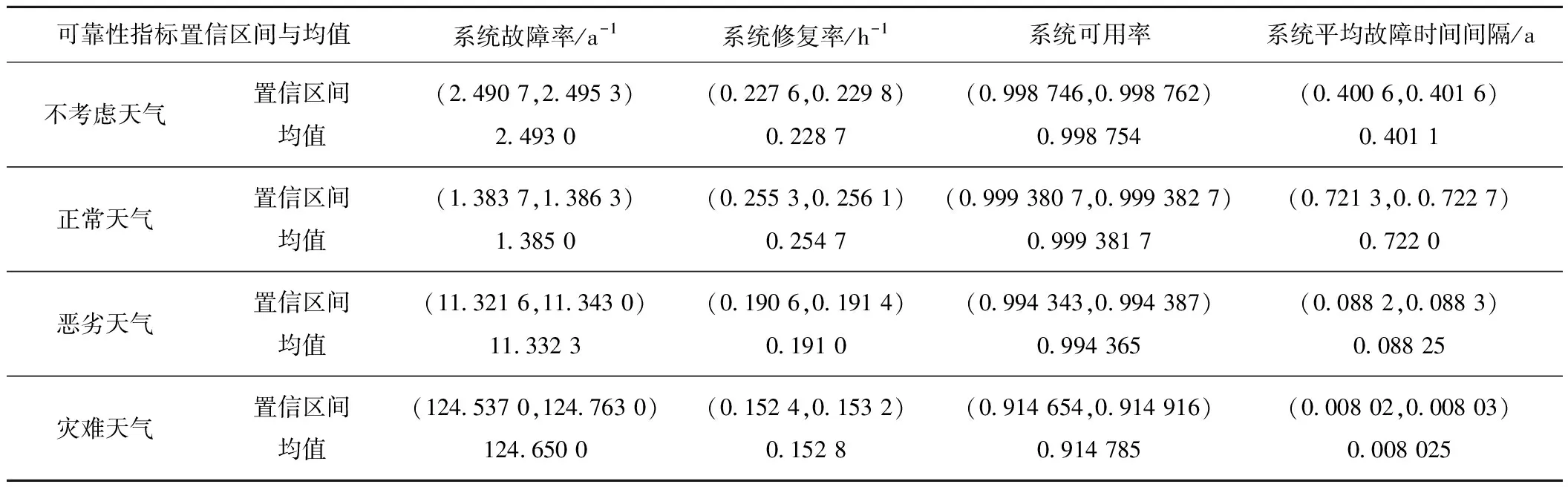
對任意的r<0可信性測度Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))] Cr{θ∈Θ|Epro[f(ξ(θ),η(θ))] (12) 其中,Epro[f(ξ(θk),η(θk))]可以通過隨機模糊模擬得到,則式(9)可由式(11)、式(12)兩式等價求得,隨機模糊變量的期望值Epro-fuz[f(ξ,η)]即可求得。 在系統可靠性和風險評估分析中,故障樹分析法是比較常用的一種方法,而GO法是另一種以成功為導向的系統可靠性分析方法,相比于故障樹有其自身特點[20]:一是GO法以成功為導向選擇相應的GO操作符直接將系統原理圖轉換為模型圖,GO圖中的操作符與系統中部件一一對應,能夠清晰地反映系統結構組成,明顯描述出相關部件之間的關系及相互作用,易于與原系統進行核對;二是通過GO運算計算元件各種狀態發生的概率,不需要最小割集,直接對系統定量分析,求解精度高。綜合分析,GO法能夠將接觸網系統失效模型直接轉換為GO圖進行可靠性評估,模型結構清晰,貼近現場實際,以信號流為成功導向計算簡單明了,因此本文選擇GO方法計算不同天氣狀態下系統可靠性指標。 只有當所有部件都正常工作時接觸網系統才能正常工作,接觸網系統失效時,可以等效看作是接觸線、承力索、絕緣子、吊弦、承力索座、水平拉桿、定位裝置、套管、線夾、定位環、斜腕臂、支柱基礎等失效部件的串聯系統,為分析方便,假設各類元件為一個單元。本文根據接觸網系統等效失效模型,以系統能正常工作為成功導向,依照GO法模型與邏輯框圖一一對應原則建立接觸網系統GO圖,為保證GO圖完整性,以操作符5(信號發生器)代替外部供電系統作為輸入信號,接觸網元件采用操作符1(兩狀態單元)代替,系統失效模型及GO圖如圖2所示。圖2中“5-0”指操作符為5,元件標號為0,輸出信號流“12”的輸出數據代表接觸網系統的可靠性指標。本文只針對接觸網系統進行可靠性評估,故假設操作符5的失效概率為0。 在圖2中給定各單元可靠性參數,即可根據GO運算計算出整個系統可靠性指標。實際工程中一般給出元件故障率和修復率兩個參數,據此可以計算輸出信號的故障率與修復率,進而可計算出整個系統的可用率。 (a)接觸網系統等效失效模型 (b)接觸網系統GO圖圖2 接觸網系統失效模型及GO圖 接觸網系統是一個具有停工相關的串聯可修復系統,即系統因某單元故障而停工時,沒有故障的單元隨系統停工而停止運行,且不再發生故障,直到系統修復,這些單元再恢復正常運行[21]。考慮到接觸網系統實際工況,認為整個系統各單元之間均存在停工相關且停工階數I=1。此時對于兩狀態單元,輸出信號計算公式為 (13) 式中:λC、μC為操作符本身故障率與修復率;λS、μS為輸入信號故障率與修復率;λR、μR為輸出信號故障率與修復率。 當多個單元存在一階停工相關時,串聯結構故障模式只是1個單元故障,沒有2個或者多個單元同時故障,由式(13)得串聯結構等效故障率為所有單元故障率之和;系統故障率和修復率比值,是所有單元故障率和修復率的比值之和[21],將故障率與修復率看作隨機模糊變量,得到三態天氣下系統等效的故障率、修復率、可用率、平均故障時間間隔公式為 (14) (15) (16) (17) 運用式(5)~式(7)計算求得不同天氣狀態下各單元故障率、修復率,通過式(14)~式(17)將接觸網系統可靠性評估問題轉換為隨機模糊變量數學期望求解問題,即可運用可信性理論實現接觸網系統的可靠性評估。由于算法求解過程用到隨機模糊模擬的方法,因此求解結果存在一定隨機性,重復求解M次,分析結果分布規律,給出置信區間,具體算法流程如圖3所示,圖3中N指隨機產生N個r,算例中M、N均取1 000。 圖3 三態天氣下可靠性指標計算流程 本文采用文獻[13]寶成鐵路的統計數據,以100 km長的接觸網為統計基準,對每個部件的失效和維修情況進行記錄,得到各部件不考慮天氣狀態時元件的平均故障率與修復率,見表1,以此為原始數據。假設通過對幾個日歷年的數據分析得出正常天氣、惡劣天氣、災難天氣持續時間占統計周期百分比均值Pj分別為90%、9.9%、0.1%,假設故障發生在正常天氣、惡劣天氣、災難天氣下的次數占總故障次數的百分比Fj分別為50%、45%、5%[8],并且假設在正常天氣、惡劣天氣、災難天氣時元件的修復率之比為6∶5∶4。 表1 接觸網各元件故障率與修復率 基于可信性理論,隨機模糊變量的模糊性可以用各種形式的模糊定義來表達,通常所用表示形式有三角形模糊數及梯形模糊數。本文為研究模糊數表示形式對可靠性計算結果的影響,以系統故障率為例,分別用三角形模糊數以及梯形模糊數來描述各元件故障率的模糊分布,以表1中故障率的±2%誤差作為模糊分布上下限,0.2%誤差作為可能性最大值,通過圖3所示流程圖以及式(14)計算系統故障率,重復計算1 000次,對計算結果擬合求得95%置信區間及均值,見表2。 表2 不同模糊變量表示形式下系統的故障率 a-1 由表2可知,用三角形模糊數表示各元件故障率時求得系統故障率均值為2.493 0 a-1,用梯形模糊數表示各元件故障率時求得系統故障率均值為2.491 9 a-1。表明不同模糊表示形式對所求系統可靠性指標結果幾乎沒有影響,本文在后文算例中選擇三角形模糊數來表示各元件的故障率與修復率。 在實際計算中模糊區間難以給出具體定義,為研究模糊區間范圍對可靠性結果的影響,以求取系統故障率為例,用三角形模糊數表示表1中各元件故障率,以故障率的±α誤差作為模糊分布上下限,0.2%誤差作為可能性最大值,選取不同的α值,通過圖3所示流程圖以及式(14)計算α值不同時系統的故障率,計算結果如圖4所示。 圖4 不同模糊區間范圍的計算結果 由圖4可知,不同模糊區間上下限對計算結果有一定影響,區間范圍越大,計算結果越小。因而,為考慮線路實際服役環境的天氣變化情況,計算時可將統計周期內幾個日歷年中λavg、μavg的最大值作為模糊區間上限,最小值作為下限,均值作為可能性最大值。由于本文統計數據有限,故在后文計算中選擇故障率與修復率的±2%誤差作為模糊區間上下限,0.2%誤差作為可能性最大值。 運用式(5)~式(7)及表1數據,計算得到不同天氣狀態下各元件的故障率與修復率,見表3。 表3 三態天氣下各元件的故障率與修復率 將計算所得三態天氣下接觸網系統各元件的故障率以及修復率均視為隨機模糊變量,以±2%誤差作為模糊分布上下限,0.2%誤差作為可能性最大值,通過圖3所示流程及式(14)~式(17)可得接觸網系統三態天氣下可靠性指標的評估結果。由于在計算過程中用到了隨機模擬算法,重復計算1 000次,對不同天氣狀態下接觸網系統可靠性指標計算結果進行擬合,系統可用率擬合結果如圖5所示。圖5中橫坐標表示系統可用率,原始數據指經過1 000次計算得到的系統可用率樣本,擬合結果屬于正態分布。 (a)不考慮天氣時系統可用率 (b)正常天氣時系統可用率 (c)惡劣天氣時系統可用率 (d)災難天氣時系統可用率圖5 系統可用率擬合結果 通過擬合結果服從正態分布求得各可靠性指標95%置信區間及均值,見表4。 表4 接觸網系統三狀態天氣下可靠性指標計算結果 比較表4中三狀態天氣下接觸網系統平均故障時間間隔可知,不考慮天氣狀態時接觸網系統平均故障時間間隔為0.401 1 a,災難天氣時系統平均故障時間間隔均值為0.008 025 a,惡劣天氣時系統平均故障時間間隔值為0.088 25 a,正常天氣時系統平均故障時間間隔為0.722 0 a,顯然不考慮天氣時系統平均故障時間間隔與災難天氣時系統平均故障時間間隔相差較大,系統修復率與故障率以及可用率也存在類似規律,故在對接觸網系統進行可靠性評估時考慮天氣狀態十分必要。 本文以高速鐵路接觸網系統為研究對象,建立三態天氣下可靠性評估模型,并運用可信性理論求解不同天氣狀態下系統可靠性指標,以寶成鐵路長年統計數據進行算例分析,對該方法實用性進行驗證,得出如下結論: (1)不同天氣狀態下可靠性指標存在較大差異,在接觸網可靠性評估中,分別求取不同天氣狀態下可靠性指標十分必要。該方法只需統計周期內平均故障率與修復率以及不同天氣狀態持續時間占統計周期百分比即可求取不同天氣狀態下接觸網系統可靠性指標,能夠克服現場難以得到不同天氣狀態下元件故障率、修復率的問題,減少現場數據統計工作量。 (2)將不同天氣狀態下故障率與修復率看作一個隨機模糊變量能夠直觀地反映其模糊性與隨機性,不同模糊區間上下限對計算結果有一定影響,計算時可將統計周期內幾個日歷年中λavg、μavg的最大值作為模糊區間上限,最小值作為下限,均值作為可能性最大值,從而保證數據完整性,貼近現場實際情況,這對我國運行時間短,缺少實際統計數據的高速鐵路可靠性評估有一定實用價值。3 考慮天氣狀態接觸網可靠性評估
3.1 接觸網系統GO圖的建立
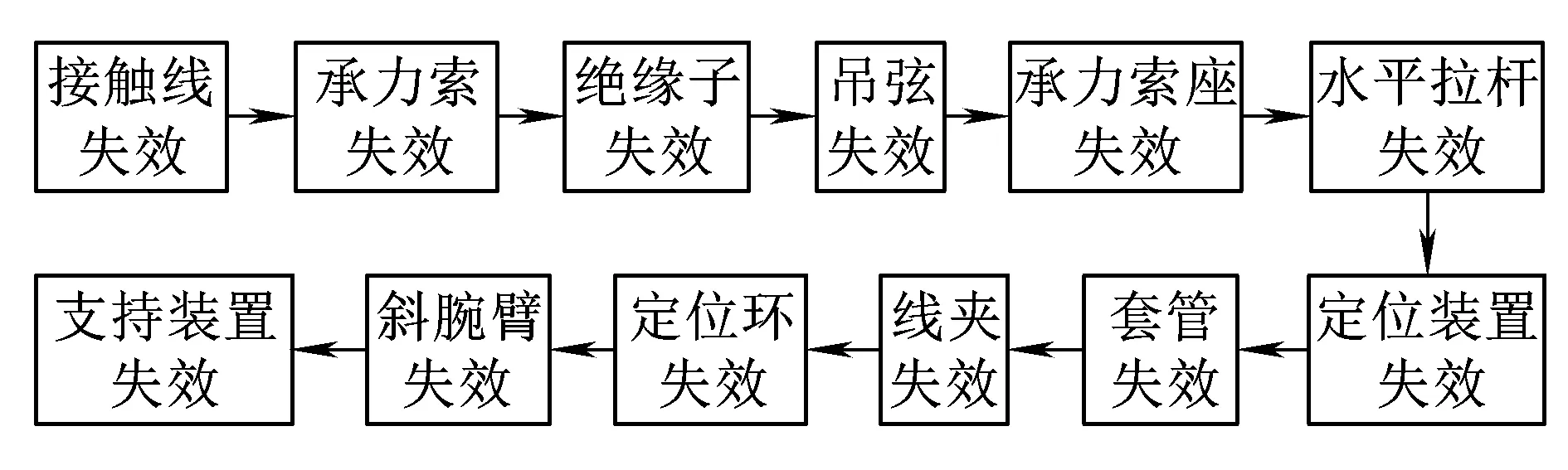
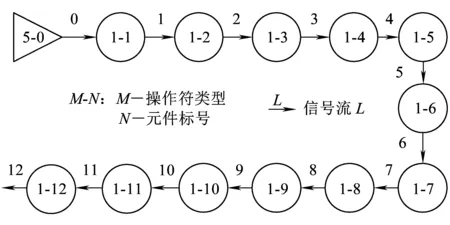
3.2 三態天氣下系統可靠性指標計算
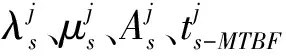
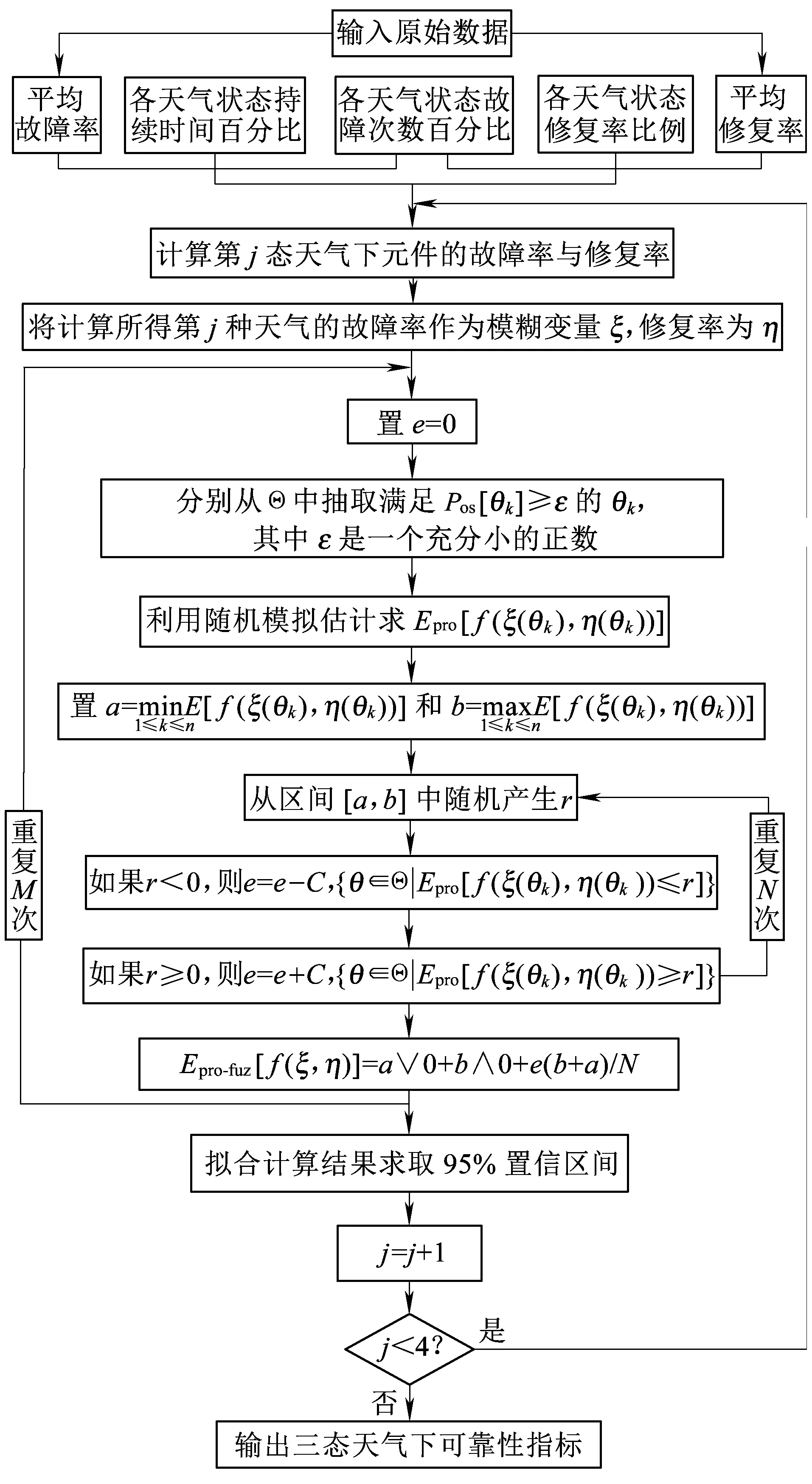
4 算例分析
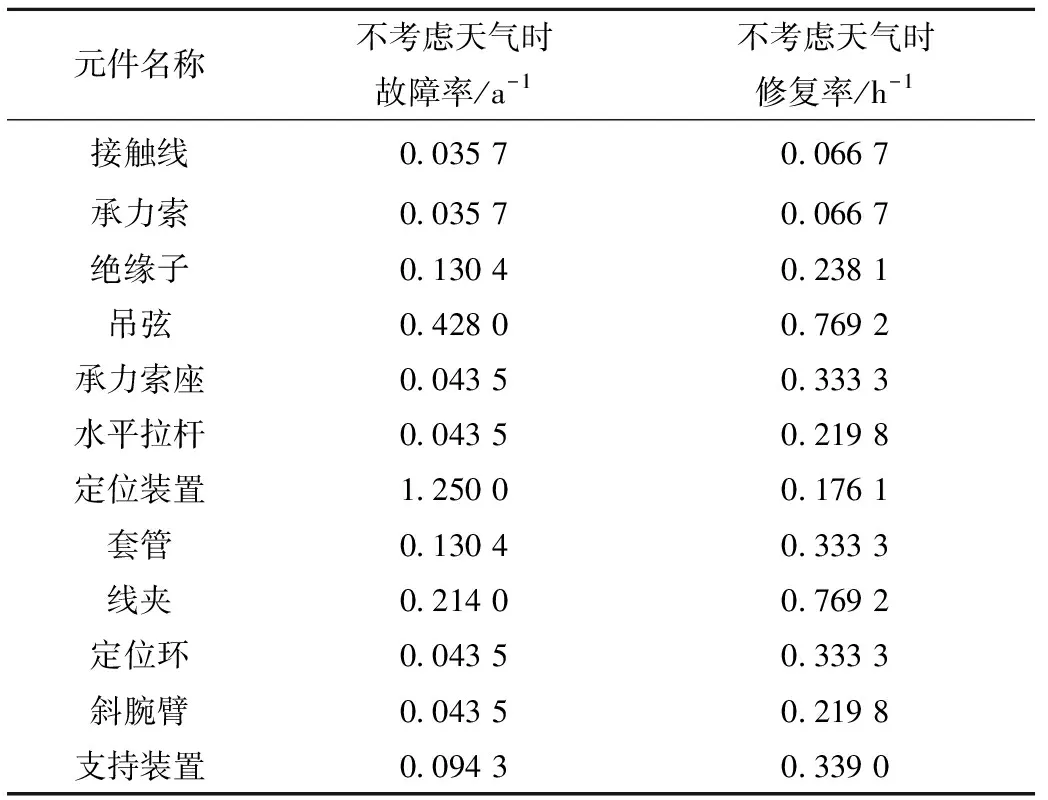
4.1 模糊變量表示形式對計算結果的影響

4.2 模糊區間范圍對計算結果的影響
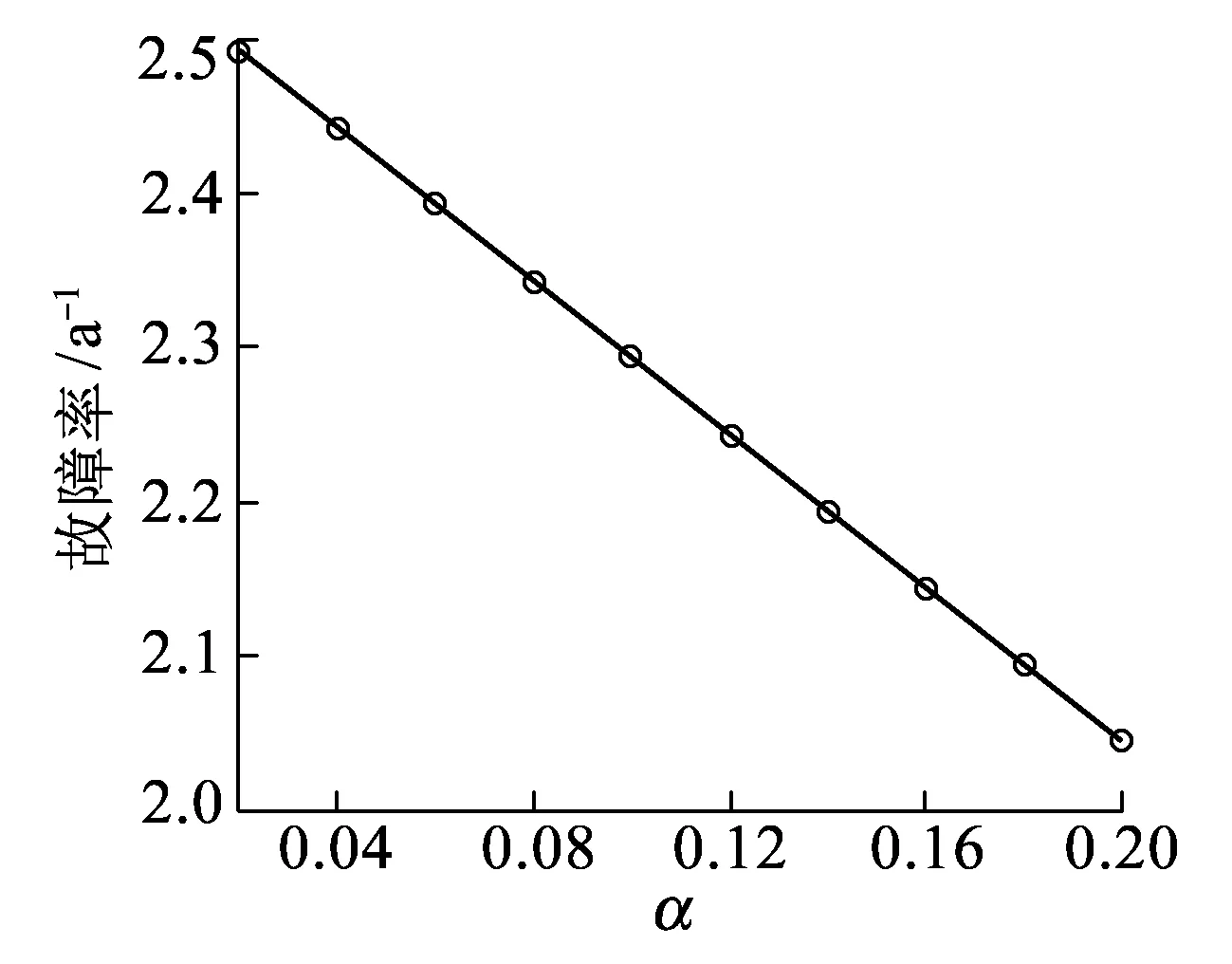
4.3 三態天氣下系統的可靠性指標計算
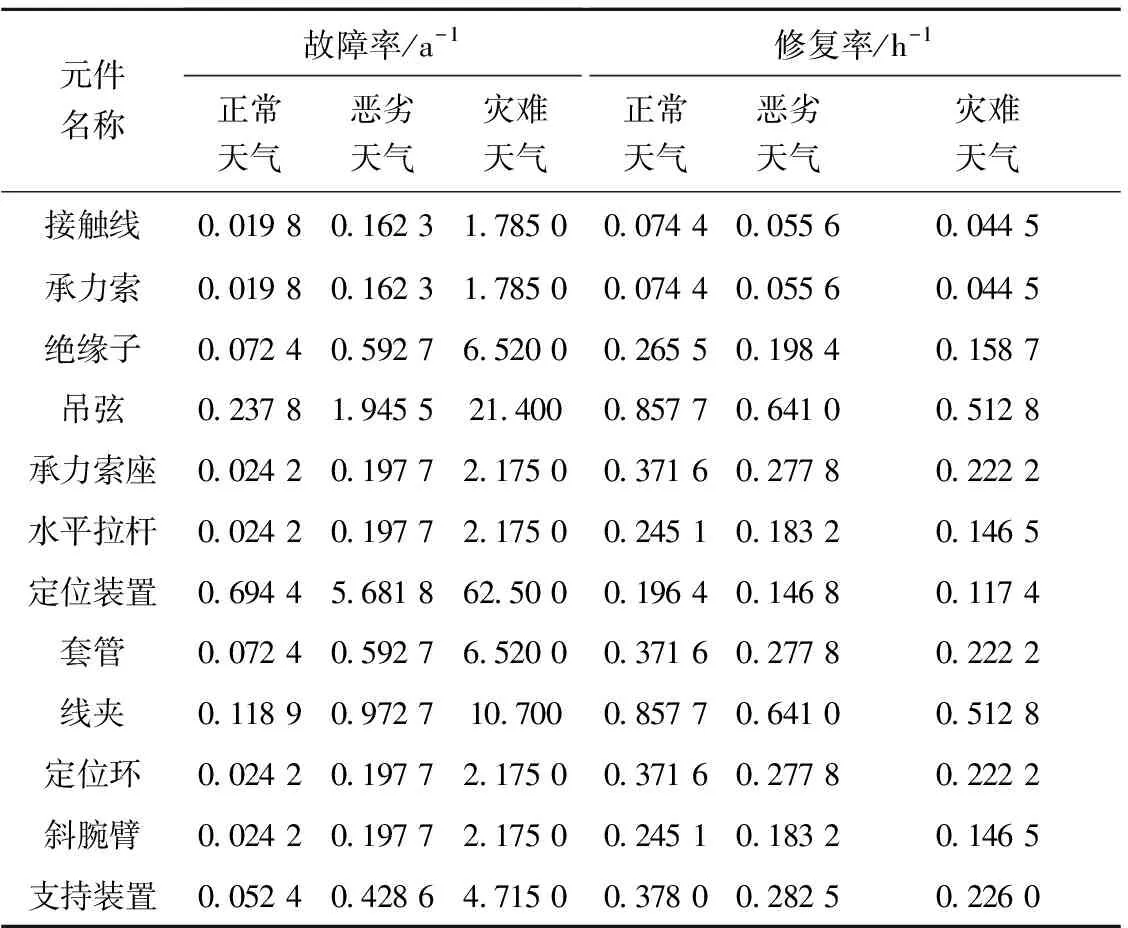
5 結論

