幾何模型構造法的解題策略探討

陳志惠

（漳浦達志中學，福建 漳州 363208）

一、初中生在幾何解題中存在的常見問題

學會正確的數學思考、數學構造、數學表達是學生數學素養的重要體現。而學生在解題中存在的問題核心也是這三點。

1.面對試題百思不得其解，是對幾何模型不熟悉的體現

幾何的基礎是基本的幾何圖形，而基本的幾何圖形可以構造出各種不同的模型，從而衍生出各式各樣的試題。我們在平時的教學過程中，或在輔導學生解題時，只是就題論題，一味解題，而沒有及時總結、歸類，提煉模型、方法、解題策略，最終可能并不會有太多收獲。特別是在遇到模型疊加及綜合時，能否可以準確判斷出相關模型及問題的切入點，決定了一道試題能否在規定時間內被攻破。只有掌握了各種幾何模型的通法解法，才能使我們快速地找到解題思路。

2.不會添加輔助線，往往是對重要關鍵詞不敏感

幾何壓軸題，往往注重多種幾何模型綜合、靈活運用。而幾何模型的綜合，有時并不會完整地展現幾何模型，題目中可能只會展現模型中最基礎的、關鍵的一部分圖形，因而，這就需要我們能捕捉到這些關鍵字眼或關鍵的圖形信息，找到顯性或隱性的已知條件，并能在大腦中反應出可能的基本幾何模型，通過添加輔助線構造出可能的基本幾何模型，通過在模型通法中，挑選出正確的做法。

3.解題過程漏洞百出，是因為推理邏輯不清，對模型通法不熟

解題過程容易出現邏輯錯誤，是因為我們的推理能力不足，邏輯思維混亂，對模型的條件、結論及推理過程不熟，也就是說對圖形的數學本質沒有深入的認識和理解。在解題教學中，應注重對試題的數學本質，圖形的數學本質進行鉆研和挖掘，讓學生清楚知識的來龍去脈，經歷知識的產生、推理、運用過程，注重步驟的規范書寫，注重綜合法、分析法的綜合運用，發展演繹推理能力和邏輯推理，滲透數形結合思想，發展幾何直觀，養成良好的數學學習習慣。

二、幾何模型構造法的解題策略探討

1.解題策略之“巧用圖形的對稱性構造對稱全等”

數學教材是一切數學教學活動的出發點，深入理解教材對我們的教學有重要的作用。我們在使用數學教材時，不難發現，教材對圖形性質的探索，無論是從點、線、面、體的探索，到線段、射線、直線、相交線、平行線的性質探索，或是線段的垂直平分線、角平分線、等腰三角形的性質探索，或是平行四邊形、菱形、矩形、正方形、圓的性質探索，無不是從圖形的對稱性入手的，通過折紙、畫圖活動，讓學生經歷觀察、猜想，測量、計算、推理、驗證等一系列探索過程，從而培養學生的幾何直觀能力，認識幾何模型，達到對圖形數學本質的認識，形成能力和思維。因此，對稱性是探索圖形性質的重要方法，也是解決圖形問題的重要思路。

（1）巧用圖形對稱性解題之“角平分線模型”

角平分線模型最主要的解題策略是構造對稱全等，利用圖形的對稱性、全等的性質進行問題的轉化、推理、計算，是初中數學非常重要的解題方法，而常見的對稱構造法有以下幾種情況：

例題1：已知：AD平分∠BAC，BD⊥AD. 求證：∠ABD= ∠DBC+∠C （如圖1）

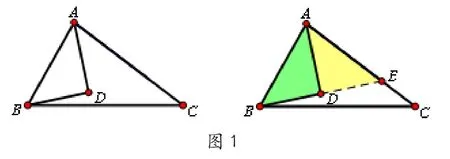
解題策略是利用角平分線的對稱性，當角平分線遇上垂直時，可以順延，得到等腰三角形。即構造對稱全等解決問題。

例題1變式1：已知：OP平分∠MON，PA=PB. 求證：∠OAP+∠OBP=180°（如圖2）

解題策略是利用角平分線的對稱性，角平分線上的點向角的兩邊作垂線，構造對稱全等解決問題。

例題1變式2：ΔABC中，AD平分∠BAC，∠C=2∠B. 求證：AB=AC+CD（如圖3）

解題策略是利用角平分線的對稱性，當證明線段的長度關系時，截長補短法是重要的解題思路，問題的本質也是構造對稱全等。

從上例可以看出，當題目中有直接給出或隱含的角平分線條件時，除了構成等角外，還應特別注意從角平分線兩個方面的功能來分析和認識圖形：① 以角平分線為軸，構成怎樣的對稱圖形？② 以角平分線和平行線結合，構成怎樣的等腰三角形？思考若以這樣的功能作指導，大都會找到恰當的解決方法。

（2）巧用圖形對稱性解題之“將軍飲馬模型”

最值問題、最佳方案是數學思考的一個重要方面，它為生活帶來便利，體現數學與生活的密切聯系。將軍飲馬模型是數學最值問題中的一個重要模型，它蘊含著幾何直觀、空間觀念的培養；轉化、化歸思想的滲透；對稱性解題策略的運用；幾何推理與計算在實際問題中的運用等，對稱構造是將軍飲馬模型的主要解題策略。

如圖，A、B是直線l外的兩個定點，在直線l上求作點P，使PA+PB路程最短。

例題2：如圖4，正方形ABCD的面積為12，△ABE是等邊三角形，點E在正方形ABCD內，在對角線AC上有一點P，使 PD＋PE 的和最小，求這個最小值。

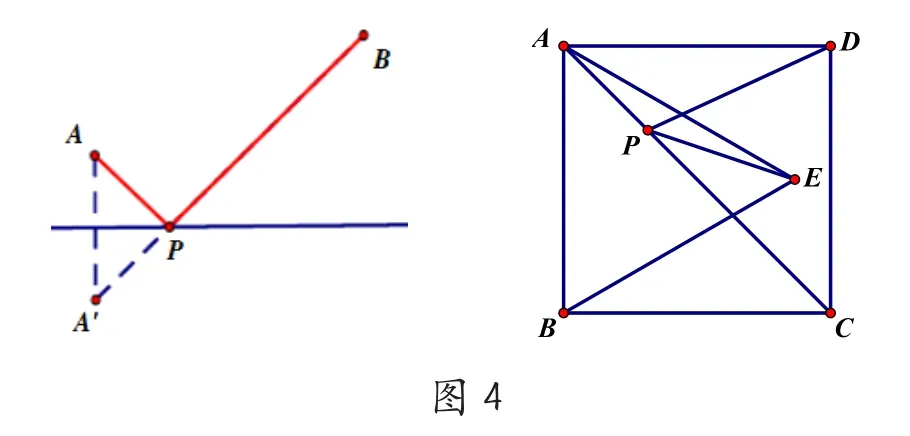
將軍飲馬題型的解題策略是利用軸對稱的性質作對稱點，原理是利用三角形的兩邊之和大于第三邊，解題技巧是化折為直，即口訣法：分清動定點，動點成直線，定點來照鏡，隔線把點連。

2.解題策略之“幾何模型構造法，運用模型通法解題”

“一題多解，解法優化；一題多變，變中求同；多題一法，同模通法”是數學解題與習題教學中重要的教學方法，也是學生學習的方法。對各個數學知識模塊，進行這三個維度的探究教學，有益于學生的數學思維能力的培養。

（1）巧用幾何模型一題多解，多解歸一

一題多解可以幫助學生開闊思路，把學過的知識和方法融會貫通，可大大提升分析問題和解決問題的能力；可以培養學生靈活、敏捷的思維能力，讓學生學會對問題進行多角度、多層次的分析，達到對問題的全面理解，進而迅速準確地解決問題；可以培養學生的發散性思維及聯想能力，學會用不同的知識解決同一個問題，達到對多種知識的融會貫通。

例題3：正方形ABCD中，CD=2，點P在以AC為直徑的半圓上，AP=1，∠DPC=45°，求點D到PC的距離。（如圖5）

解法1：利用幾何計算三大法寶之一“勾股定理”列方程求解。解題策略：遇垂線，求長度，勾股定理少不了！解法2：利用幾何計算三大法寶之二“相似列比例式”求解。解題策略：求長度，構相似，隱藏信息是關鍵！解法3：利用幾何計算三大法寶之三“銳角三角函數”求解。解題策略：求長度，找角度，三角函數來幫忙！解法4：手拉手，現全等。解題策略：撥開迷霧，圖形看本質，手拉手，現全等！解法5：對角互補，四點共圓或旋轉解題。解題策略：遇等邊，共頂點，全等旋轉是關鍵！解法6：相似變換，一轉成雙。解題策略：一對共頂點的相似三角形繞公共頂點旋轉可得另一對相似三角形，簡稱：“一轉成雙”，用旋轉變換構造相似形三角形，是把分散的邊角條件集中到特殊圖形中，以使其產生聯系。

例題4：正方形ABCD的邊長為4，P是AC上的一個動點（不與A、C重合），連接BP，將BP繞點B順時針旋轉90o到BM，連接MP，并延長交BC點E，交AD（或AD延長線）于點F.（如圖6）

（1）連接CM，證明：AP=CM；

（2）設AP=x，CE=y，試寫出y關于x的函數關系式；

（3）猜想PF與EM的數量關系，并證明你的結論．

撥開迷霧，圖形看本質。第（1）題是手拉手模型，手拉手，現全等。第（2）題是一線三等角模型，問題的本質是相似。第（3）題解法多樣化，可以利用不同的幾何模型通法，從而達到一題多解。解法1：截長法構造全等。解法2：補短法構造全等。解法3：角平分線構造對稱全等。解法4：手拉手和角平分線結合構造全等。解法5：利用手拉手和對角互補模型。解法6：利用三垂直模型全等。解法7：三垂直模型和平行線分線段成比例相結合。解法8：手拉手和角平分線構造對稱全等。通過一題多解，把學過的知識和方法融會貫通，從而提升對試題本質的認識，提高解題能力。

（2）一題多變，變中求同；多題一法，同模通法

課本例題、習題為學生開拓思維提供了豐富的資料，是教師開展變式教學的重要資源，其思維方式的典型性、解題過程中的示范性是課外習題不能比擬的。課本例題、習題是許多中考題的原始來源，例題、習題的拓展常常成為中考的考點。我們可以通過很多途徑對課本的例題、習題進行變式。如：改變條件、改變結論、改變數據、改變圖形；條件引申、結論拓展；條件開放或結論開放，或條件、結論同時開放等。

例題5：如圖，四邊形ABCD中，∠ABC=∠A DC=90o，BD平分∠ABC，∠DCB=60o，AB+BC=8，求AC的長。（如圖7）

變式一：改變圖形背景。如圖，⊙O的直徑AB為10cm,弦AC為6cm，∠ACB的平分線交⊙O于D。（1）求BC的長；（2）求AD,BD的長。

變式二：保留結論，更換條件。如圖，⊙O的 弦AB長10cm,∠ADB=90°， 弦AC長6cm，AD=BD（1）求BC的長；（2）求AD,BD的長。

變式三：保留條件，結論拓展。如圖，⊙O的直徑AB為10cm,弦AC為6cm，∠ACB的平分線交⊙O于D。求CD的長。

變式四：把等腰直角三角形換成等邊三角形。

變式五：把等邊三角形換成正方形。

變式六：把正方形換成正多邊形。

認識和體會數學是一個整體，變式例題（習題）教學應該突出變式中的共性，切忌就題論題，應引導歸納總結，通過特殊去發現一般規律，能“解一題，懂一法，會一類，通一片”。

3.解題策略之“聯想構造法：運用中點模型解題”

中點是幾何解題中常常遇到的，特別是三角形的中點、中線、中位線及直角三角形斜邊上的中線等是高頻考點，是中考的必考內容。遇到中點，我們應從哪些方面進行思考呢？

以直角三角形斜邊上的中點為例，請看例6、例7，尋求中點模型的構造法。

例題6：□ABCD中，AB=3，BC=4，E為□AB CD外一點，∠AEC=∠BED=90o。（如圖8）

（1）求□ABCD的面積。

（2）求四邊形ABCE的面積的最大值。

例題6變式：在Rt△ABC和Rt△ADC中，∠ABC=∠ADC=90o，E、F分別為AC和BD的中點。（如圖9）

（1）求證：EF⊥BD。

（2）若∠BAD=45o，求AC：EF的值。

例題7：已知：AD、AE分別是△ABC的高和中線． （如圖10）

（1）若AC=2DE，求證： ∠C=2∠B。

（2）若∠C=2∠B ，求證：AC=2DE。

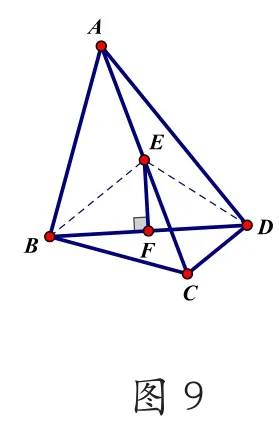
例題6由兩個直角聯想到直角三角形，想到連接對角線，而矩形使得兩條斜邊有了聯系，因此，共中線等斜邊是本題最大的特點，也是需要學生發現的地方；例6變式和例6區別在于共斜邊而得到等中線，和例6是條件結論互換，解題策略為：（1）共中線、則等斜邊；（2）共斜邊，則等中線。例7由已知中點，需要聯想構造，使高和中線產生聯系，從而使問題得到解決；（3）知中點，作中點，中線和中位線完美結合。一個中點不夠，再構造一個中點，使分散的已知條件集中。