高中數學空間想象誤區案例分析及應對

林玉輝

（詔安第一中學，福建 漳州 363500）

高中是走進大學或是社會的一道門檻，高中時期的學習對學生們由初中到大學或是社會有著過渡的重要作用。［1］新的高中數學課程標準提出六個核心素養，其中直觀想象是指借助空間想象感知事物的形態與變化，利用幾何圖形理解和解決數學問題。主要包括：利用圖形描述數學問題，建立形與數的聯系，構建數學問題的直觀模型，探索解決問題的思路。［2］

可是，有的學生由于很少關注周圍的空間環境，缺乏觀察分析能力，空間想象能力、動手操作的能力較弱，空間概念模糊，對空間想象產生誤區，無法解決空間立體幾何問題。這里，筆者就學生常見的空間想象誤區加以分析，以便教師在教學中有所啟示。

一、學生空間想象誤區的背景

普遍高中學生怕立體幾何，表現在怕畫圖、怕想象、怕計算（特別是二面角的問題）。其中空間想象是核心問題，不少學生經常出現空間想象誤區，導致思維障礙，解題困惑。

立體幾何要求學生能夠判斷空間點、線、面之間的位置關系，特別是線與線，線與面，面與面的平行與垂直的位置關系以及它們之間的相互轉化，能夠借助簡單幾何體（如空間四邊形、平行六面體、正方體、長方體、棱柱、棱錐等）作為載體，把空間的點、線、面等基本元素有機地結合起來，解決空間的角、距離、面積、體積等問題，形成一個比較完整的立體幾何的知識體系，提高學生的空間想象能力。可是，由于學生接觸立體幾何的時間較短，而三維的空間圖形無法在平面內直觀地表現出來，很多學生對于空間幾何圖形往往無法想象，知識積淀較少，動手實踐經驗不足。因此，重視學生空間想象誤區的分析，引導學生科學合理地判斷空間點、線、面之間的位置關系，提高學生空間想象能力是高中數學教師教學的重難點。

二、常見學生空間想象誤區案例分析

（一）借助二維的平面圖形，對線與線、線與面位置判斷的失誤

由于我們借助于平面的圖形表示三維的空間，導致學生對異面直線錯誤的判∪斷。如圖1，平∪面 a∩平面=直線AC，直線ABa，直線CD，那么直線AB與CD是異面直線，但由于畫在二維的平面圖上兩條直線確實是“平行”的，無法體現兩條直線的真實位置關系，導致想象誤區——錯誤的判斷AB∥CD.

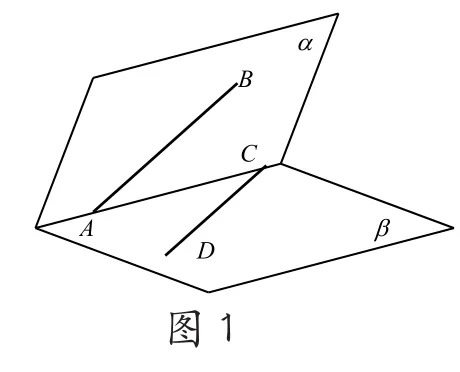
（二）把非直角誤認為直角，而把直角視為非直角

應用斜二測畫圖把空間圖形轉化為二維圖形，由此導致角度的變化，學生判斷失誤。如圖2，在三棱錐P-ABC中，PA⊥平面ABC，且PA=1，AB=5，AC=3，BC=4，求點A到平面PBC的距離。很多學生找不到距離，采用建立空間直角坐標系，把∠BAC誤認為是直角。

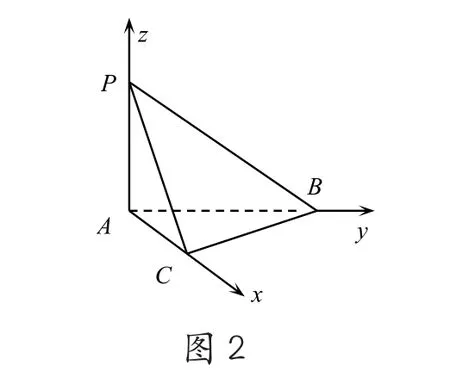
（三）平面幾何結論隨意應用到立體幾何里

在初學立體幾何時，很多學生受到平面幾何的影響，想當然地把平面幾何的結論隨意套用到立體幾何里，缺乏對空間圖象的分析。例如：

1.在平面幾何里，四條邊相等的四邊形是菱形，可是在空間里可能是空間四邊形。

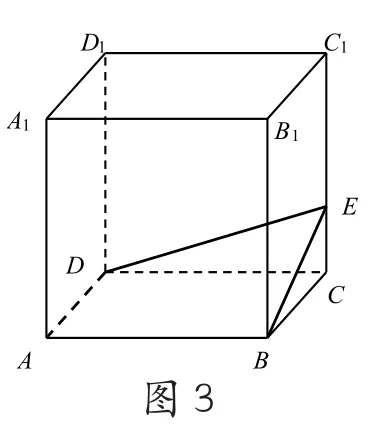
2.有三個角是直角的四邊形是矩形，但在空間里不一定就是矩形了，如圖3，在長方體ABCD-A1B1C1D1中，點E在棱CC1上，顯然∠BAD=∠ABE=∠ADE=90，而四邊形ABED是空間四邊形，不是矩形。

3.在平面幾何中，和線段兩個端點的距離相對的點集合是該線段的垂直平分線，而在空間里卻是垂直平分面。

4.在平面幾何中，過一點與已知直線垂直的直線有且只有一條，但在空間就存在無數條了，等等。

（四）畫圖的不合理，導致空間想象的錯誤

有的學生畫立體幾何圖形往往忽視了畫圖的基本要求，如水平放置的橫坐標長度不變，縱坐標變為原來的一半，被擋住的部分需要畫成虛線，輔助線的畫法與初中不同（初中平面幾何的輔助線一律畫成虛線，立體幾何是看不到的線畫成虛線），所以往往導致計算或推理失誤，造成解題困難。

（五）概念理解不透徹，出現空間想象誤區

例如：1.各個面都是正三角形的多面體誤斷為正多面體。

2.如圖4，在直三棱柱ABC-A1B1C1中，E是AC的中點，AB1⊥BC1，求二面角E-BC1-C的大小，該題是1994年全國高考第理科第23題，很多考生就把∠EOC誤認為二面角E-BC1-C的平面角。

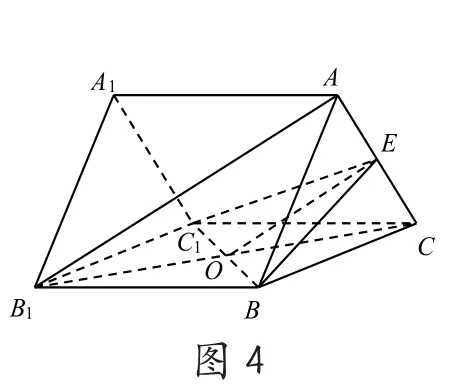
（六）定理誤用，出現計算錯誤

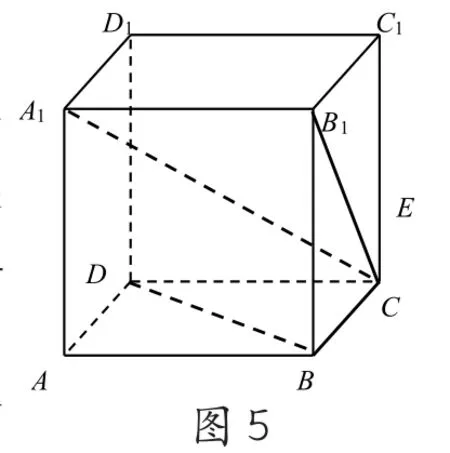
對于異面直線所成的角與三垂線定理混淆，誤認為是異面直線在同一平面內射影的夾角，如圖5，在正方體ABCDA1B1C1D1中，異面直線A1C與BD的夾角誤斷為它們在平面

BCC1B1內的射影B1C與BC的夾角45（正確答案應為90）。

（七）空間想象欠全面、不仔細，導致判斷失誤

例如：1.棱長都相等的四棱錐的底面誤斷為菱形，孰不知由于側棱也相等，那么頂點在底面內的射影恰好是它的外接圓圓心，由此判定它的底面是一個正方形，故這樣的四棱錐是一個正四棱錐。

2.底面是正三角形，側面是等腰三角形的三棱錐誤斷為正三棱錐（欠全等的條件）；底面是正方形，側面是全等三角形的四棱錐誤斷為正四棱錐（欠共同的頂點）；底面是正三角形，側面面積都相等的三棱錐誤斷為正三棱錐（欠頂點在底面的射影在底面三角形內）。

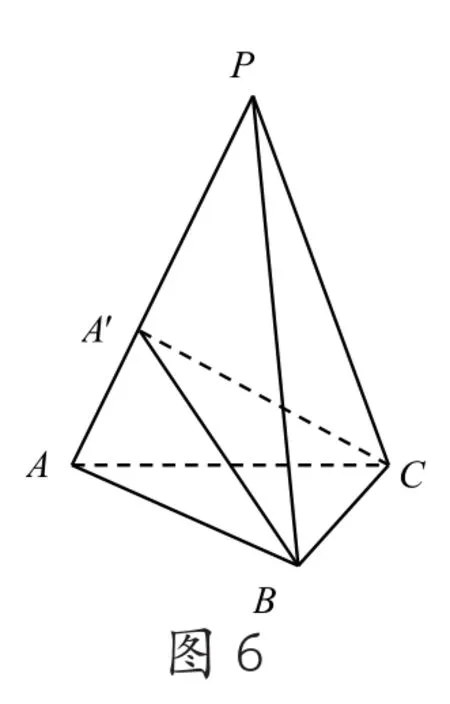
3.底面是正三角形，側棱兩兩的夾角相等的三棱錐誤斷為正三棱錐。其實，如圖6，在正三棱錐P-ABC中，只要在側棱PA上取一點A'，使BA=BA'，那么，三棱錐P-A'BC就滿足題設要求，但顯然它不是正三棱錐。

（八）線面垂直、面面垂直判定條件不充分

很多學生在判斷線面垂直時經常和判斷線面平行的方法混淆，只找到直線與平面內的一條直線垂直就推出線與面垂直，條件不充分；判斷面面垂直時，只在兩個平面各找出一條直線互相垂直就草率地判斷面面垂直。

（九）面對幾何體的展開圖無法還原

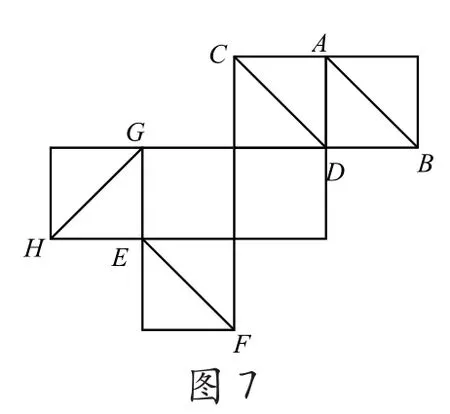
如圖7，是一個正方體表面的一種展開圖，圖中的四條線段AB、CD、EF和GH在原正方體中相互異面的有多少對？（2002上海春季高考）， 很多學生無法還原成原來的正方體，無法判斷AB、CD、EF和GH在原來的位置關系，特別是AB與CD，誤斷為平行共面。

三、引導學生走出“誤區”, 提高學生的空間想象能力

以上是學生經常出現的空間想象誤區案例，由此要求教師在教學中，應該及時發現學生作業和測試中出現的問題，尋找誤區的緣由，對癥下藥，引導學生走出“誤區”，逐步提高學生的空間想象能力。這里提幾點建議供參考：

解決策略一，針對上面的誤區（一）（二）（四）（九），教學板書時注意畫空間圖形的合理化、科學化，盡量使平面的圖形立體化，把立體幾何問題平面化，歸結為平幾問題解決；

解決策略二，針對上面的誤區（一）（二）（四）（七）（九），課堂教學時盡量借助實物或教具模型教學，或使用多媒體教學的手段，例如經常舉例日常生活中的幾何體，可以增強學生的空間想象能力，對空間幾何體的想象更直觀；

解決策略三，針對于誤區（三）（八），課堂教學時注重知識的聯系，經常設置一些容易誤解的題目；例如，判斷下列各題的正確性

（1）經過直線外一點，與該直線平行的直線有且只有一條…………………………………………（√）

（2）經過一點，與已知直線垂直的直線有且只有一條………………………………………………（×）

（3）經過平面外一點，與該平面平行的直線有且只有一條…………………………………………（ ×）

（4）經過平面外一點，與該平面平行的平面有且只有一個…………………………………………（√）

（5）直線與某個平面內的無數條直線垂直，則這條直線與該平面垂直……………………………（×）

解決策略四，針對于誤區（六），空間的角（特別是二面角）和距離的計算，引導學生建立適當的空間直角坐標系，把難以想象的空間問題轉化為代數問題來解決。

解決策略五，引導學生多采用類比，聯想轉化，把知識有機結合起來，指導學生會創新地學，從而更系統地掌握所學知識，建立完善的認知結構；要求學生善于分析和轉化，把空間的問題轉化為平面的問題來解決。

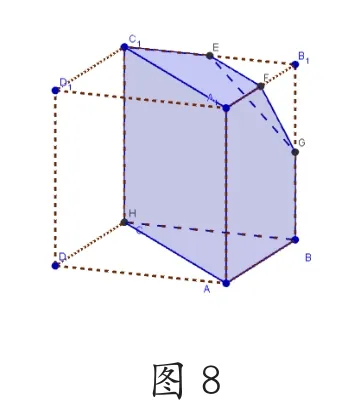
解決策略六，在引導學生走出各種誤區的最有效辦法就是信息技術與教學有機結合，建議教師利用GeoGebra軟件（簡稱GGB軟件）中的3D功能，從不同角度感受幾何體的情景，因為在立體幾何與圓錐曲線演示的操作中更加簡便，［3］下面是筆者根據某地的一道三視圖利用GGB制作的直觀圖，從不同角度觀看的截圖。（圖8、圖9、圖10）

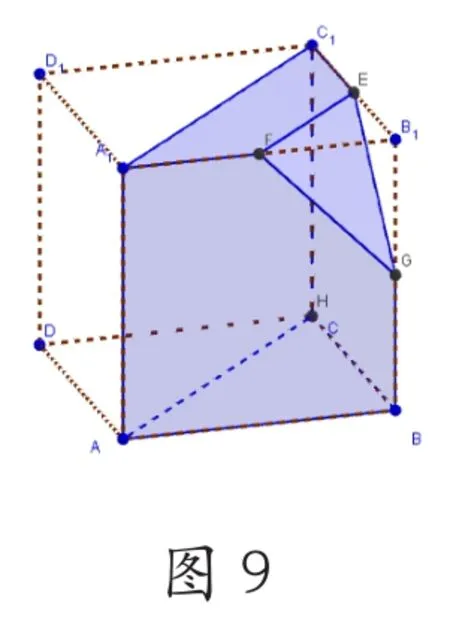
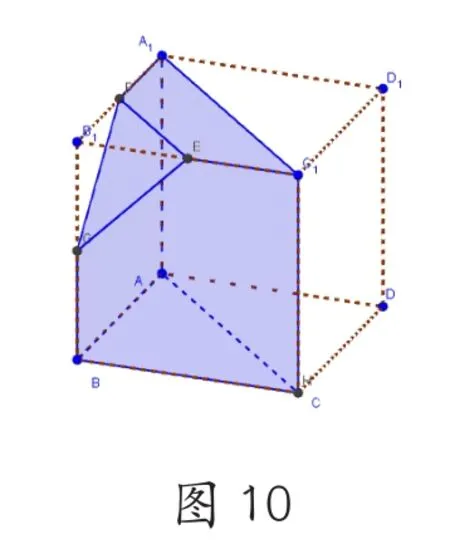
總之，在高中立體幾何教學過程中，教師應該了解掌握學生的空間想象誤區，引導學生動腦，動手，動筆，課堂上多方位指導學生認識幾何體，課外強調學生從實際出發，認真實踐總結，不斷加深對幾何體的認識，走出誤區，提升學生的直觀想象素養。