一種基于軟件觀測器的低速直驅伺服系統控制策略

顧佳輝，周 杰，顧加鵬，李 寧

（南京工程學院，江蘇 南京 210013）

0 引言

交流伺服系統多以稀土永磁同步電機（PMSM）為驅動對象[1]，是當今社會的生產制造業走向自動化和智能化的基本構成元素，多用于軌跡跟蹤控制技術，因為低速狀態下，交流伺服系統的工作特性顯得尤為重要。所謂低速直驅[2]，指的是在低速狀態下的交流伺服系統，不使用減速機構，與機械負載直接耦合驅動，可以省去中間環節，增加控制精度，有著更快的響應速度。

應用環境對于低速直驅伺服系統的性能有著很高的要求，主要是對速度平穩和轉矩性能方面要求速度平穩和輸出轉矩接近額定值。在現代伺服系統控制過程中，一般的位置檢測采用的光電編碼器[3]，光電編碼器有著體積小，精密和分辨率高等優點，可以精確的檢測常規伺服系統的角度位置，但在惡劣的條件下需要相當完善的保護措施，而在低速環境下對位置檢測的要求非常高，光電編碼器會因為機械間隙的問題在低速狀態下出現角度檢測較大誤差的現象，其精度變低，控制效果變差[4]。

本文就低速直驅控制系統進行研究，從加強角度檢測的方面來增強對低速直驅伺服系統的控制效果。在硬件光電編碼器控制優點的基礎上，提出了軟件觀測器進行輔助測量角度，通過控制算法來實現對反饋角度的精確測量。

1 軟件檢測器的實現原理

1.1 光電編碼器位置測量值

（1）測速原理：光電編碼器是一種通過光電轉換將輸出軸上的幾何位移量轉換成脈沖或者數字量的傳感器，本文編碼器用于讀取伺服電機的轉角值，一旦電機開始運動，電機主軸開始旋轉，編碼器內部會不停的產生告訴脈沖，此脈沖為計數作用，隨著電機主軸的速度變化，讀取的脈沖數也響應的不同，所以光電編碼器通過單位時間內的脈沖響應數量經過一定的計算可以得到轉速n。

（2）測量方法：光電編碼器是通過讀取脈沖數來進行測量。傳統的測量方法有三種，分別是M法，T法和M/T法，三種方法各有優勢，為了應對文本的低速條件，本文采取T法進行相應測量轉角。T法是通過測量光電編碼器輸出信號的周期Tf來推算電動機的轉速，只要汲取在一個光電脈沖周期Tf內的高頻脈沖個數m2，就可以測出光電脈沖周期Tf的長度，從而得到電動機的轉速。具體公式如下：

式中：f—高頻脈沖頻率；pf—光電編碼器分辨率，這里面的4為本文采用四倍頻信號處理；kω—速度反饋系數；m—脈沖個數（此值為光電編碼器測量值）。

由于電動機的轉速與測量值m成反比，電動機轉速越高，m就會越小，故T法的選擇最適合本文的應用環境。

1.2 電機轉角計算值

在交流伺服電機軸上安裝光電編碼器用上述方法得到電機轉速，通過內部轉換，得到輸出的第k個周期的實測角度信號 θ（k），k=1，2，3…，以此測出來的實測角度信號θ（k）作為間接觀測值的參考信號，計算第k個控制周期的間接觀測偏差△（k）=θ（k）-θ（k），其中（k）表示第個周期的轉角觀測值；將交流伺服電機動力學離散化，就可以得到交流伺服電機的速度觀測值（k+1）和轉角觀測值（k+1）的遞推公式：

其中，s—拉氏算子；J—轉動慣量；B—粘性摩擦系數，△是采樣周期，λ=△/J；

2 軟件檢測器的實際運用

本文提供了一直低速直驅下的軟件計算方案，控制原理如圖1所示。包括了位置閉環、速度閉環、q軸電流閉環和d軸電流閉環。對低速直驅式交流伺服系統的輸出電流ia、ib進行檢測，并通過旋轉變換得到交軸電流iq和直軸電流id，分別用于q軸電流閉環反饋和d軸電流閉環反饋。

這里面旋轉變換的角度視為交流伺服電機轉子的轉角，在本文中該轉角通過間接觀測得到。當采用直軸電流id=0的控制策略時，交軸電流iq與低速直驅式交流伺服系統的電磁轉矩成正比，而低速直驅式交流伺服系統中的交軸電流給定信號iq*是可以實時的獲得的，在這種基本條件下，解決角度準確度的問題，方法就在于實現對交流伺服電機的動力學模型和交軸電流控制模型的數學重構就可以間接觀測交流伺服電機的速度和轉角位置等，此設計理念則為軟件觀測器的實現。具體設計框圖如圖2所示。

一般情況下，交流伺服系統的電流環具有足夠的帶寬，因此只有轉動慣量J和粘性摩擦系數B是影響轉角、轉速間接測量環節的系統參數，在轉角、轉速間接測量環節中使用的參數值和實際參數之間會存在一定的誤差，可能導致測量值與實際值參數之間的偏移，通過轉矩補償信號來補償。通過光電編碼器輸出的脈沖計數，可以得到交流伺服電機轉角的參考信號θ（k），將轉角的參考信號 θ（k）與轉角計算值（k）相比較，可以得到轉角觀測偏差△θ（k）=（k）-θ（k），觀測偏差△θ（k）經過轉矩補償控制器的計算，可以得到轉矩補償信號△M，轉矩補償控制器采用比例積分算法，補償控制參數包括比例系數和積分系數。計算交流伺服電機在第k個控制周期輸出轉矩的估計值 M（k）=iq*（k）·KT-△M（k），其中，iq*（k）為第 k 控制周期的交軸電流給定信號，KT為交流伺服電機的轉矩系數。在反饋環節我們采用PI調節器來進行補償角度誤差信號，該PI調節器即為負載轉矩補償器，該軟件觀測器主要是將轉角計算值進行同步輸出，轉角觀測值用于計算誤差偏移補償值，在該閉環中使用PI調節器可以更直接有效的消除偏差，實現準確的轉矩補償，該環節需要調節的是實際角度計算信號與實際檢測信號產生的偏差。該軟件觀測器具體實現如圖3所示。

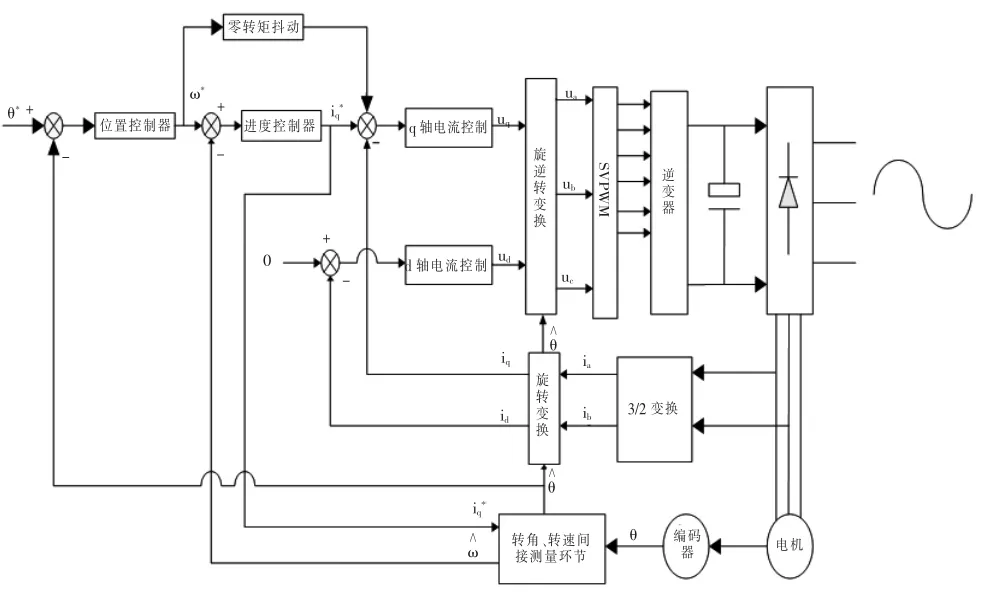
圖1 軟件觀測器的系統總框圖

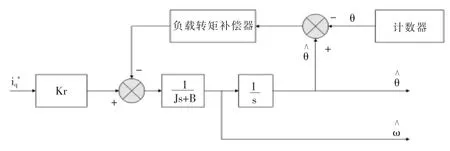
圖2 軟件觀測器流程框圖

圖3 軟件觀測器實現模型

3 仿真實驗研究

本文使用Matlab2014b對所設計系統進行仿真研究。所給定電機參數為：額定扭矩：0.32N·m，額定轉速：3000r/min，轉子慣量：0.037×10-4kg·m2，機械常數：0.75ms，扭矩常數：0.36N·m/A，電機阻抗：9.3Ohm，電機感抗：24mH。 設定仿真時間為16s。具體的設計總圖如圖4所示，該總體設計包括了初始信號發生模塊，軟件觀測器反饋模塊，電機動力學模型模塊三部分組成。運用實際的電機參數對測試波形進行仿真。

圖4 Simulink仿真總框圖

3.1 編碼器精度對系統誤差分析

實驗設定了反饋環節中的PI參數kp=20，ki=1.3，測試編碼器為1600p/rev，仿真時間16s，程序啟動后，可以看到得到位置信號和反饋的位置信號如圖5、6所示。編碼器分辨率160p/rev，其他不變時，結果如圖7、8所示。

由上圖對比可以看出，整體軟件觀測反饋的位置信號與實際信號的誤差范圍相當小，具有良好的穩定性，在編碼器精度相差很大的情況下，反饋信號沒有較大偏差，高方法對于解決編碼器精度的限制問題有著較好的控制效果。

圖5 編碼器分辨率1600p/rev位置結果

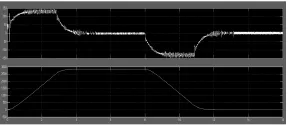
圖6 編碼器分辨率1600p/rev的速度和位置

圖7 編碼器分辨率160p/rev的位置

圖8 編碼器分辨率160p/rev的速度和位置

3.2 電機的轉子慣量對系統誤差分析

實驗設定了電機的轉子慣量先按照電機參數，即J=0.037×10-4kg·m2，編碼器統一設定為 1600p/rev，設定轉子慣量為 0.087×10-4kg·m2，實驗結果如圖 9、10 所示。

由上圖可以分析，在轉子慣量變換過大的情況下，位置信號，即間接反饋的轉子信號基本沒有變化，說明該反饋環節中轉子慣量的變化對整體系統的影響有一定的消除作用。該系統具有較好的魯棒性，完全驗證了本文閉環算法的實現可能性。

圖9 轉子慣量為0.087×10-4kg·m2時的位置結果

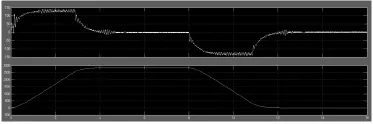
圖10 轉子慣量為0.087×10-4kg·m2時的速度和位置

4 總結

本文在傳統光電編碼器使用的基礎上，運用了軟件觀測器與之結合，通過差值計算的方法，得出更為精確的反饋角度，從而獲得較為連續的速度信號，在低速直驅伺服系統中得到了有效的使用。加大了系統測量反饋的精度，同時也更有效的緩解了低速狀態下反饋不準確導致的速度死區的問題，既簡單方便，又準確的實現了所需要的控制效果，提高了控制精度和電機運行的動態性能。