基于粒子群算法的石英撓性加速度計溫度補償方法研究

于東康，楊功流，吳宜榮，謝祖輝，涂勇強

(1.北京航空航天大學 儀器科學與光電工程學院，北京 100191；2.福建星海通信科技有限公司，福州 350015)

0 引言

光纖陀螺具備體積小、質量小、可靠性高、動態范圍大、線性度好、頻帶范圍寬以及啟動時間短等優點，以光纖陀螺和石英撓性加速度計為核心部件的光纖慣組，憑借其優越的性能廣泛應用于航天、航空、航海、兵器及多種軍民用領域[1]。

目前國內普遍使用的光纖陀螺、石英撓性加速度計其零位和刻度因子受溫度變化影響明顯，要使光纖慣組在全溫范圍內(一般為-40℃～60℃)的輸出滿足精度要求，必須盡可能地消除溫度變化對器件性能的制約[2]。目前常用的方法有兩種：1)采用溫控的方法為慣性器件加溫以提供良好的環境溫度條件；2)采用實時溫度誤差補償技術，對慣性器件進行實時補償以滿足其全溫范圍內的精度[3]。其中溫度誤差補償作為一種純數學的方法，相較于溫控法能夠避免結構的冗余，同時也能得到較高的補償精度，是目前采用較多的一種方法[4-7]。在對溫度誤差補償方法的研究工作中，文獻[4]利用數據擬合的方法建立了加速度計溫度模型，并應用該模型提出了相應的補償算法；文獻[5]提出了基于小波最小二乘支持向量機的石英撓性加速度計溫度補償方法；文獻[6]則建立了基于溫度和溫度梯度的聯合多項式補償模型，設計了基于傳統最小二乘擬合的補償方法。

在本文針對的工程實例中，慣組的石英加速度計精度較低(對應精度在1mg左右，屬低精度加速度計)，啟動后輸出穩定性受溫度變化影響較大，通過傳統的最小二乘補償方法無法得到滿足要求的補償精度，因而成為制約慣組精度的主要因素。

在經充分驗證此類低精度石英撓性加速度計靜態溫漂特性之后，本文提出了一種引入溫度、溫度高次項及溫度變化率作為變化量的溫度誤差模型，并設計了基于粒子群算法的溫度補償方法。通過搭建測試平臺驗證補償效果，試驗結果表明：該方法能夠有效補償石英加速度計的溫度漂移，使加速度計輸出的零偏穩定性提升1個數量級，具有良好的工程應用價值。

1 石英撓性加速度計溫度特性分析

1.1 石英撓性加速度計溫度特性

石英撓性加速度計表頭的結構如圖1所示，主要包括檢測質量組件、上力矩器組件和下力矩器組件三部分。在使用過程中，加速度計溫度漂移主要由表頭結構參數變化、封裝熱應力和檢測電路溫度漂移造成[8]。對于石英撓性加速度計來說，表頭部分是產生溫度誤差的主要原因，表頭溫度的變化和表頭力矩器標度因數的溫度系數決定著加速度計溫度誤差的大小。

在加速度計工作過程中，2個因素會直接導致其表頭溫度的變化：1)工作環境溫度的變化；2)由于力矩器線圈在通過反饋電流時自身發熱造成的表頭溫度變化。由自發熱導致的線圈尺寸和磁場強度變化由式(1)表示：

l=l0(1+β1ΔT)

B=B0(1+β2ΔT)

(1)

其中，l0和B0分別為常溫下(T=20℃)力矩器線圈的尺寸和磁場強度，l和B分別為溫度變化ΔT后力矩器線圈的尺寸和磁場強度，β1和β2表示線圈和磁鋼的溫度系數。

力矩器線圈自發熱引起的輸出誤差可表示為

δ=(1+β1ΔT1)(1+β2ΔT2)-1

(2)

基于上述分析，如果考慮加速度計零偏溫度特性模型是實時溫度T與百秒溫度變化ΔT的函數，即可表示為

K0=φ(T,ΔT)

(3)

式中，K0為加速度計的零偏。

1.2 石英撓性加速度計溫度補償模型

工程上使用的加速度計誤差模型為

N=K(K0+a+εa′)

(4)

式中，K為標度因數，a為對應軸向的輸入加速度，ε為安裝誤差項，而a′為輸入軸垂直方向上的加速度。

溫度變化帶來的影響主要為標度和零偏的變化，反映在公式上，則可將式(4)表示為

N(T)=K(T)(K0(T)+a+εa′)

(5)

如重點考慮對零偏的補償，即忽略溫度對標度因數的影響，采用先溫補再標定的工程方案。針對石英撓性加速度計溫漂特性，提出與溫度和溫度變化率有關的溫補模型

ΔN=aT+bT2+cT3+dΔT+eΔT2

(6)

式中，ΔN為補償量，亦即加速度計的零位漂移量，a、b、c、d、e為溫補參數。式(6)給出的模型結合了溫度場的變化速率以及不同溫度條件下的數據，能夠很好地反映速度計的溫度漂移情況[9]。

1.3 傳統最小二乘法擬合溫補系數

借助式(6)建立的溫度漂移模型，通過一定方法求取相關系數并加以補償，可以達到溫補目的。最小二乘法就是其中一種行之有效的擬合溫補參數的方法，也是工程上使用較多的傳統方法。

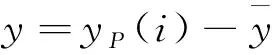
y=ΔN(T,ΔT)=aT+bT2+cT3+dΔT+eΔT2

(7)

式(7)為關于T和ΔT的二元三次多項式。根據最小二乘法的定義，就是要通過給定的數據(Ti,ΔTi,yi)確定其中幾個系數，使得在各個點上的偏差δ平方和∑δ=∑[∑ΔN(Ti,ΔTi)-yi]2達到最小。

利用Matlab提供的regress函數，可以實現最小二乘擬合求參，該方法特點為使用便捷，無需復雜的調參步驟，但同時得到的補償精度有限，在某些工程環境下難以滿足需要。

2 粒子群算法用于溫漂補償

2.1 粒子群算法基本原理

粒子群算法(Particle Swarm Optimization，PSO)是模擬鳥群捕食行為的一種算法。該算法針對被優化的函數，首先初始化一群隨機粒子(隨機解)，所有的粒子都有一個被優化函數決定的適應度值。每個粒子還有一個速度來決定它們飛行的方向和距離，粒子們追隨當前的最優粒子在解空間中搜索[10]。

尋找最優解的過程通過迭代實現，每次迭代中粒子位置的更新是靠追蹤2個極值來完成，分別是粒子本身找到的最優解，即個體極值，以及整個種群當前找到的最優解，即全局極值。

粒子群算法比遺傳算法規則更為簡單，沒有遺傳算法的交叉(Crossover) 和變異(Mutation) 操作，通過追隨當前搜索到的最優值來尋找全局最優。這種算法以其實現容易、精度高、收斂快等優點引起了學術界的重視，并且在解決實際問題中展示了其優越性。

(8)

(9)

式(8)、式(9)為粒子群算法的核心公式，該算法由以上兩式完成速度和位置的更新，式中kg=1,2,…，G，i=1,2,…，size,r1、r2為0到1的隨機數，c1為局部學習因子，c2為全局學習因子，p和BestS分別表示局部最優解和全局最優解。

對參數的設置是算法中重要的一環，其中包括：1)粒子數的選取，常取20～40，對于比較復雜的問題，也可取100或200。2)最大速度Vmax的設定，該值決定粒子在一個循環中最大的移動距離，通常小于粒子的范圍寬度。較大的Vmax可以保證粒子種群的全局搜索能力，較小的Vmax則可以加強粒子種群的局部搜索能力。3)學習因子c1、c2一般取值2.0，通常c2取值更大些。4)慣性權重w(t)：一個大的慣性權值有利于展開全局尋優，而一個小的慣性權值有利于局部尋優[11]。

PSO算法以流程圖如圖2所示。

2.2 粒子群算法用于溫漂補償

依據式(6)建立算法模型

eΔT2,i=1,2,…,N

(10)

辨識誤差指標取

(11)

J取值越小，說明模型輸出越接近實測數據，此時補償量即為

ΔN=aT+bT2+cT3+dΔT+eΔT2

(12)

利用Matlab中提供的粒子群算法工具箱(PSOt)進行編程，采用上面所述方法對三軸加速度計輸出分別建立溫度補償模型。參考粒子群算法在實際工程中的應用，針對本優化模型，待辨識參數的取值范圍設置為[-1,1]，粒子數取50，共迭代500次，粒子最大速度以及學習因子等參數取工具箱默認值，以此實現該算法模型[12-14]。

3 試驗驗證與結果

試驗平臺主要包括溫箱、電源、工控機、數據采集及處理模塊、上位機測試軟件以及外圍接口電路等，如圖3所示。試驗對象為某型光纖慣組，其光纖陀螺和石英加速度計內部均設有測溫電阻，可實時檢測其內部溫度并與器件輸出一并發至上位機。

3.1 參數辨識過程

由于加速度計的溫度漂移受溫變速率與當前溫度值的影響,為了求取加速度計在全溫條件下的溫度模型,必須采樣不同溫度及不同溫變速率下的加速度計零位漂移[15]。試驗中分別選取溫度點為-40℃、0℃、60℃，且在變溫過程中選擇不同的溫變速率，建立溫度變化模型如圖 4所示。采集在此溫變模型下光纖慣組三軸加速度計的輸出作為樣本集，以粒子群算法辨識溫補參數，并代入樣本數據進行驗證。

3.2 驗證過程

將溫補參數加載到下位機中，并設置下位機程序使其能夠同時輸出加速度計溫補前和溫補后參數。然后分別在溫度點-40℃、-20℃、0℃、20℃、40℃、60℃，采集加速度計輸出。

具體方法是：在溫箱達到設定溫度后，保溫2h使系統達到熱平衡，之后慣組上電并采集1h數據，以模擬加速度計在該溫度環境下的工作狀態。實際上，加速度計溫度會經歷由自發熱導致升溫并逐漸達到溫度穩定的過程。對比溫補前和溫補后加速度計的輸出曲線，并以2個狀態下的零偏穩定性作為參考，驗證本文提出的溫度補償方法的實際效果。

3.3 結果分析

以y軸加速度計為例，分別驗證其在低溫-40℃，常溫20℃以及高溫60℃下的輸出及補償后曲線，試驗中加速度計溫度可通過溫度傳感器實時得到，其溫度變化曲線如圖5所示。

由圖5可以看出，加速度計的工作溫度存在一個緩變過程，溫度的變化將導致輸出的漂移。圖 6～圖 8給出了補償前后加速度計輸出對比曲線，可以發現未經補償前在不同溫度點下開機，加速度計輸出先是表現為一個較大的零偏值，之后在系統溫度上升并最終達到熱平衡的過程中，加速度計輸出減小，輸出曲線上升，并在系統達到熱平衡之后輸出曲線方才趨于平穩。而補償后的曲線被明顯拉平，輸出維持在0附近，可認為在系統啟動至達到熱平衡的過程中輸出保持穩定。

表 1所示為經粒子群算法補償前后加速度計零偏穩定性的計算情況，補償前y軸加速度計的零偏穩定性在0.6mg左右，而經粒子群算法補償之后零偏穩定性不超過0.1mg，最優值接近0.05mg，相較于補償前提升了近1個數量級。同時與最小二乘法得到的補償結果相對比，不難發現粒子群算法結果更優，在一定程度上能夠獲得更高的補償精度。

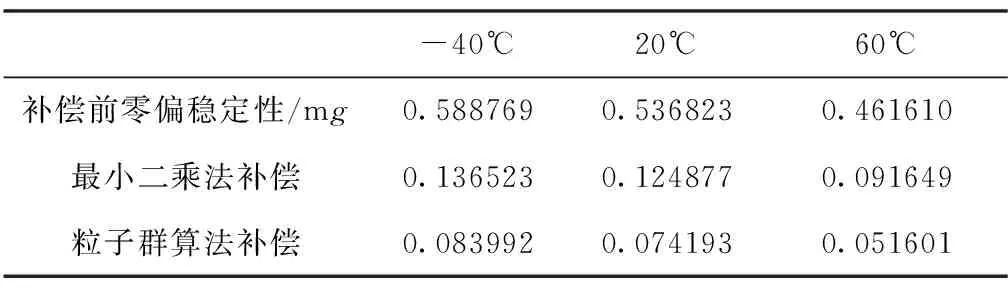
表1 不同溫度下加速度計補償前后零偏穩定性

4 結論

本文針對工程實例中對慣組石英撓性加速度計輸出穩定性(隨溫度變化)的需求開展研究，進行了如下工作：

1)通過分析石英撓性加速度計的溫度特性，提出了一種與溫度、溫度高次項及溫度變化率相關的溫度誤差模型；

2)在溫補參數辨識工具的選擇上，使用了粒子群算法，通過對算法的合理設計及參數的合理設置，實現了對模型參數的準確辨識；

3)搭建了試驗平臺對本文提出的溫度補償方案進行驗證，該補償算法在試驗中表現出良好的補償效果，成功將加速度計零偏穩定性提升近1個數量級，收斂速度快，算法易于實現，可有效提升慣組精度。