基于動力學軌道擬合的LEO衛星軌道預報精度分析

王友存,郭金運,夏要偉,孔巧麗

(山東科技大學 測繪科學與工程學院,山東青島 266590)

0 引 言

低軌衛星在完成對地觀測計劃、數據上下行計劃、軌道維持、機動計劃及激光測距等方面的科學任務時,對于衛星軌道預報有一定的精度要求[1-2]。考慮到低軌衛星星載設備的不穩定性,會出現短時間的信號失鎖,通過對衛星的軌道進行預報,實現了數據中斷處的有效連接[2]。同時在衛星的自主導航系統中需要實時對衛星軌道進行預報[1-2]。此外,基于低軌衛星的星間鏈路增強技術是導航衛星系統常用的技術手段[3],當低軌衛星作為星基監測站時,衛星需要進行軌道預報來完成“廣播星歷”的發布[3-4]。因此低軌衛星的軌道預報是衛星任務順利執行的基本要求。

目前針對低軌衛星的軌道預報主要方法有:基于多項式擬合的方法,通過一組先驗的衛星軌道信息完成對多項式系數的求解[5-6],再利用完整的多項式對衛星軌道進行預報[6]。常用的擬合方法包括拉格朗日插值[6-7]、Neville 插值[8]、切比雪夫多項式擬合[6-8]、最小二乘曲線擬合[8]等。由于LEO衛星運行的軌道高度較低,衛星受到的攝動情況相比中高軌衛星較為復雜[9],這種避免了力學模型的多項式預報方法僅適用于較短弧段(幾分鐘以內)軌道預報[9-10]。基于衛星軌道根數的分析方法,通過對衛星某一時刻的平均軌道根數進行外推的一種預報方法。這種方法通常適用于對衛星軌道精度要求不高的領域,例如空間環境監測[11]和實時跟蹤測量[12]中,軌道的預報精度在幾百米甚至幾千米不等[12]。基于確定性動力學模型的動力學方法,根據已知的衛星軌道作為先驗信息采用動力學擬合方法估計出一組衛星初始歷元下的位置、速度和動力學參數[13],并利用這組衛星的初始信息進行軌道預報[9-10]。相比前兩種方法,這種動力學方法可以對低軌衛星進行較長弧段的軌道預報[14-15],預報的精度較高[9-13],對于低軌衛星具有很好的科學使用價值[13]。

本文針對不同軌道高度的低軌衛星,運用了動力學軌道擬合的方法,對衛星軌道進行預報,并著重分析了不同區間長度的擬合弧段對衛星軌道預報的精度影響。

1 動力學處理策略

1.1 動力學基本方法

低軌衛星在環繞地球飛行的同時,受到各種攝動力的作用影響[16-17],其運動微分方程為[16]

(1)

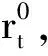
(2)

(3)

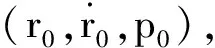
1.2 軌道預報處理策略

考慮到低軌衛星的在運行過程受到多種攝動因素[16],在進行動力學軌道預報的過程中需要考慮到地球的非球形攝動、多體攝動、固體潮、海潮等動力學模型[16-21](如表1所示)。其中待估參數主要包括衛星的六個軌道根數和九個光壓模型參數[18]。

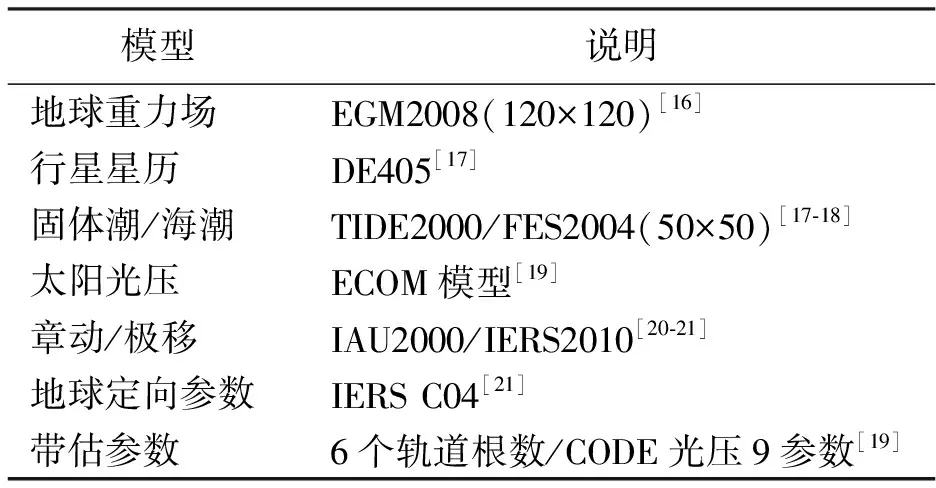
表1 地球物理模型和帶估參數

表2 低軌衛星軌道預報的方案

2 結果與分析

2.1 試驗對象

選取了不同軌道高度的低軌衛星進行了軌道預報處理,文中使用了歐洲定軌中心(CODE)發布的GRACE-A衛星的事后科學軌道[22](ftp://ftp.aiub.unibe.ch/LEO-ORBITS/GRACE/GRACEA/),HY-2A衛星和JASON-2衛星的精密星歷數據取自法國國家空間中心(CNES)[23-25](ftp://cddis.gsfc.nasa.gov/pub/doris/products/orbits/ssa)(軌道說明如表3所示),表4示出了三顆衛星的基本信息。

表3 實驗中選用低軌衛星的先驗軌道

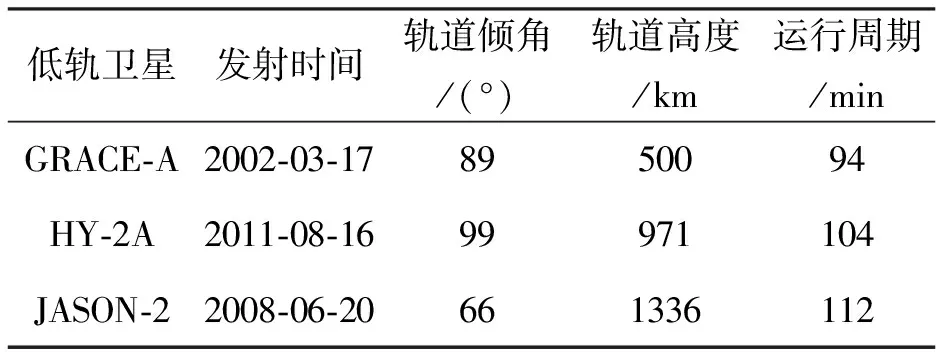
表4 實驗選用的低軌衛星

2.2 不同弧長的擬合結果分析

根據表2的預報方案,利用Bernese 5.2軟件對三顆低軌衛星完成了不同弧段的軌道擬合,并對軌道擬合結果的RMS進行了統計。其中,三顆衛星采用的軌道積分步長均為1 min.

根據表2的方案選取4 h到24 h先驗軌道,進行動力學方法擬合,將擬合結果與衛星的精密星歷作比較,三顆衛星的擬合結果如圖1～圖3所示。可以看出GRACE-A衛星在4 h到24 h弧段的擬合RMS均大于HY-2A衛星和JASON-2衛星,并且隨著弧段的增加,擬合效果出現較大的波動。根據表5給出的RMS平均值的統計結果來看,在4 h的弧段內,HY-2A衛星和JASON-2衛星的擬合結果基本上保持在同一數量級上,在8 h到24 h的弧段內,GRACE-A衛星擬合RMS遠大于其余兩顆衛星,相差的RMS平均值在兩個數量級,HY-2A衛星和JASON-2衛星擬合的結果大致保持在一個相近的水平。

從表5示出的結果來看,選取的擬合弧段不斷增長,三顆衛星擬合結果的RMS明顯變大,并且擬合結果出現較大波動。從整個弧段的擬合結果來看,JASON-2衛星優于HY-2A衛星的結果,而GRACE-A衛星擬合效果最差,擬合結果不穩定。隨著擬合弧段的增加,GRACA-A衛星的擬合結果RMS變化較為明顯,尤其是24 h弧段的擬合RMS其最大值達到了6.72 m.相比之下,HY-2A衛星和JASON-2衛星整個擬合結果較為穩定,均保持在厘米精度。

表5連續兩周不同弧段擬合的RMS平均值m

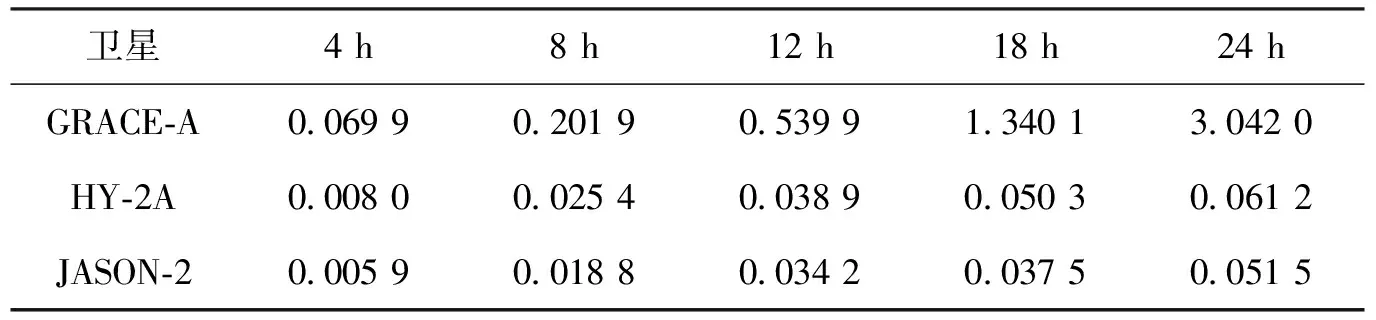
衛星4 h8 h12 h18 h24 h GRACE-A0.069 90.201 90.539 91.340 13.042 0 HY-2A0.008 00.025 40.038 90.050 30.061 2 JASON-20.005 90.018 80.034 20.037 50.051 5

2.3 不同擬合弧長的軌道預報結果分析

采用表2的方案,設置了4 h到24 h的外推弧長進行預報,針對每一個預報的弧段采用了4 h到24 h的擬合弧長進行預報。為了獲取軌道預報的精度信息,文中將三顆衛星的精密星歷作為真值與預報軌道進行比較得到不同弧段內的RMS.如圖4～圖8所示,將連續兩周時間內三顆衛星采用不同弧長擬合進行軌道預報的結果進行了統計。

根據圖4～圖8結果分析,從GRACE-A衛星的預報結果來看,對于預報4 h和8 h等較短弧段的軌道時,宜采用4 h弧段擬合,其中預報4 h弧長的RMS小于3 m,而預報8 h弧長的RMS小于11 m,并且預報結果波動較為平緩。在預報12 h、18 h和24 h的軌道時,采用8 h弧段擬合進行預報結果相對較好。利用8 h擬合弧段在預報18 h的軌道時,預報結果的 RMS最大值達到了89 m,最小值在8 m,預報24 h軌道時其RMS最大值達到了198 m,最小值在13 m.對于GRACE-A衛星而言,對于4 h弧段的預報效果較為理想,長弧段的預報結果波動較為劇烈,精度較差。

對于HY-2A衛星,在預報4 h和8 h的軌道時,宜采用8 h弧段擬合,其中預報4 h弧長的RMS小于2 dm級精度。對于預報12 h及以上的軌道時,利用18 h擬合弧段可以達到較好的預報結果,其中預報24 h弧長的RMS小于2.5 m.從圖8可以看出,整個預報過程較為穩定,相比GRACE-A衛星HY-2A衛星軌道預報結果較好。

對于JASON-2衛星,在預報4 h和8 h的軌道時采用12 h的擬合弧段較為合適,其中預報4 h弧長的RMS小于1 dm.當預報12 h及以上的弧段時宜選取24 h的擬合弧段,其中預報24 h弧長的RMS小于2 m.相比GRACE-A衛星和HY-2A衛星,JASON-2衛星兩周的預報結果較好,波動更為平緩。由此可見,對這三顆低軌衛星的預報結果而言,隨著衛星軌道高度的升高,其預報結果越好,結果較為穩定。

3 結束語

本文通過利用動力學軌道擬合的方法對不同軌道高度的低軌衛星進行了軌道預報,根據上述試驗結果分析,可以得出以下結論:

1) 采用動力學方法對低軌衛星進行擬合的過程中,由于選取的先驗軌道的弧段不同,弧段的擬合效果相差較大。從GRACA-A衛星的擬合結果來看,對于軌道在500 km左右的衛星,擬合結果較差,并且結果不穩定。其中4 h擬合弧段的RMS平均值少于7 cm,對于8 h及以上弧段的擬合效果較差,使用價值不高。對于軌道高度在971 km的HY-2A衛星和軌道高度為1 336 km的JASON-2衛星,全弧段的擬合精度相對較好,結果較為穩定。

2) 從文中這種動力學軌道擬合方法的預報結果來看,GRACE-A衛星4 h軌道的預測結果RMS好于3 m,對24 h軌道的預報結果較差。HY-2A衛星4 h和24 h軌道預報RMS分別優于2 dm和2.5 m,JASON-2衛星的4 h和24 h軌道預報RMS分別優于1 dm和2 m。對于軌道高度在500 km左右的GRACE-A衛星,預報結果在幾米到幾十米不等,預報精度較差,使用價值較低,而相對軌道在971 km的HY-2A衛星和1 336 km的JASON-2衛星而言,軌道的預報精度相對較高,含有較高的使用價值。

3) 考慮到低軌衛星的運行軌道高度不同,不同衛星間的攝動情況也會有所差異,對于軌道高度在400～500 km附近的衛星,其大氣阻力是影響預報結果的主要影響因素,而對于高度保持1 000～1 300 km附近的衛星,受到的大氣影響較少,太陽光壓成為了主導因素,因此可以采取不同的策略進行軌道預報。