PMF-FFT方法在P碼捕獲中的改進及參數設計

袁蔥林,唐小妹,韓春陽,孫廣富

(1.國防科技大學 導航與時空技術工程研究中心,湖南 長沙 410003;2.北京衛星導航中心,北京 100084)

0 引 言

通常,P碼的捕獲是通過C/A碼來引導捕獲的,但由于C/A碼周期短,碼速率低,易被敵方干擾和欺騙,在GPS導航戰與電子對抗的環境下,要求GNSS接收機能夠對P碼進行準確迅速的直接捕獲,確保戰時衛星導航系統的正常使用。 P碼的周期長,碼速率高,若使用傳統的捕獲方法,需要很長的捕獲時間,尤其在高動態、大多普勒頻移下,傳統的偽碼捕獲方法很難實現。 因此P碼捕獲的關鍵在于如何減小捕獲時間以及提高多普勒頻率誤差容忍度[1]。

本文將部分匹配濾波器與FFT結合(以下簡稱PMF-FFT)的算法應用到P碼的捕獲中,利用PMF-FFT算法能夠有效抵抗多普勒頻移引起的相關峰衰減的特性,擴大了頻率搜索范圍,在頻域內進行并行搜索,大大提高了捕獲速度,解決了P碼捕獲的關鍵問題。 同時在此基礎上本文使用了重疊保留法對其進行了改進,利用FFT的卷積特性,在實現接收信號與本地偽碼的子相關處理時,引入并行碼相位搜索機制,進一步縮短了捕獲時間。 本文給出了P碼捕獲實現的流程和原理,并用Matlab進行仿真,綜合考慮各個參數之間的關系,提出了相關參數選取的準則,對各項損耗或增益進行了定量分析,從而為該算法的實際應用奠定了堅實的理論基礎。

1 PMF-FFT算法基本原理與信號模型

1.1 基于PMF-FFT的捕獲算法

基于PMF-FFT方法的捕獲流程為[2]:將長為M的接收信號去除載波后,等分成P段,進入P個部分匹配濾波器進行相關匹配,匹配濾波器中裝載長為M的復制碼。 每個相關積分單元對連續的X個采樣點做相關運算,M=PX.對于每一段內位于同一位置的相關積分值進行N點FFT(N>P),若在整個二維空間中出現的最大值超過門限,則判定為捕獲成功,否則將信號移位X點,繼續進行搜索。捕獲原理框圖如圖1所示。

考慮到導航電文比特翻轉問題,相干積分時間不宜過長,可使用非相干累加方法進一步提高信噪比。

1.2 重疊保留法在PMF-FFT算法中的應用

重疊保留法在數字信號處理中,是一種以循環卷積實現線性卷積的快速算法,當兩條序列長度相差很大時,通過將長序列分段重疊,與短序列分別作循環卷積,保留有效值,拼接以得到最終的線性卷積結果。

在使用PMF-FFT方法進行子相關處理時,使用的是串行搜索碼相位的方法,搜索效率較低,若在每個子相關器中使用重疊保留法進行計算,將大大提高接收信號與本地偽碼的相關運算速度。具體應用為:將接收信號分段,每段長為2X,重疊部分長為X,本地偽碼分為P段,存儲在長度為2X的部分匹配濾波器中,其中前X點為偽碼采樣點,后X點為零填充部分,將匹配濾波器中的系數取共軛傅里葉變換后,再與接收信號的傅里葉變換直接相乘,經過IFFT變換,僅保留前X點有效相關值[3]。在獲得P段長為X的相關值后,對處于同一個碼相位的分段相干累加結果進行N點FFT變換,得到該碼相位下對應的多普勒分布,在本次搜索的X個采樣點中取FFT輸出幅值的最大值進行門限判別,若大于門限則認為捕獲成功,若未超過門限則衛星信號向前移位X,再次搜索。搜索判決流程如下:

2 改進后算法性能評估

2.1 信號模型

設接收的信號為

r(t)=Ad(t+τ)C(t+τ)cos[2π(f0+fd)

(t+τ)+φ]+n(t).

(1)

式中：τ為相對本地信號的延遲;f0為載波頻率;fd為多普勒頻移;n(t)為高斯白噪聲。

經過下變頻和采樣后,第n個部分匹配濾波器輸出為

(2)

式中：M為接收信號長度；P為部分匹配濾波器數目；X為部分匹配濾波器長度即單個匹配濾波器進行相關運算的采樣點數；Ts為采樣間隔,與上節中PMF-FFT算法中的參數含義一致。

對P個匹配濾波器的輸出進行N點FFT運算,得到FFT輸出幅度響應為

(3)

將幅值歸一化后得到:

(4)

可將其分成兩部分來看,即

G(fd,k)=G1(fd)G2(fd,k)，

(5)

其中:

(6)

為部分匹配濾波器中進行相關累積引起頻率響應；

(7)

為FFT運算對輸出幅度造成的影響。

2.2 系統整體損耗來源分析

2.2.1 時頻相關積累功率損耗

由上節對信號建模歸一化FFT輸出幅值分析可知,功率損耗來源于兩部分,第一部分為時域相關積分引起的多普勒損耗[4]:

(8)

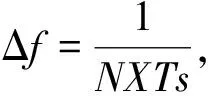
(9)

則相關積分后信號的等效信噪比為

CNR·X·P·Ts.

(10)

2.2.2 包絡檢波損耗

在實際接收機中,需要使用平方律檢波或包絡檢波方法合并I、Q支路信號以消除電文比特翻轉的影響,而采用這類檢波器會引入檢波損耗。包絡檢波損耗的經驗公式可表示為[5]

(11)

則采用包絡檢波器后的信噪比為

(12)

2.2.3 非相干積累功率損耗

為了提高被檢信號的信噪比,接收機通常需要對接收信號進行非相干積分,雖然非相干積分中的積分運算能增強信噪比,但積分之前的平方運算會引入平方損耗LSQ,因此信噪比并不隨非相干累積次數增加而線性增加。

非相干積分增益Gnc的計算公式為[6]

Gnc=10lgNnc-LSQ.

(13)

式中，Nnc為非相干積分次數。

圖3示出了不同非相干積分前信噪比條件下的平方損耗經驗值[7],計算推導過程可參考原書附錄,該圖表明,平方運算對強度越弱的信號會造成越大的平方損耗。

2.3 改進前后搜索X個采樣點的計算量對比

對于傳統的PMF-FFT算法,一個部分匹配濾波器長為X,需要使用串行搜索的方式對X個采樣點進行相關累加,得到一個采樣點的相關值需要進行X次乘法與X-1次加法,因此X個采樣點需要X2次乘法與X·(X-1)次加法。

對于改進的PMF-FFT方法,其存在一半無效相關結果,因而需要將部分匹配濾波器長度拓展到2X,以得到X個采樣點的有效值。

對2X個采樣點進行并行搜索,需要進行兩次FFT操作以及一次IFFT操作。

一次2X點FFT需要(2X)lb2X=2X(1+lbX)次復數加法運算,以及0.5(2X)lb2X=X(1+lbX)次復數乘法運算。一次復數加法相當于兩次加法,一次復數乘相當于4次乘法和3次加法,于是2X個采樣點并行搜索總運算次數為:4X(1+lbX)次乘法和10X(1+lbX)次加法[7]。表1示出了改進前后的PMF-FFT方法搜索X個采樣點的乘法、加法運算量對比。

表1 相關累加運算量比較

由表1可知,使用FFT在頻域內實現時域相關運算可以大大降低運算量,并隨搜索長度的增加,并行搜索的優勢越明顯,代價僅為一倍長度的匹配濾波器長度拓展,通過少量的存儲資源消耗換來計算量上的大大減少,因此該改進方法具有較大應用價值。下節將通過matlab仿真,確定在該改進方法中的最優參數組合選取。

3 捕獲參數優化設計

3.1 仿真背景

本節主要對P碼捕獲的算法性能進行了仿真分析。仿真條件為: 10.23 MHz的P碼碼率,采樣率為20.46 MHz,在載噪比為35 dB·Hz,多普勒頻偏為6 000 Hz條件下,滿足虛警概率為10-6時,捕獲概率≥90%的性能指標的最優參數設計, 包括部分匹配濾波器長度2X(其中前X點為本地偽碼,后X點為零填充),分段數(即濾波器個數)P,非相干累加次數q等,搜索滿足約束條件、性能指標下,使總運算時間最短的參數組合。

1) 約束條件

2) 性能指標

由捕獲概率和虛警概率計算得到等效判決信噪比D0:

=[erfc-1(2Pf)-erfc-1(2Pd)]2.

(14)

將Pd=90%,Pf=10-6代入式(14),可得到等效判決信噪比D0=12.60 dB.

3.2 仿真結果

本文對1～10 ms的相干積分總時間(M·fs),0.001～0.04 ms分段相干積分時間(X·fs)在q次非相干累加后,達到等效判決信噪比的最小總運算時間進行了仿真,為使其位置更加明顯,在圖中以倒數形式展現,峰值所在位置即為該條件下的最優參數選擇,結果如下:

計算機配置為Intel(R) Pentium(R) CPU G2020處理器,主頻2.90 GHz,4 GB內存,64位Win7操作系統。為更好地說明不同參數組合設計會如何影響總運算時間,特地選取了幾組具有代表性的參數來進行說明。

表2為該改進算法在不同總相干積分時間下,選擇不同分段相干積分時間的平均搜索時間(非相干累加次數q=1)。

然后進一步確認在此參數下達到等效判決信噪比的最小非相干累加次數q.如圖5(a)所示,不同的分段相關積分時長在不同的總相干積分時間下,經過包絡檢波后的信噪比也各不相同。因此導致其非相干累加的平方損耗和累加次數也不相同。圖5(b)中的橫線為滿足捕獲性能指標的等效判決信噪比D0,在不同分段相干積分時間下,選取最接近D0的非相干累加次數即可滿足性能指標,同時使總運算時間最短。

表2 不同積分時長下改進PMF-FFT算法的平均搜索時間

不同的分段相干積分時間使得單次PMF-FFT算法的平均時間不同,而分段積分時間不同導致的信噪比和非相干累加次數的不同,將導致總運算時長的差異。圖6示出在不同的總相干積分時長下,不同分段相干積分時間達到等效判決信噪比的總運算時間。

如圖6所示,若選擇總相干積分時長為10 ms時,應當選取分段相干積分時間為0.039 ms,此時總運算時長為0.287 1 s,非相干累加次數為1,即無需進行非相干累加,單次PMF-FFT算法的運算已能達到等效判決信噪比;若選擇總相干積分時間為4 ms,則應當選取分段相干積分時間為0.25 ms,此時非相干累加次數為4次。

由以上結論可以得出,在35 dBHz載噪比,600 0 Hz的多普勒頻率偏移條件下,最優參數組合選取如表3所示。

上述優化設計結果為總相干積分時長確定后,分段相干積分時長與相干累加次數的最優選擇,是滿足“達到等效判決信噪比條件下總運算時間最少”準則的結果。接收機根據自身硬件條件、資源使用情況,以及其他P碼捕獲算法(如XFAST算法)相結合后的參數設計需求,選擇合適的總相干積分時間,在表3中可找到該時間下對應的最優參數設計組合。若不考慮其他算法的性能要求,選用3 ms作為總相干積分時長、0.023 ms為分段相干積分時長、進行5次非相干累加,可使總運算時間最短。總體來說,對于不同的總相干積分時間,分段相干積分時長選在0.02～0.04 ms之間較佳。

表3 不同總積分時長下最優參數選取組合

4 結束語

本文基于PMF-FFT捕獲算法模型,對該算法的原理和特性進行了詳細的分析,并通過建立數學模型,精確地分析了捕獲流程中,整個系統的損耗來源,包括多普勒頻偏造成的相干積分損耗、最大頻率偏差造成的FFT模塊最大扇貝損失、包絡檢波損耗、非相干積分中的平方損耗等,并對該算法在P碼捕獲中的應用做出了改進。通過Matlab仿真,得到了載噪比為35 dB·Hz,多普勒頻偏為6 000 Hz條件下,滿足P碼捕獲性能指標并使得總運算時間最小的最優參數組合設計方案,為該算法的系統參數設計提供了理論依據,具有一定研究價值。