GNSS/INS組合的鐵路軌道三維坐標快速精密測量

周禹昆,陳起金

(武漢大學 衛星導航定位技術研究中心,湖北 武漢430079)

0 引 言

隨著我國鐵路營運里程的大幅增長,既有線的維護、監測和升級任務不斷加重。既有線鐵路中線位置三維坐標的精密測量是線路線型恢復和在旁新建線路的基礎,也是既有線提速和升級的重要技術保障。同時,由于鐵路的運營任務異常繁忙,線路檢測和測量的“天窗”時間不斷縮短。因此,快速獲取厘米級鐵路軌道中線坐標,對于既有線的監測、改造和維護具有重要意義和實用價值[1-3]。對于既有線的測量來說,現有的光學或者其他測量手段難以兼顧測量精度和效率,需要一種全新的鐵路快速精密測量方法。研究我國鐵路的快速精密測量,對于進行高效高精度的鐵路建設和軌道監測來說已經成為十分迫切和重要的課題。

現階段既有線中線測量主要是以傳統大地測量手段完成,包括全站儀和GNSS載波相位差分技術(RTK)。以全站儀為核心的測量手段,通過高精度全站儀在軌道控制網下設站,測量擺放于鋼軌或軌檢小車上棱鏡的坐標,進而采集軌道中線的三維位置,該方法完全依賴控制網,要求棱鏡與全站儀通視,測量效率很低。同時,大部分有砟既有線旁邊并無密集的控制網,難以滿足全站儀測量要求。部分學者嘗試利用GNSS RTK進行軌道中線的快速測量,具體參考文獻[4-6]。但是RTK容易受鐵路復雜測量環境的影響,衛星信號易被干擾、遮擋,影響定位結果的可靠性和可用性,適用性很低。根據以上情況,嘗試利用GNSS/INS組合導航系統的方法來實現高精度、高效率、高穩定性的鐵路軌道三維位置測量。

本文首先闡述基于GNSS/INS組合導航系統的高精度鐵路軌道絕對測量的基本方案和相應算法;然后以鄭徐高鐵實測數據為例,評估本方案測量的精度。

1 GNSS/INS組合導航測量鐵路軌道基本方案

慣性測量單元(IMU)感知載體(軌檢小車)的運動狀態,對三軸比力和角速度測量值進行機械編排運算,獲取載體的位置、速度和姿態信息。由于慣性器件輸出信息噪聲的影響,慣性導航系統自主推算的位置、速度和姿態的誤差會不斷積累下來,嚴重影響到測量的準確性。因此,這里需要使用GNSS信息的輔助來抑制慣導系統誤差的積累。

GNSS的定位精度決定了GNSS/INS組合導航系統的絕對測量精度,動態條件下,衛星事后的載波相位差分技術(PPK)可以在短時間內達到厘米級的定位精度,能夠滿足鐵路軌道絕對測量的要求。當衛星信號受外界遮擋影響時,利用IMU系統短期穩定性好的特點可以自主推算出高精度三維坐標信息修正衛星定位結果。

GNSS/INS組合導航系統結合了慣性測量單元和衛星導航系統的優點,一方面利用慣性測量單元輸出的慣性量測信息具有出色的自主性,提高定位結果對外界干擾的適應性,在短時間內即使無衛星信號也可保持定位結果的連續性;另一方面利用GNSS高精度的絕對定位結果來抑制INS的誤差積累。兩者的誤差傳播性能是互補的,INS系統長期穩定性差,但是短期穩定性好,GNSS導航系統正好相反,GNSS/INS系統很好將兩者結合起來[7-9]。整個測量方案利用GNSS信息輔助抑制慣導的誤差積累,同時通過非完整性約束來和反向平滑算法來進一步提高導航定位的精度。使其在較長時間內穩定輸出高精度的量測信息,從而實現鐵路軌道的三維位置坐標測量。

由于GNSS/INS系統定位解算結果為被測軌道位置的大地坐標,參照鐵路工程衛星定位測量規范,可以將GNSS/INS組合導航系統解算出的高精度大地坐標轉換到軌道施工獨立坐標系下,從而應用于鐵路軌道的絕對測量。圖1示出了整個方案的詳細流程。

2 數據融合算法

針對鐵路軌道精密測量這一特殊應用,本文在傳統的組合導航算法中加入了非完整性約束和反向平滑算法,用以提高GNSS/INS系統的測量精度,來適應鐵路的測試要求。同時,本文根據鐵路工程衛星定位測量規范,將量測坐標轉換到當地鐵路施工坐標系。

2.1 卡爾曼濾波模型

卡爾曼濾波作為一種重要的最優估計理論已經廣泛應用于組合導航系統,實現最優估計。本文設計了21維狀態量的卡爾曼濾波器。其中,慣性導航推算的位置、速度、姿態誤差在導航坐標系(n系)下表示,姿態誤差采用Phi角模型[10-11]。詳細的慣導機械編排算法可參考文獻[12]。

在組合導航解算過程中,慣性傳感器的殘余誤差是影響測量精度的重要誤差源,需要在濾波器中進行在線的估計和補償。由于IMU誤差隨時間變化緩慢,將上述誤差建模為一階高斯-馬爾科夫過程,增廣到系統狀態量中在線估計。卡爾曼濾波狀態量包括位置、速度、姿態誤差和慣性傳感器誤差。具體表示為

x(t)=

(1)

式中:δrn為慣導在n系下的位置誤差;δvn為在n系下的速度誤差;φ為慣導姿態誤差;b,s分別為IMU陀螺和加速度計的零偏誤差和比例因子誤差。

位置、速度和姿態的誤差微分方程可以表示為

(2)

卡爾曼濾波器的狀態方程可以表示為

(3)

式中:F為狀態轉移矩陣;G為系統噪聲矩陣;x為系統狀態量;w為驅動白噪聲。

GNSS的位置信息在卡爾曼濾波器中作為觀測信息進行更新,GNSS位置和慣導機械編排推算得到的位置差值作為濾波器的離散觀測向量,觀測方程為

(4)

2.2 反向平滑模型

為了充分地利用當前和前后歷元所有的觀測量,進一步提高鐵路測量的精度,在GNSS/INS 組合導航數據后處理中加入了反向平滑算法。本文采用的反向平滑算法為R-T-S平滑算法。R-T-S算法是一種典型的固定區間平滑線性算法,能夠利用過去、當前和未來歷元的觀測信息計算出比卡爾曼濾波更準確的狀態量估計值[13]。算法具體為

(5)

式中:Ak為增益平滑矩陣;Φ為狀態轉移矩陣;P為狀態誤差陣;N為測量歷元總數。

2.3 坐標轉換

GNSS/INS組合導航輸出的結果為CGCS2000/WGS-84坐標系統的大地坐標,需要轉換為軌道獨立坐標系下的平面坐標和高程,具體步驟包括平面坐標變換和高程異常改正。

平面坐標采用直接投影法計算施工坐標。直接投影法采用工程橢球作為參考橢球,將GNSS/INS組合導航解算出的WGS-84結果直接投影到工程橢球相切的高斯平面上,進行施工平面坐標的計算[14]。

在施工坐標計算前,需要將大地坐標轉為高斯平面坐標,完成高斯平面投影的計算,具體算法參考文獻[15]。施工坐標計算具體為:

xs=x0+Δx·cosε-Δy·sinε,

ys=y0+Δx·sinε+Δy·cosε,

ε=αs-αg,

(6)

式中:x0和y0為施工坐標系起算坐標;αs為施工坐標軸在施工坐標系中的方位角;αg為施工坐標軸在高斯平面直角坐標系中的方位角。

GNSS/INS輸出的大地高程轉換為獨立坐標系下的正常高,需改正高程異常。本方法將測區似大地水準面視為一個曲面,通過工程設計文件的控制點GPS坐標和水準高來擬合出似大地水準面,內插出各實測點的高程異常,對實測大地高進行改正[16]。高程擬合計算具體為

(7)

式中:

(8)

其中：B和L為給定控制點的大地坐標；B0和L0為大地坐標的平均值；H和h分別為給定控制點的大地高和水準高；ζ為高程異常。

3 結果及數據分析

3.1 實驗數據采集及設備性能指標

為評估GNSS/INS軌道測量系統的整體性能及測量精度,在徐鄭高鐵客運專線鄭州段進行軌道測量試驗。在試驗線路使用軌檢小車搭載GNSS/INS組合導航系統和軌距、里程計傳感器采集了11 km數據。測試時,被測軌道剛剛完成長軌精調,覆蓋直線段、緩和曲線段和圓曲線段,采集現場如圖2所示。所用慣導設備為武漢邁普時空導航科技有限公司的POS830系統,其陀螺零偏為0.01 deg/h,加速度計零偏為25 mGal,內置GNSS板卡為NovAtel OEMV-2.

3.2 實驗結果分析

測試期間徐鄭高鐵剛剛完成軌道長軌精調,鋼軌的實際位置與設計位置差異不大于幾個毫米。在數據分析中,以鋼軌的設計位置為參考,評估GNSS/INS的實測精度。圖3示出了測試區段解算結果和參考真值在水平方向和高程方向的差值。從圖中可以看出,GNSS/INS組合導航系統進行鐵路軌道絕對測量在水平方向的最大誤差小于2.0 cm,在高程方向的最大誤差小于5.0 cm,高程方向精度低于平面精度。同時,位置誤差分布比較均勻,總體系統表現穩定。表1的統計數值說明測量軌道位置誤差均方根在水平和高程方向上分別優于0.6 cm和1.5 cm,能夠滿足設計院對既有線中線測量和設計線型恢復的測量精度要求。

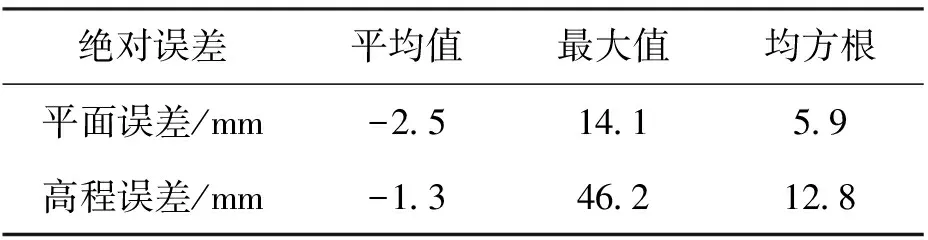
表1 誤差統計結果

4 結束語

本文嘗試了一種基于GNSS/INS組合導航系統的鐵路軌道快速測量方法,采用軌檢小車移動平臺搭載慣性測量單元來獲取高頻率、高穩定性的位置、速度和姿態信息,建立了高精度組合導航算法模型、軌道測量坐標計算模型和科學的精度評估方法。本方法在施工作業的過程中,具有很好的穩定性,不依賴大量的施工控制網坐標,可以在20 m/s的速度下完成軌道的高精度絕對測量任務。在徐鄭高鐵軌道測量數據表明,軌道絕對測量平面坐標精度優于6 mm(RMS),高程坐標精度優于15 mm(RMS),可以滿足絕對測量精度需求。因此,本文提出的通過GNSS/INS組合導航系統測量高鐵軌道絕對位置坐標的方法有很大的潛力和應用前景。

下一步的工作將對算法進一步優化,嘗試使用低精度、低成本的微機電系統(MEMS)代替高精度的慣導設備來實現慣性精密工程測量在鐵路軌道絕對測量上的應用,充分利用和發掘慣性測量單元對運動的感知和測量能力。

致謝：感謝中鐵第四勘察設計院彭先寶教高提供測試場地和設計線型數據，感謝武漢邁普時空導航科技有限公司提供高精度組合導航系統。