基于波形特征的外輻射源雷達雜波抑制算法

趙志欣，周新華，朱斯航，洪 升，王玉皞

(南昌大學信息工程學院，江西南昌330031)

0 引 言

目前的數字廣播電視信號(如數字音頻廣播(digital audio broadcasting,DAB)、數字視頻廣播(digital video broadcasting-terrestrial,DVB-T)、數字地面多媒體廣播(digital terrestrial multimedia broadcasting,DTMB)和數字調幅(digital radio mondiale,DRM)廣播等)大都采用正交頻分復用(orthogonal frequency division multiplexing,OFDM)技術,因其類圖釘型的波形模糊特性和抗頻率選擇性衰落能力為雷達提供了良好的照射源,可便利地組建OFDM波形外輻射源雷達[1-6]。此雷達具有以下主要優勢:①生存能力強、隱蔽性好;②輻射源分布廣泛,較小地受到敵方的影響,抗干擾能力強;③雷達系統簡單、尺寸小、方便部署;④不需要頻率分配,可以部署在其他雷達不能部署的地方。基于上述優點,OFDM波形外輻射源雷達重新受到人們的重視并逐漸成為研究的熱點[7-9]。

外輻射源雷達信號處理通常采用相干處理技術,在接收系統中必須包括參考通道和監測通道,分別用來接收參考信號和目標回波信號。監測通道除了接收目標回波信號外,還不可避免地存在直達波信號和多徑回波信號,使得匹配濾波后得到的距離-多普勒(range-Doppler,RD)譜中,目標信號被直達波和多徑回波(統稱為多徑雜波)所掩蓋。直達波和多徑回波的抑制是外輻射源雷達信號處理需要解決的關鍵問題。一些參考文獻利用最小均方(least mean square,LMS)算法、歸一化最小均方(normalized least mean square,NLMS)算法和遞歸最小二乘(recursive least square,RLS)算法等自適應濾波算法對多徑雜波進行抑制,然而這些算法都存在濾波器階數較多或迭代收斂性的問題[10-14]。同時,在實際應用中多徑雜波的條數往往不清楚,常規時域自適應濾波算法的濾波器階數只能粗略估計,這也將影響雜波抑制的效果。針對上述問題,基于OFDM波形的特點,本文提出了分載波自適應濾波算法,將時域信號變換到載波域,利用同一載頻下直達波和多徑回波的相關性,在每個有效子載波上分別進行自適應濾波得到目標回波信號。與常規時域自適應濾波算法相比,分載波自適應濾波算法的濾波器階數恒為1,降低了計算復雜度,便于信號實時處理,提高了自適應濾波性能。

DRM廣播作為世界范圍內唯一的高頻段非專利數字廣播,其同樣采用OFDM調制方式,在世界范圍內覆蓋廣泛,為高頻段外輻射源雷達較為理想的照射源[15-17]。不失一般性,本文將以DRM廣播為例來研究OFDM波形外輻射源雷達分載波自適應濾波算法。首先，結合DRM介紹OFDM廣播信號的特點和外輻射源雷達接收信號模型；然后，從理論上分析分載波自適應濾波算法的原理；最后，利用仿真數據和實測數據分析比較常規時域自適應算法和分載波自適應濾波算法的性能差異。

1 信號建模

1.1 DRM廣播結構

DRM廣播是針對30 MHz以下長波、中波、短波波段的新一代數字廣播。它采用OFDM技術,可以有效對抗多徑干擾產生的頻率選擇性衰落、多普勒頻率漂移等惡劣影響。OFDM是一種多載波調制技術,即同時用多個正交的子載波來傳遞數據流。實際中一般采用對數據流進行離散傅里葉逆變換(inverse discrete Fourier transform,IDFT)來實現,當子載波數不是2的冪次方時通常采用兩邊補零做IDFT的方式,其中攜帶數據的子載波為有效子載波。這些同時傳遞的數據流組成了OFDM符號的有用部分,再選取符號尾部一段作為循環前綴(cyclic prefix,CP)插入相鄰符號間,即可構成一個完整的OFDM符號。以模式B為例,每個OFDM符號的有用部分涉及IDFT的點數為Nu=256,但是有效子載波的個數Ns=207。多個OFDM符號構成一個傳輸幀,OFDM信號一般以幀為單位傳輸。DRM標準中定義了5種(A～E)不同的傳播模式,分別適用于不同的傳輸環境[18]。綜上所述,DRM基帶信號可以表示為

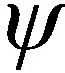
(1)

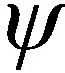
(2)

式中,k為子載波序號;l為符號序號;r為傳輸幀序號;S為每幀的OFDM符號個數;kmax和kmin分別是k的上下限;Ts為一個完整OFDM符號周期;Tu為OFDM符號有用部分持續時間,其倒數1/Tu即為子載波頻率間隔;Tg為OFDM符號保護時間間隔;Cr,l,k為第r幀中第l個符號內第k個子載波的復調制碼元歸一化值。

1.2 雷達接收信號時域模型

外輻射源雷達的參考通道用于接收發射站發射的直達波信號,通過對參考通道提純保證參考信號的純凈性[19]。而監測通道接收到的信號包括直達波、多徑回波和目標回波信號等。監測通道回波的時域信號模型[20]可以表示為

τp)+

(3)

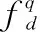
2 分載波自適應濾波算法分析

前文給出了監測通道回波的時域信號模型,本節將分析給出相應的載波域信號模型。將監測通道時域信號按OFDM完整符號劃分、去除保護間隔,并對每個OFDM符號有用數據部分進行離散傅里葉變換(discrete Fourier transform,DFT),即將數據由時域轉換到了載波域;然后僅保留有效子載波上不同OFDM符號間攜帶的數據,便得到有效子載波域的監測通道信號,可以表示為

(4)

式中,Yl,k為監測通道信號有效子載波k第l個符號對應的載波域信號采樣值;Yl為監測通道信號符號l對應的不同子載波組成的載波域信號向量,可以表示為[Yl,1，…，Yl,k，…，Yl,Ns];Yk為監測通道信號有效子載波k對應的不同OFDM符號組成的載波域信號向量,可以表示為[Y1,k，…，Yl,k，…，YL,k]T;L和Ns分別表示OFDM符號的個數和有效子載波的個數。

下面結合監測通道的時域信號模型和信道傳輸模型,對Yl中直達波、多徑回波、目標回波的成分如下:

(1)分析Yl中直達波部分的表達式

假設直達波的信道傳輸函數為Adδ(t),根據OFDM技術的原理,發射信號的第l個符號的時域采樣dl(t)可以表示為

:T0:lTs

(5)

式中，Cl,k為有效子載波k第l個符號所對應的復調制碼元歸一化值。

Yl中直達波部分的表達式為

DFT[dl(t)?Adδ(t)]=DFT[Addl(t)]=

Ad[Cl,1，…，Cl,k，…，Cl,Ns]

(6)

可以進一步得到Yl,k中直達波對應部分表示為AdCl,k。

(2)分析Yl中多徑回波的表達式

以第p個多徑回波為例,假設多徑回波的信道傳輸函數為Apδ(t-τp)。Yl中第p個多徑回波對應部分可以表示為

DFT[dl(t)?Apδ(t-τp)]=DFT[Apdl(t-τp)]=

Ap[e-jω1τpCl,1，…，e-jωkτpCl,k，…，e-jωNsτpCl,Ns]

(7)

同理,可以進一步得到Yl,k中第p個多徑回波對應部分為Ape-jωkτpCl,k。

(3)分析Yl中目標回波的表達式

以第q個目標回波為例,Yl中第q個目標回波對應部分可以表示為

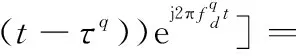
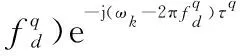
(8)

式中，Dl(ωk)=DFT(dl(t))=[Cl,1，…，Cl,k，…，Cl,Ns]。

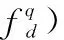
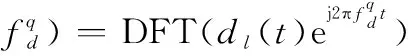
(9)

因為在一個符號內的多普勒頻移的相位旋度非常小,幾乎可以忽略不計,即可近似得到:

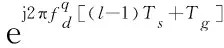
(10)

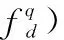
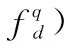
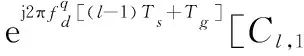
(11)

結合式(8)和式(11),Yl中第q個目標回波對應部分可最終表示為

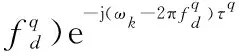
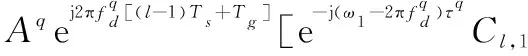
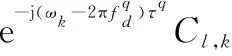
(12)

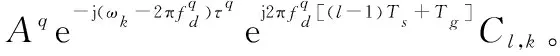
綜上所述,Yl,k的表達式可以寫為

(13)

式中,Nl,k為有效子載波k第l個符號的載波域噪聲。

接著將有效子載波k對應的L個Yl,k組成向量,Yk的表達式可以寫為

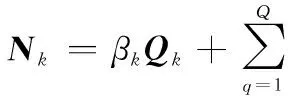
(14)

式中

Qk=[C1,k，…，Cl,k，…，CL,k]T

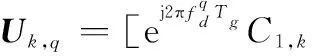
Nk=[N1,k，…，Nl,k，…，NL,k]T

綜上對比式(14)和式(3)可見:相比于時域信號s(t),載波域信號Yk成分由4項減為3項,即由于直達波和多徑回波部分在時域上僅時延不同,故在載波域上可合并成一項(且與Qk完全相關),而目標回波部分與Uk,q完全相關,且Uk,q和Qk幾乎不相關。因此可以利用自適應濾波器分別在有效子載波上進行自適應濾波。以Qk為參考信號,通過自適應濾波器估算系數βk,再將其從Yk中減掉,即為目標回波和噪聲項。根據自適應濾波過程的代價函數不同,可采用分載波遞歸最小二乘(recursive least square by subcarrier,RLS-C)和分載波歸一化最小均方(normalized least mean square by subcarrier,NLMS-C)算法。下面分別給出RLS-C和NLMS-C算法進行自適應濾波的具體步驟。

(1) RLS-C算法

步驟1初始化,令Wk(0)=0,Pk(0)=δ-1I,其中δ是一個很小的值,I是一個常數。

步驟2更新:n=1,2,…,L

(15)

(16)

(17)

(18)

式中,λ是遺忘因子;kk(n)是增益因子;Wk(n)是第k個有效子載波進行自適應濾波的濾波器系數;ek(n)是第k個有效子載波行自適應濾波的濾波器輸出,即為包含目標信息的載波域信號。

(2) NLMS-C算法

步驟1初始化,令Wk(0)=0。

步驟2更新:n=1,2,…,L

(19)

(20)

(21)

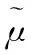
經過上述的自適應濾波處理,對濾除直達波和多徑雜波的監測通道的載波域信號分符號進行補零,然后做IDFT變換回時域,將新的時域監測通道信號與對應的時域參考通道信號進行匹配濾波,即可得到濾除多徑雜波后目標的相關信息。整個分載波自適應濾波算法流程圖如圖1所示。

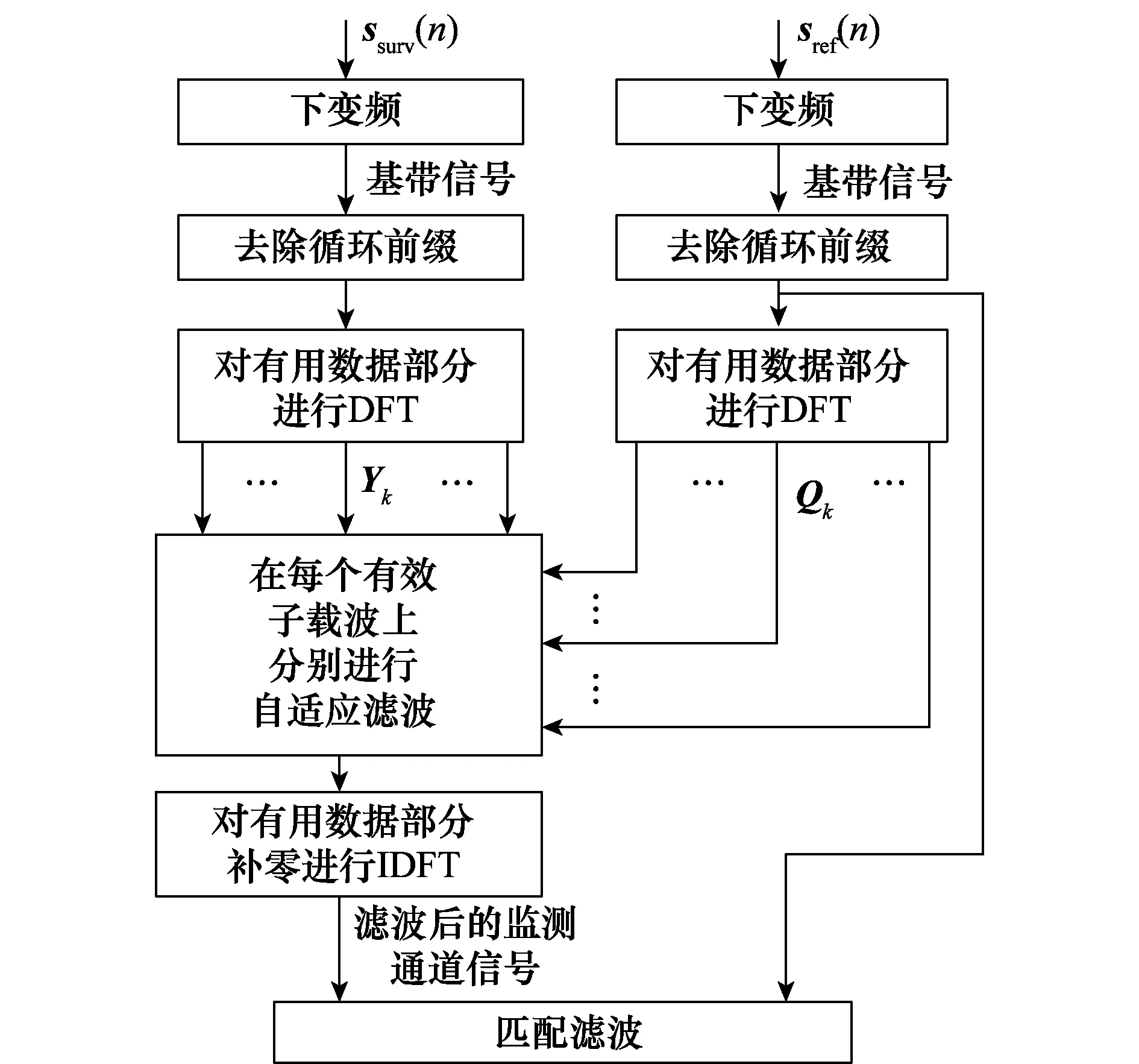
圖1 分載波自適應濾波算法流程圖Fig.1 Flow chart of subcarrier adaptive filtering algorithm

下面分析上述兩種算法實現過程中的算法復雜度。兩種算法都要進行DFT、IDFT和自適應濾波過程。如果利用傅里葉蝶形快速算法對監測通道信號L個符號分別作DFT和IDFT,對參考通道的L個符號分別作DFT,一共需要(3/2)NuLlog2Nu次復乘計算。每個有效子載波上進行自適應濾波的迭代次數是L,有效子載波的個數是Ns,兩種算法自適應濾波過程的迭代次數都是NsL,但是這兩種算法自適應濾波過程的復乘計算量不同。RLS-C算法每次迭代需要8次復乘計算,整個自適應濾波過程進行的復乘次數為8NsL,而NLMS-C每次迭代需要4次復乘計算,整個自適應濾波過程進行的復乘次數為4NsL。所以,RLS-C和NLMS-C算法的總復乘次數分別為(3/2)NuLlog2Nu+8NsL和(3/2)NuLlog2Nu+4NsL。同時,易知RLS和NLMS算法的總復乘次數分別為(4M2+4M)N和(3M+1)N,其中M是自適應濾波器的階數,N是監測信號和參考信號的時域采樣點數。具體推導可參考文獻[21]。表1列出了上述4種算法的迭代次數和計算復雜度。

表1 4種算法的參數和計算復雜度

自適應濾波算法的計算復雜度與自適應濾波器階數和迭代次數有關,常規時域自適應濾波算法的計算復雜度隨著自適應濾波器階數的增加而增加,而分載波自適應濾波算法的自適應濾波器階數固定為1,兩類算法迭代次數相當。雖然分載波自適應濾波算法要對監測通道信號和參考通道信號進行DFT、IDFT會帶來一些計算量,但是相比于常規時域自適應濾波器階數增加所帶來的計算量,上述過程顯然小的多。因此,分載波自適應濾波算法能夠降低計算復雜度。

3 仿真與實測數據結果分析

3.1 仿真數據結果分析

圖2是雜波抑制前仿真的監測通道信號與參考通道信號進行匹配濾波得到的RD譜圖。從圖中可見零頻附近存在大量的多徑雜波,目標完全被多徑雜波所掩蓋。圖3和圖4分別是利用RLS和RLS-C算法對仿真的監測通道信號進行雜波抑制后,與仿真的參考通道信號進行匹配濾波得到的RD譜圖。圖5是這兩種算法處理后目標距離元的截面圖。相比于RLS算法,RLS-C算法的自適應濾波器階數為1,收斂速度快且有較小的輸出誤差,雜波抑制效果更好,目標的信噪比提升了10 dB左右。圖6和圖7分別是利用NLMS和NLMS-C算法對仿真的監測通道信號進行雜波抑制后,與仿真的參考通道信號進行匹配濾波得到的RD譜圖。圖8是這兩種算法處理后目標距離元的截面圖。同理,NLMS-C算法的自適應濾波器階數也為1,收斂速度比NLMS算法快,輸出誤差小,雜波抑制效果好,目標的信噪比提升了5 dB左右。結合上述結果可知,這4種算法都能夠抑制多徑雜波,使目標凸顯出來。然而,RLS算法的復乘次數為1.2×108,RLS-C算法的復乘次數為2.4×106,NLMS算法的復乘次數為6.5×106,NLMS-C算法的復乘次數為2.0×106。圖9是仿真數據經RLS-C和NLMS-C算法抑制后的目標距離元截面對比。由于自適應濾波過程的代價函數不同,RLS-C算法比NLMS-C的收斂速度快,收斂精度高。從圖9中可見,RLS-C算法有更強的雜波抑制能力,相比于NLMS-C算法,RLS-C算法抑制后目標的信噪比提升了8 dB左右。

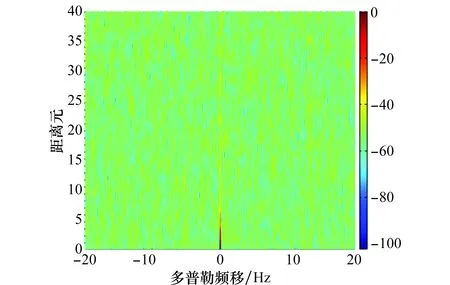
圖2 雜波抑制前的RD譜Fig.2 RD map before multipath clutter rejection

圖3 RLS算法抑制雜波后的RD譜Fig.3 RD map after multipath clutter rejection by RLS

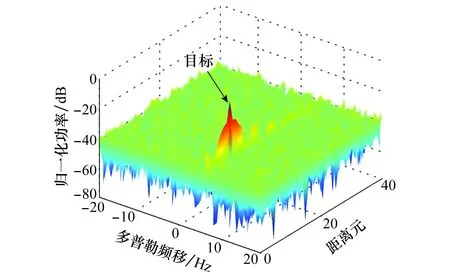
圖4 RLS-C算法抑制雜波后的RD譜Fig.4 RD map after multipath clutter rejection by RLS-C

圖5 RLS和RLS-C算法抑制后的目標距離元截面對比Fig.5 Normalized target range bin cuts after multipathclutter rejection by RLS and RLS-C

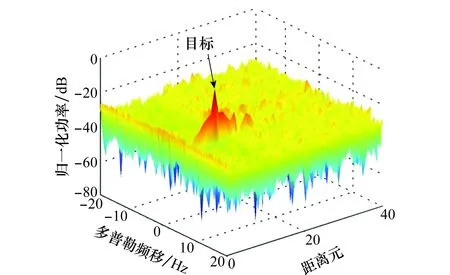
圖6 NLMS算法抑制雜波后的RD譜Fig.6 RD map after multipath clutter rejection by NLMS

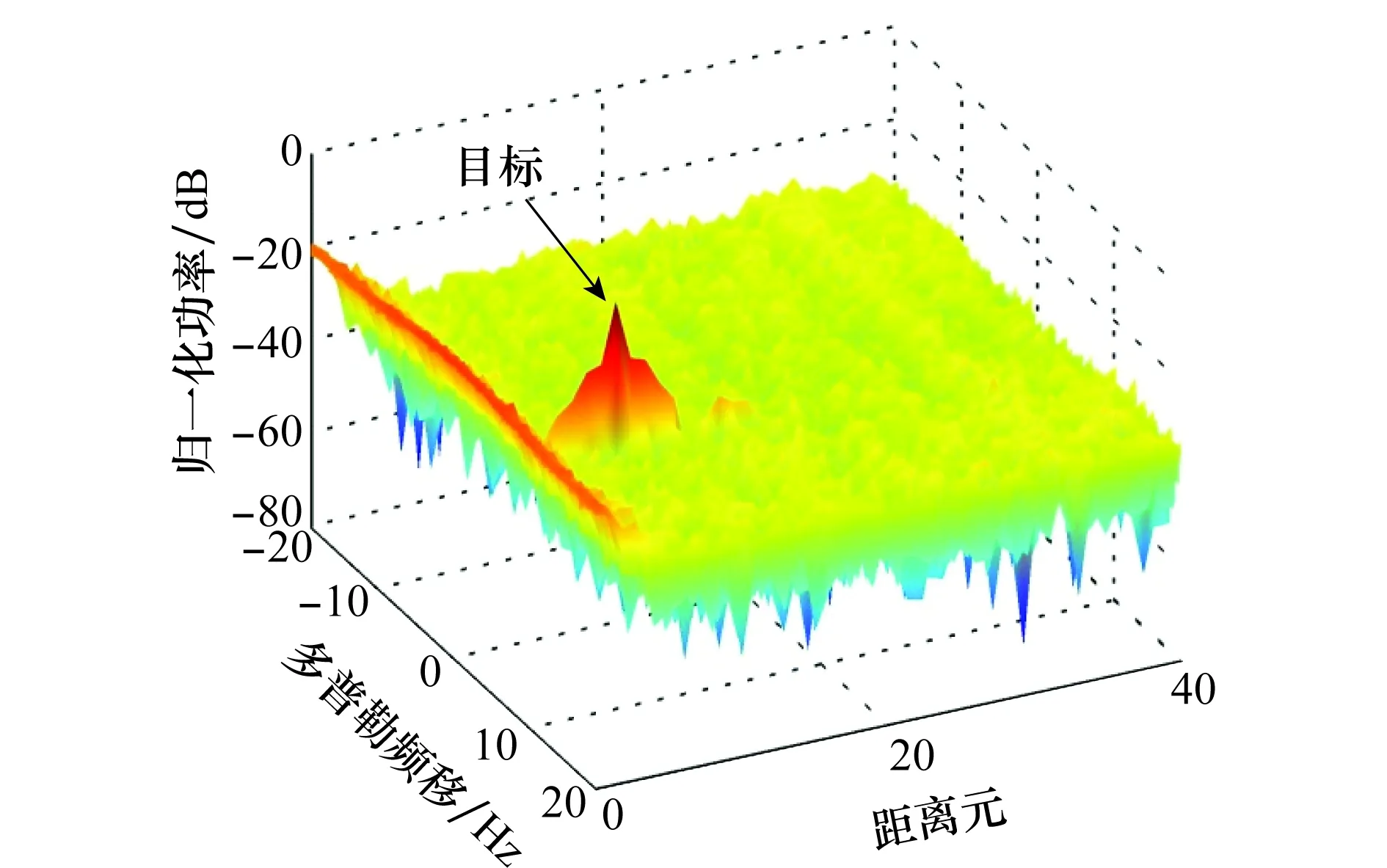
圖7 NLMS-C算法抑制雜波后的RD譜Fig.7 RD map after multipath clutter rejection by NLMS-C

3.2 實測數據結果分析

實測數據是從一個沿海的外輻射源雷達系統中獲取的,該雷達系統接收到的DRM廣播信號基本工作參數符合DRM標準B模式,發射站和接收站位于青島市和海陽市沿海,接收站位于海陽沿海,收發站之間的距離約為50 km。接收站的天線為16元線陣,參考通道和監測通道共用接收天線,通過將陣列接收天線波束形成對準發射臺和目標方向分別得到參考通道信號和監測通道信號。

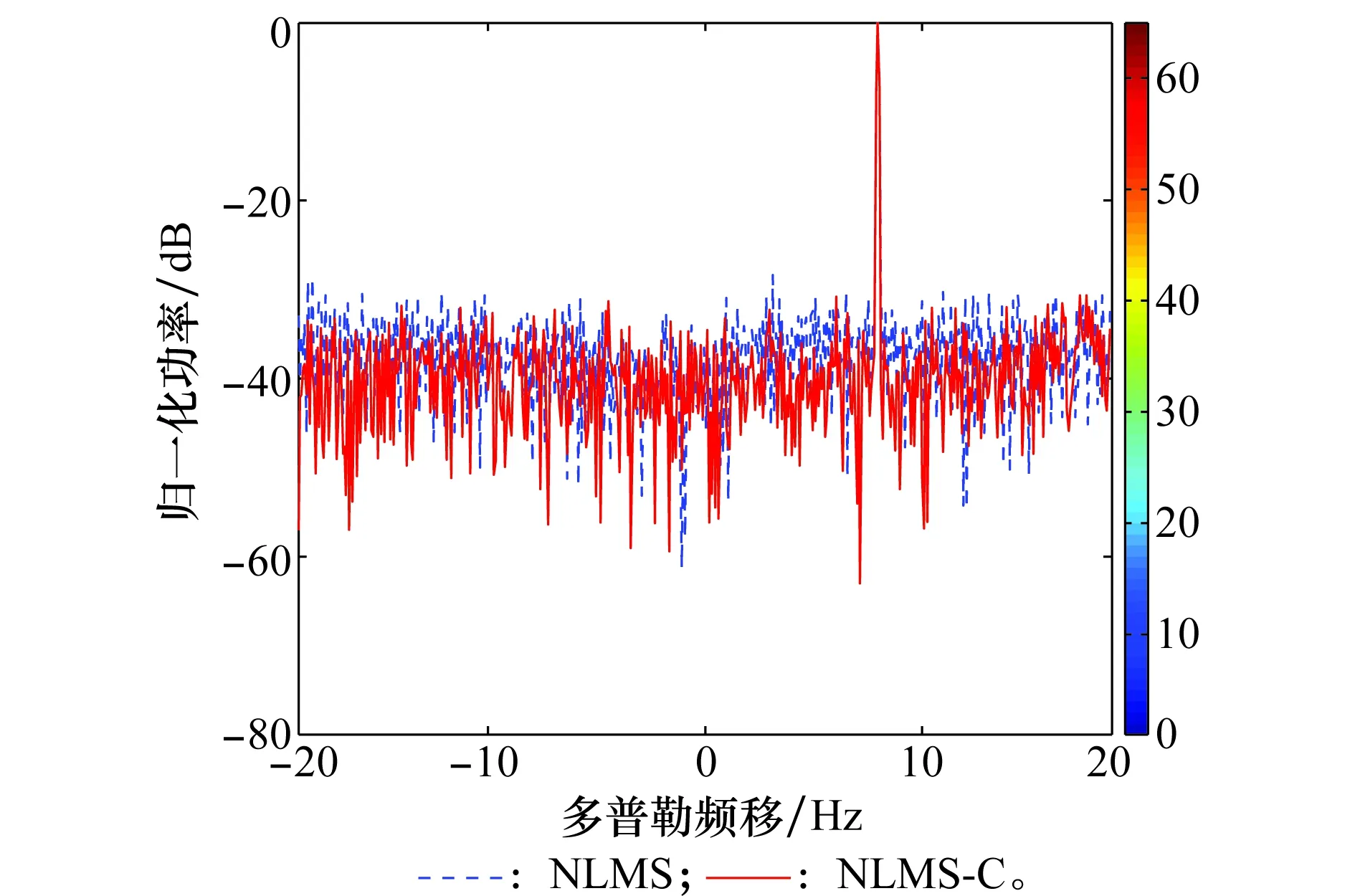
圖8 NLMS和NLMS-C算法抑制后的目標距離元截面對比Fig.8 Normalized target range bin cuts after multipath clutterrejection by NLMS and NLMS-C

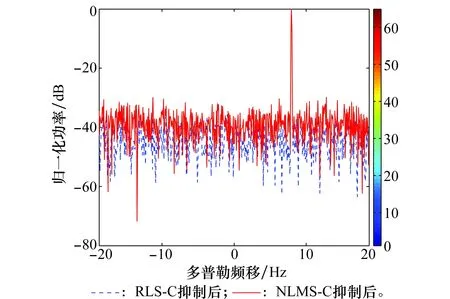
圖9 仿真數據經RLS-C和NLMS-C算法抑制后的目標距離元截面對比 Fig.9 Target range bin cuts of simulation data after rejection byRLS-C and NLMS-C

圖10是雜波抑制前監測通道信號和參考通道信號進行匹配濾波得到的RD譜,由于多徑雜波的影響,目標被完全掩蓋掉。

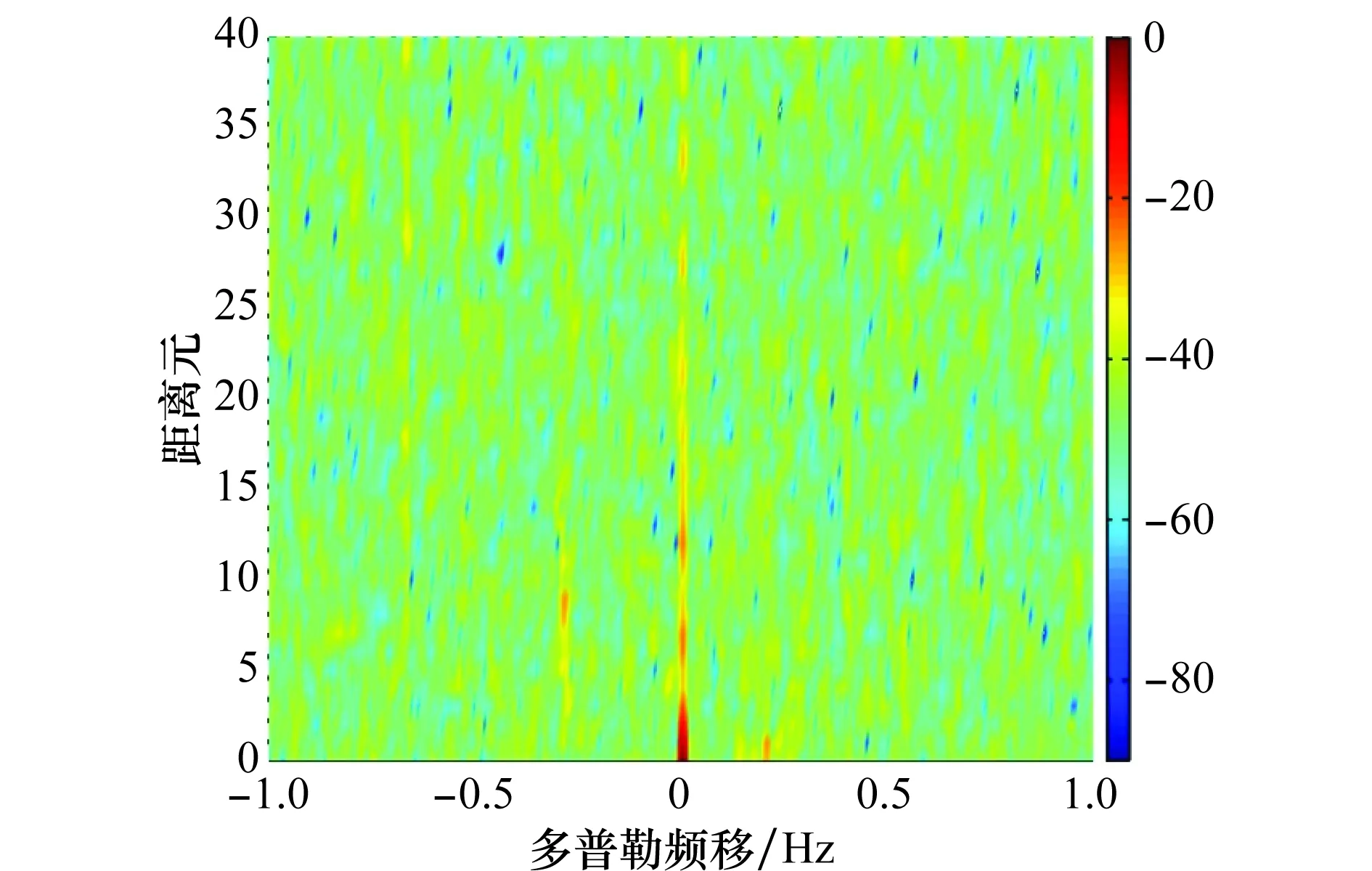
圖10 實測數據雜波抑制前的RD譜Fig.10 RD map of experiment data before multipath clutter rejection

圖11和圖12分別是經過RLS-C和NLMS-C算法抑制雜波后得到的RD譜。這兩種算法都能夠有效地抑制多徑雜波,位于距離元為5,多普勒頻移為0.033 17 Hz的艦船目標和海洋回波均凸顯出來。圖13是實測數據經RLS-C和NLMS-C算法抑制后的目標距離元截面對比。相比于NLMS-C算法,RLS-C具有更強的雜波抑制效果,目標的信噪比提升了4 dB左右。

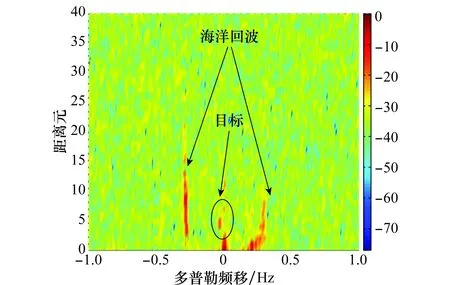
圖11 RLS-C算法雜波抑制后的實測數據RD譜Fig.11 RD map of experiment data after multipath clutterrejection by RLS-C

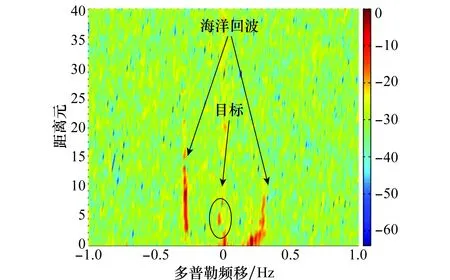
圖12 NLMS-C算法雜波抑制后的實測數據RD譜Fig.12 RD map of experiment data after multipath clutterrejection by NLMS-C

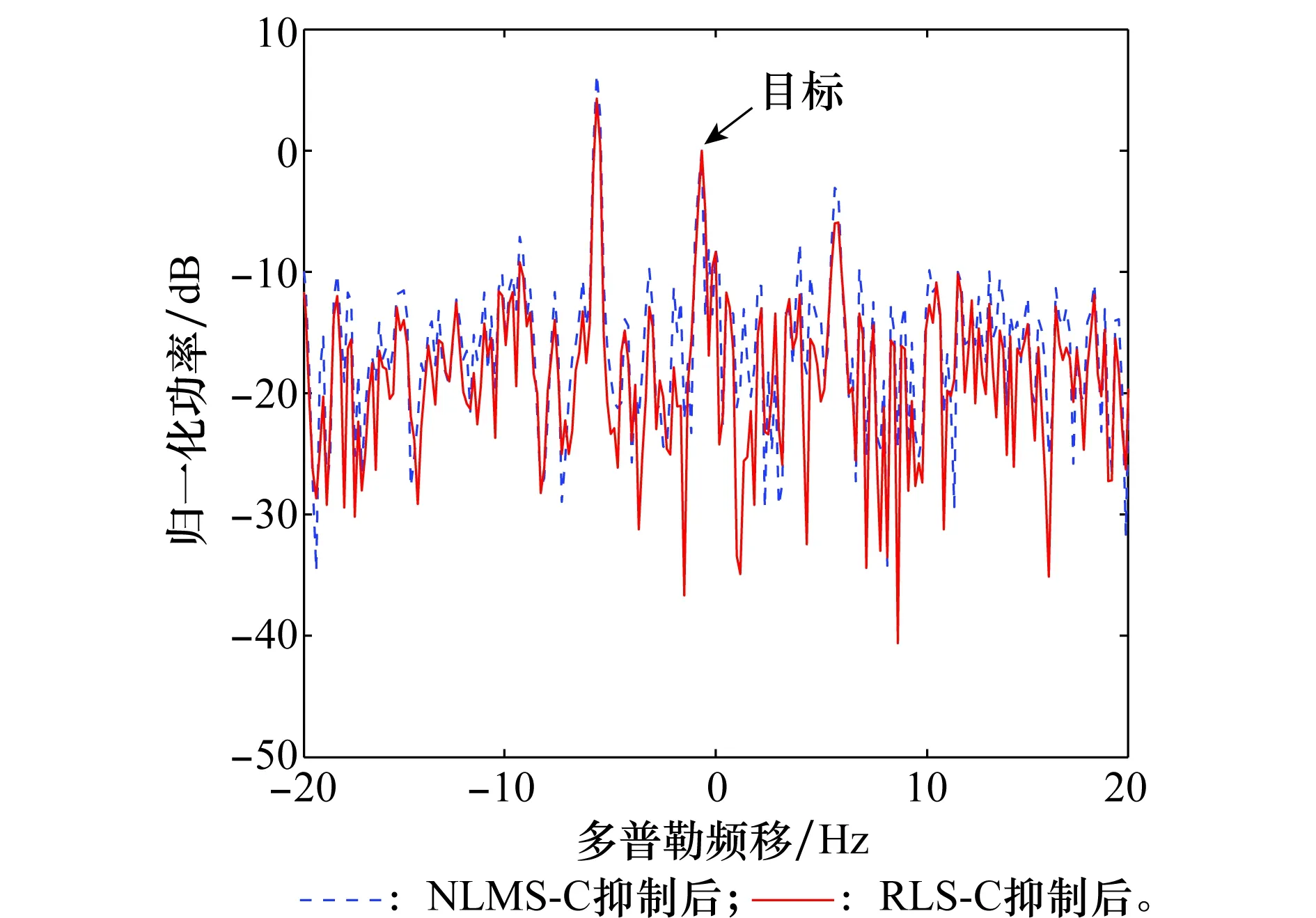
圖13 實測數據經RLS-C和NLMS-C算法抑制后的目標距離元截面對比 Fig.13 Target range bin cuts of experiment data after rejection byRLS-C and NLMS-C

4 結 論

本文以高頻DRM信號為例,研究了OFDM波形外輻射源雷達多徑雜波抑制問題,結合時域信號模型和信道特征推導了載波域信號成分組成,在此基礎上提出了分載波自適應濾波算法,并給出了所提算法的性能優勢對比分析。相比于常規時域自適應濾波算法,分載波自適應濾波算法可將濾波器的階數降為1,一方面減少了雜波抑制過程的計算復雜度,便于實時處理；另一方面,分載波自適應濾波算法的自適應濾波過程中收斂速度快,具有更強的雜波抑制能力。通過仿真和實測數據證明了分載波自適應濾波算法的有效性。對比RLS-C和NLMS-C這兩種分載波算法,RLS-C的雜波抑制效果更好。需要說明的是,本文雖以DRM廣播外輻射源雷達為例進行分析,但結果同樣適用于其他頻段的OFDM波形外輻射源雷達。