靶板在爆炸成型彈丸垂直侵徹下的層裂*

李 睿,黃正祥,祖旭東,肖強強,賈 鑫

(南京理工大學機械工程學院,江蘇 南京 210094)

層裂是靶板在彈丸沖擊載荷作用下的一種重要破壞形式，也是靶后破片形成的組成部分。研究靶板在彈丸沖擊載荷作用下的層裂效應對新型裝甲設計和靶后破片等領域具有很強的指導意義。因此，準確掌握層裂的形成機理是十分必要的。對層裂效應已展開了大量的研究。Rinehart等[1]系統分析了材料的層裂現象，提出了最大拉應力層裂破壞準則。Rinehart[2]全面介紹了應力波在靶板材料內的傳播、相互作用并產生層裂的過程。Ren等[3]提出了無網格數值模擬模型，并對鈦鋁合金在沖擊載荷下的層裂情況進行了數值模擬，發現非彈性脈沖波之間的相互作用在層裂破壞機制中起重要作用。Yu等[4]利用數值模擬和實驗相結合的方法研究了金屬材料在沖擊載荷下的多層層裂情況。杜忠華[5]研究了陶瓷靶板在沖擊載荷下層裂的形成機理，并分析了不同的彈丸速度對靶板層裂的影響。陳大年等[6]在NAG模型基礎上提出了一種基于空穴聚集的層裂模型。劉飛等[7]采用數值模擬和實驗相結合的方法研究了鋼板在接觸爆炸載荷作用下的層裂效應，認為裝藥高度、鋼板厚度和材質是影響鋼板層裂的主要因素。魏波[8]采用SPH方法，開展數值模擬研究了不同飛片速度、不同靶板厚度對鋼板和玻璃產生層裂的影響。目前對層裂效應已做了廣泛的研究，但是對爆炸成型彈丸(explosively formed projectile,EFP)侵徹靶板產生層裂效應的研究主要集中在數值模擬和實驗方面。本文中，基于波動力學和基本假設，從理論上對在EFP沖擊載荷作用下靶板發生層裂的過程進行分析，在不考慮EFP強度的基礎上建立相應的力學模型，研究靶板厚度和EFP速度對靶板層裂的影響，并通過實驗驗證理論模型的可靠性。

1 理論模型

1.1 應力波的形成和傳播

在EFP垂直侵徹靶板的過程中，由于應力波的相互作用，在靶板背面產生層裂。由于EFP侵徹入孔情況與靶后效應無關，因此本文中暫不考慮，主要研究靶板背面層裂區域的形狀和范圍。為了便于公式推導和簡化計算，作如下幾點假設：(1)在侵徹靶板過程中將EFP當作圓柱桿；(2)應力波在靶板內以球面波的形式傳播；(3)不考慮應力波的衰減；(4)靶板材料均勻無缺陷。根據適用于高速撞擊的A-T模型，EFP侵徹靶板時的侵徹速度為：

(1)

式中：vj為EFP著靶速度，ρj為構成EFP材料的密度，ρt為靶板材料密度，Rt為靶板材料侵徹阻抗。

EFP在侵徹靶板時，在靶板慣性作用下，孔徑開始增長，同時產生的應力波在靶板中以球面波的形式傳播。孔徑增長開始時孔壁的初始壓力等于軸向壓力，因此可以得到：

(2)

式中：p0為初始孔徑增長壓力。

徑向壓力pc與初始孔徑增長壓力的關系為:

(3)

式中：r0為EFP的初始半徑，rc為侵徹孔半徑。

由文獻[9]可知，在EFP侵徹靶板過程中，隨著孔徑的增長，應力波以球形波在靶板中傳播，不同半徑r處的應力波強度為:

(4)

式中：Y為靶板的屈服強度，uc為孔徑增長速度。

由文獻[10]可知，不同孔徑處的孔徑增長速度為:

(5)

對式(5)對時間求導，則可得到:

(6)

由Szendrei-Held方程[11]可知侵徹孔徑rc隨時間t的變化為:

(7)

圖1 入射波和反射波相互作用示意圖Fig.1 Schematic diagram of interaction between incident and reflected waves

1.2 應力波的反射和層裂的形成

當應力波傳播到靶板背面時發生斜反射，則反射波為:

σf=Rσt(r)

(8)

式中：R為反射系數[2]，且：

(9)

式中：α為入射角，β為反射橫波的反射角。

EFP侵徹靶板過程中形成的應力波在靶板自由端反射后形成反射拉伸波，在反射波的傳播過程中，入射波和反射波在靶內相互作用形成合應力波。應力波和反射拉伸波相互作用的幾何關系如圖1所示，t0時刻EFP侵徹到A0點，假設此時產生的應力波以入射角α傳播到B點，在B點形成反射波并向前傳播到某一點C，與t時間后侵徹界面A點產生的應力波在C點相互作用，形成拉伸應力波。按臨界應力斷裂準則，若拉伸應力波強度達到臨界斷裂應力σct時，即:

σt≥σct

(10)

則靶板背面出現層裂，在靶板內形成裂紋。

由文獻[2]可知，兩應力波斜交下的合應力強度為:

(11)

式中：σa為由A點產生的與反射拉伸波σf相互作用的應力波強度，ν為靶板材料泊松比。

由臨界斷裂準則可知，當該合應力波強度σt達到臨界斷裂應力σct時，發生層裂。由式(4)、式(10)和式(11)組成方程組，可確定該層裂點距初始入射波陣面的距離r。

1.3 層裂點位置計算

根據圖1，在t0時刻EFP侵徹到A點，在入射波從A0點傳播到B點再反射傳播到某一點C的這段時間里，侵徹界面由A0點侵徹到A點，前進的距離為:

r2=uΔt

(12)

侵徹界面產生的應力波在自由端反射，A0點距反射點B的距離為:

r0=(h-ut)/cosα

(13)

A點距反射點B的距離為:

(14)

由幾何關系可知:

(15)

侵徹界面到達A點的時間為:

t=t0+(r0+s)/vt

(16)

式中：vt為RHA材料中縱波的體積波速。

由式(12)～(16)可知，層裂點C距t時刻侵徹界面A點的相對位置為:

(17)

以靶板背面所在平面為橫軸、靶板厚度方向為縱軸建立坐標系，坐標原點為侵徹孔徑軸線與靶板背面的交點，則層裂點C的坐標可以表示為:

x=rsinθ,y=h-ut-rcosθ

(18)

1.4 理論結果分析

圖2 不同EFP速度下靶板背面發生層裂的區域Fig.2 Spallation zones at target backs at different EFP velocities

基于建立的理論模型和Matlab軟件，對EFP侵徹有限厚靶板的過程進行計算，EFP材料為高導無氧銅，密度ρj=8.96 g/cm3；軋制均質裝甲[12](rolled homogeneous armor，RHA)密度ρt=7.86 g/cm3，屈服強度Y=1.5 GPa，泊松比為ν=0.28。計算過程中EFP半徑為21.5 mm，垂直侵徹RHA靶板。

轉染48 h后，流式細胞術檢測各組SHG-44細胞凋亡情況，結果顯示miR-543 mimic組與mimic NC組相比細胞凋亡率顯著增加(P＜0.01);miR-543 inhibitor組與inhibitor NC組相比，細胞凋亡率顯著減少(P＜0.01)，見表2和圖4。由此可見，過表達miR-543可促進SHG-44細胞凋亡，抑制miR-543表達可抑制細胞凋亡。

1.4.1不同速度對靶板層裂的影響

根據理論分析，EFP侵徹靶板過程中產生的應力波的強度與EFP著靶速度密切相關，而靶板能否發生層裂取決于應力波和反射應力波相互作用后的拉應力波強度的大小，因此EFP的著靶速度是影響層裂的主要因素之一。在靶板厚度h=40 mm的情況下，EFP分別以1 550、1 600、1 700、1 750、1 800、1 850、1 900、1 950和2 000 m/s的著靶速度侵徹靶板，靶板背面發生層裂的區域見圖2。

應力波以球面波的形式傳入靶板，隨著入射角的增大，到達自由表面的路程不斷增加，反射拉應力波的強度隨入射角的增大而減小。因此層裂的厚度隨入射角的增大而增大。綜合效果，使靶板背面出現彎月形的層裂區域，如圖2所示。在計算條件下，當EFP的著靶速度不同時，彎月形層裂區域的形狀不同。隨著EFP著靶速度的增大，彎月形層裂區域的厚度不斷減小，層裂區域的長度不斷增大。EFP速度從1 550 m/s增大到1 900 m/s時，靶板背面層裂區厚度從21.8 mm減小到3.9 mm，彎月形層裂區長度從86.4 mm增大到133.4 mm。這是因為增大EFP著靶速度，而入射波到自由表面的衰減量不變，因此反射波強度增大，于是層裂時刻提前，靶板背面的層裂厚度減小。當速度大于1 900 m/s時，層裂區域的面積急劇衰減，并且層裂區域形狀也不再是彎月形。當速度達到2 000 m/s時，層裂長度為12 mm，厚度為2 mm，此時對靶后效應影響甚微。

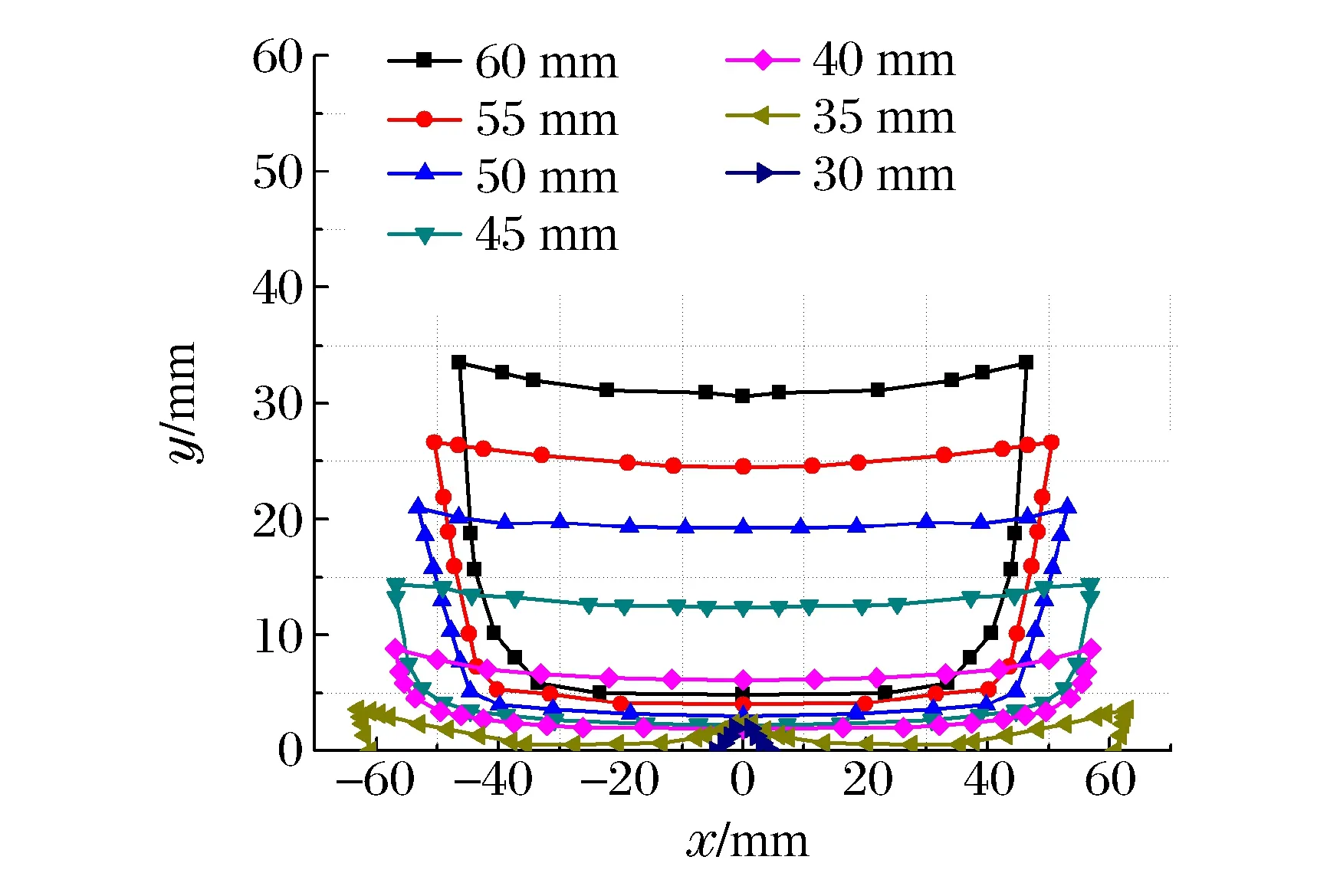
圖3 不同厚度靶板背面發生層裂的區域Fig.3 Spallation zones at target backs with different thicknesses

1.4.2不同厚度對靶板層裂的影響

根據理論分析，在給定EFP參數的基礎上，靶板厚度直接影響反射應力波的強度，因此靶板厚度是靶板發生層裂的重要影響因素。在EFP著靶速度為1 800 m/s情況下，分別侵徹30、35、40、45、50、55和60 mm厚的靶板，靶板背面發生層裂的區域如圖3所示。

2 實驗驗證

2.1 實驗布置

采用?140 mm的無殼體成型裝藥。針對EFP在7倍炸高下穿透40 mm厚RHA靶板進行實驗。聚能裝藥如圖4所示，裝藥直徑為140 mm，裝藥長度為102 mm，炸藥為JH-2。藥型罩材料為紫銅，變壁厚，采用8#電雷管起爆。EFP藥型罩如圖5所示，經數值計算，EFP半徑為21.5 mm，長度為83.5 mm，速度為1 800 m/s。為了完整地回收靶后崩落的碎片，采用注滿水的水箱來回收靶后破片；成型裝藥以垂直方式布設，以保證EFP垂直入射RHA靶板；靶板距水面1 000 mm，實驗現場布置見圖6。在上述實驗情況下，共進行2發驗證實驗。

圖4 成型裝藥Fig.4 Photograph of shaped charge

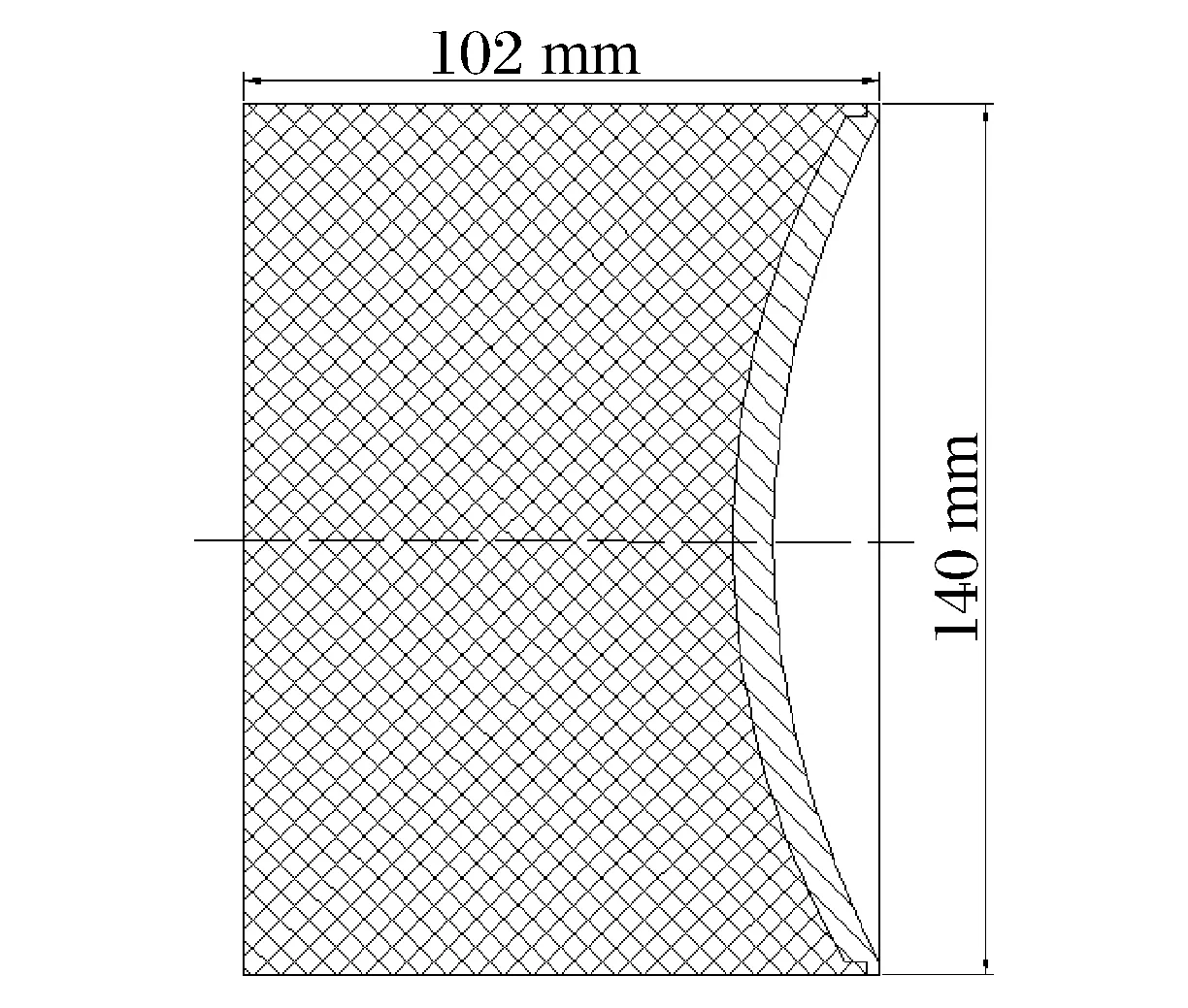
圖5 EFP藥型罩Fig.5 Diagram of EFP liner

圖6 侵徹實驗現場布置Fig.6 Layout of penetration experiment

2.2 實驗結果分析

由于EFP侵徹靶板過程中在靶板背面形成彎月形的層裂區域，因此層裂的厚度不均勻，理論結果和實驗結果如圖7所示。分別測量圖7中實驗所得的層裂參數，層裂厚度取層裂區域最外側處裂紋消失處的厚度，理論計算和實驗結果見表1。

利用?140 mm成型裝藥形成EFP對40 mm厚裝甲鋼靶板進行侵徹，實驗后靶板發生層裂。由表中結果可知，理論計算結果與實驗結果吻合較好，層裂的厚度和長度與實驗1的誤差分別為4.76%和2.89%；與實驗2的誤差分別為3.30%和1.81%。驗證了EFP侵徹有限厚靶板形成層裂理論分析模型是正確的。

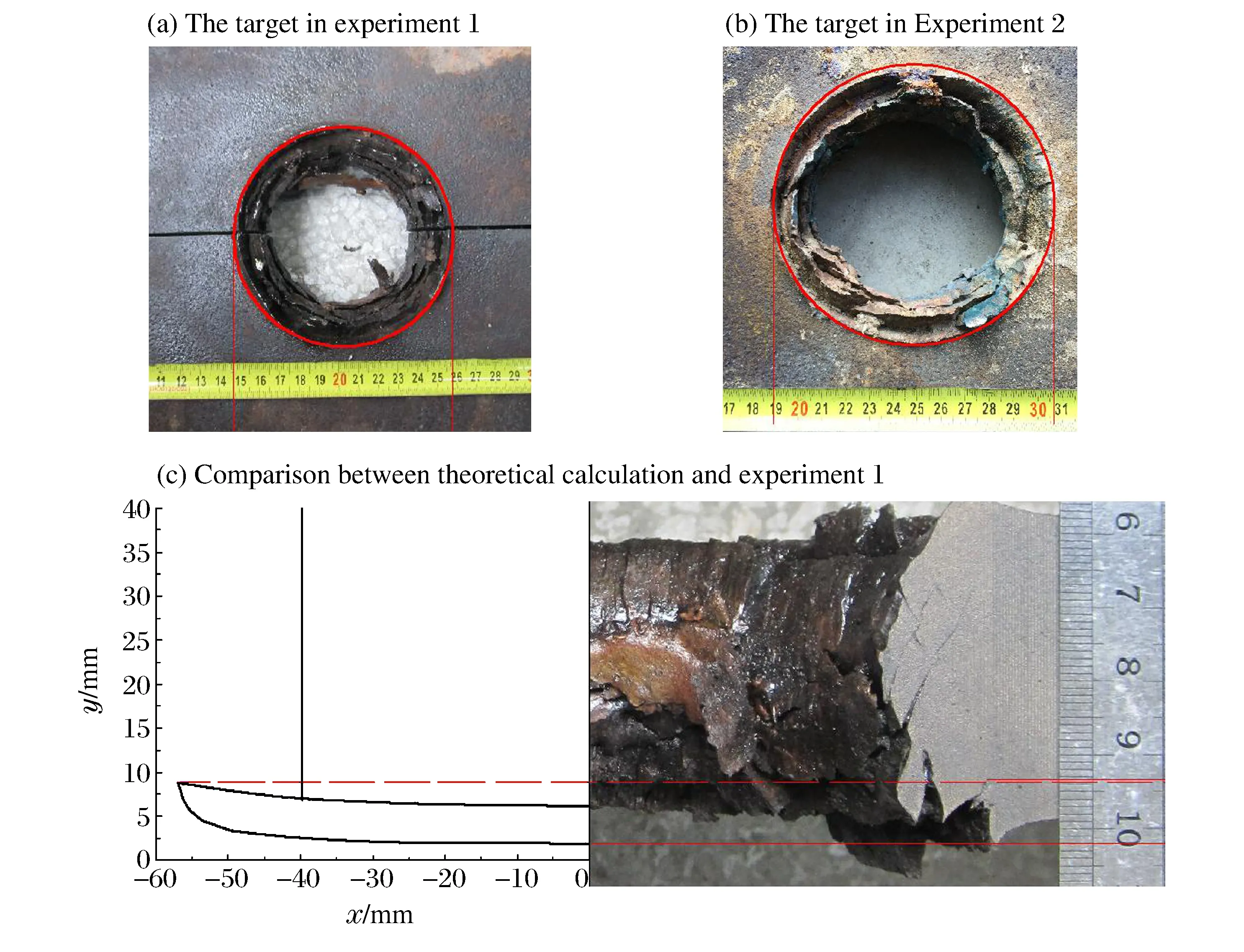
圖7 實驗與理論計算結果Fig.7 Experimental and theoretical results

層裂厚度/mm理論計算實驗1實驗 2層裂長度/mm理論計算實驗1實驗 28.88.49.1114.0110.8116.1

3 結 論

(1)利用應力波傳播特性，理論分析了EFP侵徹有限厚靶板形成層裂的過程，得到了計算層裂點位置的表達式。

(2)編程計算了在靶板厚度h=40 mm不變的情況下，不同的EFP著靶速度vj對層裂的影響，計算結果表明，速度在1 500～1 900 m/s范圍內，隨著EFP著靶速度的增大，彎月形層裂區厚度不斷減小，長度不斷增大。EFP著靶速度大于1 900 m/s時，層裂區域形狀不再呈彎月形，層裂區域急劇縮小。

(3)利用Matlab軟件編程計算了在vj=1 800 m/s不變的情況下，不同靶板厚度對層裂的影響，計算結果表明，靶板厚度在35～60 mm范圍內，隨著靶板厚度的增大，彎月形層裂區厚度不斷增大，長度不斷減小。當靶板厚度小于35 mm時，層裂區域形狀不再呈彎月形，層裂區域急劇縮小。

(4)根據EFP侵徹實驗，得到在vj=1 800 m/s且h=40 mm情況下，靶板發生層裂時的參數。同時利用EFP垂直侵徹有限厚裝甲鋼靶板形成層裂理論對在相同條件下靶板層裂情況進行計算，兩者結果吻合較好。