靶板厚度對卵形彈丸垂直貫穿中等厚度 混凝土靶的影響*

劉志林,王曉鳴,李文彬,姚文進,宋梅利

(南京理工大學智能彈藥技術國防重點學科實驗室,江蘇 南京 210094)

與深侵徹研究類似，彈丸貫穿有限厚度靶的研究對先進鉆地武器的研究和防護設計工程具有重要的意義。彈丸貫穿靶體是一個復雜的過程，當彈丸貫穿混凝土靶后，靶板破壞嚴重，靶板背面產生大面積崩落的混凝土碎塊，從而對掩體內的人員和設備造成嚴重的次生破壞。現有的ACE、NDRC等經驗公式[1]都可以對彈丸侵徹和貫穿混凝土介質的侵徹深度和彈道極限進行較為有效的工程預測，但由于使用范圍的限制，很難得到更為廣泛的應用。近年來很多方法，包括解析模型和數值分析模型，都可以對各種彈體貫穿薄靶進行預測，Hanchak等[2]、Yankelevsky[3]、Dancygier[4]、葛濤等[5]都對彈丸貫穿混凝土問題做了研究。相對于半無限靶的深侵徹研究，有限靶的貫穿問題主要涉及到靶背效應問題，由于混凝土的拉伸強度遠遠小于其壓縮強度，彈丸侵徹過程中會形成壓縮波并向彈丸前進方向傳播，當壓縮波傳播到靶體背面的自由面時，壓縮波反射之后變為拉伸波。當應力超過混凝土的抗拉強度時，混凝土會發生斷裂，并形成靶背的崩落現象。混凝土介質材料的動態力學性能主要由其狀態方程、強度方程和失效準則三個方程表征。侵徹問題中的混凝土本構最常用的是HJC 模型[6]，HJC 模型主要綜合考慮了大應變、高應變率、高壓效應等因素，較為適合Lagrangian和Euler網格下的計算模擬，其等效屈服強度與靜水壓力、應變率以及損傷的函數，結合三階段的狀態方程，其模擬彈丸深侵徹問題十分適用，模擬結果精確。但此模型沒有考慮第三不變應力張量的影響，且其不能很好地模擬開坑、剝落等現象。

為了研究卵形彈丸的貫穿中等厚度混凝土靶體的靶體厚度對剩余速度的影響規律，本文中利用火炮發射平臺，采用次口徑發射技術，開展了60 mm直徑彈丸貫穿不同厚度混凝土靶的實驗研究。結合無網格方法、考慮3個極限面的RHT混凝土本構和多孔介質p-α狀態方程，對彈丸貫穿薄靶和厚靶的貫穿效應進行了模擬，分析了彈丸貫穿過程以及其損傷演化，獲得了不同厚度靶對貫穿的影響規律。

1 實 驗

1.1 實驗方案

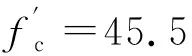
圖1 實驗場地布置圖Fig.1 Layout of experimental site

圖2 彈體裝配實物Fig.2 Photograph of assembled projectile

1.2 實驗結果

彈丸貫穿混凝土的實驗中，撞擊速度和貫穿余速是實驗中需要測量的重要參數。實驗中采用高速攝像機用于彈丸入靶姿態捕捉和入靶前撞擊速度的測量，以及彈丸穿透靶板后彈丸出靶姿態和出靶速度的測量。

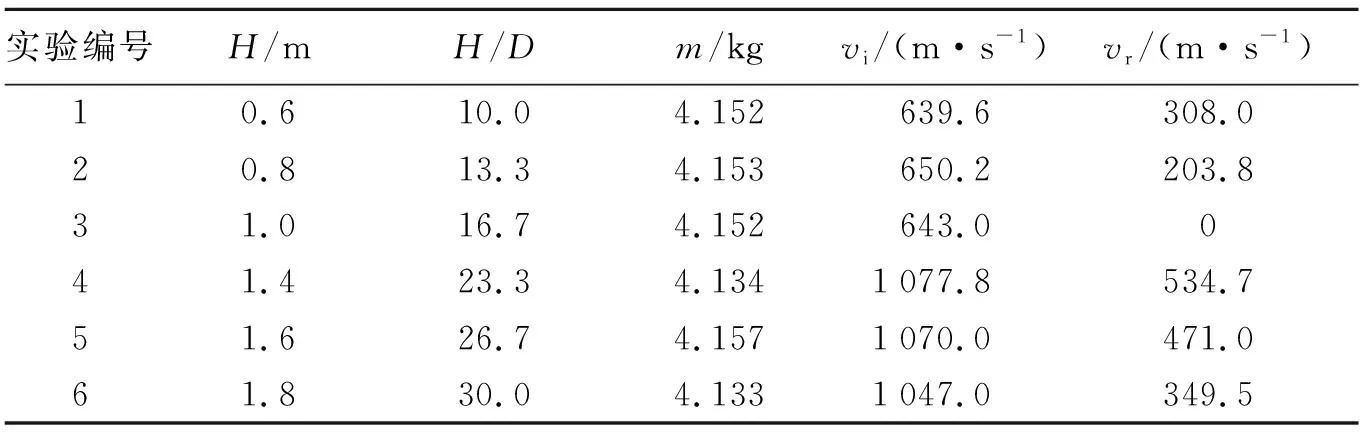
表1 實驗結果Table 1 Experimental results

實驗結果如表1所示，結果顯示彈丸的撞擊速度與設計速度相當，除3號射擊外其余5發射擊實驗的彈丸都貫穿了混凝土靶體，被貫穿后靶體的破壞狀態如圖3～4所示。

圖3 1號工況下靶體破壞圖Fig.3 Failure of concrete target after impact under case 1

圖4 3號工況下靶體破壞圖Fig.4 Failure of concrete target after impact under case 3

從圖3～4中可以看出靶體呈整體破壞，且多處徑向擴展的宏觀裂紋發展到靶體側面，迎彈面有漏斗形開坑區。靶背有大面的崩落區，崩落區的面積與深度明顯大于迎彈面的開坑面積和深度。其他4 種貫穿射擊后的靶體破壞與1號射擊工況類似。3號射擊工況與其他5發射擊結果不同，實驗后的彈丸停留在靶體背面，靶體的背面有很大崩落區，彈丸的頭部裸露在靶體外，如圖4(b)所示。靶體的迎彈面和其他靶體的現象類似，有類似于圓形的開坑區。3號射擊工況結果顯示，此發射擊條件下靶板的厚度非常接近此侵徹速度下的靶板的震塌破壞臨界厚度。

2 數值模型

2.1 侵徹模型

圖5為本文數值模擬采用的侵徹模型，模型尺寸與實驗尺寸比為1∶1，彈丸采用Lagrangian網格，見圖6；靶板采用SPH粒子單元，粒子間距為2.5 mm，計算模型采用軸對稱模型。

圖5 侵徹模型Fig.5 Penetration model

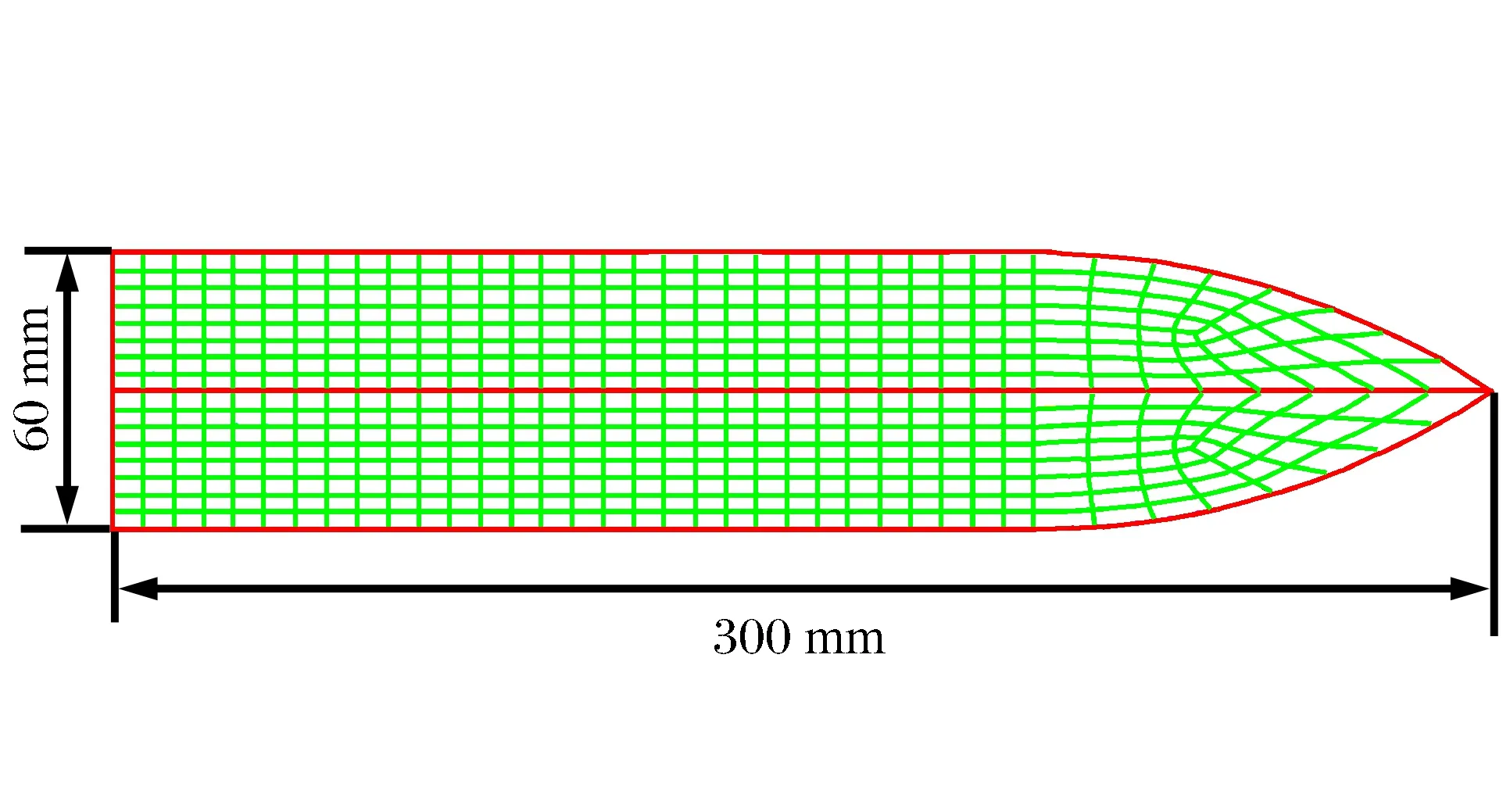
圖6 彈體網格劃分Fig.6 Mesh division of projectile calculation model

2.2 混凝土本構及參數

選用RHT模型[7]作為貫穿模擬的混凝土介質本構，RHT模型最早是由Riedel等提出的混凝土本構模型，其是由3個極限面(彈性極限面、失效面、剩余強度面)來描述混凝土的動態力學性能。該模型考慮了第三不變應力偏張量的影響，在預測混凝土深侵徹方面結果理想，且在描述侵徹過程中的混凝土損傷變化有一定的優勢。本文中結合SPH方法和RHT混凝土本構以及多孔介質p-α狀態方程，模擬彈丸侵徹貫穿混凝土過程，研究彈丸開坑和崩落現象發生過程，同樣為研究貫穿工程模型提供數據支持，混凝土材料的具體參數可參考文獻[8-10]。

3 結果與討論

3.1 貫穿過程分析

數值模擬以復現貫穿實驗為目的，主要是研究彈丸在同一速度下撞擊不同厚度靶體后的彈丸余速的規律。計算中的靶板厚度在10～30D范圍內，速度有650 m/s低速和1 100 m/s高速。此工況下，彈丸的貫穿過程分為3個階段穿透，分別為開坑段、隧道段和出靶段。

圖7顯示了彈丸以650 m/s速度撞擊0.8 m厚混凝土靶板的數值計算結果的損傷演化過程圖，損傷云圖中紅色代表材料完全損傷，藍色代表未損傷，在RHT模型中的損傷δ是材料的塑性應變增量的積累與材料失效塑性應變的比值，其值在0到1范圍內。取t=2.6 ms時刻的靶板損傷為最終損傷狀態，在t=2.6 ms時刻，靶板的開坑區、隧道區和沖切區都非常明顯。2號射擊工況的彈丸余速比1號射擊工況的低，彈丸與沖切區混凝土的相互作用持續的時間較長，沖切區的混凝土沖出的速度較1號射擊工況的小，1號射擊工況測得的彈丸余速為308 m/s，數值計算彈丸余速結果為379 m/s，彈丸在沖切段與混凝土的響應主要以局部響應為主，彈丸貫穿了損傷后的沖切區的混凝土，彈丸頭部會穿透整個靶面，且繼續向外飛行，與混凝土完全分離。沖切區混凝土在與彈丸分離后向外飛散，且離隧道區近的碎片速度較大，這一結果與實驗結果完全一致。在靶背影響區域內的彈丸消耗的能量情況見表2，結果顯示了彈丸余速越小，彈丸在靶背影響區域消耗的動能越大，表明彈丸余速越小，與混凝土作用時間越長，損失的能量越大。

圖7 靶被貫穿過程損傷云圖Fig.7 Damage contour of target during penetration process

實驗編號H/D進入靶背影響區的速度/(m·s-1)彈丸消耗的能量/J110.04601.4×105213.34342.8×105316.74283.8×105423.36302.0×105526.75412.2×105630.05023.2×105

圖8 靶被貫穿破壞的數值模擬結果 Fig.8 Simulation results of concrete target damage

在6發射擊的貫穿過程中，除3號射擊工況外，其余5發貫穿的余速都相對比較高(大于200 m/s)，其貫穿過程與1號射擊情況工況類似。將3號發射工況的靶背最終破壞情況的數值模擬結果(圖8)與實驗結果(圖9)進行對比發現，數值模擬結果與實驗一致，此工況下的彈丸停留在靶體內部，且靶后有大質量塊混凝土被沖切出靶體。彈丸的侵徹深度為74.2 cm(實驗值為79.5 cm)，沖切出的靶體的飛濺速度在6 m/s。3號射擊工況的彈丸的余速為零，實驗中3號射擊工況高速錄像靶后破壞過程見圖9(b)，靶后有大體積混凝土塊向外沖出，且混凝土塊整體以一速度向外飛出(混凝土塊的飛出速度約為17 m/s)，可以判斷，混凝土塊發生沖切破壞。圖9(a)顯示了3號射擊工況的靶板背面的破壞形態，中間發光物體的為停留在靶體中的彈丸，彈丸頭部裸露在空氣中，彈身埋沒在靶體中。結果表明在彈丸沖擊厚靶時，當彈丸在靶背影響區時彈丸速度很小時，沖出靶體的混凝土塊與彈丸的響應以整體響應為主。

圖9 靶被貫穿破壞的實驗結果Fig.9 Experimental results of concrete target damage

3.2 過載分析

圖10～11所示分別為在實驗條件下的彈丸的速度和過載變化歷程數值模擬結果，6條曲線分別代表了實驗的6發射擊工況。數值模擬中彈丸的撞擊速度分為2種，為650和1 100 m/s，靶板厚度有6種，分別為0.6、0.8、1.0、1.4、1.6 和1.8 m。速度變化曲線顯示，同一撞擊速度下，隨著靶板厚度的增加，彈丸的余速呈下降趨勢；靶板厚度繼續增加時，余速逐漸趨向于零，即彈丸沒有貫穿靶板。相同撞擊速度撞擊不同厚度靶板的速度變化曲線圖中，彈丸在撞擊靶板后的速度曲線基本重合，在彈丸接近靶板靶背的自由面時，速度變化趨于平緩，直至彈丸貫穿整個靶板，速度趨于恒定值，也就是彈丸的貫穿余速，結果表明計算值與實驗值吻合較好。

圖10 彈丸速度時程曲線 Fig.10 Velocity-time curve of projectile

圖11 彈丸過載時程曲線Fig.11 Acceleration-time curve of projectile

圖12所示為彈丸撞擊不同厚度靶的過載隨時間的變化，彈丸撞擊靶板后彈丸過載陡然上升直至穩定侵徹階段，穩定侵徹階段彈丸過載趨于恒定值，650 m/s速度下彈丸穩定侵徹的過載接近30 000g，1 100 m/s速度下約為35 000g。Rosenberg等[11]和Chen等[12]在對混凝土的常阻力假設的適用的初始撞擊速度閾值達到1 200 m/s，本文的數值計算結果也就印證了這一結果。在彈丸繼續侵徹，并接近靶背自由面時，彈丸的過載開始降低，并緩慢將至零，表明彈丸停止運動，或是彈丸完全貫穿混凝土靶。圖12(a)為彈丸貫穿0.6 m 厚靶的彈丸過載隨彈丸位移的曲線圖，過載可以分為3個階段：開坑階段、隧道階段(穩定侵徹階段)和靶背自由面影響階段。侵徹實驗中，彈丸的開坑深度的散布較大，Forrestal等[13]建議開坑區的深度為2D，數值模擬結果顯示，彈丸從開坑階段進入穩定侵徹階段的過渡區域也在深度2D處附近，本文取2D作為開坑階段與穩定侵徹階段的分界線；穩定侵徹階段的彈丸過載接近為恒定值，穩定侵徹階段結束的分界線由靶背自由面的影響區域決定，數值模擬中0.6 m的靶板的貫穿的自由面影響區域約在3.1D。自由面影響區域內，彈丸的過載逐漸降低直至為零。特別的，當彈丸頭部運動至靶體背面的自由面時(Z=10D)，彈丸的過載還并未降至零，表明被彈丸沖出混凝土靶體的混凝土介質對彈丸還會有作用力。這3個分界時刻的損傷云圖見圖13，從損傷云圖中可以發現，彈丸在開坑段以及穩定侵徹的過程中，離靶背3.1D厚度的區域內損傷積累相對于其他區域較為嚴重，當彈丸行至此區域時，彈丸過載穩步降低直至為零。

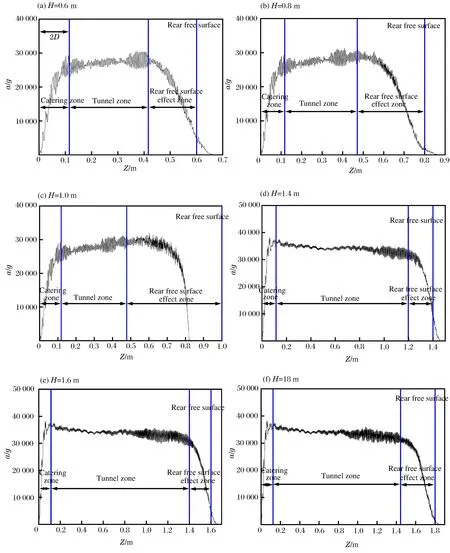
圖12 彈丸過載與位移關系Fig.12 Relation between acceleration and displacement

厚度為0.8 m靶被貫穿的3個階段與厚度為0.6 m靶被貫穿的過程類似，但靶背影響區域較厚度為0.6 m的靶有一定的增加(約5.6D)，彈丸貫穿厚度為1.4、1.6、和1.8 m靶的過載隨位移的變化圖見圖12(d)～(f)，高速貫穿的過載曲線與低速相比，彈丸的開坑區域的厚度相對減小，表明彈丸更快的進入穩定侵徹階段，但其減小的幅值有限，因開坑段不是本文研究的重點，本文中還是取2D作為開坑區的深度。隨著靶板厚度的增加，隧道區域的厚度逐漸增加，靶背影響區的厚度也逐漸增加，彈丸的余速逐漸減小，隧道區的長度與靶背影響區的長度的數值模擬結果見表3。

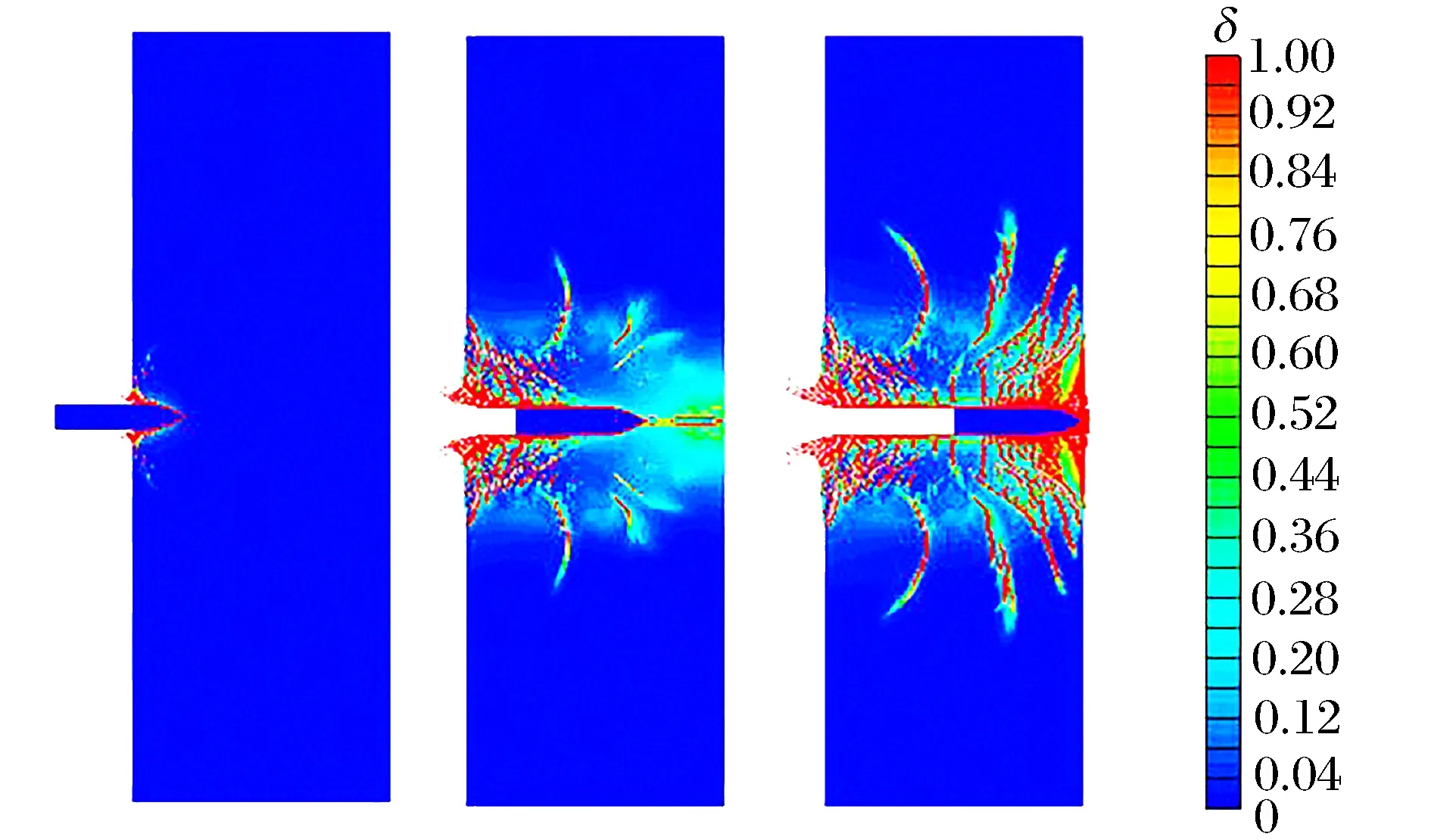
圖13 3個分界時刻的損傷云圖Fig.13 Damage contour of different stages in penetration process at three instants of time

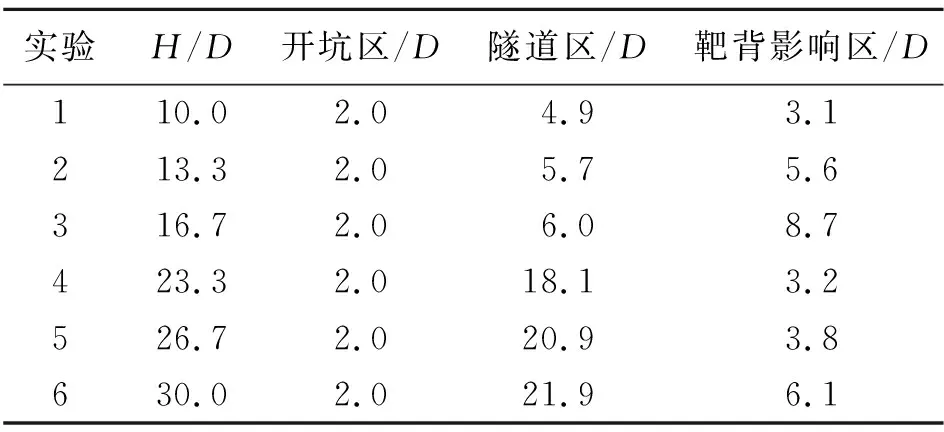
實驗H/D開坑區/D隧道區/D靶背影響區/D110.02.04.93.1213.32.05.75.6316.72.06.08.7423.32.018.13.2526.72.020.93.8630.02.021.96.1

4 結 論

開展 60mm直徑彈丸的貫穿中等厚度混凝土介質靶實驗，靶體厚度在10～30D范圍內，撞擊速度為650和1 100 m/s，得到彈丸以相同速度撞擊不同厚度混凝土介質靶體的彈丸余速變化規律。結合SPH無網格方法以及RHT混凝土本構以及考慮多孔特性的p-α狀態方程，對實驗工況進行的數值模擬，對實驗結果和數值模擬結果進行分析總結，得出以下結論：

(1)采用的SPH無網格法結合RHT混凝土本構和考慮多孔特性的p-α狀態方程方法，可以很好地模擬靶板的開坑與崩落失效響應，在彈丸貫穿混凝土介質問題的研究中取得較好的結果。

(2)貫穿實驗表明：彈丸的剩余速度隨著混凝土靶體厚度的增加而降低；隧道區和靶背影響區的厚度隨著靶體整體厚度的增加而增加。

(3)數值模擬結果表明：在彈丸出靶速度低于閾值時，混凝土靶背發生沖塞現象；彈丸余速較大時，彈丸出靶時與沖切區的混凝土繼續作用，彈丸在此過程中的過載穩步下降直至彈丸頭部穿透靶板，過載降為零。