二次電子倍增對(duì)射頻平板腔建場(chǎng)過程的影響?

董燁1)劉慶想 龐健 周海京 董志偉

1)(西南交通大學(xué)物理科學(xué)與技術(shù)學(xué)院,成都 610031)2)(北京應(yīng)用物理與計(jì)算數(shù)學(xué)研究所,北京 100094)3)(中國(guó)工程物理研究院流體物理研究所,綿陽 621900)(2018年4月11日收到;2018年6月14日收到修改稿)

1 引 言

二次電子倍增是由二次電子發(fā)射引起的一種真空共振放電現(xiàn)象,其可以在很多結(jié)構(gòu)下產(chǎn)生,如:加速器、微波器件的腔體結(jié)構(gòu)表面、微波輸出窗表面以及人造衛(wèi)星敏感器件內(nèi)部,并導(dǎo)致嚴(yán)重后果,包括射頻擊穿、建場(chǎng)失敗、沿面閃絡(luò)以及噪聲干擾等.作為一種最為基本的二次電子倍增類型,金屬雙邊二次電子倍增已經(jīng)被廣泛研究.理論研究方面,Vaughan[1]建立了細(xì)致的動(dòng)力學(xué)理論模型并得到了聚焦相位條件;Lau等[2]給出了共振方程并據(jù)此給出了雙邊二次電子倍增敏感曲線;Kishek建立了電子面片簡(jiǎn)化模型[3]并發(fā)現(xiàn)了ping-pong類型二次電子倍增的存在[4].數(shù)值模擬方面,國(guó)內(nèi)外大多數(shù)工作采用了基于粒子軌跡跟蹤的蒙特卡羅方法,對(duì)不同領(lǐng)域的二次電子倍增敏感區(qū)間進(jìn)行預(yù)估和相關(guān)分析,由于蒙特卡羅方法并未考慮二次電子倍增過程中的空間電荷效應(yīng),因此無法獲得完整的物理圖像和深入認(rèn)識(shí)[5?9].Riyopoulos[10]討論了空間電荷效應(yīng)對(duì)雙邊二次電子倍增的影響,并認(rèn)為空間電荷效應(yīng)是導(dǎo)致雙邊二次電子倍增飽和的物理機(jī)制.

針對(duì)雙邊二次電子倍增的大多數(shù)研究,均是建立在射頻電壓幅值不隨負(fù)載電流變化的假設(shè)條件下的.Kishek[2,3]建立了射頻電壓幅值隨負(fù)載電流變化的等效電路模型,并在場(chǎng)已經(jīng)加載完畢的假設(shè)基礎(chǔ)之上,采用單能電子面片簡(jiǎn)化方法,對(duì)雙平板結(jié)構(gòu)腔體的二次電子倍增行為進(jìn)行了開創(chuàng)性研究工作.研究發(fā)現(xiàn):對(duì)于雙平板結(jié)構(gòu)的二次電子倍增,空間電荷效應(yīng)并不是二次電子倍增飽和的惟一機(jī)制,腔體結(jié)構(gòu)的加載效應(yīng)是不可忽略的.Kishek后來又將單一電流片模型推廣到兩個(gè)電流片,借此說明了空間電荷間的互相排斥現(xiàn)象,并發(fā)現(xiàn)了相位聚焦機(jī)制.隨后,Gopinath等[11]用一維粒子模擬(PIC)代碼進(jìn)行的數(shù)值模擬結(jié)果證實(shí)了Kishek的結(jié)論.事實(shí)上,Kishek的模擬結(jié)果已被實(shí)驗(yàn)所證實(shí).實(shí)驗(yàn)上發(fā)現(xiàn),高Q值諧振腔較慢的反應(yīng)時(shí)間和高儲(chǔ)能特性會(huì)導(dǎo)致能量注入方面的一些困難,老練時(shí)間會(huì)相當(dāng)長(zhǎng).一旦電壓到達(dá)二次電子倍增區(qū)間,二次電子倍增將鎖定在該電壓并且持續(xù)消耗注入腔體的能量.高Q值腔體可能會(huì)導(dǎo)致較大的二次電子倍增電流.而實(shí)際上,通常需要花費(fèi)數(shù)小時(shí)甚至幾天時(shí)間進(jìn)行腔體老練,最終才能使得腔體加載電壓達(dá)到設(shè)計(jì)電壓水平.

加速器動(dòng)態(tài)建場(chǎng)環(huán)節(jié)中,腔內(nèi)射頻電壓的建立是一個(gè)從無到有、逐步增長(zhǎng)的過程,高Q值腔體(超導(dǎo)腔)需要較長(zhǎng)的場(chǎng)加載時(shí)間,一般情況下為幾百個(gè)到數(shù)萬個(gè)射頻周期.因此,二次電子倍增形成后,其有足夠的時(shí)間發(fā)展到飽和階段.加速器建場(chǎng)過程中,若存在較為嚴(yán)重二次電子倍增現(xiàn)象,不僅會(huì)限制腔內(nèi)儲(chǔ)能,影響共振頻率,甚至?xí)?dǎo)致建場(chǎng)失敗[12?14].如:超導(dǎo)直線加速器中的二次電子倍增行為會(huì)嚴(yán)重影響其運(yùn)行穩(wěn)定性;超導(dǎo)回旋加速器內(nèi),雜散場(chǎng)的存在將會(huì)引起較強(qiáng)的二次電子倍增效應(yīng),其可能導(dǎo)致射頻場(chǎng)無法建立.上述工作中大多數(shù)為實(shí)驗(yàn)研究,雖然都發(fā)現(xiàn)了“高Q值腔體”內(nèi)的二次電子倍增現(xiàn)象會(huì)引發(fā)射頻腔建場(chǎng)的失敗,但是并沒有分析相關(guān)的物理機(jī)理.國(guó)內(nèi)針對(duì)加速器腔體二次電子倍增也開展了大量研究工作,但是大多數(shù)關(guān)心的是具體工程問題的解決方法,例如:中國(guó)科學(xué)院高能物理研究所對(duì)ADS項(xiàng)目超導(dǎo)腔中可能發(fā)生的二次電子倍增進(jìn)行了模擬計(jì)算[15],中國(guó)原子能研究院開發(fā)了加速器腔體內(nèi)二次電子倍增預(yù)測(cè)程序[16].

研究射頻場(chǎng)加載條件下的二次電子倍增行為時(shí),射頻電場(chǎng)是從零開始增長(zhǎng)的動(dòng)態(tài)過程,二次電子倍增與射頻場(chǎng)加載是一個(gè)相互影響、相互制約的復(fù)雜非線性物理過程,以往的簡(jiǎn)化模型將不再適用.我們借鑒Kim和Verboncoeur[17]針對(duì)介質(zhì)窗二次電子倍增的粒子模擬思路,前期采用粒子模擬方法細(xì)致研究了腔體雙邊二次電子倍增的瞬態(tài)及飽和特性以及材料二次電子發(fā)射特性對(duì)雙邊二次電子倍增的影響[18,19].在前期工作的基礎(chǔ)之上,本文通過建立射頻平板腔動(dòng)態(tài)建場(chǎng)等效電路以及腔體雙邊二次電子倍增的混合物理模型,編制了1D3V-PIC二次電子倍增和射頻平板腔動(dòng)態(tài)建場(chǎng)全電路互作用過程分析的程序,研究了二次電子倍增對(duì)射頻平板腔建場(chǎng)階段影響的全物理過程.不同于Kishek關(guān)注的腔體在穩(wěn)態(tài)加載條件下二次電子倍增的飽和過程和物理機(jī)制,我們既關(guān)心射頻場(chǎng)從無到有直至穩(wěn)態(tài)飽和的整個(gè)動(dòng)態(tài)建立過程,也關(guān)注二次電子倍增動(dòng)態(tài)演化發(fā)展對(duì)射頻建場(chǎng)過程的影響,包括:射頻場(chǎng)是否能夠建立,建場(chǎng)腔體電壓時(shí)域演化波形,二次電子電流時(shí)域發(fā)展波形以及腔體內(nèi)各種能量轉(zhuǎn)化過程和相互關(guān)系.

2 物理建模

本文選用雙平板結(jié)構(gòu)研究場(chǎng)加載過程中的二次電子倍增效應(yīng),一是因?yàn)閷?shí)際的加速器腔體會(huì)出現(xiàn)類似的結(jié)構(gòu)和場(chǎng)強(qiáng)分布,如:pillbox腔主要工作模式TM010與雙平板場(chǎng)強(qiáng)分布形式基本相同,spoke腔和crab腔的場(chǎng)強(qiáng)分布也都類似于雙平板場(chǎng)強(qiáng)分布形式;二是采用雙平板結(jié)構(gòu)易于實(shí)現(xiàn)可計(jì)算物理建模,對(duì)實(shí)際復(fù)雜構(gòu)型腔體的二次電子倍增過程進(jìn)行模擬費(fèi)時(shí)耗力,且不易俘獲二次電子倍增的微觀演化過程和發(fā)展飽和特性.不失一般性的前提下,我們采用雙平板簡(jiǎn)化模型,并以此構(gòu)型研究不同模式下的腔體雙邊二次電子倍增瞬時(shí)演化及飽和的全物理過程.

要研究射頻平板腔建場(chǎng)與二次電子倍增的復(fù)雜非線性自洽互作用過程,必須建立外電路與二次電子倍增動(dòng)力學(xué)耦合模型,將二次電子倍增作為外電路的一個(gè)動(dòng)態(tài)負(fù)載器件,才能進(jìn)行相關(guān)復(fù)雜物理過程的研究.射頻平板腔動(dòng)態(tài)建場(chǎng)過程中的二次電子倍增“場(chǎng)路”互作用物理模型.如圖1所示.

射頻平板腔雙邊二次電子倍增模型(“場(chǎng)”模型)如圖1(a)所示.間距為D的腔體中,初始電子在射頻電壓Ug作用下,從腔體下側(cè)壁面發(fā)射,受射頻場(chǎng)加速而獲得能量,經(jīng)過奇數(shù)個(gè)半射頻周期后轟擊腔體上側(cè)壁面,激發(fā)出多于初始電子數(shù)目的二次電子;產(chǎn)生的二次電子同樣在射頻場(chǎng)作用下經(jīng)過同樣時(shí)間轟擊腔體下側(cè)壁面,再次激發(fā)出更多的新的二次電子.如此往復(fù),便會(huì)出現(xiàn)二次電子倍增效應(yīng)(二次電子崩).

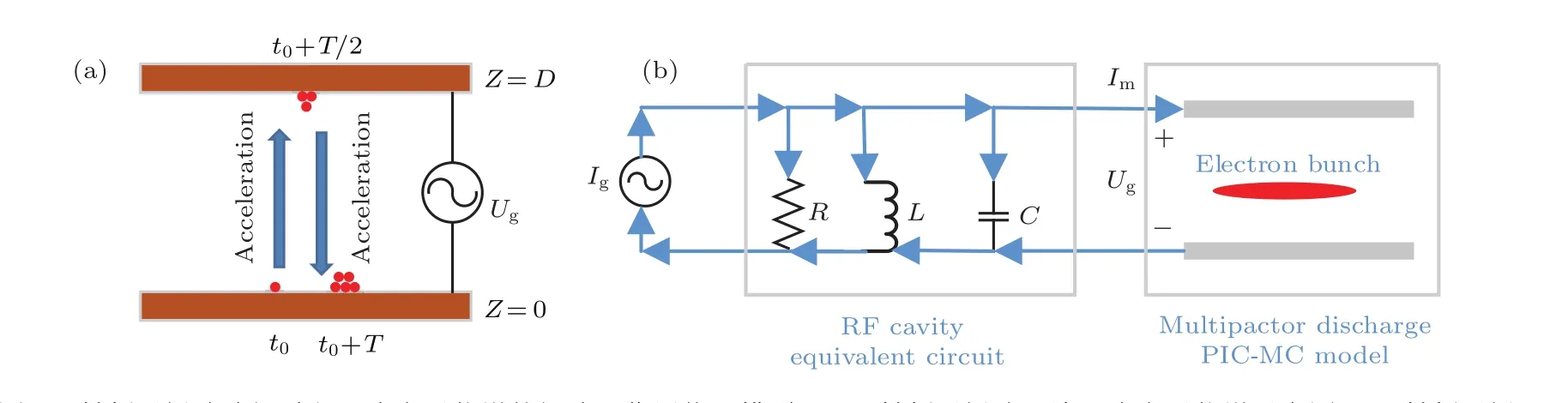
圖1 射頻平板腔建場(chǎng)過程二次電子倍增的場(chǎng)路互作用物理模型 (a)射頻平板腔雙邊二次電子倍增示意圖;(b)射頻平板腔建場(chǎng)等效電路圖Fig.1.Schematic of the field-circuit interactive-model of multipactor discharge during the field-buildup in radio frequency(RF)plate cavity:(a)Schematic of two-sided multipacting in RF plate cavity;(b)schematic of equivalent circuit of field-buildup in RF plate cavity.

射頻平板腔體動(dòng)態(tài)建場(chǎng)過程模型(“路”模型)如圖1(b)所示.射頻平板腔建場(chǎng)過程即為腔體儲(chǔ)能建立的過程,因此可等效為電流源驅(qū)動(dòng)的并聯(lián)RLC電路.其中Ig為腔體注入射頻信號(hào)電流源,Ig=Ig0sin(ωt),Ig0為電流源幅值,ω=2πf,f為射頻信號(hào)頻率;對(duì)于射頻電路,流通電阻R、電感L和電容C的電流分別設(shè)為IR,IL和IC;Im為腔體二次電子倍增形成的電流;Ug為腔體加載電壓(腔壓).

協(xié)同計(jì)算步驟如下:對(duì)于腔體二次電子倍增過程我們使用基于射頻場(chǎng)的粒子模擬與蒙特卡羅抽樣方法(PIC-MC)進(jìn)行求解,腔壓Ug(t)為輸入?yún)?shù),Im(t)為輸出量,粒子模擬統(tǒng)計(jì)獲得每一個(gè)時(shí)間步的二次電子電流Im;對(duì)于電路模型需要聯(lián)立求解二次電子電路和RLC電路,Im(t)為輸入量,腔壓Ug(t)則為輸出量.通過上述“場(chǎng)路協(xié)同”的計(jì)算方式,就可以自洽求解射頻平板腔動(dòng)態(tài)建場(chǎng)過程中的二次電子倍增非線性物理過程.需要說明的是:不同于Kishek[3]建立的穩(wěn)態(tài)模型,我們建立的模型中腔壓Ug(t)是從無到有直至穩(wěn)態(tài)飽和的動(dòng)態(tài)過程,在此動(dòng)態(tài)過程中研究二次電子倍增與射頻平板腔的非線性互作用.

2.1 描述射頻平板腔動(dòng)態(tài)建場(chǎng)過程的等效電路方程

根據(jù)基爾霍夫定律,圖1(b)所示的射頻平板腔動(dòng)態(tài)建場(chǎng)全電路模型可以寫為如下方程組:

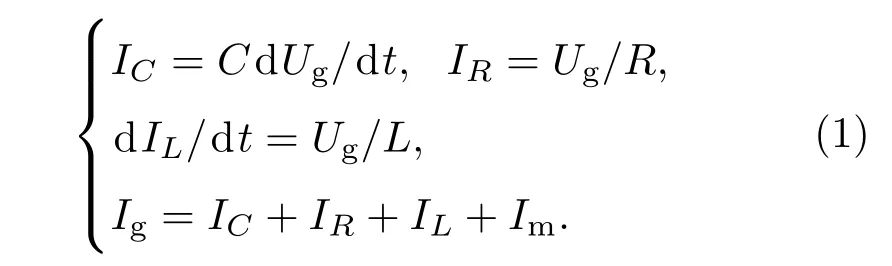
方程組(1)可以化簡(jiǎn)為如下二階微分方程:

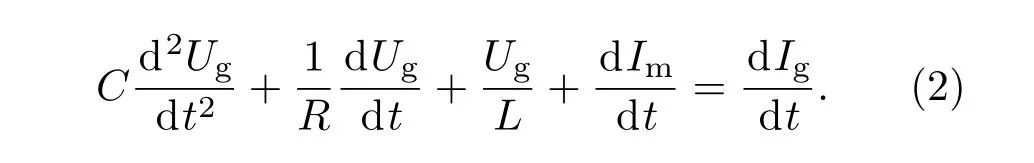
進(jìn)一步對(duì)(2)式化簡(jiǎn),可以獲得最終的全電路微分方程:

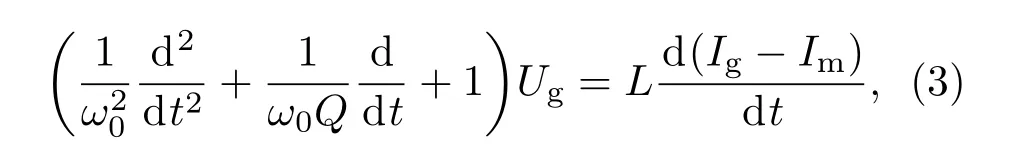
并聯(lián)RLC電路的R,L,C參數(shù),可通過下列方法求解:

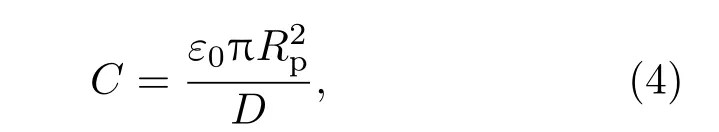
其中ε0為真空介電常數(shù),Rp為平板腔體的上下平板半徑,D為射頻平板腔上下板間距.

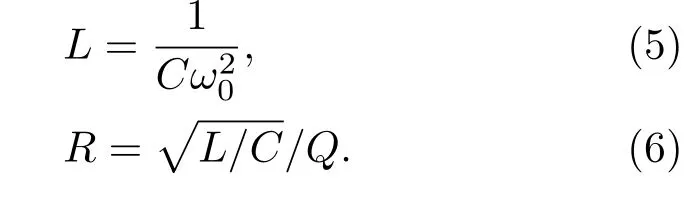
2.2 二次電子動(dòng)力學(xué)方程與粒子模擬方法

粒子模擬中考慮了射頻場(chǎng)與帶電粒子產(chǎn)生的空間電荷場(chǎng)對(duì)粒子的雙重作用,并通過求解外電路互作用方程實(shí)現(xiàn)腔體動(dòng)態(tài)加載效應(yīng)的自洽模擬(即考慮了射頻電壓幅值Ug與外電路聯(lián)動(dòng)的動(dòng)態(tài)變化).

二次電子動(dòng)力學(xué)方程如下:

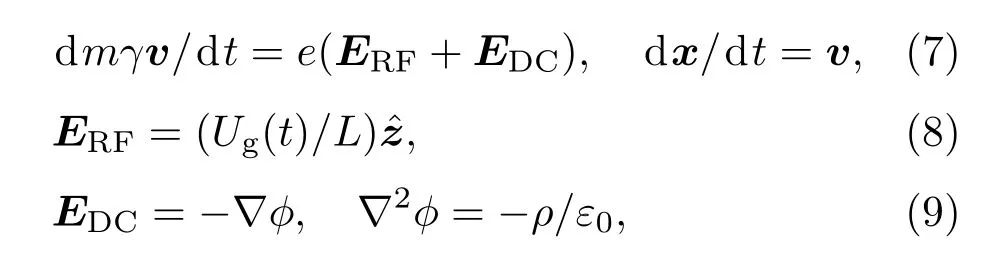
ERF,EDC分別為射頻電場(chǎng)強(qiáng)度矢量和電子產(chǎn)生的空間電荷場(chǎng)強(qiáng)度矢量;v,x,e和γ分別為電子速度矢量、位移矢量、電量和相對(duì)論因子;?,ρ分別為空間電荷靜電勢(shì)與電荷密度;?z為z方向單位矢量.EDC定義在網(wǎng)格中心;?,ρ定義在網(wǎng)格結(jié)點(diǎn)位置.使用cloud-in-cell(CIC)方法(線性插值PIC)將EDC權(quán)重到粒子位置,同樣方法將粒子電量權(quán)重到網(wǎng)格結(jié)點(diǎn)位置得出ρ.泊松方程可通過追趕法(一維情況)或松弛迭代求解(二維情況),?求解后,通過中心差分求解可得EDC.我們編制了1D3V(一維三速)和2D3V(二維三速)PIC(粒子模擬)程序.由于1D3V程序計(jì)算速度遠(yuǎn)快于2D3V程序,通過2D3V與1D3V程序模擬結(jié)果的比對(duì),在完成1D3V程序正確性驗(yàn)證后,主要使用二次電子倍增1D3V-PIC程序和射頻平板腔動(dòng)態(tài)建場(chǎng)全電路程序進(jìn)行協(xié)同計(jì)算,研究射頻平板腔建場(chǎng)過程與二次電子倍增的互作用物理規(guī)律.

2.3 材料二次電子發(fā)射模型

腔體內(nèi)表面二次電子產(chǎn)生過程的建模,采用Vaughan[20]提出的二次電子產(chǎn)額經(jīng)驗(yàn)擬合公式:

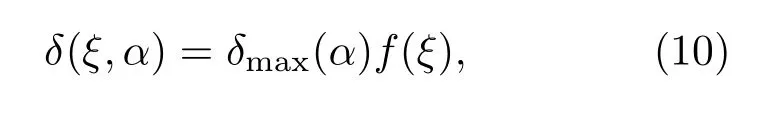
式中

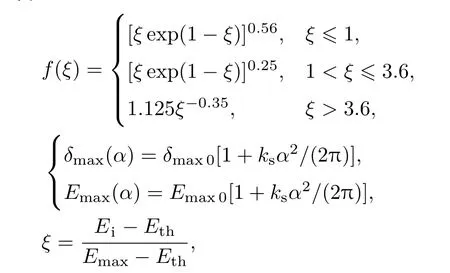
δ為二次電子產(chǎn)額(secondary electron yield,SEY)系數(shù);δmax0為正入射二次電子產(chǎn)額系數(shù)最大值;Emax0為δmax0對(duì)應(yīng)的入射能量;α為入射角(α=0為正入射,α= π/2為掠入射);δmax(α)為入射角為α?xí)r二次電子產(chǎn)額系數(shù)最大值;Emax(α)為δmax(α)對(duì)應(yīng)的入射能量;ks為表面光滑系數(shù)(ks=0,1,2,分別代表粗糙、不光滑和光滑).Ei為電子碰撞能量;Eth為能量閾值,一般取Eth=12.5 eV.δ＞1對(duì)應(yīng)的碰撞能量分布范圍(E1＜Ei＜E2,E1為二次電子倍增的碰撞能量下限值,E2為上限值)為材料二次電子倍增區(qū)間,其代表此區(qū)間內(nèi)每個(gè)種子電子碰撞產(chǎn)生的二次電子數(shù)目大于1.加速器腔體一般采用的是無氧銅材料,對(duì)于無氧銅材料:ks=1,δmax0=1.3,Emax0=600 eV.后續(xù)數(shù)值模擬中采用該參數(shù).

二次電子初始能量概率密度函數(shù)滿足[21]f(E0)=(E0/E20m)exp(?E0/E0m),其中E0為二次電子出射能量,E0m是函數(shù)f(E0)峰值所對(duì)應(yīng)的二次電子出射能量,E0m取值與材料特性有關(guān),根據(jù)Vaughan的constant-k理論,一般取E0m=0.005Emax0.二次電子發(fā)射角?是偏離平行出射表面方向的角度,其概率密度函數(shù)g(?)滿足[21]g(?)=0.5sin(?),?取值范圍為0＜?＜π.這里采用蒙特卡羅(MC)方法對(duì)二次電子的出射能量和角度進(jìn)行隨機(jī)抽樣.

3 模擬結(jié)果分析討論

為了配合后續(xù)的實(shí)驗(yàn)研究和相關(guān)驗(yàn)證工作,粒子模擬中設(shè)置射頻頻率f=72 MHz,平板腔體的上下平板半徑Rp=7.5 cm,射頻平板腔上下板間距D=4 cm,對(duì)應(yīng)頻率間距積fD=0.288 GHz·cm,假設(shè)二次電子發(fā)射面積分為S=4.42 cm2或S=8.84 cm2兩種情況,背景種子電子電流密度10μA/cm2(位置隨機(jī)出現(xiàn)在腔體兩側(cè)壁面).腔體諧振頻率f0=72 MHz,腔體Q值分為Q=6000或Q=4000兩種情況;無二次電子倍增條件下,設(shè)置建場(chǎng)成功后腔壓Ug的穩(wěn)態(tài)幅值為20 kV.使用二分法測(cè)算獲得腔體Q=6000情況下的驅(qū)動(dòng)電流源幅值Ig0=5.9 mA;腔體Q=4000情況下的驅(qū)動(dòng)電流源幅值Ig0=8.85 mA.

使用自編的二次電子倍增1D3V-PIC程序和射頻平板腔動(dòng)態(tài)建場(chǎng)全電路程序進(jìn)行協(xié)同計(jì)算,數(shù)值模擬研究了射頻平板腔建場(chǎng)過程中二次電子倍增及其對(duì)動(dòng)態(tài)建場(chǎng)過程的影響.模擬結(jié)果如圖2–圖7所示.

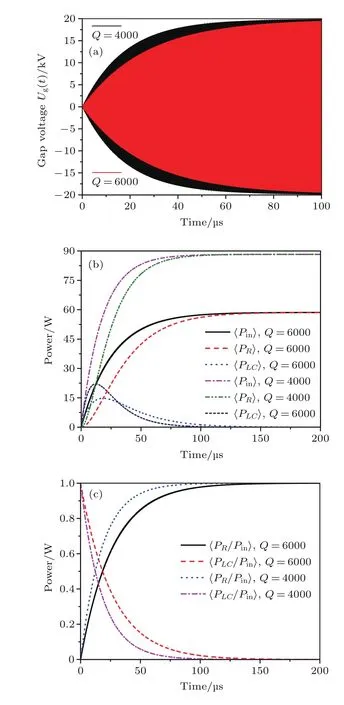
圖2 不同腔體Q值情況下間隙電壓演化及腔內(nèi)功率轉(zhuǎn)換關(guān)系(無二次電子倍增) (a)間隙電壓隨時(shí)間演化關(guān)系;(b)系統(tǒng)內(nèi)各功率隨時(shí)間演化關(guān)系;(c)系統(tǒng)內(nèi)各功率間轉(zhuǎn)換關(guān)系Fig.2. Evolutionsofgap-voltageand powerinterchange under the condition of cavity with different Q-values(no multipacting):(a)Gap voltage vs.time;(b)power in system vs.time;(c)power interchange in system.

首先研究了無二次電子倍增情況下腔體順利完成建場(chǎng)的物理過程,如圖2所示.從圖2(a)可以看出:腔體電壓Ug從0 V建立到20 kV是一個(gè)非常緩慢的過程,且腔體Q值越高,建場(chǎng)時(shí)間越長(zhǎng),Q=4000時(shí)建場(chǎng)時(shí)間大約需要100μs,Q=6000時(shí)建場(chǎng)時(shí)間則需要150μs左右.圖2(b)中〈〉代表以射頻周期進(jìn)行平均,〈Pin〉表示注入系統(tǒng)總功率平均值,〈Pin〉=〈IgUg〉;〈PR〉代表腔體消耗功率平均值,〈PR〉=〈IRUg〉;〈PLC〉表示腔體電磁儲(chǔ)能功率平均值,〈PLC〉=〈ILUg+ICUg〉. 從圖2(b)可以看出:系統(tǒng)內(nèi)的能量/功率是相互轉(zhuǎn)換的,〈Pin〉=〈PR〉+〈PLC〉.〈Pin〉是緩慢增加到穩(wěn)態(tài)飽和值,飽和時(shí)間與建場(chǎng)時(shí)間相等;〈PR〉也是呈現(xiàn)緩慢增加到穩(wěn)態(tài)飽和值的規(guī)律,且飽和時(shí)〈PR〉=〈Pin〉,腔體消耗功率平均值上升階段〈PR〉＜〈Pin〉,說明建場(chǎng)完畢(Ug進(jìn)入穩(wěn)態(tài)飽和階段)前,注入系統(tǒng)的能量除了腔體消耗外,其余部分的能量轉(zhuǎn)化為腔體電磁儲(chǔ)能;〈PLC〉是先增加再降低最后歸零的過程,前半段〈PLC〉＞〈PR〉表明此階段儲(chǔ)能速度快于耗能速度,后半段〈PLC〉＜〈PR〉表明此階段耗能速度快于儲(chǔ)能速度,建場(chǎng)完畢(Ug進(jìn)入穩(wěn)態(tài)飽和階段)后〈PLC〉=0,說明此時(shí)腔體儲(chǔ)能已達(dá)飽和,注入能量等于腔體消耗能量.腔體Q值大小主要影響注入能量速度、儲(chǔ)能速度和能量消耗速度;腔體Q值越高能量注入速度、儲(chǔ)能速度和能量消耗速度越慢.從圖2(c)可以看出:隨時(shí)間演進(jìn),平均儲(chǔ)能功率占平均注入功率的比重是下降的,平均消耗功率占平均注入功率的比重是上升的;且腔體Q值越高,對(duì)應(yīng)的下降速度和上升速度越慢.

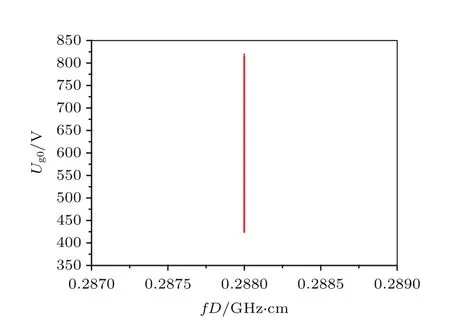
圖3 雙邊二次電子倍增敏感區(qū)間Fig.3.Susceptibility of two-sided multipacting.

利用蒙特卡羅方法計(jì)算了腔體雙邊二次電子倍增的敏感區(qū)間,如圖3所示.可以看出,對(duì)于射頻頻率f=72 MHz,腔體間距D=4 cm,即頻率間距積fD=0.288 GHz·cm情況下,引發(fā)二次電子倍增的腔壓幅值Ug0的范圍大約是400–800 V.圖4給出了不同腔體Q值情況下,對(duì)應(yīng)腔壓幅值400–800 V范圍內(nèi)的二次電子倍增作用時(shí)間間隔.可以看出,腔體Q值較低情況下,進(jìn)入二次電子倍增的時(shí)刻早,作用時(shí)間短;腔體Q值較高的情況下,進(jìn)入二次電子倍增的時(shí)刻晚,作用時(shí)間長(zhǎng).需要說明的是,圖4腔壓時(shí)域波形是在無二次電子倍增情況下給出的,僅為簡(jiǎn)述作用時(shí)間概念,并未考慮二次電子倍增對(duì)腔壓的影響.二次電子倍增作用時(shí)間間隔越長(zhǎng),二次電子倍增就有足夠的時(shí)間發(fā)展到飽和狀態(tài),飽和階段的二次電子數(shù)目更多,二次電子電流也會(huì)更大,較大的二次電子電流將會(huì)起到明顯的分流作用,導(dǎo)致加載腔壓的降低,最終有可能導(dǎo)致射頻建場(chǎng)的失敗.

其次,研究了二次電子倍增對(duì)射頻平板腔動(dòng)態(tài)建場(chǎng)過程的影響.圖5給出了不同腔體Q值、不同二次電子發(fā)射面積情況下發(fā)生二次電子倍增時(shí)電流源、間隙電壓、放電電流的時(shí)域波形,可以從腔壓Ug的時(shí)域波形判斷射頻平板腔是否建場(chǎng)成功.

圖5(a)是Q=4000,S=4.42 cm2情況下的建場(chǎng)物理圖像.可以看出,隨著電流源Ig的驅(qū)動(dòng),腔壓Ug從零開始增加,大約到0.5μs左右(對(duì)應(yīng)腔壓幅值400 V)進(jìn)入了二次電子倍增區(qū)間,此時(shí)由于二次電子倍增效應(yīng)引發(fā)的分流作用,腔壓開始進(jìn)入緩慢增長(zhǎng)階段(0.5–1.0μs),1.0μs以后由于腔壓幅值已脫離二次電子敏感區(qū)間上限(800 V),所以二次電子電流消失,之后腔壓繼續(xù)增加,建場(chǎng)成功.在二次電子倍增區(qū)域時(shí)段(0.5–1.0μs),二次電子電流呈現(xiàn)脈沖形狀,其幅值略小于驅(qū)動(dòng)電流源幅值Ig0.

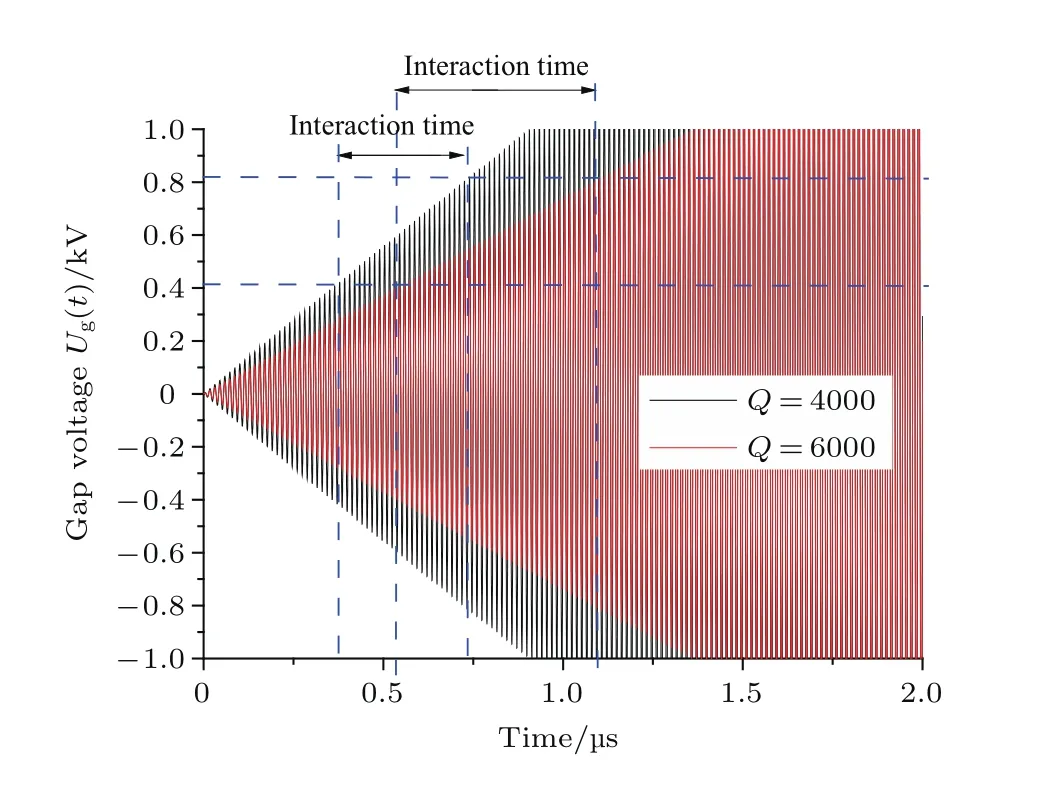
圖4 二次電子倍增間隙電壓范圍及作用間隔Fig.4.Amplitude of gap-voltage and interaction time during multipacting.

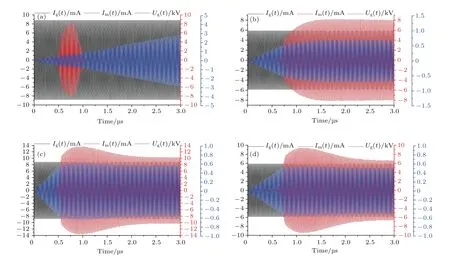
圖5 不同腔體Q值情況下電流源、間隙電壓、放電電流時(shí)域波形(發(fā)生二次電子倍增) (a)Q=4000,S=4.42 cm2;(b)Q=6000,S=4.42 cm2;(c)Q=4000,S=8.84 cm2;(d)Q=6000,S=8.84 cm2Fig.5.Waveforms of Ig,Ugand Imunder the condition of cavity with different Q-values(with multipacting interaction):(a)Q=4000,S=4.42 cm2;(b)Q=6000,S=4.42 cm2;(c)Q=4000,S=8.84 cm2;(d)Q=6000,S=8.84 cm2.

圖5(b)是Q=6000,S=4.42 cm2情況下的建場(chǎng)物理圖像.可以看出,隨著電流源Ig的驅(qū)動(dòng),腔壓Ug從零開始增加,大約到0.75μs(對(duì)應(yīng)腔壓幅值400 V)進(jìn)入了二次電子倍增區(qū)間,此時(shí)由于二次電子倍增效應(yīng)引發(fā)的分流作用,腔壓開始進(jìn)入緩慢增長(zhǎng)階段(0.75–1.5μs),1.5μs以后二次電子電流幅值增加到大于驅(qū)動(dòng)電流源幅值Ig0,較強(qiáng)的二次電子倍增分流電流限制了腔壓的進(jìn)一步上升,腔壓幅值隨后維持750 V左右不變,建場(chǎng)失敗.

圖5(c)是Q=4000,S=8.84 cm2情況下的建場(chǎng)物理圖像,可以看出:隨著電流源Ig的驅(qū)動(dòng),腔壓Ug從零開始增加,大約到0.5μs(對(duì)應(yīng)腔壓幅值400 V)進(jìn)入了二次電子倍增區(qū)間,此時(shí)由于二次電子倍增效應(yīng)引發(fā)的分流作用,腔壓開始進(jìn)入緩慢增長(zhǎng)階段(0.5–1.0μs),二次電子電流幅值增加到大于驅(qū)動(dòng)電流源幅值Ig0,較強(qiáng)的二次電子倍增分流電流限制了腔壓的進(jìn)一步上升;1.0μs以后,二次電子電流開始有所減小并趨于穩(wěn)定,腔壓幅值緩慢下降后維持在600 V左右不變,建場(chǎng)失敗.

圖5(d)是Q=6000,S=8.84 cm2情況下的建場(chǎng)物理圖像.可以看出,隨著電流源Ig的驅(qū)動(dòng),腔壓Ug從零開始增加,大約到0.75μs(對(duì)應(yīng)腔壓幅值400 V)進(jìn)入了二次電子倍增區(qū)間,隨后二次電子電流幅值很快增加到大于驅(qū)動(dòng)電流源幅值Ig0,較強(qiáng)的二次電子倍增分流電流限制了腔壓的進(jìn)一步上升;0.75μs以后,腔壓幅值就不能繼續(xù)增加,而是維持在500 V左右不變,此時(shí)二次電子電流開始減小并趨于穩(wěn)定,建場(chǎng)失敗.

綜上,由于二次電子束流負(fù)載的作用,射頻電壓幅值會(huì)隨著負(fù)載電流的變化而改變,導(dǎo)致二次電子倍增電子電流飽和的主要機(jī)制是:束流負(fù)載電流的增加使射頻電壓幅值降低,從而使電子碰撞能量降低,二次電子電流停止增長(zhǎng).二次電子發(fā)射面積相同的情況下,腔體Q值越高,二次電子倍增作用時(shí)間越長(zhǎng),越容易導(dǎo)致建場(chǎng)失敗,最終鎖定的腔壓幅值越低;腔體Q值相同的情況下,二次電子發(fā)射面積越大,二次電子電流峰值越高,越容易導(dǎo)致建場(chǎng)失敗,最終鎖定的腔壓幅值越低.

圖6給出了不同腔體Q值、不同二次電子發(fā)射面積情況下發(fā)生二次電子倍增時(shí)系統(tǒng)內(nèi)各平均功率間的相互轉(zhuǎn)換關(guān)系,〈Pm/Pin〉表示平均二次電子放電功率占平均注入功率的比重,〈PRLC/Pin〉表示平均儲(chǔ)能功率與平均消耗功率之和占平均注入功率的比重.可以看出:平均注入功率等于平均儲(chǔ)能功率、平均消耗功率以及平均二次電子放電功率三者之和,即〈Pm/Pin〉+〈PRLC/Pin〉=1.

腔體Q值較低以及二次電子發(fā)射面積較小情況下,二次電子倍增放電功率為短脈沖形式(脈沖持續(xù)從0.5μs開始到1.0μs結(jié)束),對(duì)應(yīng)〈PRLC/Pin〉為一個(gè)反脈沖,加載腔壓突破二次電子倍增區(qū)間上限電壓幅值后,二次電子倍增消失,〈Pm/Pin〉=0,〈PRLC/Pin〉=1.腔體Q值較高但二次電子發(fā)射面積較小情況下,二次電子倍增放電功率呈現(xiàn)增加直至穩(wěn)定的規(guī)律(＞ 0.75μs),對(duì)應(yīng)〈PRLC/Pin〉呈現(xiàn)減小直至穩(wěn)定的規(guī)律,最終〈Pm/Pin〉=1,〈PRLC/Pin〉=0.二次電子發(fā)射面積較大情況下,二次電子倍增放電功率呈現(xiàn)先增加后減小最終穩(wěn)定的規(guī)律,出現(xiàn)了平均放電功率峰值大于平均注入功率的現(xiàn)象,即〈Pm/Pin〉＞1;對(duì)應(yīng)〈PRLC/Pin〉呈現(xiàn)先減小后增加直至穩(wěn)定的規(guī)律,〈PRLC/Pin〉最小值出現(xiàn)了小于零的現(xiàn)象(對(duì)應(yīng)〈Pm/Pin〉＞1的時(shí)間段),由于〈PR〉≥ 0,所以對(duì)應(yīng)〈PRLC/Pin〉＜0的時(shí)間段內(nèi)滿足〈PLC〉＜0,即出現(xiàn)了平均儲(chǔ)能功率小于零的現(xiàn)象(對(duì)外放能現(xiàn)象);由此說明,此時(shí)間段內(nèi)的二次電子倍增放電能量除了由注入能量提供之外,還消耗了部分腔體儲(chǔ)能進(jìn)行補(bǔ)償.

圖7給出了不同腔體Q值、不同二次電子發(fā)射面積情況下,發(fā)生二次電子倍增時(shí)二次電子數(shù)目隨時(shí)間的演進(jìn)過程.可以看出,腔體Q值較低以及二次電子發(fā)射面積較小的情況下,二次電子數(shù)目呈現(xiàn)快速增長(zhǎng)后迅速下降的短脈沖形狀,脈沖持續(xù)時(shí)間從0.5μs開始到1.0μs結(jié)束,后續(xù)未出現(xiàn)二次電子倍增,建場(chǎng)成功;腔體Q值較高但二次電子發(fā)射面積較小情況下,二次電子數(shù)目呈現(xiàn)快速增長(zhǎng)后趨于穩(wěn)定的規(guī)律;相對(duì)二次電子發(fā)射面積相同但腔體Q值較低的情況,二次電子倍增發(fā)生時(shí)間存在明顯的滯后;腔體Q值較低以及二次電子發(fā)射面積較大的情況下,二次電子數(shù)目呈現(xiàn)快速增長(zhǎng)后略有下降最終趨于穩(wěn)定的規(guī)律;腔體Q值較高以及二次電子發(fā)射面積較大情況下,二次電子數(shù)目也是呈現(xiàn)快速增長(zhǎng)后略有下降最終趨于穩(wěn)定的規(guī)律;相對(duì)二次電子發(fā)射面積相同但腔體Q值較低的情況,二次電子倍增發(fā)生時(shí)間存在明顯的滯后現(xiàn)象,二次電子數(shù)目更少.另外,腔體Q值相同的情況下,二次電子發(fā)射面積越大,二次電子數(shù)目峰值越高.

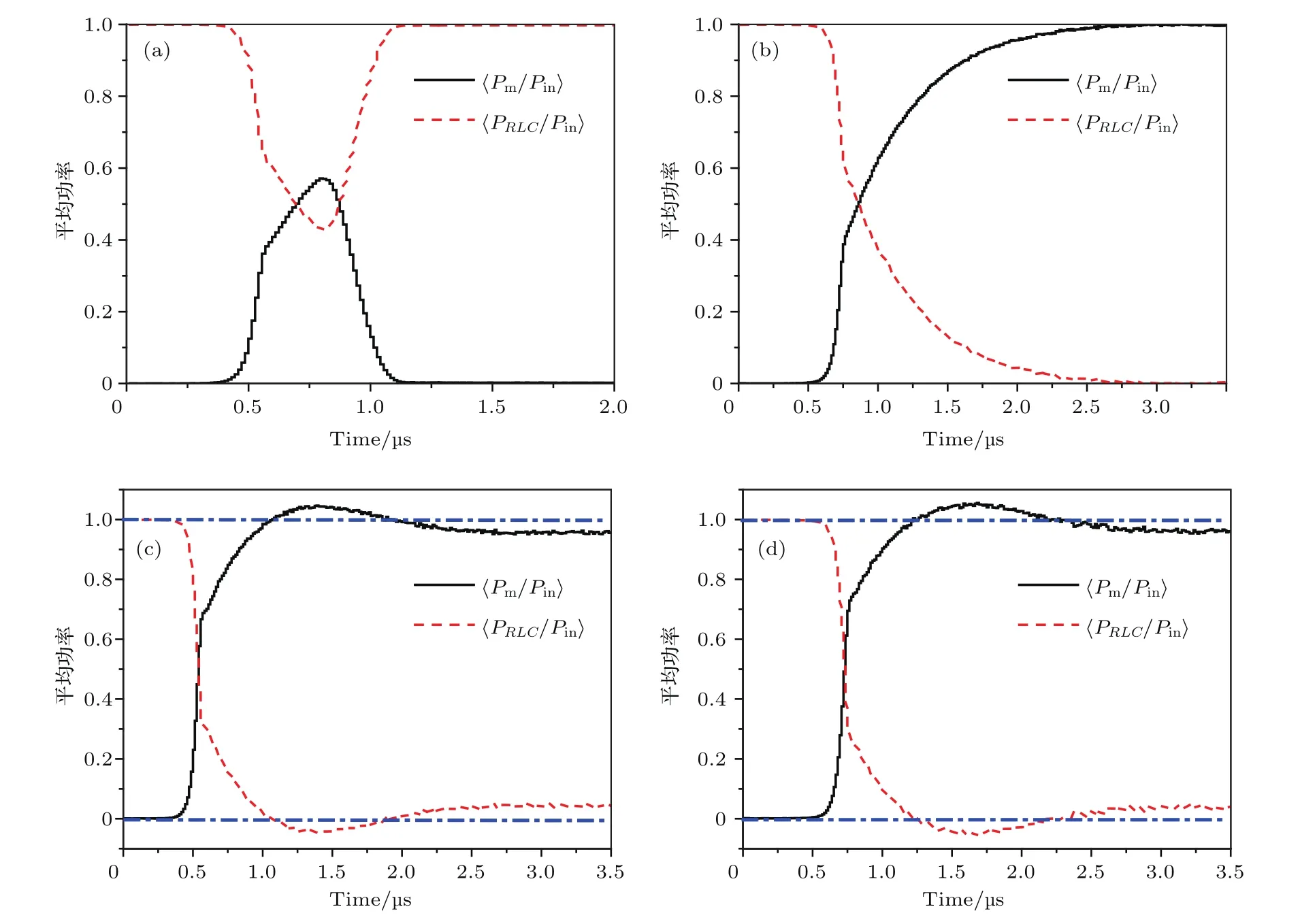
圖6 不同腔體Q值情況下系統(tǒng)內(nèi)各平均功率間的相互轉(zhuǎn)換關(guān)系(發(fā)生二次電子倍增) (a)Q=4000,S=4.42 cm2;(b)Q=6000,S=4.42 cm2;(c)Q=4000,S=8.84 cm2;(d)Q=6000,S=8.84 cm2Fig.6.Interchange-relationship of power under the condition of cavity with different Q-values(with multipacting interaction):(a)Q=4000,S=4.42 cm2;(b)Q=6000,S=4.42 cm2;(c)Q=4000,S=8.84 cm2;(d)Q=6000,S=8.84 cm2.

圖7 二次電子倍增過程中電子數(shù)目隨時(shí)間的演化關(guān)系 (a)S=4.42 cm2;(b)S=8.84 cm2Fig.7.The number of secondary electrons vs.time in multipactor discharge:(a)S=4.42 cm2;(b)S=8.84 cm2.

4 結(jié) 論

本文建立了射頻平板腔動(dòng)態(tài)建場(chǎng)等效電路以及腔體雙邊二次電子倍增的混合物理模型,包括:描述射頻平板腔動(dòng)態(tài)建場(chǎng)過程的等效電路方程,基于粒子模擬的腔體雙邊二次電子倍增動(dòng)力學(xué)方程以及基于蒙特卡羅抽樣的材料二次電子發(fā)射模型;編制了1D3V-PIC二次電子倍增程序和射頻平板腔動(dòng)態(tài)建場(chǎng)全電路程序,通過“場(chǎng)路”協(xié)同計(jì)算,研究了二次電子倍增對(duì)射頻平板腔建場(chǎng)階段影響的全物理過程,給出了腔壓、二次電子電流、平均注入功率、腔體消耗功率、腔體儲(chǔ)能功率等關(guān)鍵物理量的時(shí)域波形.模擬所得結(jié)論如下.

建場(chǎng)過程中不存在二次電子倍增情況下:腔體Q值越高,建場(chǎng)時(shí)間越長(zhǎng),系統(tǒng)內(nèi)的能量是相互轉(zhuǎn)換的,注入能量等于腔體儲(chǔ)能和腔體耗能;平均腔體消耗功率呈現(xiàn)持續(xù)增加到穩(wěn)定的趨勢(shì),平均腔體儲(chǔ)能功率呈現(xiàn)先增加再降低最后歸零的過程,建場(chǎng)前期腔體儲(chǔ)能速度快于耗能速度,建場(chǎng)后期腔體耗能速度快于儲(chǔ)能速度,建場(chǎng)成功后平均腔體消耗功率與平均注入功率相等;建場(chǎng)過程中,平均儲(chǔ)能功率占平均注入功率的比重是逐步下降的,最終趨于零,平均消耗功率占平均注入功率的比重逐步上升,最終趨于1.

建場(chǎng)過程中存在二次電子倍增情況下:保持腔體Q值不變,二次電子發(fā)射面積越大,二次電子數(shù)目越多,二次電子電流峰值越高,最終鎖定的腔壓幅值越低;保持二次電子發(fā)射面積不變,腔體Q值越高,進(jìn)入二次電子倍增的時(shí)刻越晚,二次電子倍增作用時(shí)間越長(zhǎng),二次電子數(shù)目越少,二次電子電流峰值越低,最終鎖定的腔壓幅值越低.二次電子倍增持續(xù)加載是導(dǎo)致射頻平板腔建場(chǎng)過程失敗的直接誘因;腔體Q值越高或二次電子發(fā)射面積越大,射頻平板腔建場(chǎng)失敗概率越高.二次電子電流飽和的主要機(jī)制是束流負(fù)載電流的增加使射頻電壓幅值降低,從而使電子碰撞能量降低,二次電子電流停止增長(zhǎng).

后續(xù)我們還將進(jìn)一步研究加速器建場(chǎng)過程中二次電子倍增的抑制方法和相關(guān)手段.