一類半線性分數Laplacian方程多解的存在性問題

喬花玲,吳玉梅

(西安財經學院統計學院,陜西西安 710061)

1 引言

分數Laplacian算子(?Δ)s的定義如下:

分數Laplacian算子(?Δ)s及更一般的擬微分算子已經有經典的泛函分析方法研究成果,該算子在連續介質力學、相變現象、種群動態、對策論的研究中常出現,它是Lévy過程的隨機穩定的無窮小生成元[2?4].由于分數空間和非局部方程在很多科學領域有著重要應用,在過去的幾年里對涉及分數算子問題的研究興趣仍不斷高漲,如障礙問題[5]、優化與金融[6,7]、共形幾何與極小曲面[8?10]、材料學[11]、反常擴散[12?14]等方面應用.

設n≥2,s∈(0,1),方程

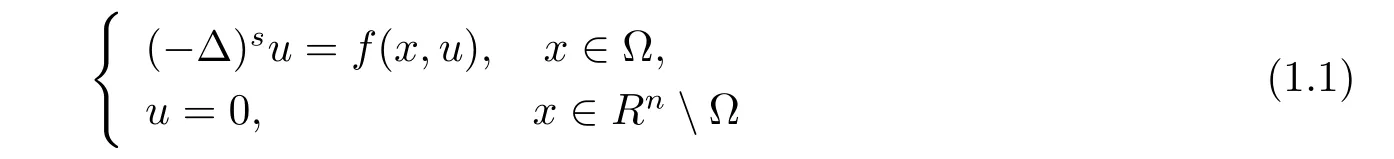
已經得到廣泛的關注.Rox-Oton和Serra[15]建立與(1.1)式相聯系的Pohozaev恒等式,并證明了在有界光滑的星型域上,若非線性項f(u)是局部的Lipschitz函數,有不等式

成立,則問題(1.1)沒有有界正解,當不等式嚴格成立時,問題(1.1)沒有非平凡的有界解;若在×R的任意緊子集上f(x,u)是Lipschitz函數,有不等式

成立,則問題(1.1)沒有有界正解,當不等式嚴格成立時,問題(1.1)沒有非平凡的有界解.Fall和Weth[16]給出了在有界星型域?(0∈)上,非線性項f(x,t):{0}×[0,∞)→R在{0}上的每一個子集上關于t是一致局部Lipschitz且在某種意義下是超臨界的,則問題(1.1)沒有正解,參見文獻[16,定理1.1].在無界的星型域上,當時,問題(1.1)沒有非平凡解.如果Fang[17]研究了帶有純臨界非線性項的Laplacian問題,在空間Ds,2(Rn)上,得出問題(1.1)有無窮多非徑向變號解;Gonzalez[18]等討論了該方程在雙曲空間上層解的存在性、對稱性;Servadei[19]等發現具有齊次Dirichlet邊界條件非局部微積分算子對應的方程有變分結構,利用山路定理證明了其非平凡解的存在性,此結果對一般的分數微積分算子也成立,作為其特殊情形證明了半線性橢圓問題(1.1)非線性項f:?×R→R是Carathéodory函數時,非平凡解的存在性;當s=時,Cabré[20]等研究了光滑有界域上正解的存在性,對問題(1.1)非平凡解研究已經有比較完善的結果了,關于問題(1.1)解的存在性等其它問題的許多結果請參考文獻[21–26].對于其是否有無窮解的研究結果為數不多.最近,Liu等[27]研究了如果f(x,u)是關于u的奇函數且滿足一定的增長條件,則經典的Dirichlet邊界值問題

有無窮多解uk,當k→∞時,有‖uk‖L∞→0.受此啟發,本文將研究半線性橢圓問題(1.1)多解的存在性.

設??Rn是具有光滑邊界的有界域,記

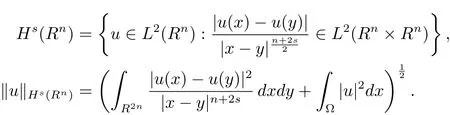
定義1.1若對任意?∈C∞(Rn),有

成立,則稱u(x)是問題(1.1)的弱解.

定義1.2設Φ∈C1(Hs(Rn)),稱Φ滿足PS條件是指:若任意序列滿足下列條件

(2)在Hs(Rn)上Φ′(uk)→0有收斂序列.

主要結果是

一致成立,則問題(1.1)有無窮多解uk,且當k→∞時,‖uk‖L∞→0,其中

本文安排如下:第2部分,驗證PS條件;第3部分,利用Clark’s定理證明定理1.1,并作為推廣,給出方程組多解的存在性.

2 驗證PS條件

為了證明主要結果,考慮問題

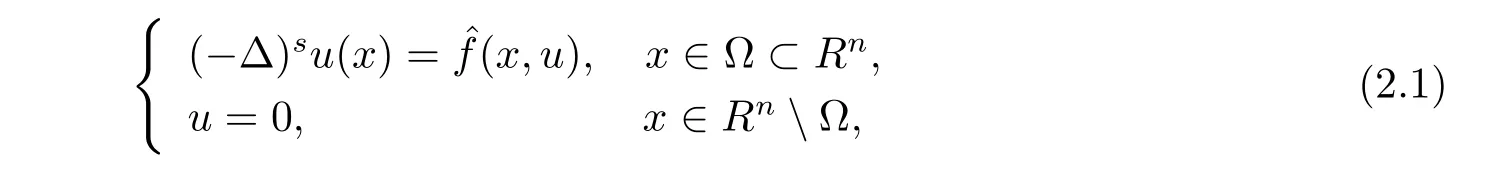
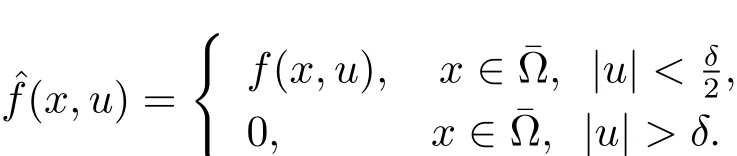
(2.1)式相應的泛函為

引理2.1 Φ(u)∈C1(Hs(Rn))是偶的,強制的且下有界.Z

由(1.3)式可得存在常數C1,使得,根據空間Hs(Rn)上范數的定義有

因此有

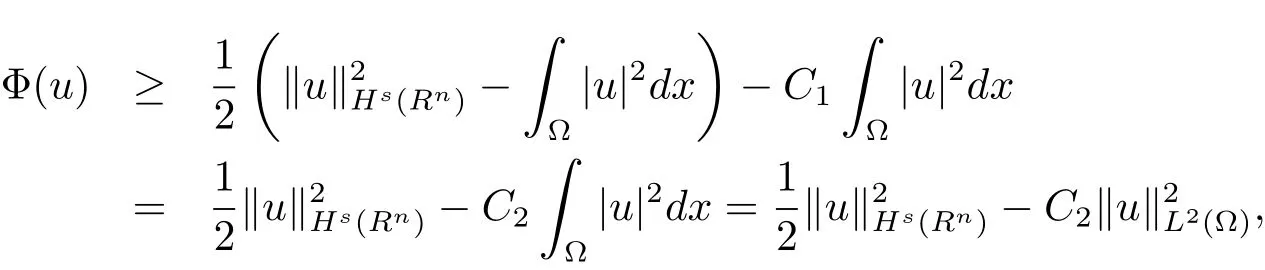
引理2.2若{un}在Hs(Rn)上弱收斂到u,則在Lq(Rn)上{un}滿足PS條件,其中

證 由Φ′的定義有

由 H?older不等式有

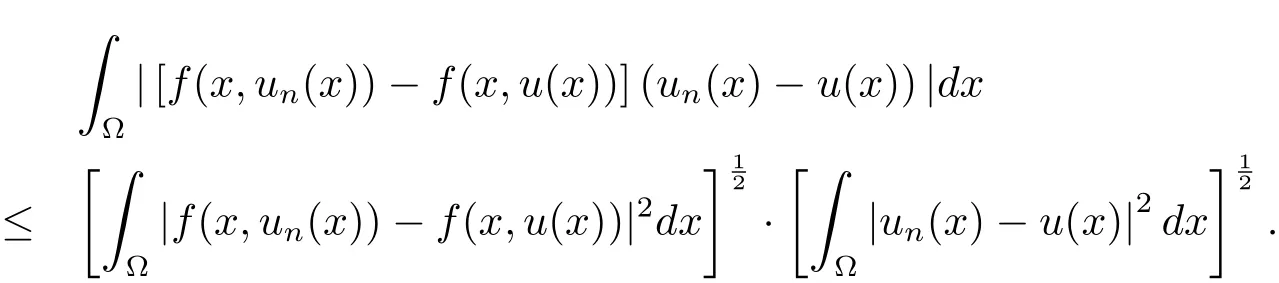
在Lq(Rn)上un(x)→u(x),映射t|→f(x,t)關于t連續,t∈R,所以

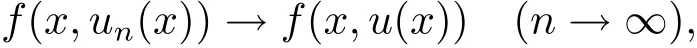
在?上a.e.成立.

由假設f(x,u(x))有界及控制收斂定理知

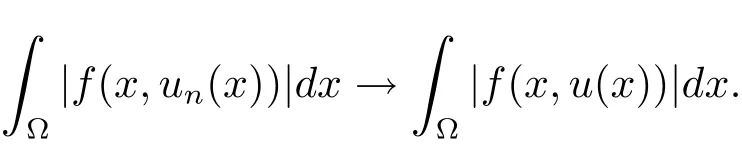
再由引理2.1知Φ(u)是強制的,故序列{un}是有界的,因此有

聯立(2.2)–(2.4)式可得

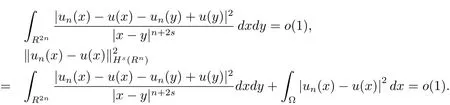
因此Φ(u)滿足PS條件.

3 定理1.1的證明

為了證明定理1.1,需要如下關鍵定理.

定理3.1 (見文獻[27])設X 是Banach空間,Φ∈C1(X,R),Φ是偶泛函,下有界且Φ(0)=0,滿足PS條件.如果對任意k∈N,存在X 的k-維子空間Xk及ρk＞0使得Φ＜0,其中Sρ={u∈X|‖u‖=ρ},那么下面的結論至少有一個成立:

1)存在臨界點序列{uk}滿足對任意的k,當k→∞ 時,‖uk‖→0,Φ(uk)＜0;

2)存在r＞0使得對任意0＜a＜r,存在臨界點u使得‖u‖=a,Φ(u)=0.

定理1.1的證明 由引理2.1和引理2.2可知Φ(u)∈C1(Hs(Rn))是偶泛函,下有界,滿足PS條件.由定理1的假設f(x,0)=0及(x,u)的定義,有Φ(0)=0.?K＞0,?δ=δ(K)＞0,使得如果則

這表明?k∈N,如果Xk是的k-維子空間,ρk＞0充分小,則有Sρk={u(x)∈Hs(Rn)|‖u(x)‖=ρk},由定理3.1知Φ 有非平凡臨界點列{uk(x)}滿足?k有Φ(uk(x))＜0,當k→ ∞ 時,‖uk(x)‖→0.

最后,來證明當k→∞ 時,有‖uk(x)‖L∞→0,即當k充分大時,uk(x)也是問題(1.1)的解. 記,假設1＜p＜n,當p≥n時,可以類似證明結論成立.若u是(1.1)式的解,α＞0,設M ＞0,記uM(x)=max{?M,min{u(x),M}}.給(2.1)式兩邊同乘以|uM|αuM可以得到

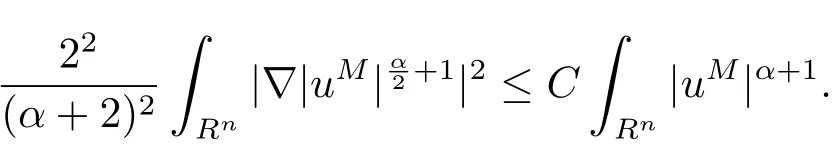
再由分數Sobolev-Hardy不等式[28],則有

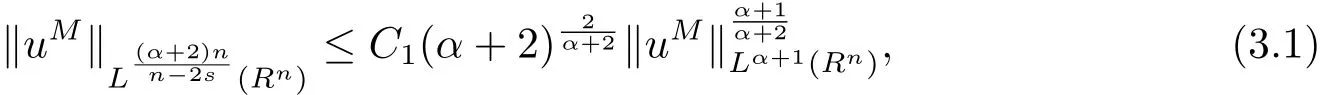
其中 C1＞ 1 是常數,且與 u 和 α 無關.令,即 αk=對 αk重復利用不等式 (3.1) 可得

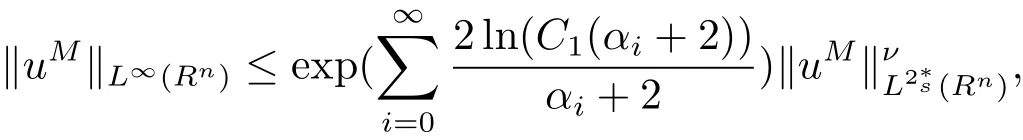
一致成立,則方程組

有無窮多解uk,且當k→∞時,‖uk‖L∞→0,其中??Rn是有光滑邊界的有界域,

u=(u1,u2,···,um)是 m 維向量函數,(?Δ)su=((?Δ)su1,(?Δ)su2,···,(?Δ)sum).

證 考慮方程組

(3.4)式相應的泛函為

則Φ(u)∈ C1(Hs(Rn,Rm)是偶的,強制的,下有界,且滿足PS條件.?k∈N,如果Xk是的k-維子空間,ρk＞ 0充分小,則有Hs(Rn,Rm)|‖u(x)‖= ρ},由定理3.1知Φ 有非平凡臨界點列{uk(x)}滿足對任意k有Φ(uk)＜ 0,當k→ ∞ 時,‖uk(x)‖ → 0.

與定理1.1的證明類似,可以證明當k→∞時,有‖uk(x)‖L∞→0,即對于k充分大時,uk(x)仍然是方程組(3.3)的解.