WEIGHTED INEQUALITIES FOR MAXIMAL OPERATOR IN ORLICZ MARTINGALE CLASSES
CHEN Rui-juan,MENG Fan-yun
(1.Guangling College,Yangzhou University,Yangzhou 225002,China)
(2.School of Mathematical Sciences,Yangzhou University,Yangzhou 225002,China)
Abstract:In this paper,we study weighted inequalities for maximal operators in Orlicz martingale classes.By using the properties of weights,we obtain that inequalities of a(·)and b(·)imply weighted inequalities involving maximal operator in uniformly integral martingale classes.The converse is also considered,which extends the theory of class LlogL.
Keywords: martingale space;maximal operator;weighted inequality;regular condition
1 Introduction
As is well known,for the real-valued local integrable functions f on Rn,the classical Hardy-Littlewood maximal operator M is defined by
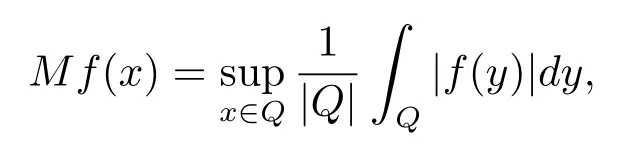
where Q is a non-degenerate cube with its sides paralleled to the coordinate axes and|Q|is the Lebesgue measure of Q.
Suppose that Φ :[0,∞) → R is nondecreasing and continuous with Φ(0)=0 andLet

Then LΦis called an Orlicz space.In Orlicz spaces,Kokilashvili and Krbec[1,Theorem 1.2.1]stated that the following statements are equivalent:
(a)there exists a positive constant C such that
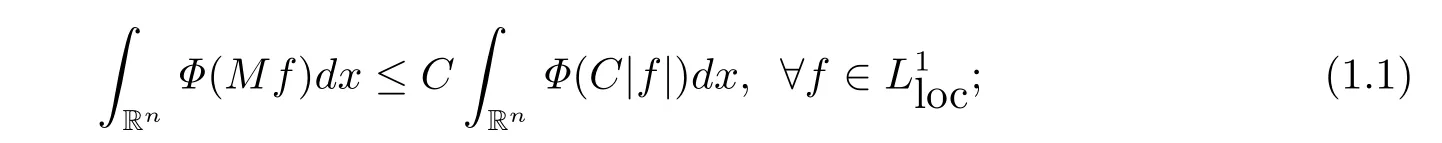
(b)the function Φαis quasi-convex for some α ∈ (0,1).
Let T be the group of real numbers modulo 2π and f(x)a real-valued integrable function denoted on T with period 2π.The Hardy-Littlewood maximal function MTf(x)is defined bywhere the supremum taken over all open I?T with x∈I.
Let a(s)and b(s)be two positive nondecreasing continuous functions defined on[0,∞)satisfying
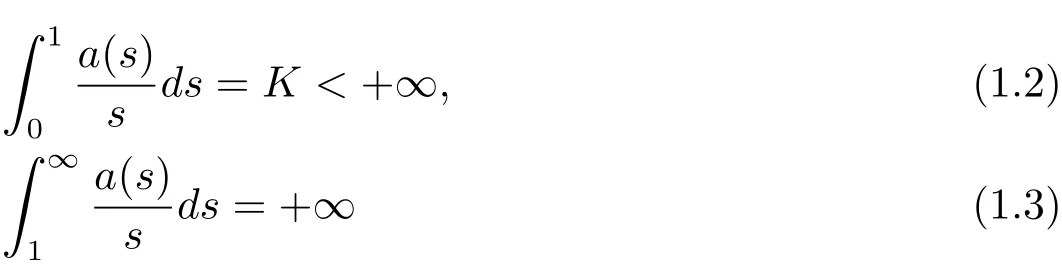
and

Then,we define
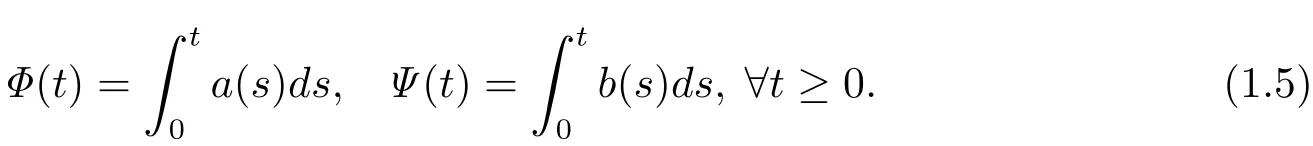
Under hypotheses(1.3)–(1.5),a series of inequalities involving MTf and f were obtained.Kita[3,Theorem 2.1]gave necessary and sufficient conditions for a(·)and b(·)in order to guarantee that MTf is in LΦwhenever f is in LΨ.Conversely,Kita[4,Theorem 2.1]stated necessary and sufficient conditions for a(·)and b(·)in order to guarantee that a function f is in LΨwhenever the function MTf is in LΦ,which is a generalization of[5,Theorem 5.4]to functions in an Orlicz space LΨand also a generalization of the result of[6,Theorem 3.1].These are related to the class of LlogL.The class was introduced by Zygmund to give a sufficient condition on the local integrability of the Hardy-Littlewood maximal operator.The necessity of this condition was observed by Stein[7].
Under the additional hypothesis(1.2),Kita[8,Theorem 2.3,Theorem 2.5]extended the above results[3,Theorem 2.1]and[4,Theorem 2.1]to the cases on Rn.Moreover,Kita[9,10]obtained the related weighted theory on Rn.Specially,Kita[10]also dealt with the iterated maximal operator.
Comparing with the results without weights on Rnand T,Mei and Liu[11,12]considered the martingale cases.In our paper,we prove weighted inequalities for maximal operators in Orlicz martingale classes.Let us introduce some preliminaries.
Let(?,F,μ)be a complete probability space,and(Fn)n≥0be an increasing sequence of sub-F- fields of F with F=WFn.If f=(fn)n≥0is a martingale adapted to(Fn)n≥0,the maximal function(operator)Mf for martingale f=(fn)is defined byIn this paper,the limit of fnis also denoted by f.Specifically,?,(Fn)n≥0,F,νis said to satisfy the R-condition(or simply ν ∈ R),if for all n ≥ 1,Fn∈ Fn,there exists a Gn∈ Fn?1such that Fn? Gnand ν(Gn)≤ d·ν(Fn).In our paper,we assume that F0={?,?}.
A weight ω is a positive random variable with Eω < ∞.For convenience,we assume Eω =1 in this paper.In addition,we say ω ∈ A1(or B1),if ω?1∈ L∞(dμ)and there exists a constant C ≥ 1 such that ωn≤ Cω (or Cωn≥ ω).Moreover,for the weights as above,a function f ∈ L1(ωdμ)implies f ∈ L1(dμ).
Let a(s),b(s),Φ(t)and Ψ(t)satisfy(1.2)–(1.5).It is clear that Φ and Ψ are convex.Recall that LΦ(dμ)∪LΨ(dμ)? L1(dμ)when μ(?)< ∞.
Then we have the following Theorems 1.1 and 1.2,which are martingale versions of[8,Theorem 2.3].Kita[8,Theorem 2.3]gave an assumption that the functionis bounded in a neighborhood of zero.However,we do not need the assumption in our Theorems 1.1 and 1.2.
Theorem 1.1 Let ω∈A1.Suppose that there exists a positive constant C1such that
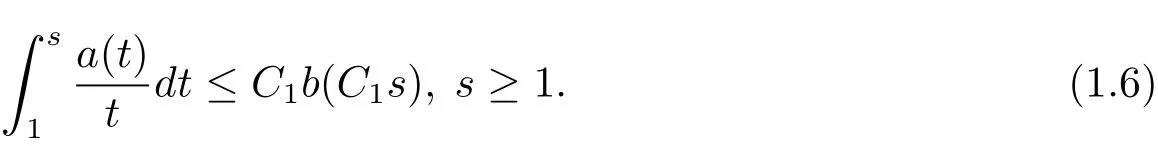
Then there exist positive constants C2and C3such that
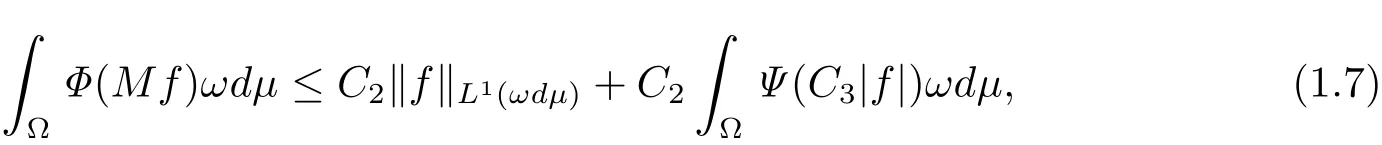
where C2and C3are constants independent of f=(fn).
Theorem 1.2 Let(?,F,ω)be non-atomic and ω ∈ R∩B1.Suppose that f ∈ LΨ(ωdμ)implies Mf ∈ LΦ(ωdμ).Then(1.6)holds.
Following from Theorems 1.1 and 1.2,we easily have Corollaries 1.3 and 1.4,respectively.
Corollary 1.3 Let ω ∈ A1.Suppose that(1.6)is valid,then Mf ∈ LΦ(ωdμ)for all f ∈ LΨ(ωdμ).
Corollary 1.4 Let(?,F,ω)be non-atomic and ω ∈ R∩B1.Suppose that(1.7)is valid,then we have(1.6).
We consider the converse inequality of maximal functions.Theorems 1.5 and 1.6 are martingale versions of[8,Theorem 2.5]and involve weights.
Theorem 1.5 Let ω ∈ B1∩R.Suppose that there exist positive constants C6and s0>1 such that
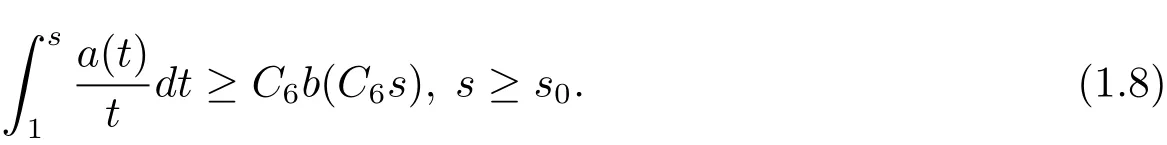
Then there exist positive constants C7and C8such that
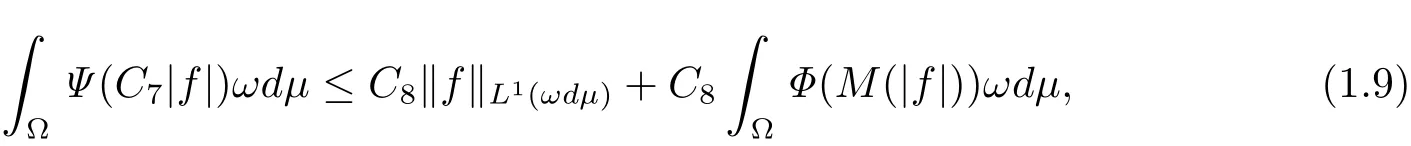
where C7and C8are constants independent of f=(fn)and ‖f‖L1(ωdμ)≤ 1.
Theorem 1.6 Let(?,F,ω)be non-atomic and ω ∈ A1.Suppose that(1.9)is valid.Then(1.8)holds.
We easily obtain Corollary 1.7 by Theorems 1.5.In addition,following the proof of Theorem 1.6,we have Corollary 1.8.
Corollary 1.7 Let ω ∈ B1∩R.Suppose that(1.8)is valid.Then f ∈ LΨ(ωdμ)for all f satisfying Mf ∈ LΦ(ωdμ).
Corollary 1.8 Let(?,F,ω)be non-atomic and ω ∈ A1.Suppose that Mf ∈ LΦ(ωdμ)implies f ∈ LΨ(ωdμ).Then(1.8)holds.
2 Proofs of Theorems
First,we give some lemmas which will be used in our proofs several times.
Lemma 2.1 Suppose that ν is an finite measure on(?,F),then for each function f ∈ L1(dν),we have
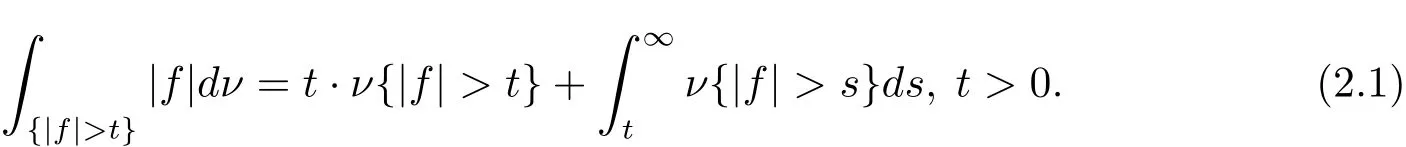
Proof The proof follows in the same way as the proof of[9,Lemma 3.1].
Lemma 2.2 Let ω∈A1.Then there exists a positive constant C0such that
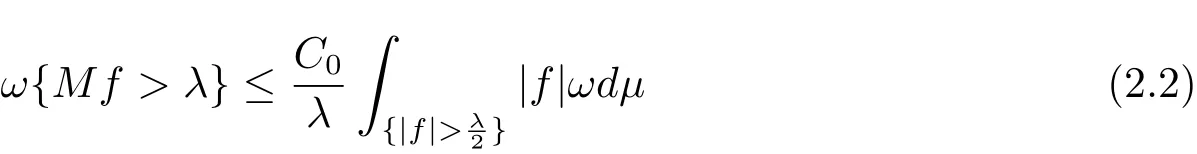
for all λ > 0 and f ∈ L1(ωdμ).
Proof By the assumption that ω∈A1,there exists a positive constant C such that
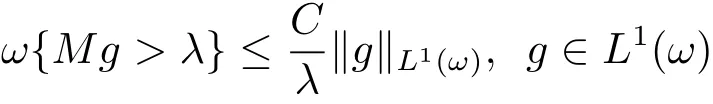
in view of[13,Theorem 6.6.2].For λ > 0,we setand fλ=f?fλ.Then fλ∈ L1(ω)andIt follows that
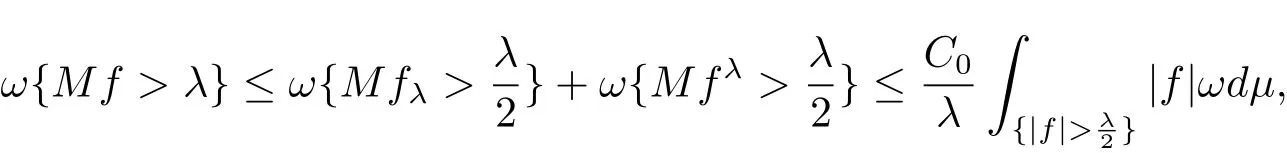
where C0=2C.
Lemma 2.3 Let ω∈A1.Then there exists a positive constant C such that
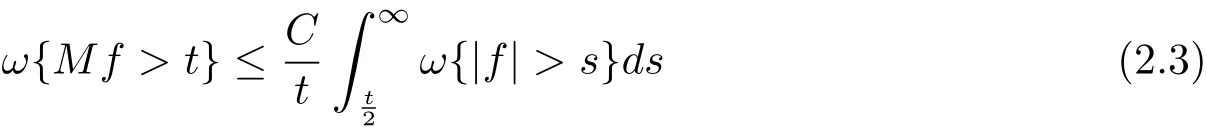
for all t> 0 and f ∈ LΨ(ω).
Proof Fix f ∈ LΨ(ωdμ).For t> 0,set ft=(|f|∧)·signf and ft=f ?ft.Trivially,we have ft∈ L1(ω).By Lemma 2.2,we also have
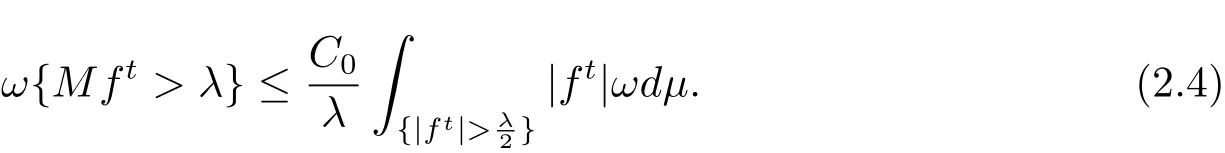
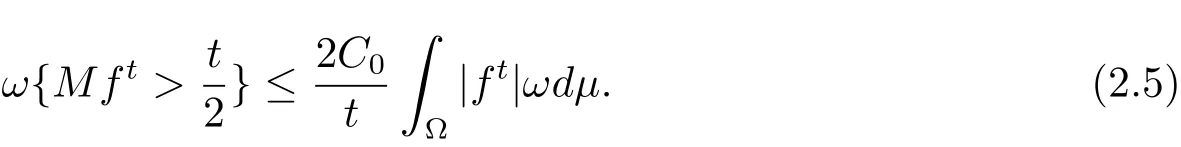
Hence,
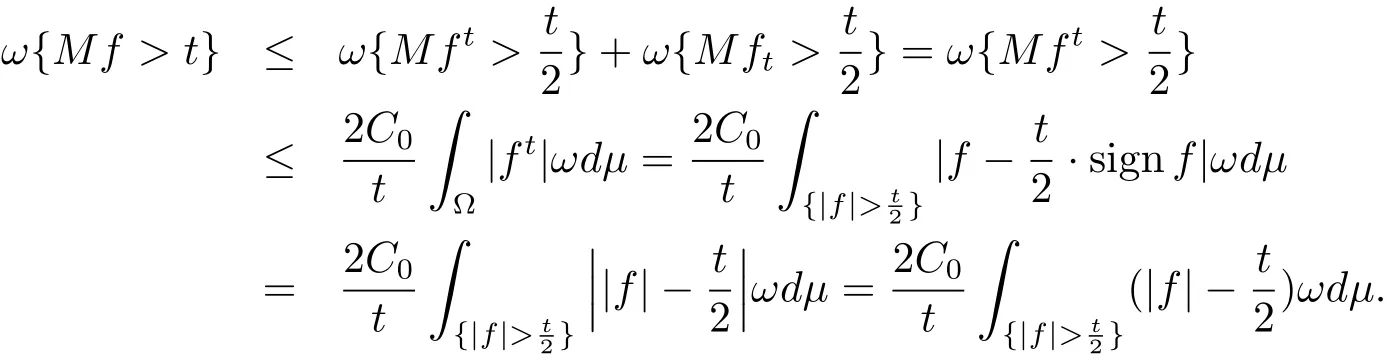
Combining with(2.1),we have(2.3)is valid with C=2C0.
Proof of Theorem 1.1 For C3> 0(which will be determined later), fix f ∈ LΨ(ωdμ)such thatWith the constant C in Lemma 2.3,it follows from(1.2),(1.3)and(1.6)that
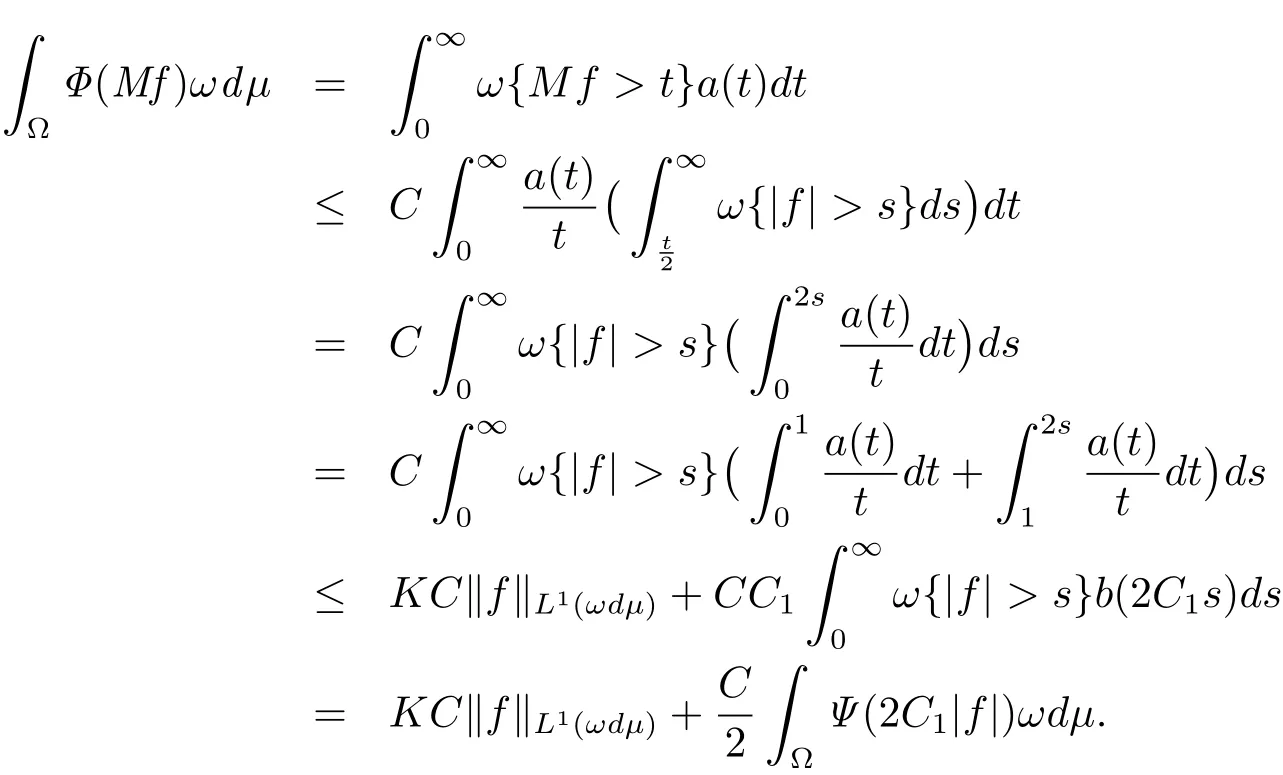
Let C2=(KC)∨and C3=2C1.The we have(1.7).
In order to give the proof of Theorem 1.2,we need the following lemmas.
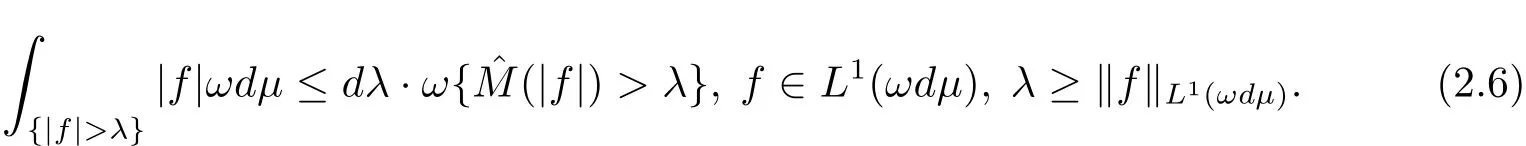
ProofFor f∈L1(ωdμ),the sequenceis a uniformly integral martingale with respect to(?,(Fn)n≥0,F,ωdμ).In view of[13,Theorem 1.3.2.9],we havea.e..Then it follows that
Because of ω∈R,we have
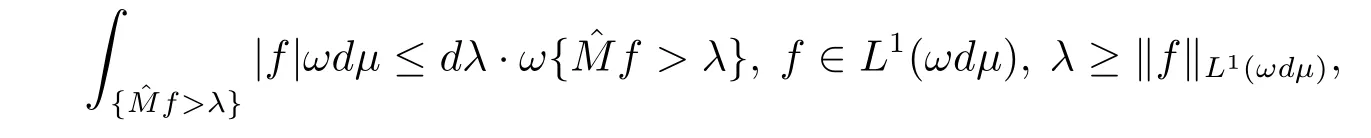
where we use[13,Theorem 7.1.2].Combining this withwe have

Lemma 2.5 Let ω be a weight.Then
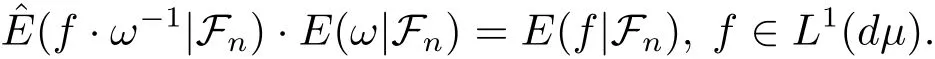
Proof For all A∈Fn,we have
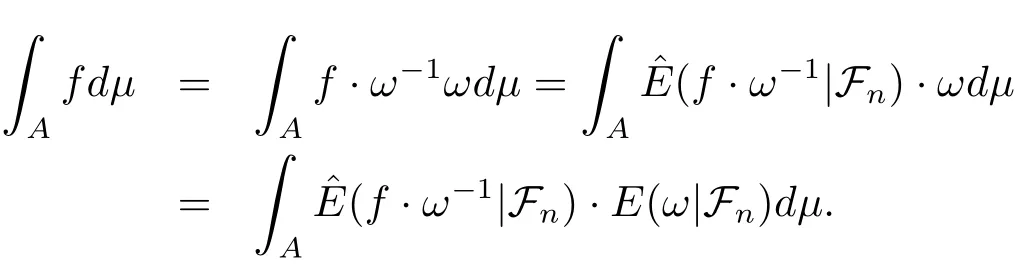
Reforming Lemma 2.5,we have

Lemma 2.6 Suppose ω ∈ B1∩R.Then there exist constants C4and C5such that
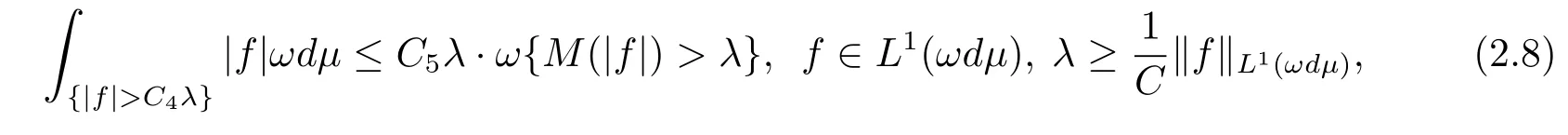
where the constant C is the one in the definition of B1.
Proof Fix f ∈ L1(ωdμ)andSince ω ∈ B1,there exists a constant C ≥1 such that C ·ωn≥ ω.Combining this with(2.7),we have
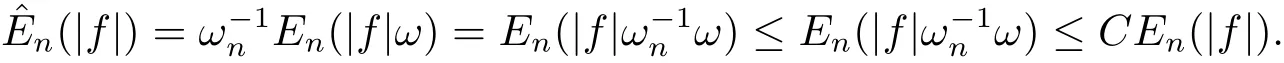
Thus

Since Cλ ≥ ‖f‖L1(ωdμ),we have
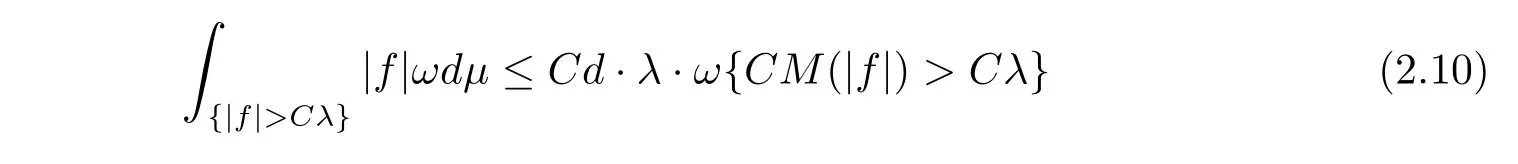
in view of Lemma 2.4.Thus,(2.8)is valid with C4=C and C5=Cd.
Proof of Theorem 1.2 Assume for contradiction that(1.6)does not hold.Then there exists a sequence of positive numbers sk≥1 such that
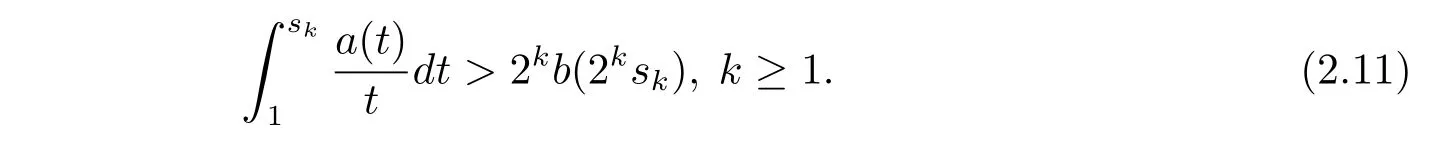

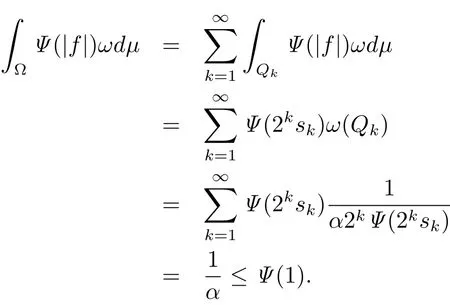
Thus f ∈ LΨ(ωdμ).By Jensen’s inequality,we have f ∈ L1(ωdμ)and ‖f‖L1(ωdμ)≤ 1.
On the other side,we claim that the function Mf is not in LΦ(ωdμ).Then we get a contradiction.To show the claim in the following way: fix a constant ε∈ (0,1]for εf,with C,C4and C5in Lemma 2.6,we have
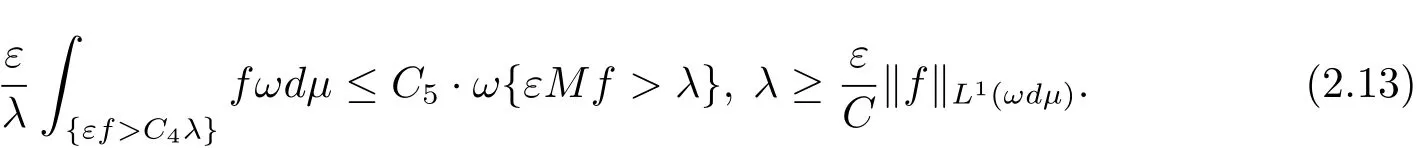
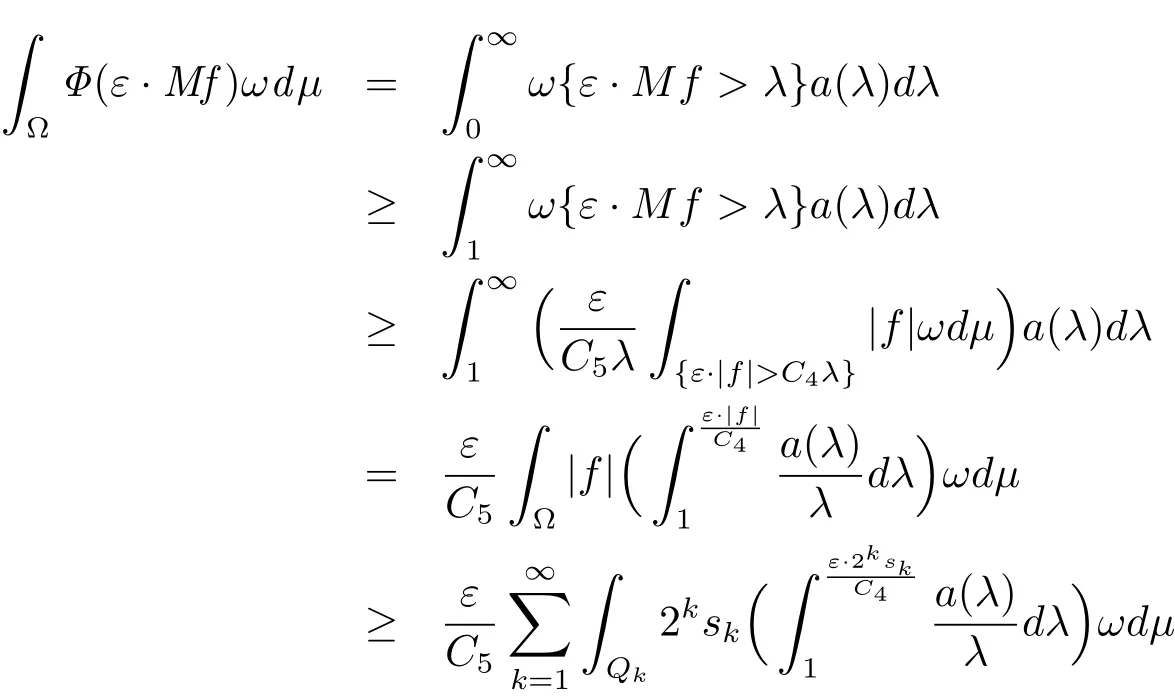
For the above ε,we can choose k(ε)such that,k ≥ k(ε).Put
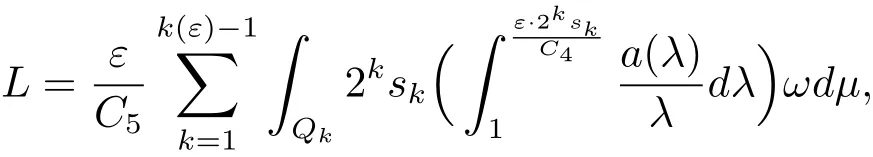
then L is a real number.Therefore,it follows from(2.11)and(2.12)that
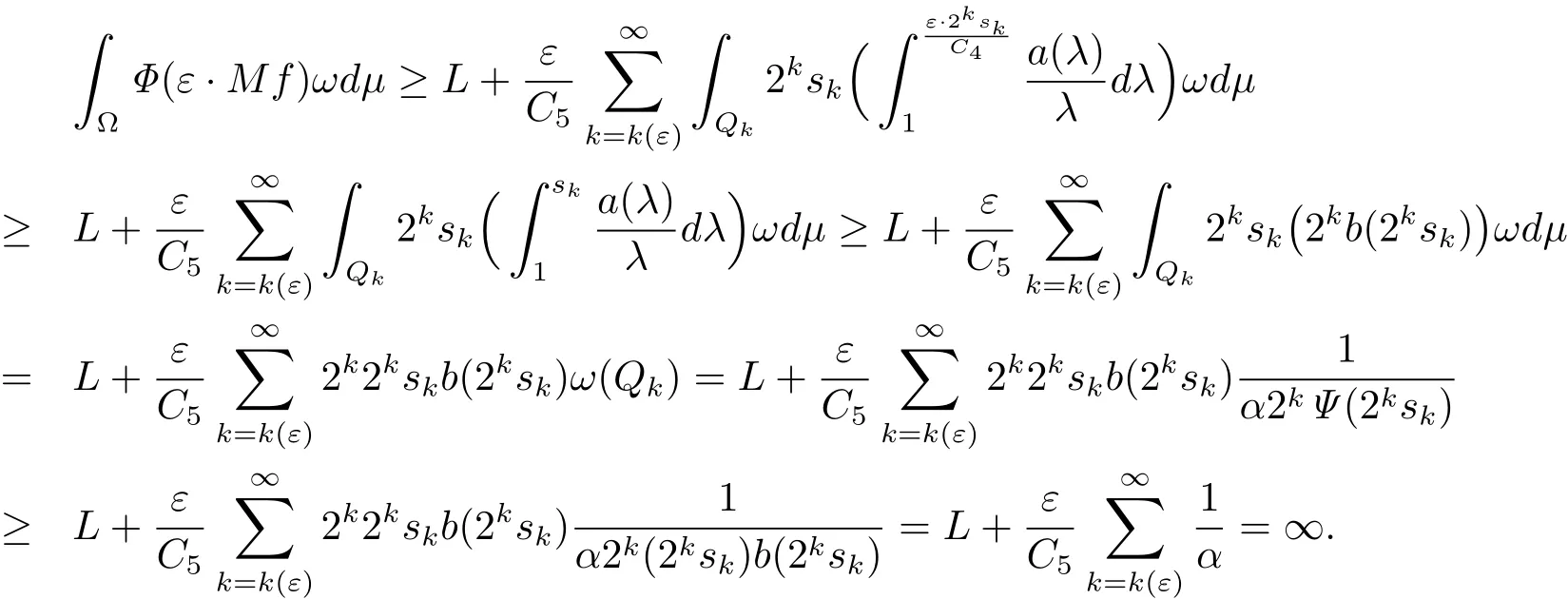
The claim is proved and the proof is finished.
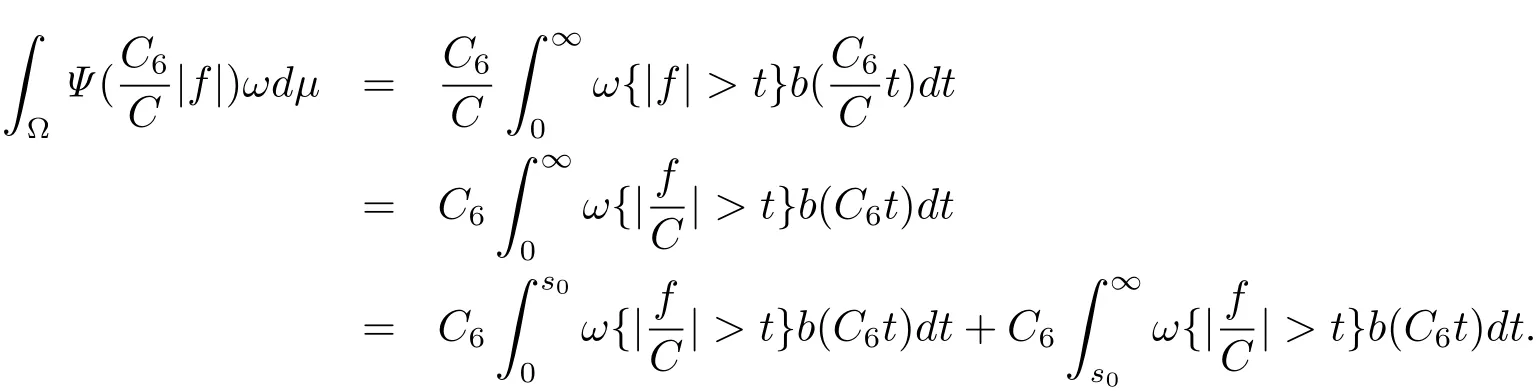
Denote
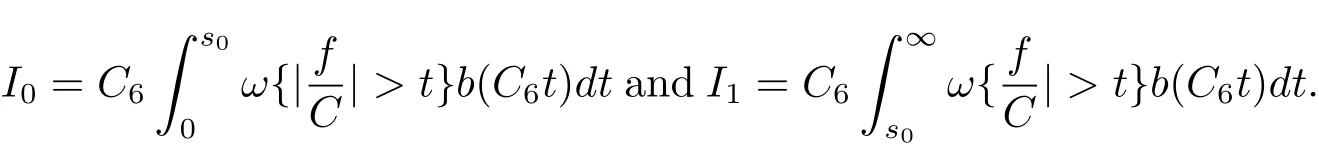
Then,for I0,we have
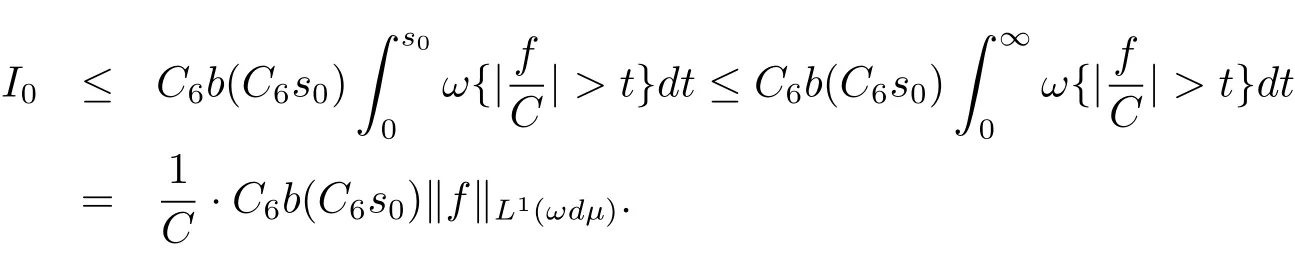
It follows from(1.8)that
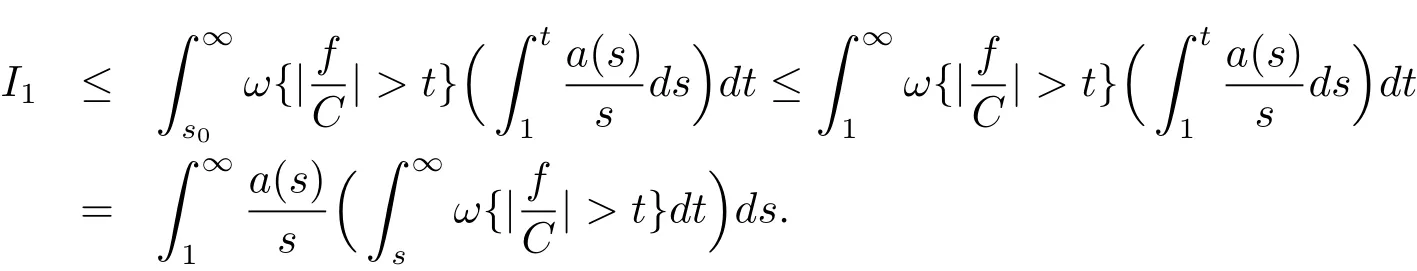
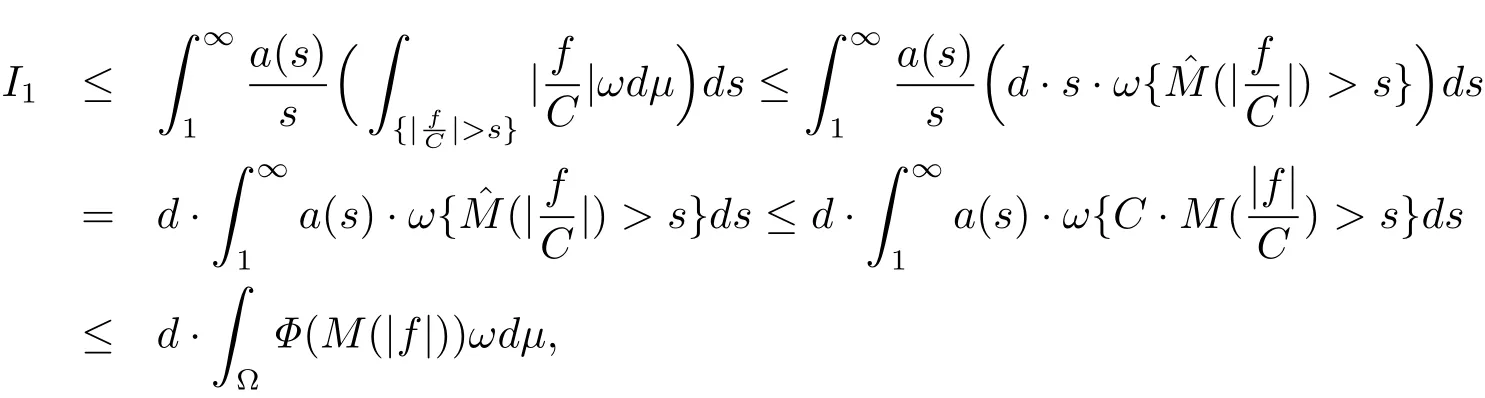
It follows from(2.1),(2.6)and(2.9)that where we have used.Therefore,(1.9)is valid withand
Proof of Theorem 1.6 We proceed by contradiction and assume that(1.8)dose not hold.Then we get a sequence sk>1 satisfying
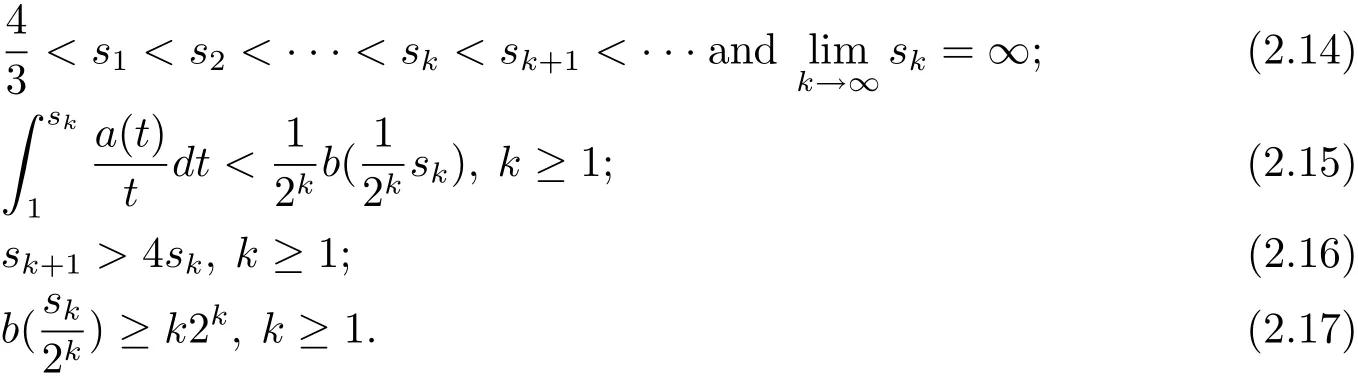
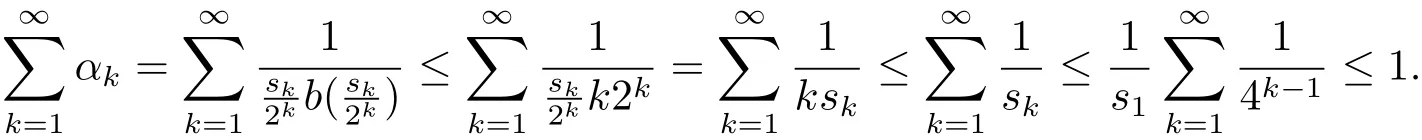
By the assumption that(?,F,ω)is non-atomic,we have a family of measurable sets Qk∈ F such that
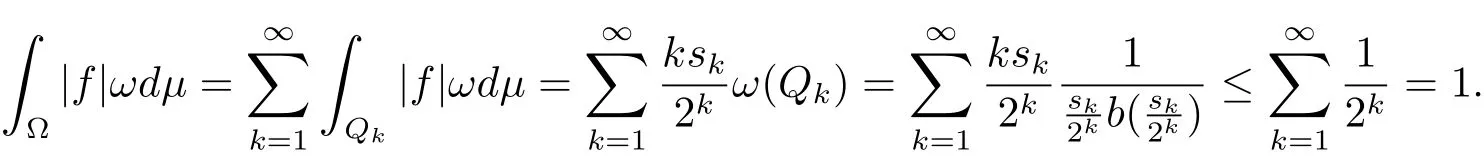
Thus f ∈ L1(ωdμ)and ‖f‖L1(ωdμ)≤ 1.Moreover,we also have.In fact,for the sequence sk,we have
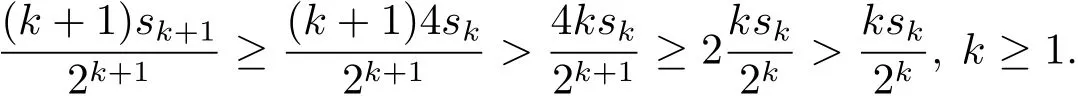
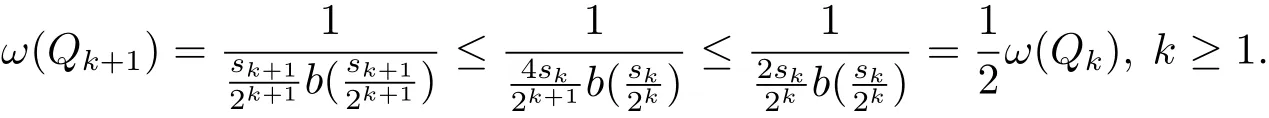
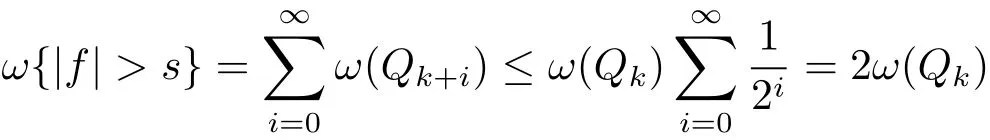
and
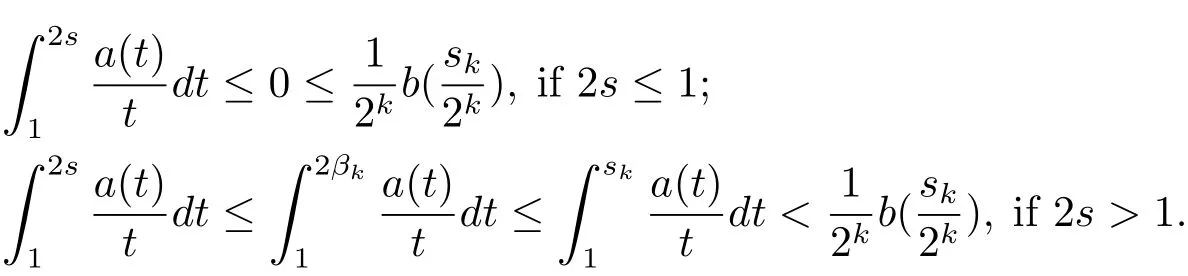
Combining(2.3),(1.2)and(1.3),we have
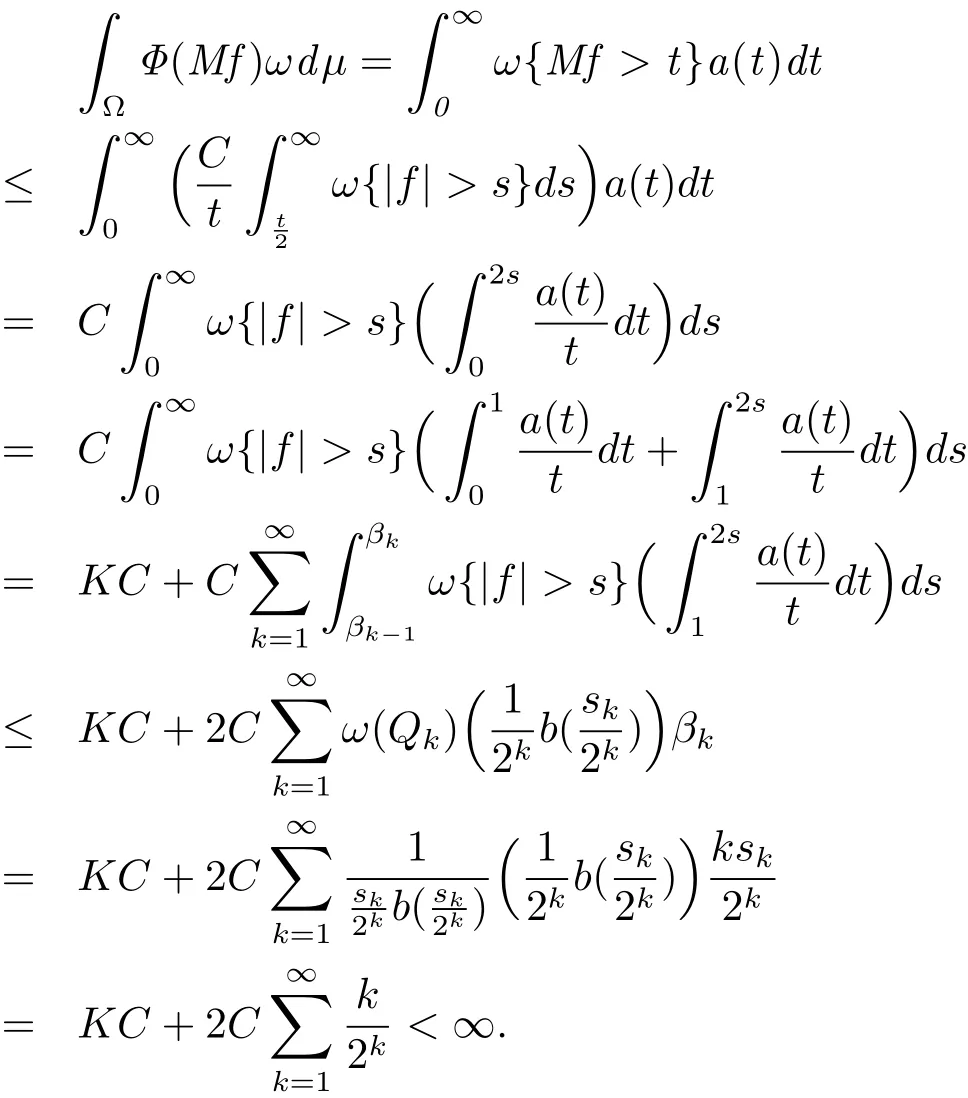
On the other hand,we have
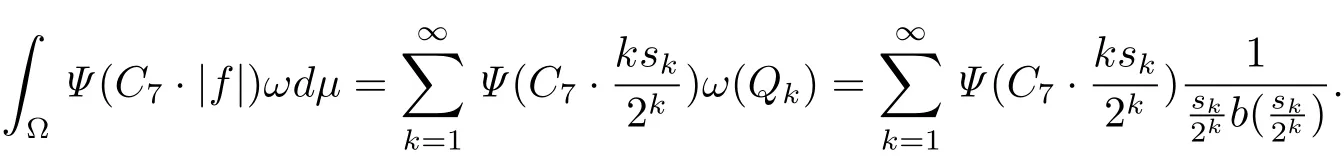
For the above C7,we can choose a constant k(C7)> 0 such that k·C7≥ 2,k> k(C7).Therefore,
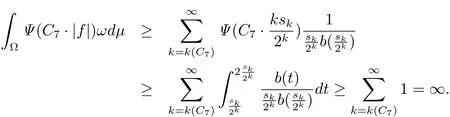
The result contradicts assumption(1.9).This completes the proof.

