非平穩色噪聲背景下非相關與相干信源數估計算法
陳明建,黃中瑞,龍國慶,韓 旭
(國防科技大學電子對抗學院,合肥 安徽 230037)
0 引言
信源數估計是陣列信號處理的重要內容[1]。典型的信源數估計方法包括基于AIC準則[2]和MDL準則[3-4]的信息論方法。該方法假設噪聲為理想高斯白噪聲,而實際的噪聲模型可能是空間非平穩色噪聲,此時該算法性能下降甚至失效。為了解決該問題,近些年來針對色噪聲背景下的信源數估計方法相繼提出,如蓋氏圓盤法(GDE)[5]、K均值法[6]、修正的MDL算法[7]、基于對角加載的特征值校正方法[8]、SORTE法[9]以及基于重采樣的Bootstrap法[10]等。但上述算法均假定信源是不相關或者獨立的,若空間信源存在一定的相關性或者完全相干時,此時數據協方差矩陣將會出現缺秩,導致算法性能下降甚至失效。
為了解決相干信源數估計問題,學者們提出了很多算法,一般可分為兩大類:一類是空間平滑類算法,主要包括前向空間平滑算法[11-12]、前后向空間平滑算法[13-14]以及空間差分平滑算法[15-16]。空間平滑算法是以犧牲有效的陣元來恢復相干信號協方差矩陣的秩,而且無法區分相干和非相干源數目,因此估計最大信源數不超過陣元數目。空間差分平滑算法將陣列協方差矩陣分為Toeplize部分和非Toeplize部分,利用差分運算得只含相干信源的協方差矩陣,提高了算法對信源的過載能力,但文中沒有討論非相關信源數估計問題。另一類是矩陣重構法,包括Toeplize矩陣重構算法[17]、ESPRIT-Like算法等[18],均是利用矩陣重構方式解相干。但該類方法需要犧牲一半的陣元恢復數據協方差矩陣的秩,估計信源數有限。針對空間非平穩色噪聲背景下,傳統信源數估計算法性能下降,且估計信源數有限的問題,本文提出了非平穩色噪聲背景下非相關與相干信源數估計算法,并通過仿真實驗驗證了該算法的有效性。
全文中,符號(?)T、(?)*、(?)H和E{?}分別表示轉置、共軛、共軛轉置和求統計期望,diag{α1,α2,…,αk}代表由對角元素α1,α2,…,αk組成的對角矩陣,blkdiag{Z1,Z2}表示由矩陣Z1,Z2組成的塊對角矩陣,
1 信號模型
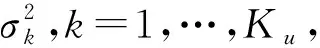
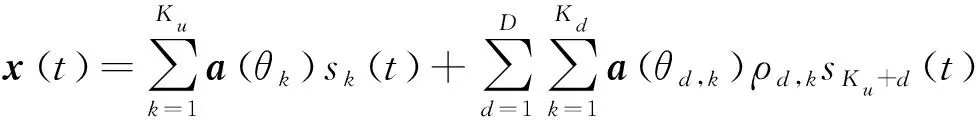
(1)
其中,a(θ)是均勻線陣陣列導向矢量,可表示為:
a(θ)=[1,μ1,,…,μM-1]T,μ=ejπsin(θ)
(2)
A=[Au,AcΓ]∈M×K為所有信源導向矢量矩陣,Au=[a(θ1),…,a(θKu)]為非相關信源導向矢量矩陣,Ac=[Ac,1,…,Ac,D]為相干信源導向矢量矩陣,Ac,d=[a(θd,Kd),…,a(θd,Kd)],Γ=blkdiag{ρ1,…,ρD},ρd=[ρd,1,…,ρd,Kd]T,其中ρd,k表示第d組的第k個相干信號相對于該組第1個信號的衰落系數,相干信號來波方向為M×1維復圓零均值高斯噪聲,且與信號不相關,則x(t)的協方差矩陣表示為:
(3)
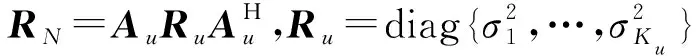
(4)
2 信源數估計算法
2.1 非相關信源數估計
假定M-1≥Ku+D,若對矩陣R特征分解可得
(5)
式(5)中Us=[u1,…,uKu+D]、Σs=diag{λ1,…,
λKu+D};Un=[uKu+D+1,…,uM],Σn=diag{λKu+D+1,
…,λM};λ1≥λ2…≥λKu+D≥λKu+D+1≥…≥λM。
記M個數據點為(1,λ1),(2,λ2),…,(M,λM),期望通過這M個數據點擬合一條直線。假定直線方程為:
y=ax+b
(6)
則點(xi,yi)到直線的距離為:
(7)
所有觀測值到直線的距離平方和可表示為:
(8)
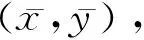

(9)

對于總體最小二乘的特征值擬合誤差可表示為:
(10)
式(10)中,ε(k)表示參與擬合的第M-k+1到第M個點到擬合直線的距離平方和。
由線性擬合可知ε(k)為單調遞減函數,且ε(1),…,ε(M-Ku-D)兩兩之間的差別要小于ε(M-Ku-D+1),…,ε(M-1)兩兩之間的差別。因此可以根據ε(k)的梯度信息估計信源數,即

(11)
當k從小到大時,假定TLS(k)第一次出現負數時為k0,則信源數為k0-1,即為非相關信源個數與相干信號組數之和估計值。
|aH(θ)Un|2=0,θ=θi,i=1,…,Ku
(12)
|(Aiρi)HUn|2=0,i=1,…,D
(13)
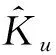
2.2 相關信源數估計
假定將均勻線陣劃分為相互重疊的p個子陣,其中每個子陣包含有相同的陣元數M-p+1。則第k個子陣的陣列數據協方差矩陣為:
(14)
式(14)中,Fk=[0(M-p+1)×(k-1)IM-p+10(M-p+1)×(p-k)]。
定義:對于M×M維矩陣R,空間差分平滑矩陣為:
(15)
式(15)中,矩陣JM為m×m階置換矩陣。
命題1:若非相關信源和相干信源同時入射ULA陣列,則Rsd不含有非相關信源信息。
證明:為了簡化分析,只需考慮R中的非相關信源RN部分。即等價證明
(16)
(17)
式(17)中,Ω=diag{ejπsin(θ1),…,ejπsin(θKu)}。
由于均勻線陣的導向矢量矩陣A(θ)為范德蒙德矩陣,因此可得
(18)

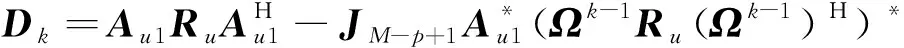
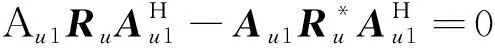
(19)
由式(19)可知,Dk中不含有非相關信源信息,因此命題1成立。證畢。
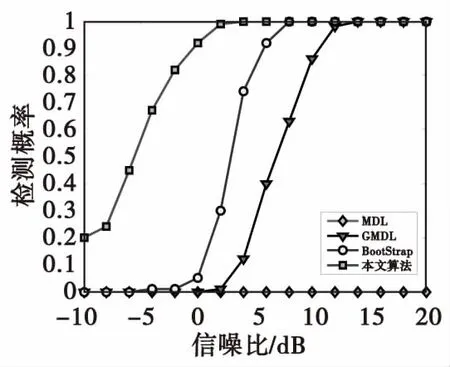
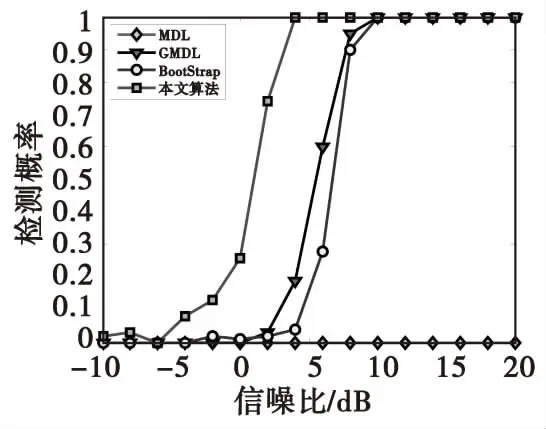
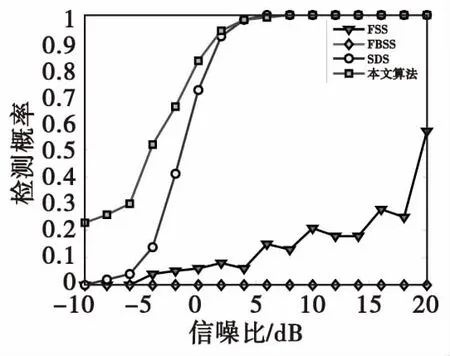
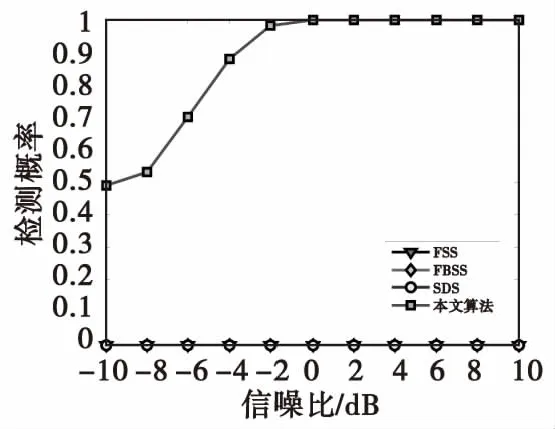
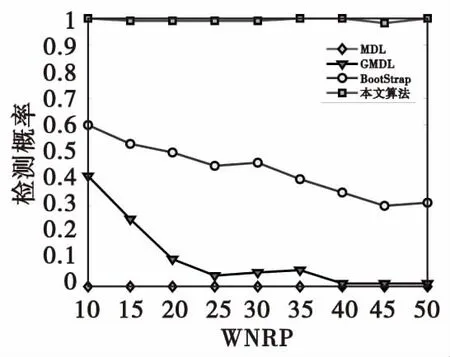
命題2:若均勻線陣入射信源含有非相關信源和相干信源,其中有D組共Kc個相干信源,第d(d=1,2…,D)組相干信源包含了Pd個多徑信號,若將M元均勻線陣劃分為相互重疊的p個子陣,子陣陣元數為M-p+1,若p≥max{K1,…,KD}?Kmax,且Kc 證明:命題1已證明Rsd不含有非相關信源信息,因此Rsd可以等價表示為: (20) 其中, (21) 式(21)中,Ac1=F1Ac,B=blkdiag{γ1,…,γD},γd=diag{ejπsin(θd,1),…,ejπsin(θd,Kd)}。 將式(21)代入到式(20)中可得 (22) (23) (24) (25) (26) 式(26)中, (27) (28) 當p≥max{K1,…,KD}=Kmax,式(25)可表示為: (29) 式(29)表明當p≥Kmax,M-p+1>Kc時,Rsd恢復為滿秩矩陣,即rank(Rsd)=Kc。證畢。 由命題1、命題2可知,若p滿足Kmax≤p≤M-Kc+1,則Rsd只含有相干信源信息且是滿秩矩陣。對Rsd特征分解可得 (30) 同理,利用特征值的線性擬合誤差可實現相干信源數估計。 綜上所述,本文算法基本步驟可歸納如下: 3) 利用式(15)計算空間差分平滑矩陣Rsd; 假定有K個窄帶信號以平面波入射ULA,其中非相關信源數為Ku,D組相干信源總數為Kc。若要成功分辨所有入射信號,對于前向平滑FSS法、前后向平滑FBSS法、空間差分平滑SDS法需要陣元數至少分別為Ku+Kc+3Pmax/2、Ku+Kc+Pmax/2、max{(Ku+D+1),Pmax/2+Kc+1},本文算法最少需要陣元數為max{(Ku+D+1),Kc+2}。 由上述分析可知FBSS算法由于采用了前后平滑處理,其陣列需求小于FSS算法,本文算法所需陣元數最少,SDS算法性能次之。 本節仿真實驗分為兩部分。第一部分考察空間非平穩色噪聲對非相關信源數估計的影響,主要對比常規MDL算法、文獻[7]的GMDL算法、文獻[10]Bootstrap算法以及本文算法的性能;第二部分驗證一種新的空間差分平滑算法對相干信源數估計有效性,主要對比分析常規的FSS算法、FBSS算法、文獻[16]SDS法以及本文算法。 實驗1信源數檢測概率與SNR關系 考慮陣元數M=10,3個非相關信號和2組4個相干窄帶信號同時入射到陣列上,非相關信號DOA分別為[-2° -13° 42°],相干信號DOA分別為[-14° -5°],[29° 65°],噪聲的協方差矩陣Q=diag{3.3,2.6,5.2,1.2,4.1,5.0,3.2,6.0,3.0,3.5}。圖1、圖2分別是非相關信源數、所有信源數的檢測概率與SNR關系曲線。 圖1 相關信源數檢測概率與SNR關系Fig.1 Probability of correct detection for uncorrelated sources versus 由圖1可知,在空間非平穩色噪聲條件下MDL算法將失效,其他三類算法均能實現信源數有效估計,GMDL算法對MDL算法的似然函數和罰函數均進行了修正,因此提高了算法的性能;Bootstrap算法采用了重采樣技術,并結合GDE算法的思想,可以避免對數據分布做出假設,并適用于色噪聲模型。本文算法采用特征值總體最小二乘線性擬合,并利用擬合誤差的梯度信息,實現了空間非平穩色噪聲背景下的信源數估計,本文算法性能要優于其他三類算法,Bootstrap算法次之,GMDL性能介于本文算法與GMDL之間。 圖2 所有信源數檢測概率與SNR關系Fig.2 Probability of correct detection for uncorrelated and coherent sources versus input SNR 圖2是針對非相關和相干信源共存時四類算法信源數估計性能。從圖2可知,FBSS算法性能優于FSS算法。在低信噪比時SDS算法空間差分平滑技術能消除部分噪聲,相當于提高了SNR,因此性能優于傳統的空間平滑算法,但在信噪比大于5 dB時,FBSS性能要優于SDS;而本文算法性能在任意信噪比條件下性能均優于其他三類算法。 實驗2角度相近時信源數檢測概率與SNR關系 考慮3個非相關信號和2組4個相干窄帶信同時入射到陣列上,非相關信號DOA分別為[-2° -13° 42°],相干信號DOA分別為[-14° -3°],[29° 43°]。圖3、圖4分別是非相關信源數、所有信源數的檢測概率與SNR關系。 圖3 角度相近時非相關信源數檢測概率與SNR關系Fig.3 Probability of correct detection for closely spaced and uncorrelated sources versus input SNR 由圖3可知,由于非相關信源的來波方向均與相干信源來波方向相近,此時導向矢量矩陣列向量存在相關性,該相關性會影響數據協方差矩陣的特征值分布,Bootstrap算法與本文算法均是利用特征值信息實現信源數估計,因此算法性能均有一定程度下降。而GMDL算法是利用蓋世圓半徑求解信源數,因此導向矢量的相關性對其性能影響較小。 圖4 角度相近時所有信源數檢測概率與SNR關系Fig.4 Probability of correct detection for closely spaced all sources versus input SNR 由圖4可知:傳統FSS、FBSS算法通過空間平滑后數據協方差矩陣仍然可能是缺秩,因此無法正確分辨角度相近的信源,而本文算法和SDS通過空間差分平滑,將非相關信源與相干信源分開檢測,因此信源數檢測性能不受角度間隔的影響。 實驗3信源數超過陣元數時檢測概率與SNR關系 假定M=8,陣列噪聲協方差矩陣Q=diag{10.0 2.0 1.5 2.5 5.0 1.0 1.5 3.0}。共有10個遠場窄帶信號,其中4個非相關信號DOA分別為[-40° -20° -10° 0°],2組6個相干信號DOA分別為[-30° -10° 5°],[20° 40° 60°],其他仿真參數同實驗3。圖5是信源數超過陣元數時檢測概率與SNR關系。 圖5 信源數超過陣元數時檢測概率與SNR關系Fig.5 Probability of correct detection versus input SNR when the number of signals is more than the number of array element 當Ku=4,Kc=6,D=2,Pmax=3時FSS、FBSS、SDS以及本文算法最少需要的陣元數分別為12,9,8,9。因此理論上FSS、FBSS、SDS算法均失效,只有本文算法能夠有效檢測10個入射信號,圖5的仿真結果與理論分析相一致。 實驗4空間非平穩色噪聲背景下算法檢測概率與WNPR關系 由圖6可知,MDL算法基本失效, GMDL算法、Bootstrap算法的檢測概率均隨著WNPR增大逐漸降低。只有本文算法對WNPR變化不敏感,即使在低SNR、高WNPR檢測概率接近1,因此本文方法對空間非平穩色噪聲具有一定的穩健性。 圖6 SNR為0 dB檢測概率與WNPR關系Fig.6 Probability of correct detection versus WNPR for SNR=0 dB 本文提出了非平穩色噪聲背景下非相關與相干信源數估計算法,該算法利用協方差矩陣特征值的總體最小二乘線性擬合,實現了非相關信源估計;然后通過空間差分平滑技術,剔除非相關信源和非平穩空間色噪聲的影響;最后利用線性擬合算法實現相干信源數估計。仿真結果表明,該算法在空間非平穩色噪聲背景下能實現非相關與相干信源數的有效估計,檢測信源數可以超過陣元數,尤其對于角度相近的信源,估計性能要優于其他類信源數估計算法。
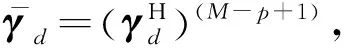
2.3 最少陣元需求分析
3 仿真實驗

4 結論

