基于攻角修正系數的落點預測方法

楊小會，王 超，薛 冰

(機電動態控制重點實驗室，陜西 西安 710065)

0 引言

彈道修正引信是集成有傳統引信功能和彈道修正功能的新型引信[1]，能顯著提高中大口徑系列榴彈的打擊效能和效費比[2]，是大量庫存彈藥精確打擊改造的重要途徑。落點預測是彈道修正技術的關鍵技術之一，其精度和實時性直接影響彈道修正的效果[3]。采用衛星定位進行彈道測量，利用當前彈道參數結合理想的彈道模型外推實際落點是一種常用的方法[4]。

落點預測通常采用的彈道模型有六自由度模型、四自由度模型及質點模型三種。六自由度彈道模型精度高，但是需要測量彈道參數和彈丸姿態參數，模型復雜，計算量大，對硬件要求較高[5]。三自由度的質點彈道模型簡單，計算量少，但其僅在射程較小或彈道末段效果好[6]。四自由度彈道模型僅需要測量彈道參數，計算量少[7]，但由于其無需測量彈丸姿態，攻角僅用角運動方程的解析解直接算出，加之彈道修正過程中攻角變化劇烈，因此解算精度不高，影響落點預測精度。針對四自由度模型中攻角解算精度不高引起落點預測精度低的問題，本文提出了基于攻角修正系數的落點預測方法。

1 攻角對落點預測精度的影響

以155 mm底凹彈為平臺，初速930 m/s，射角51°，采用雙旋彈道模型和四自由度彈道模型解算彈道，兩種模型解算的彈丸攻角隨時間變化見圖1，同一時刻攻角的比值即攻角修正系數見圖2。

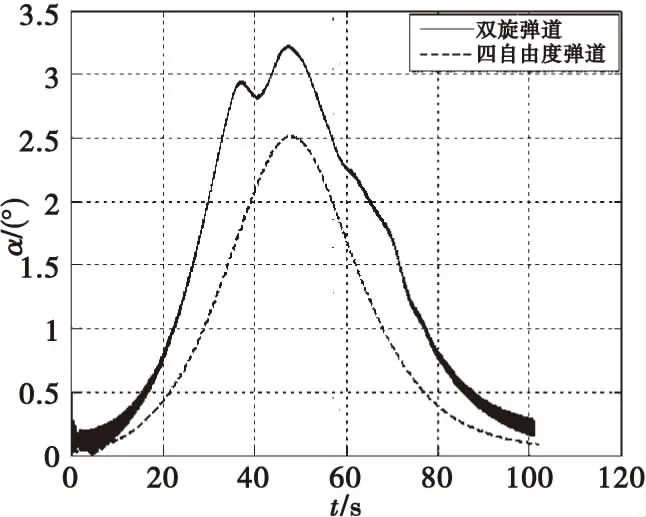
圖1 彈丸攻角Fig.1 Attack angle of projectile

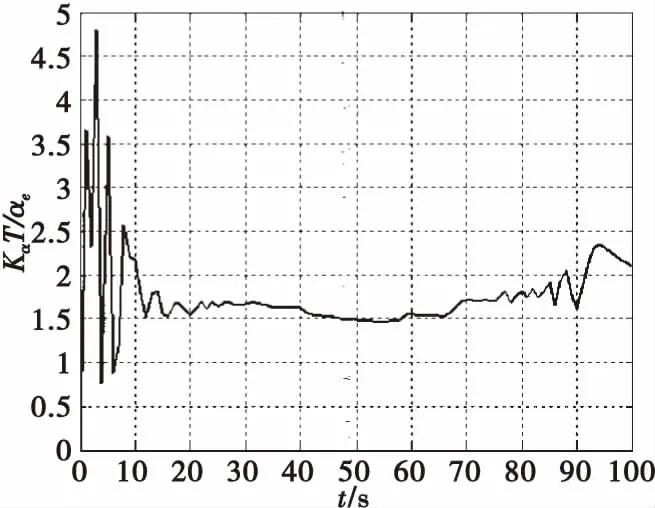
圖2 攻角修正系數Fig.2 Modified coefficient of attack angle

由圖1可以看出，四自由度彈道模型和雙旋彈道模型解算的攻角相差較大，會導致攻角誘導阻力和馬格努斯力與真值相差較大，進而影響射距和橫偏的預測精度。

在不引入任何誤差的條件下，不同預測時刻四自由度彈道模型落點預測誤差見圖3。采用圖2的攻角修正系數修正四自由度彈道模型攻角進行預測落點，預測誤差見圖4。通過圖3和圖4誤差對比可見，采用修正系數修正攻角同時降低了射距誤差和橫偏誤差，60 s后落點預測誤差絕對值小于20 m，提高了落點預測的精度。

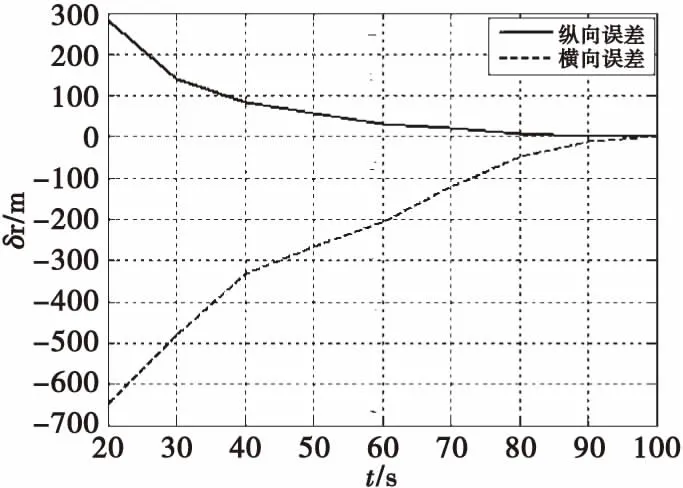
圖3 四自由度彈道模型落點預測誤差Fig.3 IPP error without modified attack angle

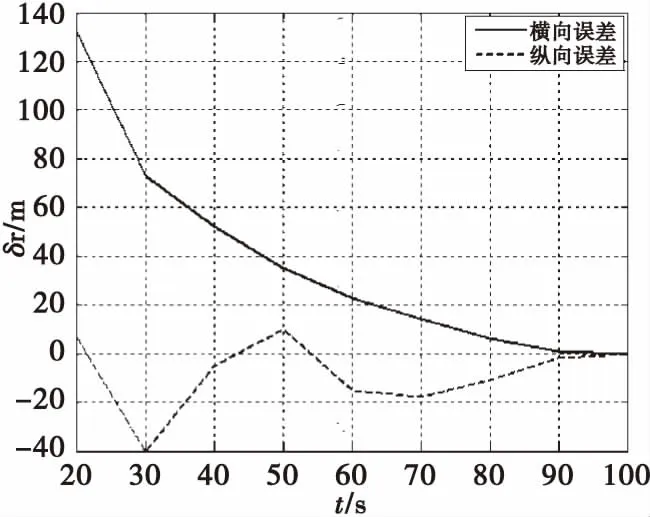
圖4 采用修正后攻角不同時刻落點預測誤差Fig.4 IPP error with modified attack angle

2 基于攻角修正系數的落點預測方法

2.1 攻角修正系數獲取方法

四自由度彈道模型落點預測誤差不單是攻角解算誤差，還包含彈道氣象散布、彈丸偏心、彈丸的質量及氣動散布等因素引起的誤差。這些誤差都會影響攻角的計算精度，表現為攻角修正系數值產生波動，可通過卡爾曼濾波獲取攻角修正系數的最優估值，進而減弱這些誤差對落點預測精度的影響。

濾波的狀態方程選擇為四自由度彈道模型，其為多變量非線性方程，需采用非線性濾波。非線性濾波器中常用的是擴展卡爾曼濾波器，其首先利用泰勒級數將非線性方程展開，通過一階線性方程近似原有非線性方程，根據彈道測量模塊的觀測值，獲取彈道參數及攻角修正系數的最優估計值。

2.1.1狀態變量及狀態方程

濾波的狀態變量選擇為位置、速度、轉速及攻角修正系數8個，對應的狀態方程采用引入攻角修正系數的四自由度彈道模型，由圖2可知，攻角修正系數近似為常值，因此攻角修正系數的模型選為常值函數，如式(1)所示。

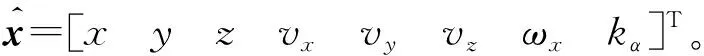
狀態方程：

(1)

cx0、cxα2分別表示零升阻力系數和誘導阻力系數，cy、cz和clp分別表示升力系數導數、馬格努斯力系數導數和極阻尼力矩系數導數；m、d、s和Jx分別表示彈丸質量、彈徑、彈丸參考面積和極轉動慣量；ρ表示空氣密度；Q表示模型噪聲。

αe表示攻角，計算公式見式(2)。

(2)

2.1.2量測變量及量測方程

濾波的量變量選擇為衛星定位測量的發射系位置、速度信息，磁傳感器測量的轉速信息共7個，對應的量測方程如公式(3)所示。

(3)

式(3)中，R表示量測噪聲，量測轉移矩陣

2.2 基于攻角修正系數的落點預測方法

采用擴展卡爾曼濾波估計的彈道位置、速度，彈丸轉速及攻角修正系數作為彈道初始諸元，解算引入攻角修正系數的四自由度彈道模型，見公式(4)。

(4)

采用濾波估計的攻角修正系數見圖5，可以看出，對于確定的某發彈丸，攻角修正系數近似為某一常值，因此引入的攻角修正系數可通過采用一段時間內的濾波均值kαE進一步提高預測精度。

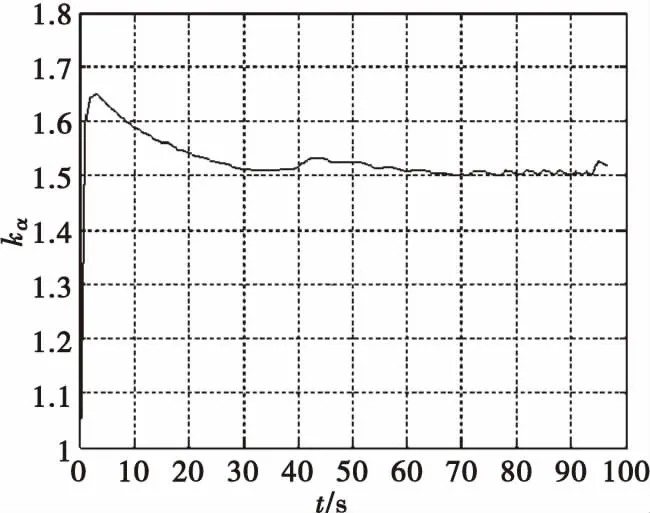
圖5 濾波估計攻角修正系數Fig.5 Estimate results of modified coefficient

通過卡爾曼濾波估計彈丸真實攻角與彈道模型解算攻角的修正系數，修正攻角進行落點預測，不僅可以減少由于攻角解算精度不高帶來的預測誤差，同時還可以減少由于彈道氣象、彈丸偏心、彈丸的質量及氣動散布等因素引起的落點預測誤差，能有效提高落點預測精度。

3 仿真和外場試驗驗證

以155 mm底排彈為平臺，分別采用仿真數據和外場試驗雷達彈道測量數據驗證基于攻角修正系數的落點預測精度。

3.1 仿真驗證

以155 mm底排彈為平臺，在初速933 m/s，射角52°(射程約36 km)，標準氣象條件下，考慮初速、射角、射向等射擊誤差，彈丸阻力、升力、質量、偏心、底排等氣動和彈丸固有誤差，氣壓、虛溫和彈道風等氣象測量誤差，解算雙旋彈道模型，采用蒙特-卡洛仿真方法生成一組縱向準確度誤差5‰X，縱向密集度1/240，橫向準確度誤差2.5 mil，橫向密集度1 mil的無控彈道。

在這組無控彈道的基礎上考慮衛星定位位置誤差10 m(1σ)，速度誤差0.5 m/s(1σ)，轉速測量誤差1‰(1σ)，采用基于攻角修正系數的落點預測算法預測彈丸落點，將預測的落點坐標與仿真的無控彈落點坐標進行比較，計算落點預測誤差，統計落點預測的CEP。圖6為300次蒙特-卡洛仿真結果，由圖可看出預測CEP為20.3 m。

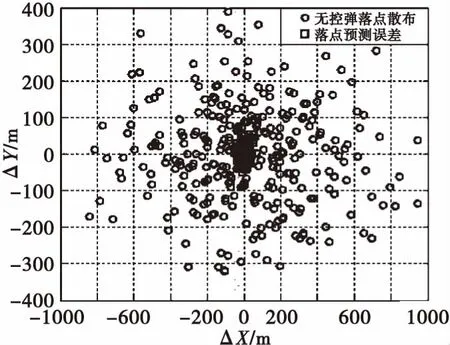
圖6 蒙特-卡洛仿真結果Fig.6 Simulation results of IPP

3.2 外場試驗驗證

基于155 mm底排彈全裝藥最大射程角(射程36 km)外場試驗雷達跟蹤數據，實測氣象數據，采用基于攻角修正系數的落點預測算法預測彈丸落點，將預測的落點坐標與實測落點坐標進行比較，計算落點預測誤差，將四發彈丸的橫縱向預測誤差進行統計，評估預測精度。

圖7為不同時刻各彈丸的射距和橫偏的預測誤差，可以看出橫縱向落點預測的絕對誤差從出炮口后約70 s開始小于50 m，從90 s開始小于30 m。圖8為采用修正系數修正攻角和不修正攻角兩種落點預測方法不同時刻四發彈丸落點預測精度，可以看出采用修正系數修正攻角能有效提高彈丸落點預測精度，其落點預測CEP從70 s開始小于50 m，從85 s開始小于30 m，最終CEP可優于20 m。

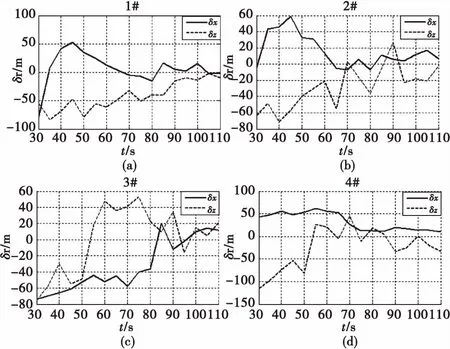
圖7 不同時刻各彈丸的射距和橫偏的預測誤差Fig.7 Down range and cross range IPP error

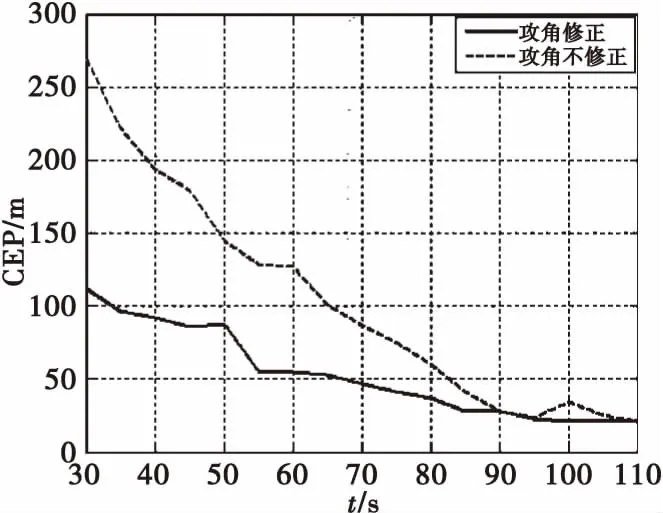
圖8 不同時刻四發彈丸落點預測精度Fig.8 IPP CEP

4 結論

本文提出了基于攻角修正系數的落點預測方法。該方法以引入攻角修正系數的四自由度彈道模型為狀態模型，衛星定位測量的位置、速度和磁傳感器測量的轉速為量測量構筑量測方程，采用擴展卡爾曼濾波估計攻角修正系數，然后基于攻角修正系數解算四自由度彈道模型預測彈丸落點。155 mm底排彈最大射程仿真和外場試驗數據驗證結果表明，采用修正系數修正攻角預測落點能有效提高彈丸落點預測精度，預測CEP可優于20 m，可推廣應用于中大口徑系列榴彈。