考慮再制造設計水平的多期閉環供應鏈網絡均衡

張桂濤，曲簫宇,戴更新，胡勁松，王永波,3，孫 浩

(1.青島大學自動化與電氣工程學院，山東 青島 266071；2.青島大學商學院，山東 青島 266071；3.空軍青島航空醫學鑒定訓練中心，山東 青島 266071)

1 引言

由于全球環境惡化和資源短缺的出現，再制造和閉環供應鏈在學界和業界備受關注。再制造生產活動減少了對資源的需求，同時降低了廢棄物產生量[1-3]，對環境的影響大大降低，從而有利于環保目標和可持續發展戰略實現，因此再制造閉環供應鏈研究和實施具有重要意義。

再制造復印機與原材料生產的復印機相比，在材料、勞動力和能耗方面節省20%，廢棄物減少35%[4]，對核心部件的回收和再利用能夠節省大約40～60%的成本[5]。鑒于此，美國、歐盟和我國均采取立法的方式要求企業對產品進行回收和再制造[6]。在2015年的5月和9月，國務院出臺和印發《關于加快推進生態文明建設的意見》、《生態文明體制改革總體方案》，在國家戰略的高度上對資源回收和利用提出了具體要求。在該背景下，生產企業在實踐中已紛紛開始進行再制造活動[7-9]。

同時，在新產品制造過程中，把產品設計成未來有利于再制造的樣式，已經在一些企業中出現(業界稱之為DFR， 即“Design for Remanufacturing”)，這其中包括施樂、柯達和通用等公司。如施樂提倡在產品的設計中，形成易拆卸、耐用和可再利用的理念[10]；柯達在高速復印機方面采用更貴的、可再次使用的不銹鋼部件代替一些塑料部件[11]。隨著再制造產業的發展，目前我國制造商亦逐步將其植入到產品的設計過程中[12]。Xu Zhizheng等[13]的研究考慮了政府對產品的監管，采用低碳多目標最優化設計產品來滿足各方面的要求。Yang等[14]分析了早期的再制造設計對再制造過程的影響，并提出了一種基于模糊TOPSIS方法的設計支持工具以方便產品的再制造設計。

在產品設計階段考慮其未來的可再制造水平，無疑會對制造商的產品生產策略、再制造過程乃至全球的資源可持續發展產生重要影響。正如Gehin等[15]所指出的，閉環供應鏈高效實施的一個重要方面是將來自于EOL策略的約束嵌入至早期的新產品設計中。但實際上，很多企業尤其是制造商對核心部件可再制造水平設計過程中應考慮哪些因素以及如何確定最優設計水平仍缺乏理論指導和有效的分析工具，從而導致其對DFR策略尚心存疑慮。BOSCH Tools管理者坦承需要更為專業的工具來做出更有效的再制造決策[16]。

另一方面，由于質量和可靠性方面的差異，消費者對新產品和再制造品的評價不同[17-20]，通常消費者對再制造品的評價相對較低。因此采用定量研究方法分析再制造活動對產品可再制造設計水平的影響以及消費者對新產品和再制造品的不同評價對閉環供應鏈定價策略的影響，不僅有助于企業決策者們消除疑慮，而且能夠提高整個閉環供應鏈的系統績效。已有文獻的研究主要集中在鏈式供應鏈，亟待將有關研究拓展至考慮競爭的供應鏈網絡。

此外，考慮到當前同類企業間競爭加劇，同時企業所在供應鏈間業務交叉，使供應鏈結構呈現為分層次的網絡，包含眾多企業和需求市場，企業間競合關系共存，企業是理性決策者，目標是追求利潤最大化。網絡中同類成員間開展非合作競爭，并形成Nash均衡狀態。如何獲得該均衡條件是學界和業界關注的重要議題之一。目前絕大多數研究局限于單個制造商、單個零售商或單個回收商的閉環供應鏈，缺少對成員間競爭因素的分析，而競爭因素可能是企業從事再制造活動并獲取利潤的主要動力。少數學者針對制造商或者零售商內部存在競爭的閉環供應鏈網絡展開研究。Nagurney和Toyasaki[21]利用變分不等式等理論建立了廢舊電子產品的均衡模型。采用同樣的理論方法，Hammond等[22]針對制造商和需求市場兩層的閉環供應鏈網絡建立均衡模型并對重點參數進行了靈敏度分析。Yang Guangfen等[23]則針對第三方回收模式建立了閉環供應鏈網絡均衡模型，楊玉香等[24]在EPR制度下針對零售商回收模式建立了閉環供應鏈網絡模型，與此相類似，本文的模型中廢舊品回收也由零售商來承擔。然而，文獻[22-24]均是針對靜態環境下閉環供應鏈網絡均衡問題的研究。現實中供應鏈內部要素和外部環境不斷發展變化，因此閉環供應鏈網絡必然是一個動態系統，成員的最優決策也必然考慮到相關因素，如生產成本和市場需求等，在多個規劃期的變化，此時決策者需通過相應的庫存調整、前瞻性地對各期的產品可再制造水平進行動態決策來實現其多期總利潤最大化。為描述該動態決策過程，本文擬將整個決策時間離散劃分為多個規劃期，假設某些參數在單個規劃期內相對穩定，而相鄰規劃期之間則發生變化。Zhang等[25]構建了多規劃期環境下的閉環供應鏈網絡均衡模型，但該研究假設新產品和再制造品無差異，且未分析產品可再制造水平對再制造決策的影響。張桂濤等[26]結合雙渠道閉環供應鏈網絡，在多期決策環境下，研究了實體和電子交易渠道間存在競爭，消費者對兩種渠道有不同偏好的供應鏈網絡均衡問題。產品設計方面，Qiang Qiang[27]在2規劃期框架下，探討了考慮再制造設計水平的閉環供應鏈網絡均衡問題，但其網絡僅由制造商層和需求市場層構成，且未考慮多期決策中較為關鍵的庫存調整策略，另外兩期的再制造設計水平亦被假設完全相同。事實上，制造商的產品再制造設計水平具有明顯的動態性，如在2期環境下，第1期要考慮到第2期的再制造成本等因素，而第2期即為最后1期，無需考慮其對未來的影響，因此2期的再制造設計水平顯然不同。如前所述，市場中的消費者對新產品和再制造產品的評價不同，因而愿意支付的價格也存在差異，實際中消費者的需求是變化的，該因素也需要在動態模型中才能得以較為完整的描述。因此，針對閉環供應鏈網絡，考慮消費者對兩類產品的不同評價，在多期情形下研究具有競爭的網絡成員的最優行為，以及由此達到供應鏈網絡Nash均衡是非常有意義的。

在多個規劃期環境下，在考慮同類成員競爭的基礎上，針對制造商、零售商和需求市場組成的閉環供應鏈網絡，其中政府規定最低的再制造設計水平，制造商可采取各期再制造設計水平相同和不同兩種方案，并委托零售商回收需求市場的廢舊品，對新產品和再制造品采用差異定價策略；零售商同時兩種產品。通過變分不等式描述網絡成員最優行為，重點分析網絡成員均衡狀態下再制造設計水平動態決策、新產品和再制造產品動態生產和定價決策，以及相鄰規劃期間的庫存轉移決策，以期為企業實踐和生產運營決策提供理論支持。

2 問題描述與符號說明

2.1 問題描述

考慮一個多期閉環供應鏈網絡，各制造商生產同質產品，網絡成員包括M個制造商、N個零售商和K個需求市場。第1期采用原材料進行生產，為便于下一期的再制造，需對本期的產品可再制造設計水平進行決策；各制造商把產品批發給零售商銷售，依據供需情況決策庫存轉移量；在第1期末，零售商把回收的廢舊品銷售給制造商，全部用于第2期的再制造生產活動中。在第1期，制造商把產品經各零售商銷售給各需求市場，需求市場的消費者購買新產品并消費后產生廢舊品，其中一部分由零售商負責回收，然后全部銷售給制造商，用于其再制造活動。第2期往后，制造商一方面繼續生產新產品并決策其可再制造設計水平，另一方面開展再制造活動，其再制造產品標有明顯標識“再制造產品”，市場上的消費者對兩種產品的評價不同，因此其批發價格也不同。制造商同時把新產品和再制造產品批發給零售商，并根據市場供需情況決定兩種產品轉移到下一期的庫存量；零售商從各制造商處以不同價格批發新產品和再制造品，然后對兩種產品分別定價，以差異化價格銷售給消費者，期末回收廢舊品；消費者對兩種產品的評價不同，因而愿意支付的價格也不同。

對于研究的最后1個規劃期，則不需考慮再制造設計水平對再制造成本的影響，且其前期生產的產品均需在最后1期銷售完畢，因此最后1個規劃期的決策情況與之前規劃期的決策有明顯的不同。

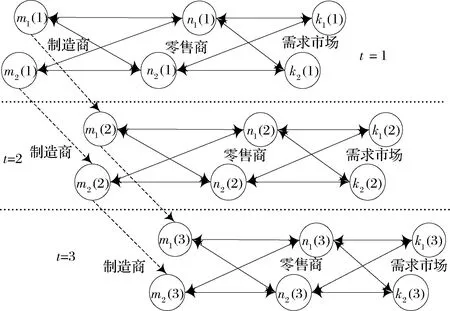
圖1 包含三個規劃期的閉環供應鏈網絡

包含2制造商、2零售商、2需求市場，3個規劃期的閉環供應鏈網絡見圖1。圖中符號n1(2)表示第2個規劃期的第1個零售商，其余符號可同樣理解。下面對圖1中交易和庫存轉移等活動進行說明。正向活動：從制造商到零售商的前向連線表示產品的批發，第1期只批發新產品，第2、3期同時批發新產品和再制造品；零售商與需求市場間的連線，從零售商指向需求市場方向表示產品的銷售，第1期只銷售新產品，第2、3期同時銷售新產品和再制造品；逆向活動：從需求市場到零售商再到制造商是產品的回收過程；跨期活動：制造商在相鄰規劃期間的連線表示新產品跨期轉移庫存和廢舊品的跨期使用。

為研究方便，給出以下假設：(1) 制造商生產過程中，由于使用廢舊品可以節約成本，因此優先采用廢舊品進行生產，該假設符合實際情況并與已有文獻一致[23]；(2)文中涉及的生產與交易函數均為連續可微凸函數[24]；(3)銷售的新產品只進行一次回收[26]，即只進行一次再制造；(4)假設各期的廢舊品回收率相同(外生常量)，該假設可很容易地擴展到各期的回收率不同的情形[27]；(5)決策變量右上角的“*”表示該變量的最優值。

2.2 符號說明

t：某一規劃期，t=1,2,…,T；

m：某一制造商，m=1,2,…,M；

n：某一零售商，n=1,2,…,N；

k：某一需求市場，k=1,2,…,K；

α：每期回收率；

ε：政府給零售商的單位回收補貼；

βv：原材料轉化率；

βu：廢舊品的可利用率；

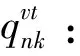
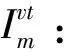
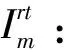
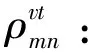
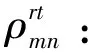
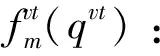
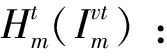
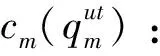
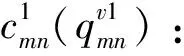
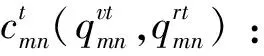
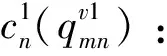
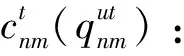
θk：需求市場k的消費者對再制造品的評價系數，θk∈(0,1]；

3 模型構建

3.1 制造商層的最優行為及其均衡

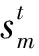
(1)

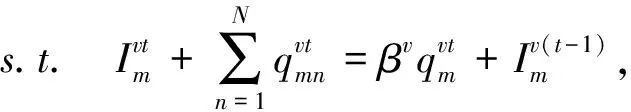
(2)

(3)

(4)

(5)

(6)

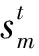
?(qv,qu,Q1,Q2,Q3,s,Iv,Ir,η1,η2,η3,η4,η5)∈ΩM

(7)

其中

式(7)的第7項和第8項表明，制造商對兩種情形的產品可再制造設計水平進行決策。

3.2 零售商層的最優行為及其均衡

根據市場供需狀況，零售商在規劃期初從制造商批發新產品和再制造品，并向消費者銷售。在期末回收經消費者使用而產生的廢舊品，其目標為實現其自身利潤最大化，且其利潤目標可表示為：

(8)

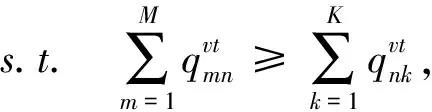
(9)

(10)

(11)

(12)

(13)

(14)

約束(9)和(10)表明，向各需求市場銷售的新產品和再制造品數量應小于或等于其從各制造商批發的相應產品數量；約束(11)和(12)表明需求市場在各期的需求將得到滿足；約束(13)表明零售商銷售給各制造商的廢舊品數量不能高于上一期銷售給消費者的新產品數量乘以可回收因子α，α可解釋為各需求市場產生廢舊品的平均可回收比例；約束(14)說明決策變量非負。

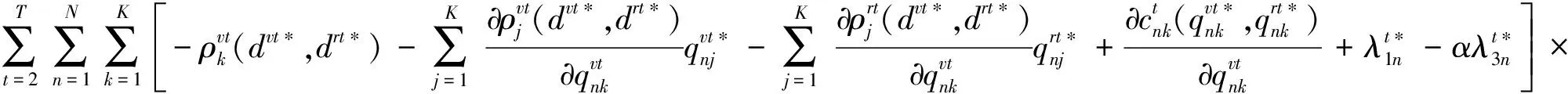
(15)

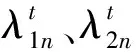
3.3 多期閉環網絡均衡模型

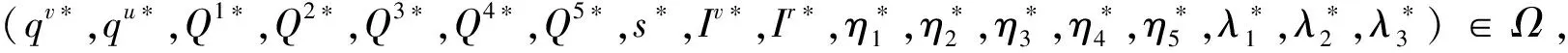
?(qv,qu,Q1,Q2,Q3,Q4,Q5,s,Iv,Ir,η1,η2,η3,η4,η5,λ1,λ2,λ3)∈Ω

(16)

其中Ω=ΩM×ΩN。

各層決策者都達到Nash均衡狀態時，供應鏈網絡即達到Nash均衡狀態，因此很有必要在凸規劃條件下討論解的存在性和唯一性，附錄給出了式(16)解的性質有關證明。

4 算例分析

算例采用圖1所示的供應鏈網絡結構和演化過程，3個規劃期，每類成員各2個，在該供應鏈網絡結構中，有決策變量96個。

本文采用修正投影收縮算法[29]求解。該算法設計簡單，迭代步長固定，收斂快，能同時獲得模型中26個Lagrange乘子，便于計算內生價格變量，可滿足所建模型的求解要求。

基本參數：迭代步長為0.01，迭代終止條件為10-10，變量初值為[0.5]122×1的列向量。模型參數：α=0.3，ε=0.2，βv=0.95，βr=0.9。引入參數p1m、p2m分別表示制造商m在可再制造設計水平方面進行的投資對生產和再制造的影響因子，其值越大(小)表明單位投資對生產成本的影響越大(小)。其余函數形式如下：

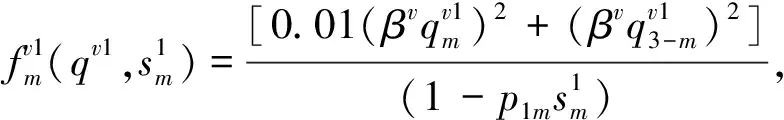
t=2,3, ?m；

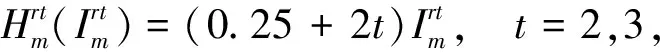
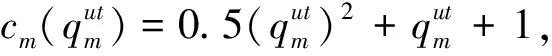
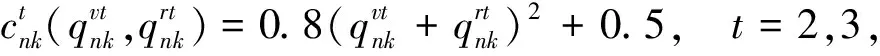
t=2,3, ?k。

本文主要針對再制造投資影響因子對可再制造設計水平和企業利潤的影響進行對比分析，并結合消費者對再制造品的評價系數、政府規定的最低可再制造設計水平等方面進行分析。具體而言，針對情況(1)p1m=1，p2m=0.6:0.2:1.6變化時的均衡狀態，結果列于表1中；(2)p1m=1，消費者對再制造品的評價系數θk=0.2:0.05:0.8變化時，網絡中制造商和零售商利潤、制造商兩種產品的生產量、庫存、新產品可再制造設計水平等關鍵變量的變化走勢如圖2至圖5所示；(3)sd=0.3，p1m=1，p2m=0.6:0.2:1.6變化時，制造商和零售商利潤、制造商新產品可再制造設計水平等關鍵變量的變化走勢圖如圖6、圖7所示。

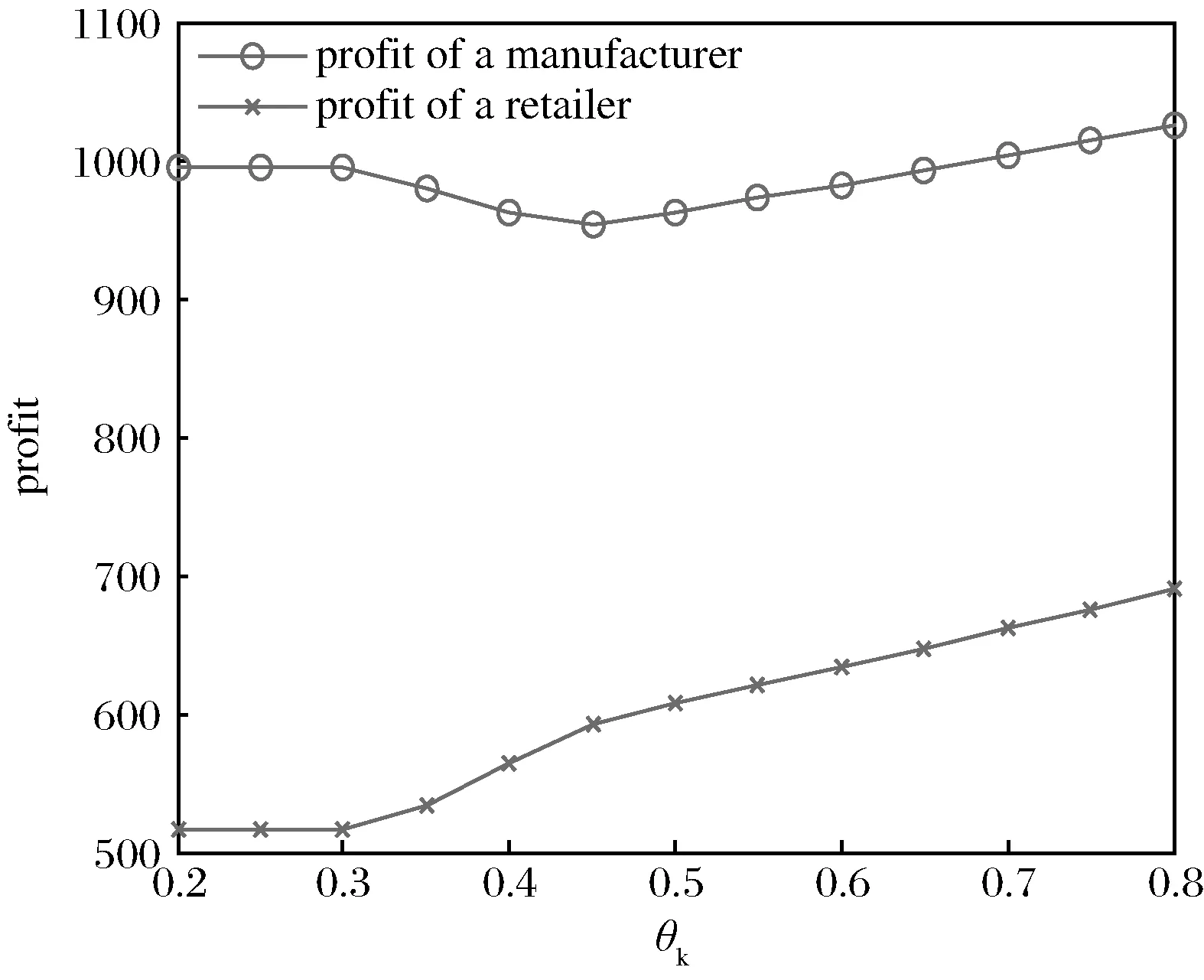
圖2 制造商和零售商利潤走勢圖

圖3 產品生產量走勢圖

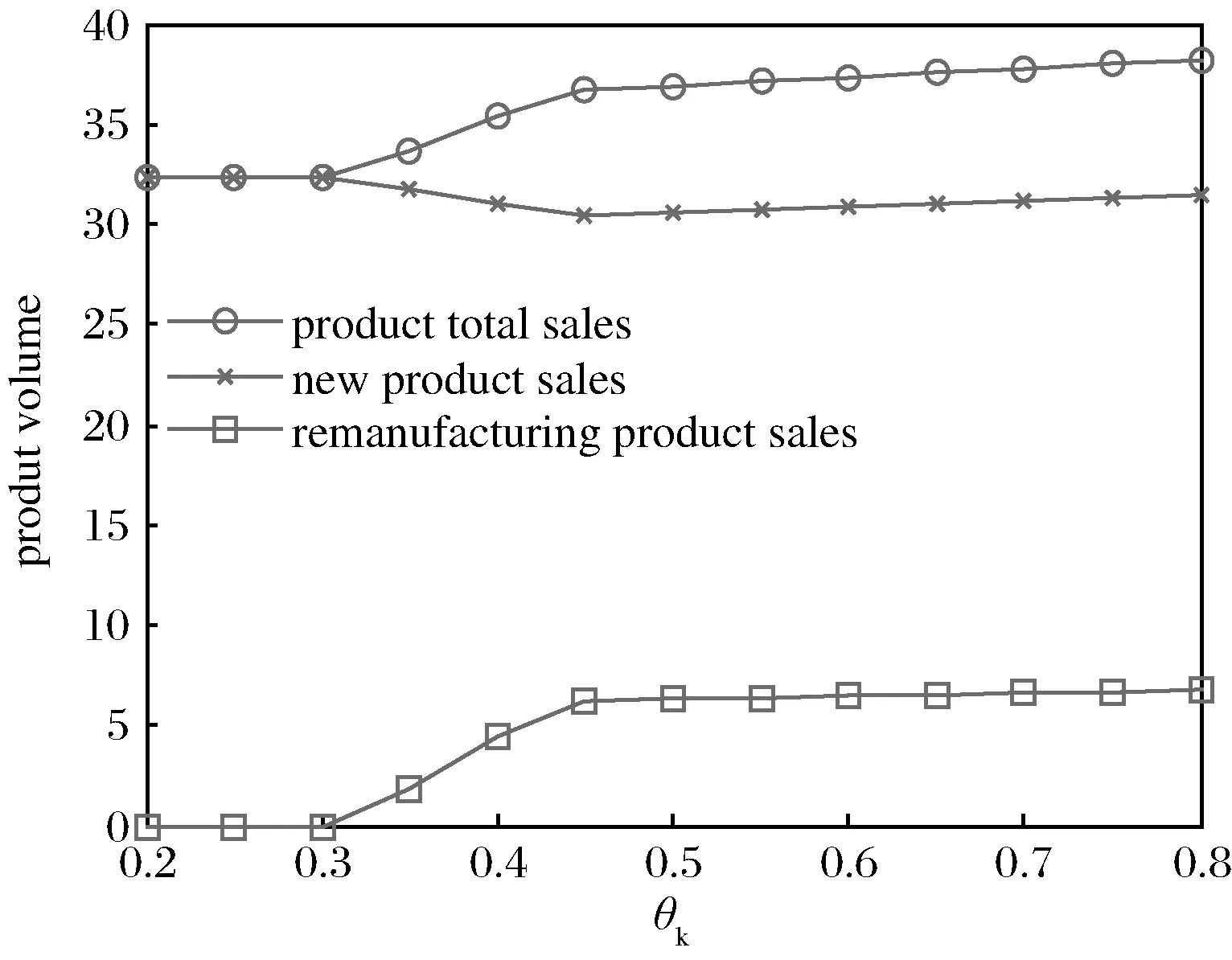
圖4 產品庫存量走勢圖

圖5 可再制造設計水平走勢圖

圖6 制造商可再制造設計水平走勢圖

圖7 制造商和零售商利潤走勢圖

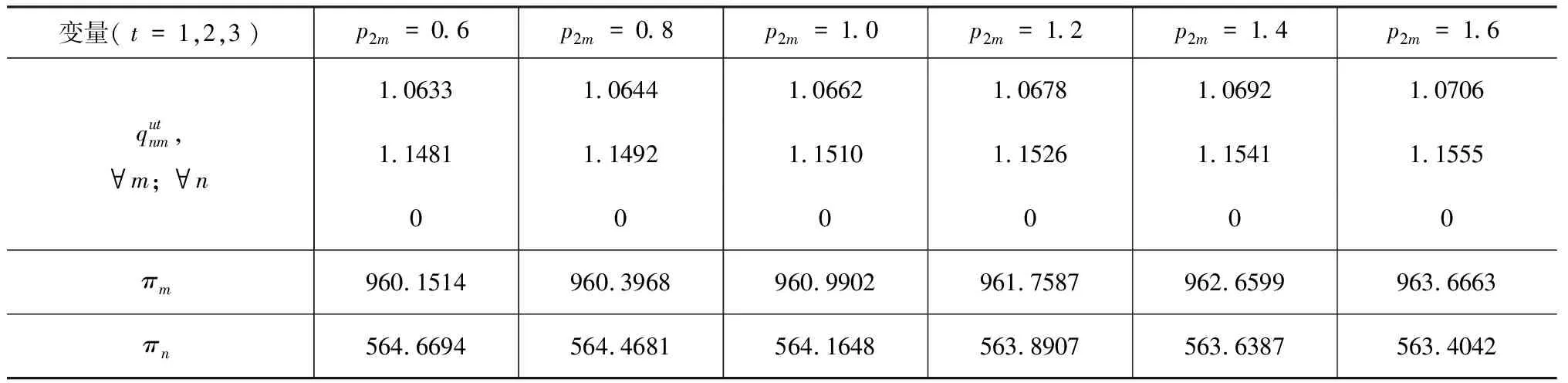
特別地，當p2m=0.6時，sm=0，說明此時再制造活動對制造商的作用不大，沒有必要進行再制造設計。而隨著p2m的增加，sm逐漸變大，說明制造商有必要進行再制造設計，且p2m越大，則越要提高再制造設計水平。

圖2表明制造商利潤在θk=0.3之前保持恒定，然后先減后增，最小值發生在θk=0.45附近；其原因為：當θk<0.3時，由于消費者對于再制造產品的認可程度太低，制造商根本無動機從事再制造；而當θk>0.3之后，再制造產品對新制造產品的蠶食程度已不容忽視，迫使制造商不得不進行產品的可再制造性投資(換言之，此時若制造商仍不從事再制造將將遭受更多的利潤損失)，另由再制造成本的函數形式易知其開始時增加較快，導致在0.3<θk<0.45的區間里制造商從再制造產品中獲得的收益無法彌補其成本的增加，因而利潤減少；而隨著θk

表1 考慮再制造設計水平的多期閉環供應鏈網絡隨p2m變化時的均衡結果

續表1 考慮再制造設計水平的多期閉環供應鏈網絡隨p2m變化時的均衡結果

進一步增加至θk>0.45之后，制造商從再制造中獲取的收益進一步增加，同時再制造成本增速變緩，所以制造者利潤持續增加。零售商不進行產品的生產再制造，其受益于再制造品接受程度θk的提高，利潤一直增加。

圖3表明當θk<0.3時，市場中僅有新產品，而后出現兩種產品共存的情況，新產品的生產量在0.3<θk<0.45區間內減少，然后保持基本穩定；相反，再制造產品的生產量在區間0.3<θk<0.45內增加，然后保持基本穩定；兩種產品的總量在θk>0.3后一直增加。

圖4則說明：隨著再制造品接受程度θk的提高，制造商將在第二期末減少新產品庫存并增加再制造產品的庫存以備在第三期銷售。

觀察圖5可以發現，在θk=0.3之前，可再制造設計水平均為0；在θk>0.3后，開始迅速增加，并在θk=0.45附近達到最大值，之后又緩慢地降低。且對于θk=0.45，對應的圖2中制造商的利潤為最低點，對應的圖3中該點為新產品產量快速減少至幾乎不減少的轉折點，同樣也是再制造產品從快速增加至幾乎不增加的轉折點。

5 結語

本文在多個規劃期情景下，考慮了制造商從事再制造時規劃期間不同的再制造設計水平設計方案。針對由制造商層、零售商層和需求市場層構成的多期閉環供應鏈網絡，利用變分不等式建立Nash博弈均衡模型。并借助修正投影收縮算法求解。算例中分析了供應鏈網絡均衡狀態隨p2m變化的結果、消費者對再制造品的評價系數對供應鏈網絡均衡狀態的影響、政府規定的強制性可再制造設計水平約束和單個需求市場的再制造品評價系數對企業利潤和再制造設計水平的影響。研究發現，p2m的增加使得再制造設計水平增加，并可使得供應鏈網絡的整體狀況變好，這就要求企業增大對再制造生產技術的投入，且p2m的增加能促進原材料的充分利用，符合可持續發展戰略的要求；政府的強制性再制造水平約束將在一定程度上影響企業的最優決策；消費者對再制造品的評價可使制造商的利潤先減小再增加，即當消費者對再制造品的認可程度從較低水平增長至中等水平的過程中，因再制造產品價格提升所帶來的利潤增加額無法彌補提高可制造性水平所增加投入的成本，這就要求制造商不要因暫時的利潤下降就完全否定消費者對再制造品評價增加的作用，待消費者的評價進一步增加后，利潤將迎來轉機。

由于產品的再制造設計需要把產品生產、銷售并回收以后，經較長時間才能在生產過程中反應出成本節約的優勢，本文所建模型主要適用于制造商長期進行產品再制造的情形。在企業的實踐中，符合本文研究假設情況的企業已經大量存在且還將繼續增加。

本文的研究尚存在一些不足， 如本文只考慮了單產品流的情形和回收者是由零售商來承擔，未來可拓展至多產品流以及第三方或者制造商來承擔回收廢舊品的情形。

附錄：

變分不等式(25)解存在性和唯一性證明。

(17)

其中<·,·>表示向量內積。

證明：根據決策變量經濟學意義，所有變量非負，可再制造設計水平取值不超過1；又市場規模有上界，由式(5)、式(11)和式(12)，制造商的生產量和交易量均有界，則式(16)可行域為緊集。

根據函數可微的假設，式(17)的梯度函數連續，由標準定理，式(17)存在一個解。

嚴格單調性證明參考Nagurney[30]。