燃燒室出口溫度場多維度分析的方法研究

鄒俊 徐艷冰 王啟道 王利 宋閣

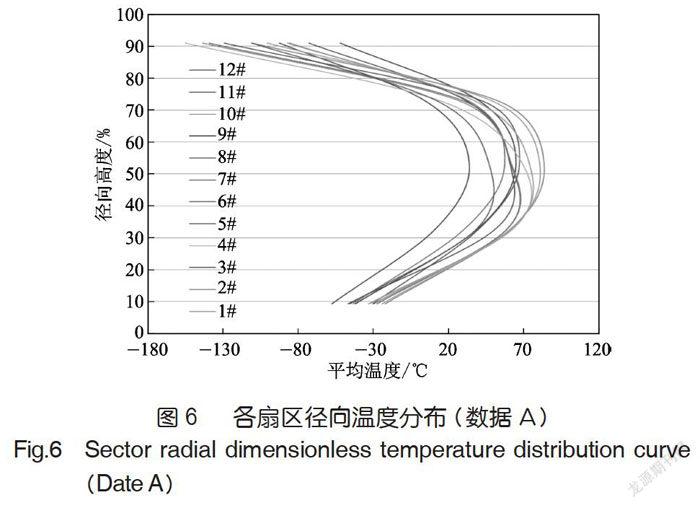
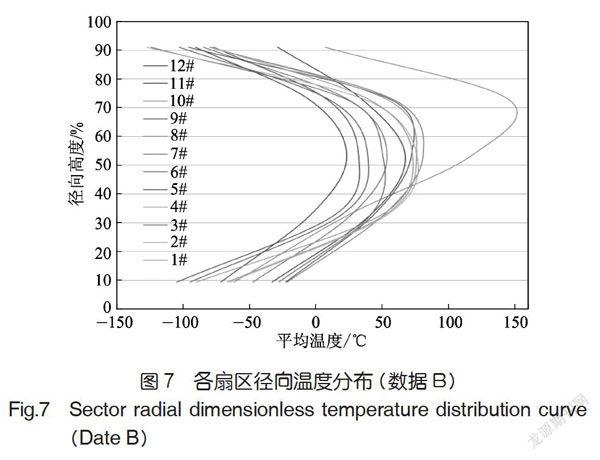
摘要：為深入挖掘燃燒室出口溫度場試驗數(shù)據(jù)中所隱含的內(nèi)在信息，基于數(shù)理統(tǒng)計理論和燃燒室出口溫度場的分布特性，總結(jié)歸納了大量溫度場數(shù)據(jù)的分析方法。并通過聯(lián)機分析處理（On-Line Transaction Processing，OLAP）技術(shù)的思路形成涵蓋整體、局部、微觀、動態(tài)4個維度的溫度場數(shù)據(jù)分析體系。并以某燃燒室的出口溫度場數(shù)據(jù)為例闡述了該分析方法的內(nèi)涵，使該溫度場數(shù)據(jù)被多角度、多側(cè)面、多層次的考察分析，驗證了該分析方法的有效性。最后對多維度分析方法在溫度場特性研究、無量綱化的比較、差異的量化分析等方面的應(yīng)用進行了初步探索。

關(guān)鍵詞：燃氣渦輪發(fā)動機;燃燒室，出口溫度場;多維度;分析方法

中圖分類號：V235A2+3 文獻標識碼：A

燃燒室是航空發(fā)動機的重要部件之一。燃燒室的出口溫度分布品質(zhì)，特別是熱點溫度，對渦輪性能和熱端部件壽命有直接的影響[1～3]，是渦輪等熱端部件運行過程中必須考慮的問題。不同國家對衡量出口溫度場分布品質(zhì)的技術(shù)指標有不同的要求，國內(nèi)一般用周向溫度分布系數(shù)（Circumferential Temperature Distribution Factor，OTDF）和徑向溫度分布系數(shù)（Radial Temperature Distribution Factor，RTDF）等來評定溫度場品質(zhì)[4]。國內(nèi)學者在溫度場的深入分析等方面也進行了很多探索研究，如劉富強等提出了用局部扇形區(qū)域徑向溫度沿葉高的分布特性這一概念來考核燃燒室出口溫度品質(zhì)[5]，王兵等對多組溫度場數(shù)據(jù)進行對比分析，建立了徑向、周向分布曲線以及可視化圖形等[6]，張樹林等引入模糊原理，介紹了一種溫度場數(shù)據(jù)的統(tǒng)計方法[7]。……