柔性平面3-RRR并聯機器人耦合動力學及模態特性研究
盛連超, 李 威, 王禹橋, 范孟豹, 楊雪鋒
(中國礦業大學 機電工程學院,江蘇 徐州 221116)
相對于串聯機器人,并聯機器人具有高速度、高加速度、高承載能力、低能耗、無累積誤差、精度高等優點,被廣泛用于航空航天、精密光學儀器、生物工程操作、精密加工機床等領域[1-5]。
隨著社會的發展,高速高效、輕型低耗成為當今全球機械產品的重要標志和發展趨勢[6-8],但輕型化的柔性并聯機器人在高速帶載情況下運行時,由于慣性力等諸多因素,各柔性桿件極易產生彈性變形,導致機器人的整體動態性能下降,影響其正常工作[9-11]。如應用在食品包裝中的拾取類并聯機器人[12]及農業采摘機器人[13-14]。
為了解決這個問題,首先要建立柔性并聯機器人動力學模型[15],徐晗[16]、余躍慶[17]、張清華[18]、張緒沖[19]分別采用不用方法,考慮不同因素建立了平面3-RRR平面并聯機器人的動力學模型。 Sharifnia[20],Zhang等[21-22]采用假設模態法分別對柔性3-PSP和平面3-RRR并聯機器人建立了動力學模型。
然而通過目前的研究發現,簡單的動力學模型極易產生過大的誤差,而精確度較高的模型往往特別復雜,導致后續振動控制難度較大甚至無法實施。因此選取合適的動力學建模方法,考慮實際邊界條件及影響因素,建立既能保證高精確度,同時又能方便求解的動力學模型具有重要的研究意義。針對上述存在的問題,本文考慮系統剛柔耦合效應及柔性中間連桿兩端集中轉動慣量影響,選取動態參數相對較少,基于系統模態特性為建模基礎的假設模態法為建模方法,通過拉格朗日方程建立平面3-RRR并聯機器人耦合動力學模型,并與有限元軟件(ANSYS)分析及模態試驗結果作比較,結果表明文中所建立動力學模型能夠有效反映系統主要振動模態,并能充分反映慣性力和耦合力對系統模態特性的影響,這對后續的振動控制及結構優化設計提供了有力的參考依據。
1 柔性3-RRR平面并聯機器人系統概況
柔性平面3-RRR并聯機器人的系統構成及坐標系如圖1所示,系統由末端運動平臺C1C2C3,固定支撐平臺A1A2A3,三條連接末端運動平臺和固定支撐平臺的支鏈A1B1C1,A2B2C2,A3B3C3組成,且三條支鏈完全相同,即A1B1=A2B2=A3B3,B1C1=B2C2=B3C3,通過轉動副將驅動連桿與柔性中間連桿以及柔性中間連桿與動平臺進行連接,其中A1、A2、A3是驅動關節,桿長A1B1=A2B2=A3B3=B1C1=B2C2=B3C3=210 mm,末端運動平臺上關節所在圓的半徑為R=68 mm。在三個驅動電機的驅動下,該并聯平臺可以完成沿x軸方向和y軸方向的平動運動以及繞z軸方向的轉動運動的三自由度運動。
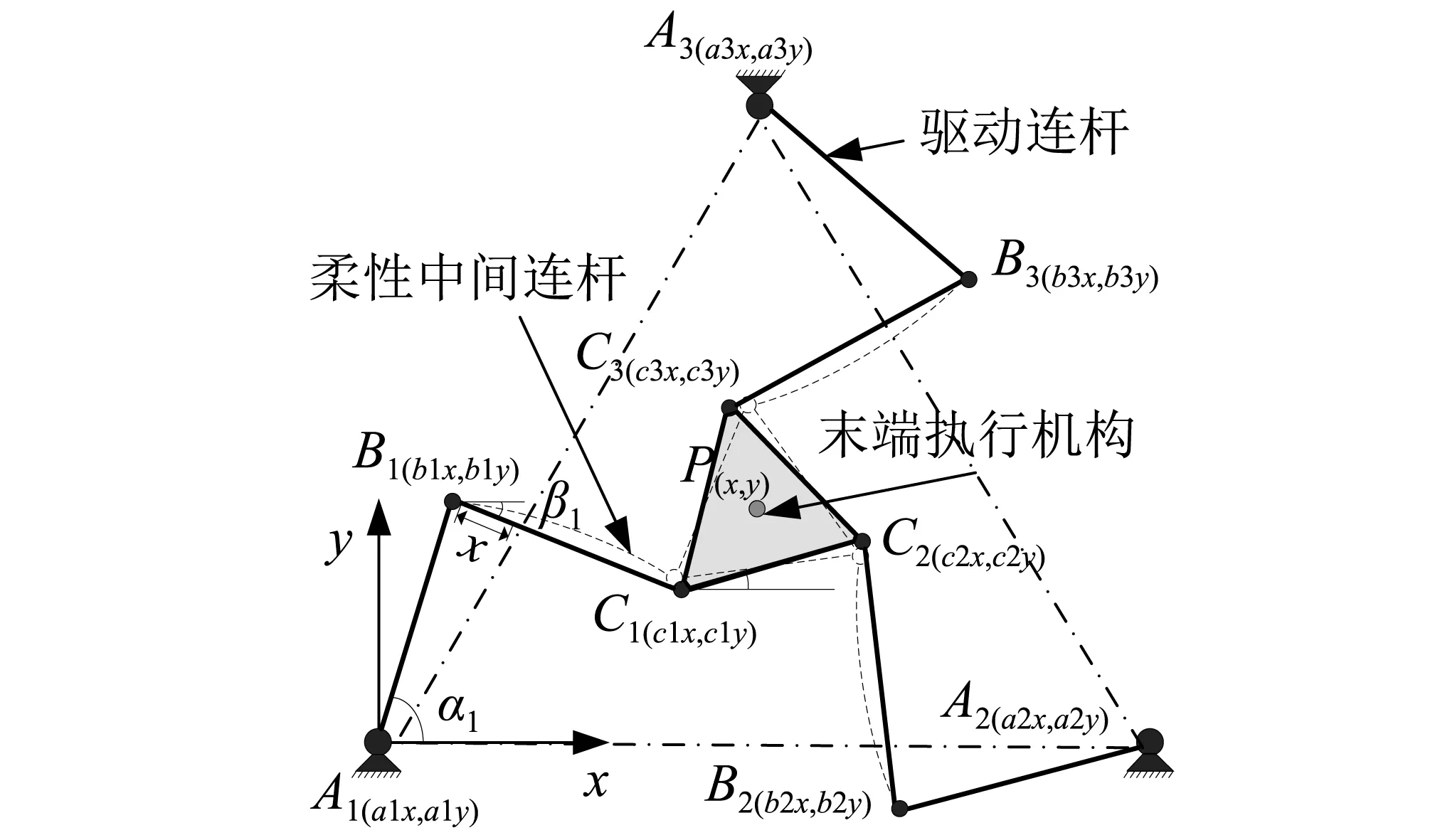
圖1 柔性平面3-RRR并聯機器人平面示意圖Fig.1 The structure diagram of the flexible planar 3-RRR parallel robot
在實際結構中,一般情況下驅動連桿橫截面積尺寸較大以保證其剛度,而柔性中間連桿截面積尺寸較小以減輕其質量。柔性平面3-RRR并聯機器人的具體材料、尺寸參數如下,加工材料為鋁合金7075,材料的彈性模量為E=7.1×1010N/m2,密度為ρ=2.81×103kg/m3,主動桿的長寬厚分別為210 mm,25 mm,10 mm,柔性中間連桿的長寬厚分別為210 mm,25 mm,5 mm,柔性中間連桿兩端的集中轉動慣量JBi=JCi=2.2×10-3kg/m2,截面慣性矩Ii=2.6×10-10m4。
機構的振動主要是由電機驅動、慣性力和移動平臺的有效載荷造成的。為了進一步確定系統的振動情況,減小不必要的計算,提高計算速度,應對柔性并聯機器人的模型作簡化。考慮到柔性并聯機器人的運動部件只有各運動支鏈和動平臺,電機、減速器及其支架等都固連在底座上,實際中為保證運行平穩,剛度支撐等要求,底座設計得比較厚重,這里可以將除運動支鏈和動平臺之外的部件視為固定,運動支鏈的主動桿的電機驅動端視為與基座固定,同時,對各支鏈和動平臺上的倒角、圓角、非必要的孔等特征也進行簡化,簡化后的柔性平面3-RRR并聯機器人有限元(ANSYS)仿真結果如圖2所示,前四階振動頻率分別為66.894 Hz、68.289 Hz、85.716 Hz、122.57 Hz,通過前四階振型發現,發生彎曲的部位主要集中在柔性中間連桿部分,第四階振型顯示,柔性中間連桿不僅發生彎曲甚至發生扭轉,這將直接導致末端運動平臺的傾覆,影響末端運動平臺的操作精度和質量,因此如何控制中間連桿的振動以及找出其共振頻率就顯得非常重要,這也為提高末端運動平臺操作精度和質量打下堅實的基礎。
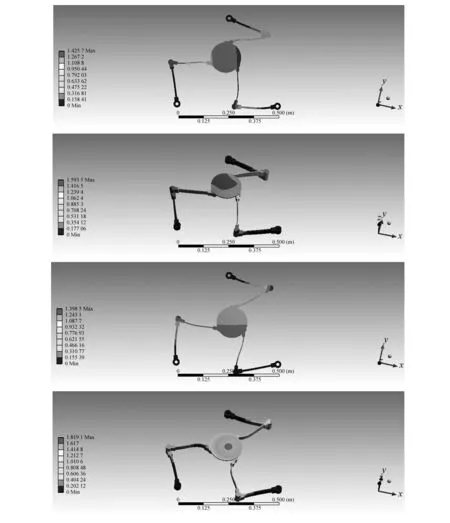
圖2 柔性平面3-RRR并聯機器人的前四階振型Fig.2 The first four mode shapes of flexible planar 3-RRR parallel robot
2 動力學建模與數值仿真
2.1 有限元分析法
在有限元分析軟件(ANSYS)中建立柔性中間連桿的物理模型,材料選擇鋁合金,柔性中間連桿兩端邊界條件設置為鉸支,并定義為柔性接觸,同時考慮兩端集中質量和轉動慣量的影響。仿真分析結果如圖3所示, 柔性中間連桿前兩階振動頻率分別為53.18 Hz,204.07 Hz。

圖3 柔性中間連桿前兩階模態振型Fig.3 The first two mode shapes of flexible intermediate link
2.2 假設模態法
基于有限元(ANSYS)分析的結果,如圖2所示,驅動連桿的振動幅值要遠小于中間連桿的振動幅值,因此在建模過程中只把中間連桿作為柔性桿處理,而其他構件均視為剛性構件。機器人系統坐標如圖1所示,其中給出了柔性中間連桿的變形和不變形兩種狀態。在建模過程中,做如下假設:①基于Euler-Bernoulli梁模型分析柔性中間連桿系統動力學特性,只考慮柔性中間連桿在運動方向的橫向振動;②相對于柔性中間連桿的長度,其橫向變形是小變形,所以方程可被線性化處理;③忽略重力的影響。為了與上述有限元(ANSYS)分析作對比,建模過程中柔性中間連桿尺寸、材料等因素均與上述有限元(ANSYS)分析法中的條件一致。考慮柔性中間連桿兩個末端軸承引入集中轉動慣量的影響,基于假設模態法,建立系統耦合動力學模型。
第i根柔性中間連桿的變形可以表達為:
(1)
式中:φij(x)為模型的振型函數;qij(t)為時間變化的模態幅度;r代表所選的假設模態。
每個柔性中間連桿都被看作是Euler-Bernoulli梁,末端運動平臺和驅動連桿均被看作剛體,柔性中間連桿的邊界條件采用兩端鉸支的約束方式,所以,振型函數φij(x)可以表示為:
φij(x)=sin(jπx/L)=sin(jπξ)=φij(ξ),j=1, 2, …,r
(2)
式中:ξ=x/L,r代表所選的假設模態,驅動連桿和柔性中間連桿的桿長均為L,x是柔性中間連桿上任意一點到Bi點的距離。
為了獲得柔性中間連桿的動力學方程,與Lagrange方程聯合建模,因此需要先求得系統的動能和勢能。系統的總動能包括驅動連桿、柔性中間連桿和末端運動平臺的動能,見式(3)。
(3)
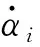
當柔性平面機器人運動時,重力沿著z軸方向并穿過一個x-y平面,所以機器人重力造成的勢能并不發生改變。系統的勢能是由柔性中間連桿的變形造成的,可表示為:
(4)
式中:Ei和Ii分別代表第i根柔性中間連桿的彈性模量和截面慣性矩。
將系統動能和勢能代入拉格朗日第二類方程
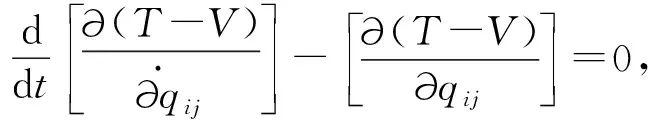
(5)
整理后為:
(6)
將其寫成矩陣形式:
(7)
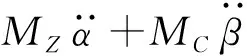
因此第i根柔性桿件的第j階響應可以表示為,
(8)
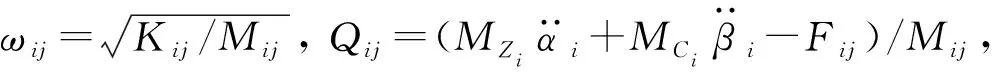
(9)
根據Duhamel積分求解上述方程,則其響應為
(10)
假定柔性并聯機器人末端執行器的運行軌跡為半徑60 mm的圓,xp=60-60cos 20πtmm,yp=60sin(20πt) mm。由于三根柔性中間連桿的參數一致,本文以柔性中間連桿1為例,研究其動態特性,柔性中間連桿1中點前兩階響應的運動仿真結果,圖4所示。
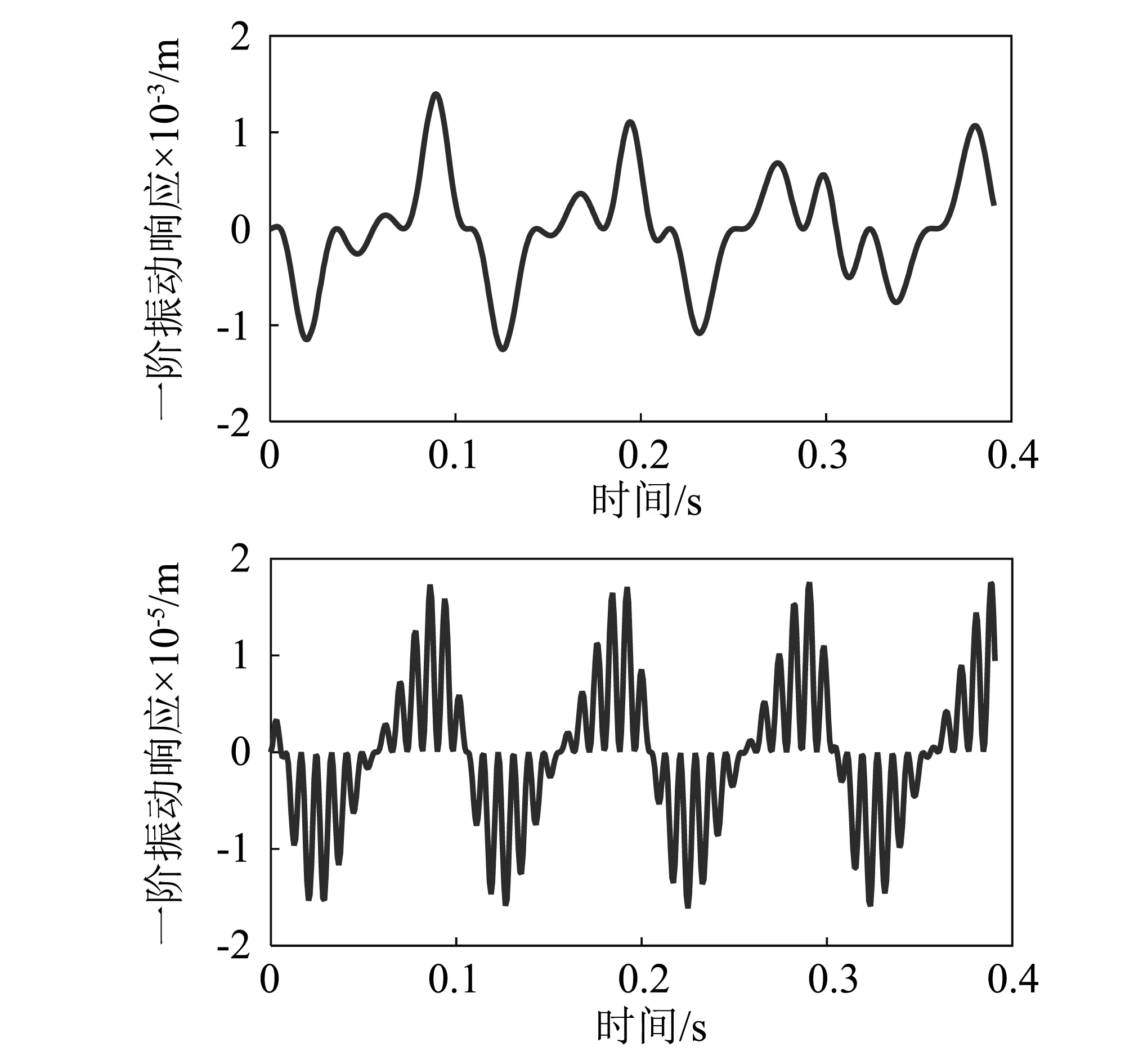
圖4 柔性中間連桿1中點處的前兩階響應Fig.4 The first two elastic vibration deformation at midpoint of the first intermediate link
通過圖4中得到的柔性中間連桿1中點處前兩階曲線可以看出柔性中間連桿的一階振動響應幅值明顯高于二階振動響應幅值,柔性中間連桿的振動響應是機器人在工作運行過程中產生振動的一個表征,為了進一步研究其振動特性,確定振動產生的頻率,降低對機器人整體性能的影響,通過快速傅里葉變換將柔性中間連桿1中點處的一階響應特性從時域轉化到頻域中,如圖5所示。
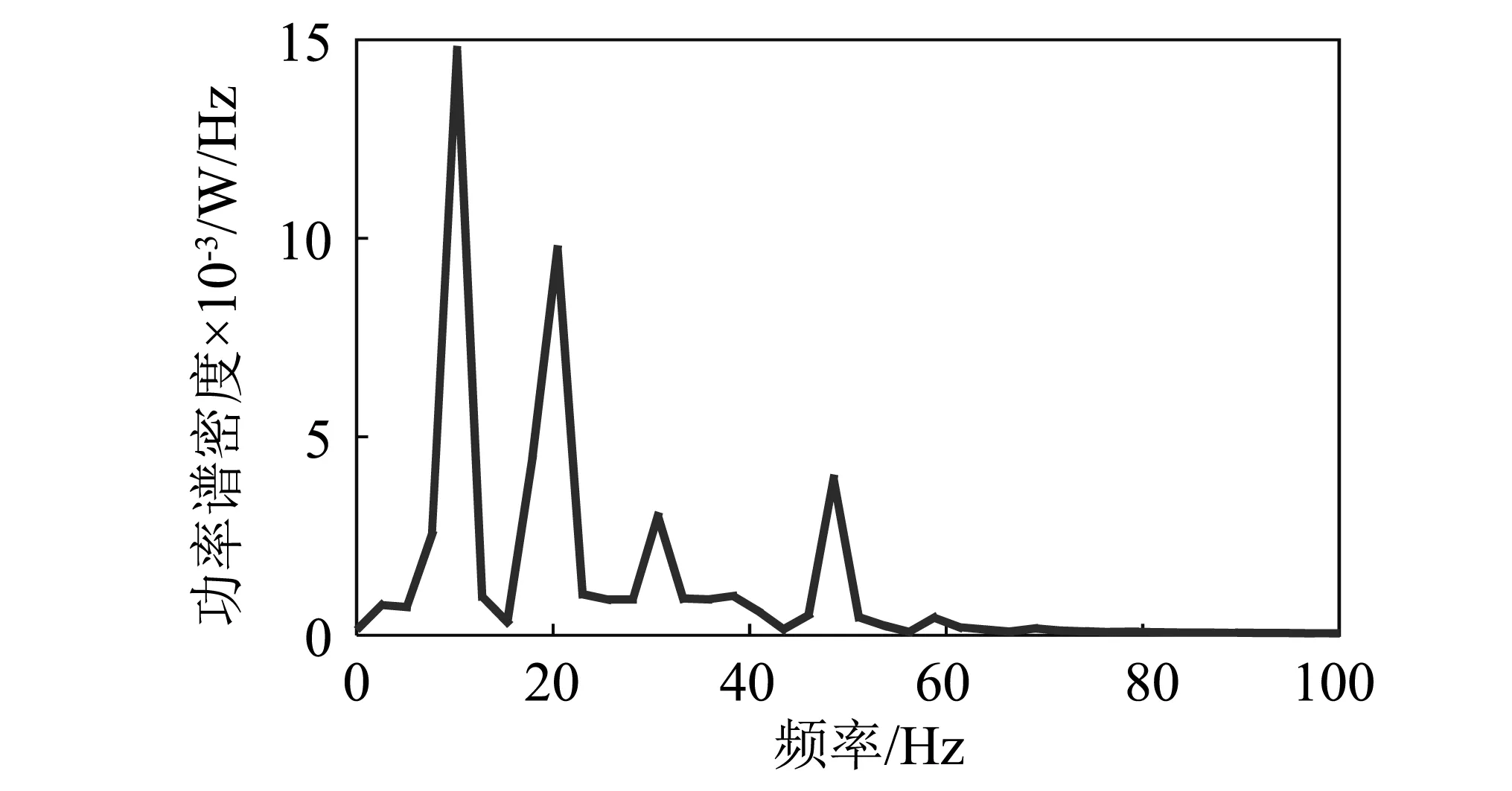
圖5 柔性中間連桿1中點處的第一階振動響應FFT變換Fig.5 FFT of the first order elastic vibration of the first intermediate link
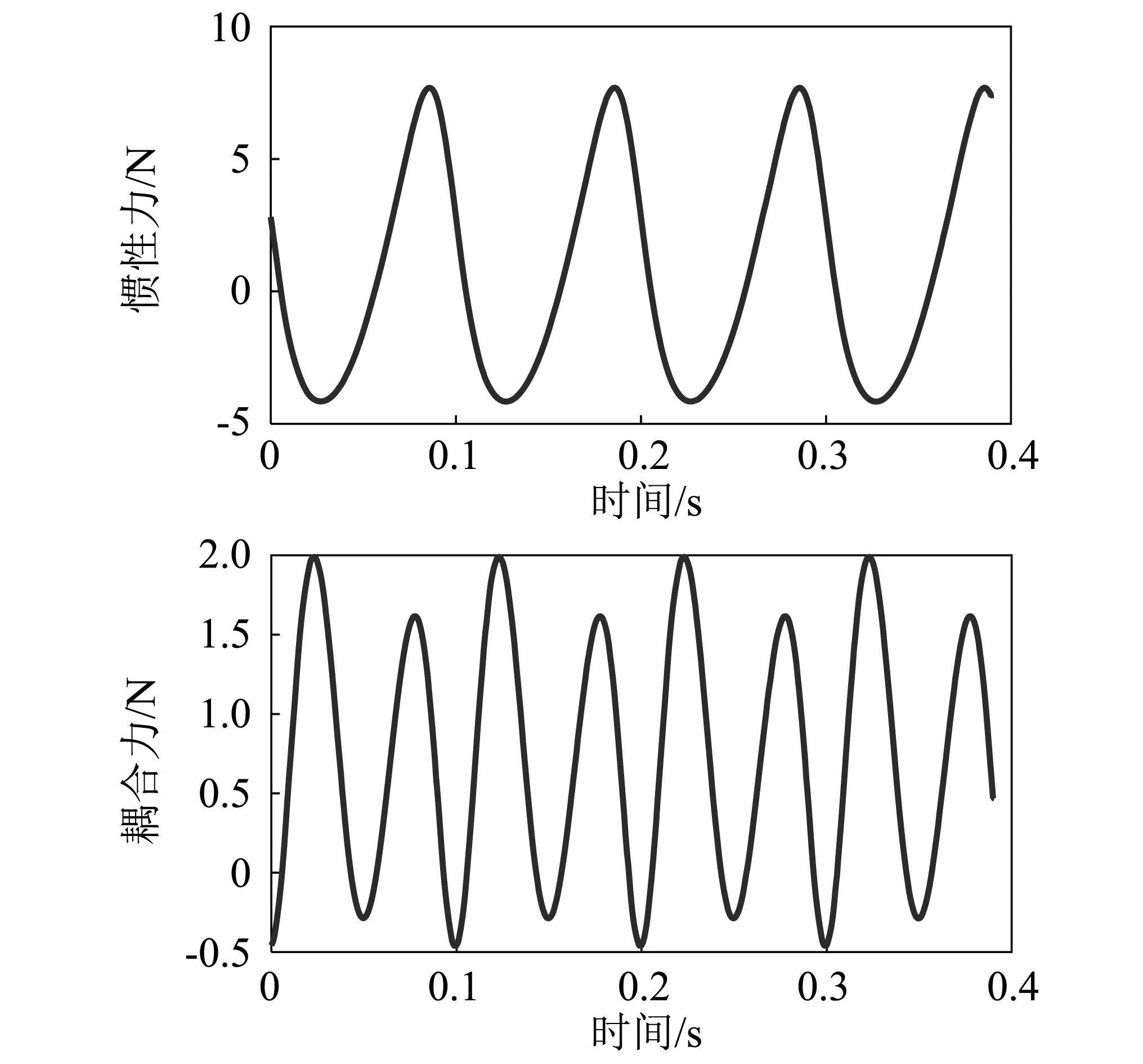
圖6 柔性中間連桿所受慣性力和耦合力Fig.6 The inertial force and coupling force of the first intermediate link
從圖5中可以看出其振動頻率主要集中在10 Hz,20 Hz,30 Hz和48.5 Hz附近,根據公式(6),可以算出柔性中間連桿在考慮轉動慣量的情況下的前兩階自由振動頻率分別為48.5 Hz,212.6 Hz,通過公式(6)還可以發現,除了自由振動,柔性中間連桿還受到慣性力和耦合力的作用產生強迫振動,慣性力和耦合力隨時間的變化曲線,如圖6所示。
為了進一步研究其振動頻率,將慣性力和耦合力動態響應曲線進行快速傅里葉變換,得到頻域特性,如圖7所示。
從圖7中得到的結果發現,10 Hz,20 Hz,30 Hz為慣性力和耦合力共同引起的強迫振動頻率,這也意味著48.5 Hz和212.6 Hz為其一階和二階自由振動頻率。
3 實驗驗證與對比分析
為了比較兩種動力學分析方法的準確性和實用性,搭建如圖8所示的實驗臺,在實驗過程中,將三個驅動電機鎖緊在初始位置,末端運動平臺在中心位置 ,柔性中間連桿均勻布置7個測點,其中測點1和7在軸承處不作測量,采用多點激勵一點拾振的測試方法,將加速度傳感器粘貼在固定測點3處,用力錘分別敲擊測點2到測點6,所測數據通過與DH5927N動態測試儀連接的加速度傳感器和力錘采集,為了使結果更具真實性,每個測點測試5次,取平均值作為試驗結果,采集數據由DH5927N動態測試儀記錄,采集記錄完成后,采用Polylscf分析法分析其動態響應,測點2到測點6的頻響特性曲線結果如圖9所示。分析結果發現一階頻率和阻尼比分別為49.992 Hz和0.043,二階振動頻率和阻尼比分別為277.813 Hz和 0.022。根據所得試驗結果表明,基于文中所建動力學模型得到的前兩階振動頻率分別為48.5 Hz,212.6 Hz,與有限元(ANSYS)得到的前兩階振動頻率53.18 Hz, 204.07 Hz相比,文中所建動力學模型得到的前兩階固有頻率更接近模態試驗結果,特別是一階固有頻率基本一致,因此文中考慮剛柔耦合因素及柔性中間連桿兩端集中轉動慣量所建立的動力學模型能較好的反映出柔性平面3-RRR并聯機器人柔性中間連桿的主要振動模態,也證明了此方法更準確,同時也證明了10 Hz,20 Hz,30 Hz的振動頻率不是系統本身擁有的頻率,而是在運動過程中慣性力和耦合力產生影響引起的強迫振動頻率,二階固有頻率產生較大誤差的主要原因主要是兩種方法在建模過程中的簡化處理,弱化了結構體對柔性中間連桿固有頻率的影響,對比兩種動力學分析方法,文中通過數學方法所建立動力學模型在分析帶有柔性中間連桿剛柔耦合系統的固有頻率及剛柔耦合效應時有更高的精度,同時由于動態參數較少,方便依托動力學模型的控制器設計。
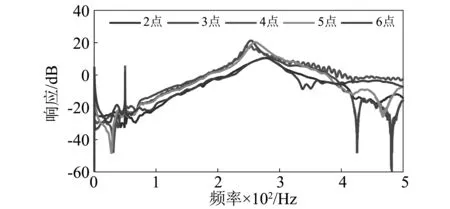
圖9 振動響應模態試驗結果Fig.9 The vibration response results of modal experiment
4 結 論
(1)相對于有限元分析軟件(ANSYS),本文基于假設模態法所建立的耦合動力學模型能夠反映集中轉動慣量及剛柔耦合效應對系統動態特性的影響,與實際更符。
(2)考慮中間連桿端部集中轉動慣量和剛柔耦合效應的影響,文中建立的耦合動力學模型可以分析耦合力和慣性力對柔性中間連桿模態特性的影響,研究結果發現,慣性力和耦合力會導致強迫振動,其頻率為10 Hz,20 Hz,30 Hz。
(3)文中所提出的剛柔耦合動力學建模方法適用于各種剛柔結合的柔性并聯機器人,所得模型精度高、易求解,解決了動力學模型復雜性問題,對需要以動力學模型為依托的控制器具有指導意義。

