基于時域譜單元的三維壓電耦合結構波傳播分析

魚則行， 徐 超

(西北工業大學 航天學院，西安 710072)

結構健康監測(Structural Health Monitoring, SHM)是指通過獲取響應信號及系統特性等信息評估工程結構受損情況、預測結構壽命的一項智能技術。其中，基于彈性導波的健康監測方法因其響應速度快、對結構影響小、對微小損傷敏感等特點，在實際工程中受到越來越多的關注[1]。彈性波在結構中傳播會發生反射、干涉、衍射、相速度頻散等現象，這給信號測量和信息提取帶來了困難與挑戰。因此，有效模擬彈性波在結構中的傳播行為和數值研究損傷對波傳播的影響現象等對發展基于彈性導波的結構健康監測方法至關重要。

壓電片因為體積質量小、頻率帶寬、易集成等特點，作為導波激發和敏感元件被廣泛應用于結構健康監測領域。研究彈性波在含壓電元件的結構中傳播時，須考慮壓電元件的耦合效應對波傳播行為的影響。鄧慶田[2]采用有限元方法研究了在縱向載荷下層合壓電桿的頻域動力學響應。李鵬[3]研究了界面、梯度功能材料等因素對波在壓電元件中傳播的影響，其對復合材料壓電設備的設計分析以及測量有重要意義。杜朝亮等[4]則采用回傳矩陣-射線方法對橫觀各向同性的壓電結構進行了頻域的波傳播分析。Wang[5]結合二維單層單元與三維多層壓電單元，建立了雙壓電晶片懸臂梁的有限元方法，研究了結構在壓電效應下的靜力學與動力學響應。Ippolito等[6-9]基于經典有限元數值模擬方法研究了壓電耦合結構中的波傳播文獻，但需要注意的是傳統有限元方法在求解結構彈性波傳播問題時存在計算耗費大、精度低等問題，很難應用于復雜結構的大規模波傳播模擬。

譜單元法最早應用于求解計算流體動力學問題[10]。這種方法結合了譜方法的快速收斂性與有限元法的復雜幾何適應性，特別適合模擬高頻、瞬態的彈性波傳播行為。Kudela等[11]將時域譜單元推廣至波傳播問題，并研究了一維結構中彈性波的傳播行為。Komatitsch等[12-13]將這種方法推廣至二維與三維結構中波傳播行為的模擬。徐超等[14]推導了任意四邊形的譜單元用于功能梯度材料結構中的波傳播問題。馮朝輝等[15]將譜單元方法與壓電效應相結合，研究了彈性波在壓電耦合結構中的傳播。但該文章僅研究了二維結構，忽略了導波在三維結構中的反射與散射，也并未結合實驗對所做的理論工作進行驗證。李富才等[16]進一步研究了壓電耦合結構波傳播分析的譜單元方法，并初步進行了實驗驗證。

近年來，宏纖維壓電復合材料(Macro Fiber Composite, MFC)作動器和傳感器因其柔性好、易于黏接于曲面結構上等優點在結構健康監測中的應用日益增多[17]。實施結構健康監測時，通常在結構的離散位置布置若干MFC壓電作動和傳感器。壓電器件激發的彈性波在結構中傳播本質上是三維的。同時，即使對薄板類結構，其裂紋、腐蝕等損傷也多發生在沿板厚度方向的局部位置，必須要對結構進行三維建模和分析才能有效地模擬彈性導波在結構中的傳播行為及其與損傷的相互作用關系。最后，針對同時考慮壓電元件和待測結構的耦合問題，對壓電、黏接層和結構組合體采用統一的三維單元來描述具有形式簡單、易于建模等優點。

因此，本文針對MFC壓電耦合結構，推導了一種三維時域壓電譜單元，并將其用于模擬彈性波在壓電耦合結構中的傳播行為。首先給出了三維壓電耦合譜單元的推導過程；然后將譜單元計算結果與有限元解進行對比，以驗證單元的可靠性與快速收斂性；最后結合實驗，驗證了譜單元方法對模擬彈性波在結構中傳播行為的有效性，并研究了導波在多壓電耦合結構中的傳播特性。

1 三維壓電耦合譜單元推導

含壓電元件的結構，其運動平衡方程可寫為

(1)

D=0 inΩp

(2)

對于壓電材料，其物理方程表示為

σ=Cε-eTE

(3)

D=eε+gE

(4)

式中： 上標h和p分別表示主結構區域和壓電結構區域。σ，f，ρ，q和D分別表示應力、體積力、密度、位移場和電位移矩陣。ε，e，g，E和C分別表示應變、耦合系數、介電常數、電場強度和彈性矩陣。

如圖1所示，與傳統有限元方法不同，譜單元采用非等距內插節點以減少龍格效應的影響，從而實現高階插值。單元內各方向的插節點由Gauss-Lobatto-Legendre多項式的零點確定，稱為GLL點。例如，在x方向，該多項式為

(5)

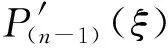
ξ1=-1
ξ2=-0.654 653 670 707 978
ξ3=0
ξ4=0.654 653 670 707 978
ξ5=1

各GLL插值點在局部坐標系下插值函數如圖2所示。

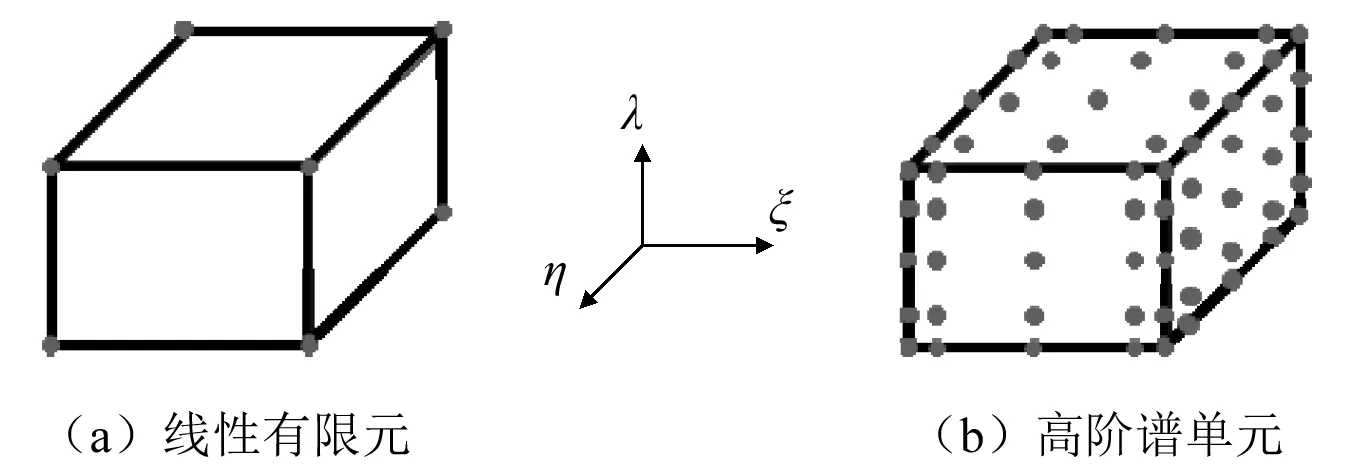
圖1 3維單元對比Fig.1 Comparison of 3D elements between

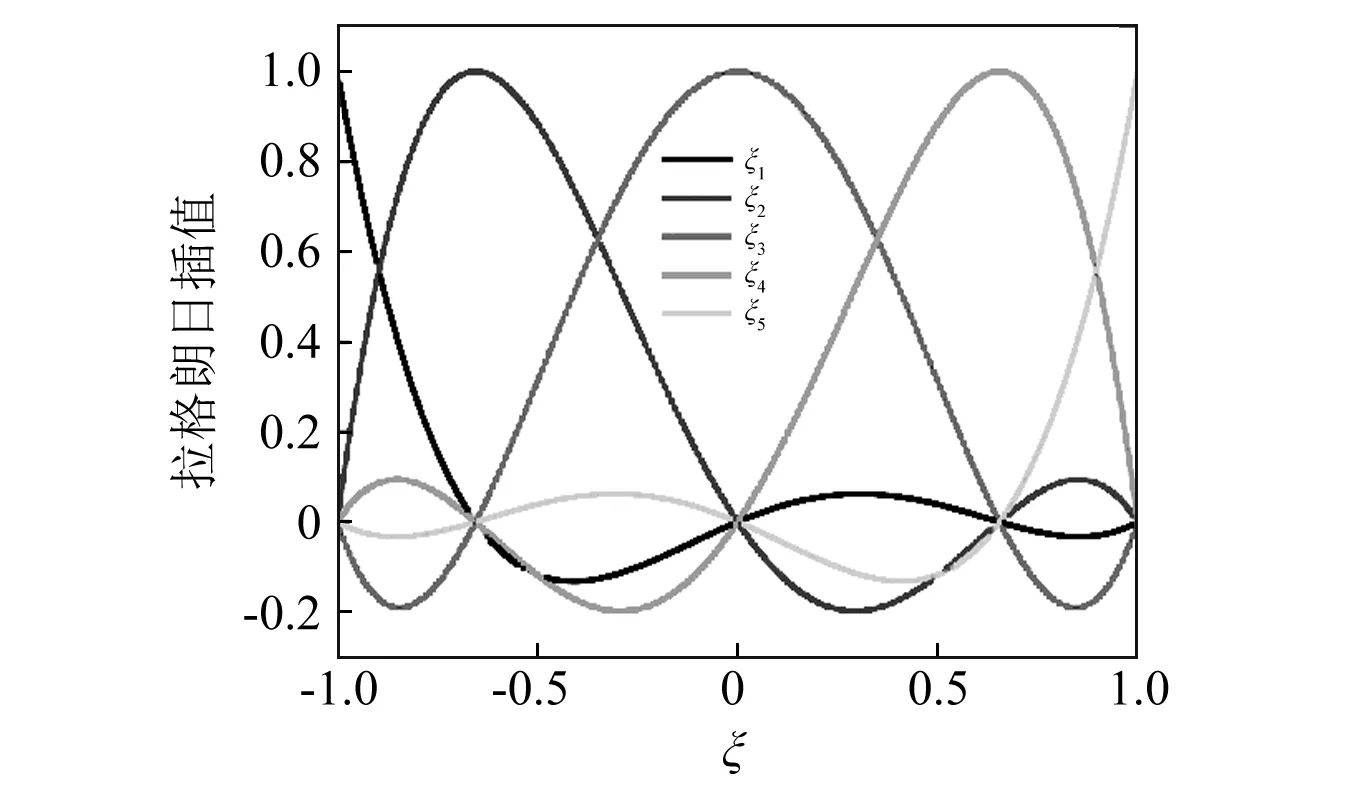
圖2 GLL節點在局部坐標系下插值函數Fig.2 Interpolation function of GLL points atlocal coordinates system

若將所得節點進行拉格朗日多項式插值，則位移場可表示為

(6)

根據小變形假設可知，應變-位移關系可表示為

ε=Buq=[B1B2…Bn]q

(7)

在電場內，電場強度與電勢的關系可表示為

E=-Bφφ

(8)

式中： 下標u和φ分別表示位移場和電場物理量，φ表示電勢場。

結合上述公式，根據Hamilton原理，可得到三維壓電耦合動力學問題的譜單元運動方程為

(9)

(10)

其中，

式中：Je為Jacobi矩陣表示單元從局部坐標系到整體坐標系的映射。ωi,ωj,ωk表示GLL積分法則在坐標方向的權重系數，由下式確定

(11)

可知，ωi>0獨立于單元，并有如下正交性質

(12)

同樣的性質也存在于另外兩個方向。因此，譜單元的質量矩陣為對角線形式，這對降低計算耗費，提高計算速度有重要的意義。

對于典型壓電材料，Kuu數量級約為108， 而Kφφ數量級約為10-11。 由式(9)～式(10)可知，若直接求解系統的控制方程，會由于兩者參數差異巨大導致與Kφφ有關的項在計算過程中由于太小而被湮沒。這會引起計算上不可忽略的誤差。為克服這種缺點，本文引入靜力凝聚法，將Kφφ有關的項凝聚掉以位移場向量表示。因此，與式(9)～式(10)可寫為

(13)

(14)

式中：KI和fA分別表示由壓電耦合引起的誘導剛度矩陣和等效節點力。

KI誘導剛度矩陣的計算中，Kφφ矩陣由定義可知為非正定矩陣。因此，KI矩陣的計算則與壓電材料的電學邊界條件相關。

(1) 壓電元件作為傳感器處于電學閉路：壓電元件上下表面接地，電勢為0，元件內不含有自由電子。可知，式(10)在電學閉路條件下可寫為

(15)

式中： 各矩陣上標為：0表示壓電元件下表面；i表示壓電元件中間層；n表示壓電元件上表面。則壓電結構中未知電勢可以表示為

(16)

則可知， 誘導剛度矩陣KI可表示為

(17)

(2) 壓電元件作為傳感器處于電學開路：壓電元件下表面接地，電勢為0，可知此時式(10)可寫為

(18)

壓電結構中未知電勢表示為

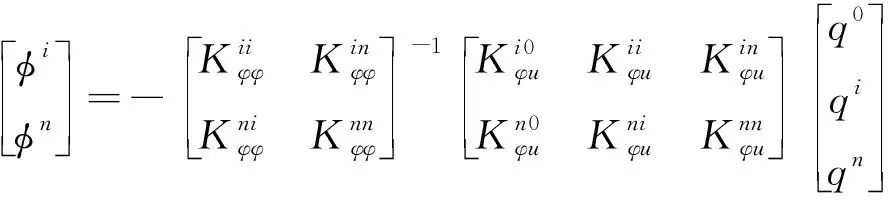
(19)

此時，誘導剛度矩陣KI可表示為

(20)

(3) 壓電元件作為驅動器：壓電元件下表面接地，上表面施加電壓V，式(10)可寫為

(21)

未知電勢可表示為

(22)

誘導剛度矩陣可表示為

(23)

其中，由上表面電壓引起的等效節點力可以表示為

fA=Kuφφ

(24)

根據線性假設，忽略由于形變帶來壓電單元上各節點的電勢變化。因此，φ矩陣中各節點的電勢由上下表面電勢場線性插值而來。Ke=Kuu+KI,Fe=f+fA分別稱為三維壓電單元的廣義剛度矩陣與廣義力矩陣。

通過組裝各單元矩陣，三維壓電耦合結構總體平衡方程可表示為

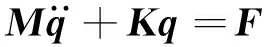
(25)

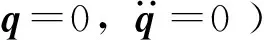
(26)

其中Δt表示積分時間步長，該算法穩定的條件為

(27)

式中：Tn表示結構系統的基本固有周期。

2 數值驗證

2.1 單片壓電耦合結構

為了驗證所推導的三維壓電譜單元能有效地模擬彈性波在壓電耦合結構中傳播行為，考慮貼壓電片的薄板結構，其幾何尺寸如圖3所示。薄板為鋁制品，壓電片采用MFC材料，長25 mm，寬10 mm，厚0.3 mm。各材料屬性如表1所示。

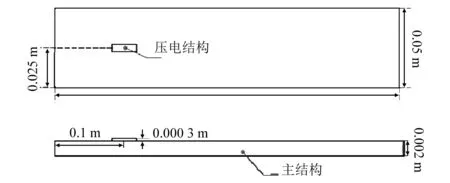
圖3 單片壓電耦合結構Fig.3 Thin palte with one MFC piezoeletric transducers

薄板結構Eνρ70 GPa0.332 700 kg/m3壓電材料C11=3.94×1010 PaC22=2.03×1010 PaC33=3.25×1010 PaC12=1.29×1010 PaC13=0.83×1010 PaC23=0.53×1010 PaC44=0.55×1010 PaC55=0.55×1010 PaC66=1.31×1010 Pae31=13.62 cm-2e33=-4.1 cm-2e32=0.55 cm-2e24=-17.03 cm-2e15=-17.03 cm-2g11=141.2g0g11=141.2g0g11=141.2g0ρ=7 000 kg/m3g0=8.854 19×10-12CV-1m-1

針對壓電元件作為驅動器與傳感器兩種情況分別分析：

(1) 工況一：壓電元件作為驅動器，將其下表面接地，上表面接入如圖4所示的電壓，激勵波形為頻率100 kHz的5周期的漢寧窗調制正弦波。采用譜單元將結構全局劃分為612個單元，單元內插節點數為4×4×4，積分時間步長選取0.01 μs。輸出監測點R(0.15,0.015,0.002)處位移-時間歷程曲線，并與傳統有限元方法對比，結果如圖5所示。

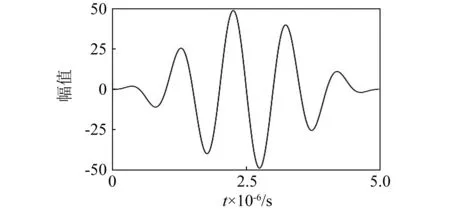
圖4 激勵波形Fig.4 The exciting waveform

圖5(a)給出了監測點R處的x方向的位移響應，圖5(b)和圖5(c)分別給出了監測點y方向和z方向的位移響應。由圖可知，在各個方向上，譜單元求得位移-時間歷程曲線與傳統有限元解能夠較好吻合，驗證了本文所建立單元的有效性，但是需要說明的是使用兩種方法所采用的網格數量有很大差別。表2給出了兩種方法在相同精度結果下所采用的計算規模。通過對比可知，譜單元方法能以極小的計算代價獲得相當高精度的解。

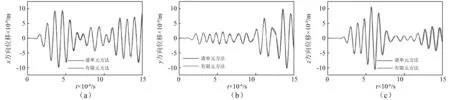
圖5 R點處位移-時間歷程曲線Fig.5 Time histories of displacement at point R

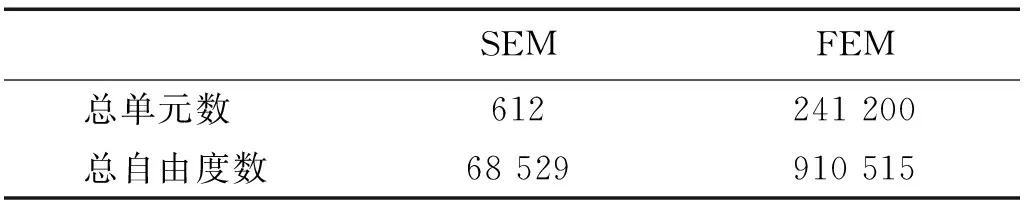
SEMFEM總單元數 612241 200總自由度數68 529910 515

在模擬高頻導波在結構中的傳播行為時，有限元方法對網格密度有很高的要求。通過對比可知，在相同精度的結果下，譜單元方法將結構全局劃分的網格數遠小于傳統有限元,兩種方法對應的總自由度數也相差較大。因此，譜單元在研究彈性波在結構中傳播規律時，能夠大大降低計算耗費與必要的存儲空間。

(2) 工況二：壓電元件用作傳感器，將其下表面接地，在薄板末端的中點(0.3,0.025,0.002)施加一垂直沖擊載荷，激勵波形仍如圖4所示的100 kHz調制正弦波。網格劃分與積分步長的選擇與工況一保持一致。輸出壓電片上表面平均電勢，并與傳統有限元方法對比，結果如圖6所示。

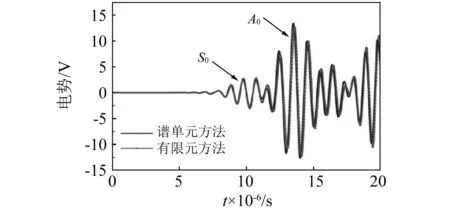
圖6 壓電片上表面平均電勢Fig.6 The average voltage of the top surface ofpiezoelectric sensor

由圖6可知，當壓電元件作為傳感器時，譜單元解與傳統有限元解能夠較好地吻合，說明了所建立譜單元的有效性。但兩種方法所得結果在A0模式存在微小的相位偏差，且譜單元解波速略快于有限元解。這是由于在求解高頻響應的A0波時，有限元方法對厚度方向的網格尺寸提出了更高的要求，即在每個波長內，傳統有限元法需要更多的節點數才能使結果趨近于解析解，而譜單元法則可以較少的節點快速收斂于精確解。如在Kin等對這一現象也有所提及，根據Richardson外插公式與有限元理論方法，在每個A0波長內，有限元方法需至少80個節點才能近似于解析解，但譜單元法僅需10個節點即可收斂于精確解。

綜上所述，本文所建立的三維時域譜單元能夠有效地模擬彈性波在壓電耦合結構中的傳播行為，且相較于傳統有限元方法，譜單元法在計算規模上具有顯著的優勢，并且精度更高。

3 實驗驗證

3.1 壓電耦合實驗結構

在結構健康監測中，通常采用一個壓電片作驅動器，激勵起彈性波在主結構中傳播，另一個壓電片作傳感器，檢測彈性波的傳播并生成相關的響應信號。這種“一收一發”的壓電耦合結構通常稱為pitch-catch結構。為了研究彈性波在pitch-catch結構中的傳播，考慮一黏有兩壓電片的鋁制方板，其幾何尺寸如圖7所示。

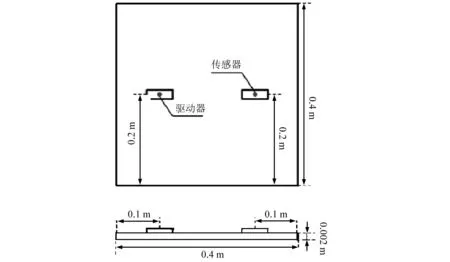
圖7 pitch-catch結構幾何尺寸(m)Fig.7 Geometry of the pitch-catch structure (m)

兩個壓電元件均為宏壓電纖維復合材料傳感器(MFC, SMART MATERIAL 公司)，壓電片長28 mm，寬14 mm，高0.3 mm。各結構材料屬性與2.1節一致。實驗裝置平臺及試件如圖8所示。鋁板處于自由-自由狀態，采樣頻率為2 MHz，其輸入信號如圖4所示，為峰值50 V、頻率100 kHz的漢寧窗調制正弦波。在實驗室環境下對該pitch-catch結構在同樣工況進行32次重復測試，測試結果重復性較好，之間差異很小。并對實驗結果進行平均，將其與數值模擬結果進行對比。

圖8 實驗平臺示意圖Fig.8 Experiment platform

在內插節點數為5×5×5情況下，計算不同網格規模的波傳播結果并進行收斂性分析，結果如圖9所示。可知，采用譜單元方法將結構全局離散為3 265個單元時，響應趨于收斂，計算結果與實驗記錄結果的對比如圖10所示。

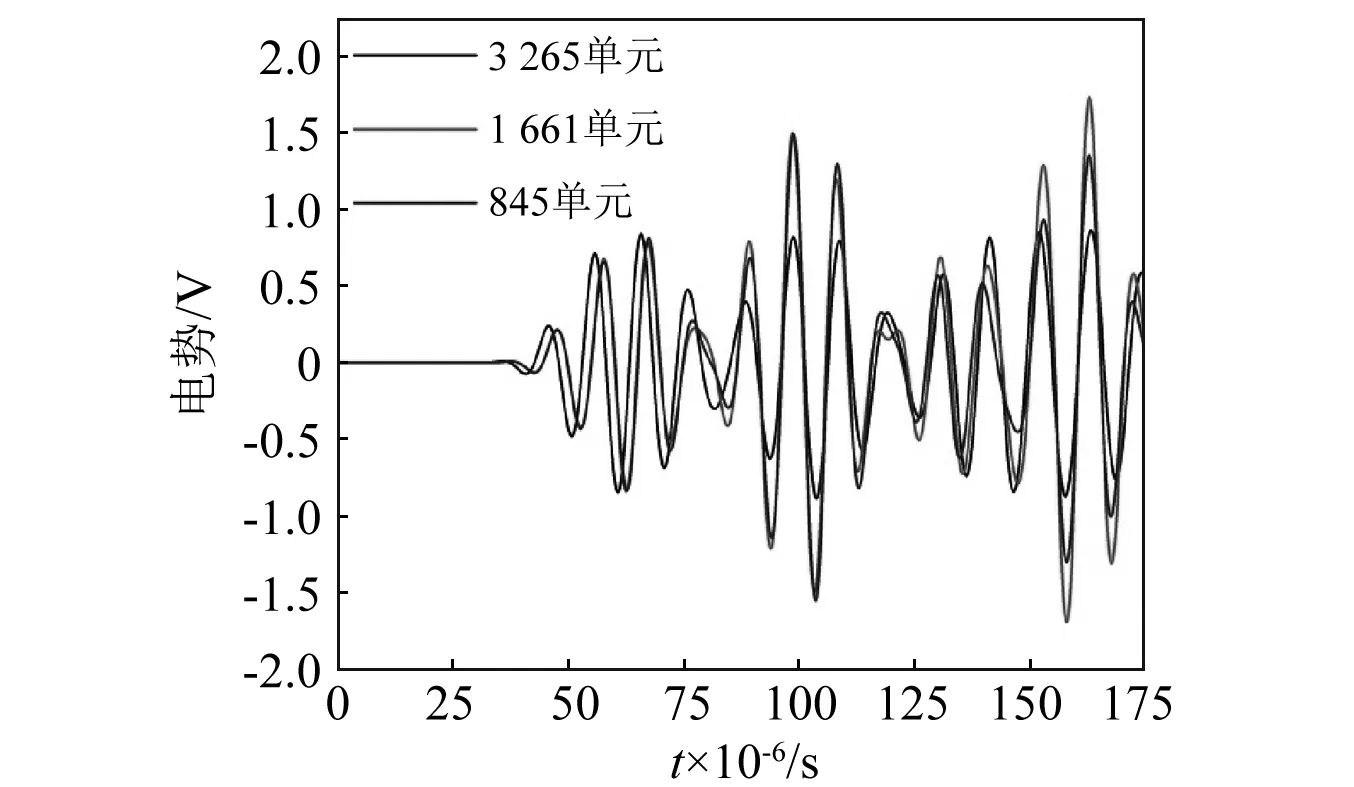
圖9 譜單元收斂性分析結果Fig.9 The convergence study of SEM

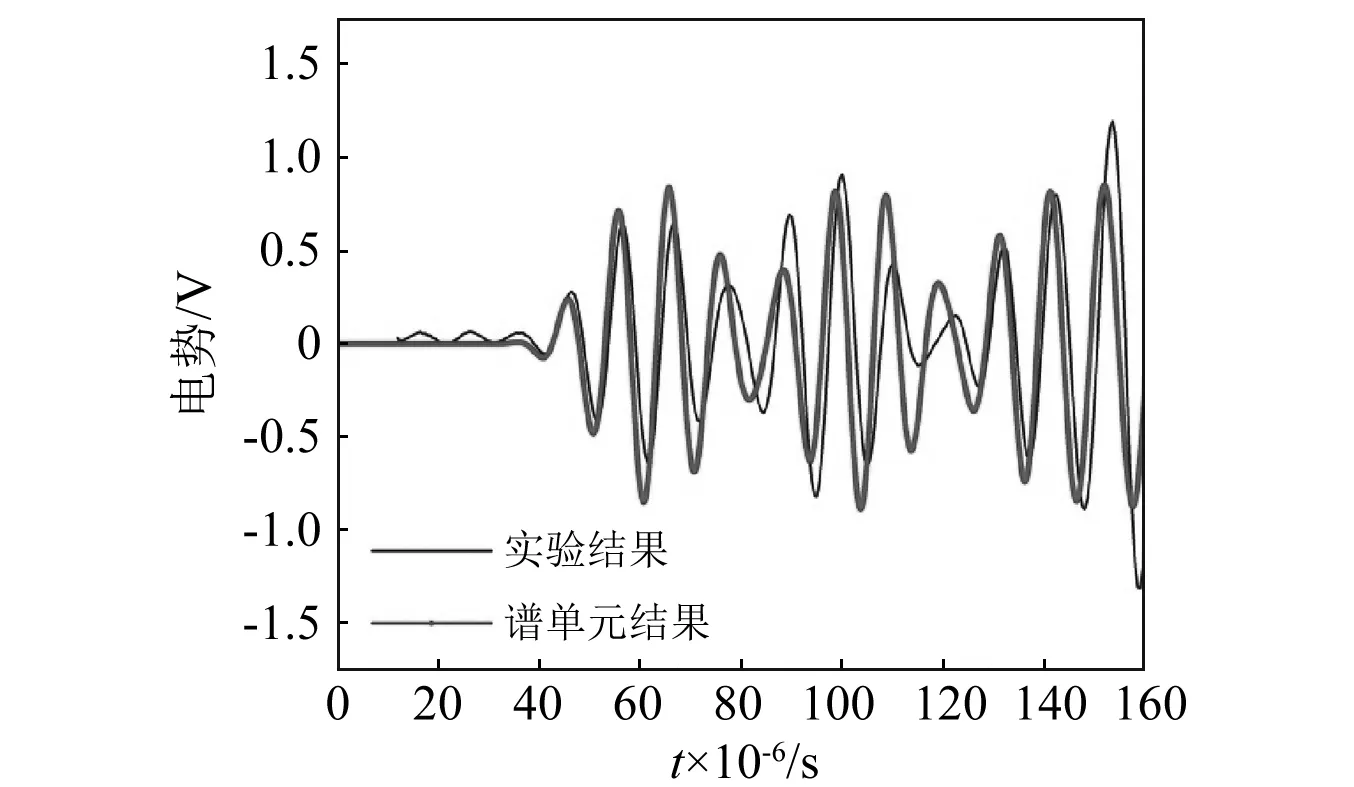
圖10 pitch-catch結構傳感器上表面平均電勢Fig.10 The average voltage of the top surface of sensor

由圖10可知，通過與實驗結果的對比，譜單元所得結果與實際情況符合較好。譜單元在模擬高頻導波傳播時，對于波速的計算尤為準確。由于在實驗過程中，采用柔性支撐來模擬試件自由-自由的邊界條件以及試件之間的膠層等因素可能造成了兩種方法的響應幅值上的差異。相較于有限元方法，本文所推導的譜單元能夠更高效、準確地模擬彈性波在壓電耦合結構中的傳播情況，對于損傷監測、沖擊識別等結構健康監測技術具有重要意義。

4 結 論

本文針對壓電元件在結構健康監測領域中的廣泛應用，推導建立了一種三維實體壓電耦合譜單元，分別研究了壓電元件用作激勵器與傳感器兩種不同工況下，結構中的波傳播行為。并結合有限元解與實驗結果，研究譜單元方法在研究波傳播問題的應用。主要結論如下：

(1) 通過與有限元解結果的比較，說明了譜單元方法能夠有效地模擬壓電元件在單獨作動荷單獨傳感兩類功能下的力學行為。通過對比兩種方法的計算規模，譜單元方法能夠大大降低計算規模，提高運算速度。相較于傳統有限元方法，譜單元法在模型彈性導波的A0模式時，能夠快速收斂到精確解。

(2) 與實驗結果的比較，說明了譜單元方法在模擬多壓電元件結構中波傳播的有效性，驗證了其用于結構健康監測的潛力與優勢。