基于諧波窗函數的橋梁振動信號分解與重構

葉 飛， 吳加權， 張馨予， 肖 馳， 馬 琨

(昆明理工大學 建筑工程學院，昆明 650500)

橋梁在公路與鐵路運輸系統中扮演著重要的角色。然而，由于受施工質量、環境、工作負荷、工作年限等諸多因素影響，必將導致結構性能下降甚至出現缺陷，進而危害到橋梁安全。因此，融合了信號處理技術的結構健康診斷(Structural Health Monitoring,SHM)成為了廣大學者關注和研究的熱點問題，它對于預防災難發生及為損傷橋梁提供廉價有效的維修方案具有積極意義。損傷檢測，是SHM的主要研究領域之一[1]。從復雜信號中提取出有效信號是進行損傷檢測的重要前提之一。

近年來，越來越多的學者選擇采用基于振動理論的研究方法開展相關研究[2-3]。這些方法主要通過研究結構在振動過程中損傷前后各模態參數(如固有頻率、模態振型、模態阻尼)的變化來進行損傷的定位識別[4]。Messina等[5]研究發現，通過研究結構固有頻率的變化，可以實現損傷檢測；Pakrashi等[6]提出了利用小波變換實現基于模態振型的直接損傷檢測方法；Hu等[7]通過對比橋梁損傷前后模態振型變換進行了損傷識別。在此基礎上，眾多學者又開發出了許多敏感性更高的損傷檢測指標。郭惠勇等[8]對基于模態應變能的3種損傷指標進行了對比分析；Bayissa等[9]用彎矩響應功率譜作為損傷指標對二維板類結構進行了損傷檢測；余竹等[10]利用Lipschitz指數在識別信號奇異性上的優越性，結合位移模態的小波變換對裂縫梁的損傷識別效果進行了研究。

雖然，眾多學者在損傷方法及檢測指標方面做了大量的研究工作，但不可回避的一個現實問題就是，作為分析基礎的數據即檢測信號(位移、速度、加速度等)的有效性問題。在實際檢測過程中，由于外界或儀器本身干擾，往往信號的信噪比較差；或者，由于結構損傷程度較輕，因此損傷造成的信號變化非常微弱；再或者，由于測量時間較長，使得損傷造成的信號變化在整個測量數據中占比較少，導致信號處理過程中被其他信號淹沒。因此，信號的質量對后期的分析結果及精度有較大影響。為了克服以上問題，學者們引入了信號處理相關技術，并與傳統工具相結合進行了大量的研究工作。孫增壽等[11]將小波變換與曲率模態相結合利用小波變換系數殘差構建損傷檢測指標實現了橋梁損傷定位；余竹等將小波變換與Lipschitz指數相結合提高裂縫損傷識別的敏感性；劉習軍等[12]運用小波變換對振動模態分析中疊加的多階模態信息進行了有效分離；Han等[13]的研究結果表明，運用希爾伯特-黃變換(HHT)結構的模態參數進行提取并進行損傷識別是可行的和有效的；Zhang等[14]利用HHT對檢測信號進行了分解得到了各頻段的頻率時間關系，并以此為基礎利用固有頻率變化率實現了多裂縫損傷的識別。

盡管小波變換與HHT技術的引入豐富了損傷檢測的方法提高了識別精度，但實際應用過程仍存在一些需要改進的地方。比如：由于許多小波母函數本身沒有明確的時域和頻域數學表達式，造成了頻段劃分時頻帶的混疊；在一些奇異信號的識別中，小波母函數的選取對信號重構的結果影響較大，小波母函數選取不當容易導致重構信號的失真[15]；小波變換的頻帶劃分必須滿足fm/2n這一約束條件的限制，導致頻帶寬度無法滿足要求；當頻帶劃分較小時，無論小波變換還是HHT都需要不斷的迭代計算，計算時間長。因此，本文提出了一種基于諧波窗函數的信號分解與重構方法，該方法對信號提取過程中出現的，信號失真、相移、頻帶劃分受限以及計算量大等問題有所改進。

1 諧波小波及諧波小波包變換

一些新的研究表明：基于信號處理技術對橋梁振動信號進行分解與重構，對提取出的低階振動信號也可以實現橋梁的損傷檢測。小波變換在信號分解、放大以及瞬態信號的檢測方面具有明顯優勢，但由于許多小波母函數本身沒有明確數學表達式且分解后易出現頻帶混疊。因此，Newland于1993年提出的一種以正交小波函數(諧波小波)為母小波的諧波小波變換。

諧波小波函數的頻域表達式為：

(1)

式中：n=2(j+1),m=2j,j∈Z+。對式(1)做傅里葉逆變換，即可得到諧波小波的時域表達式：

由式(2)可以看出ψ(m,n)(t)是一個實部為偶函數，虛部為奇函數的復小波函數，它具有零相移的特點。對于離散信號s(r),(r=0,1,2,…，N-1)，其諧波小波變換的時、頻域表達式分別為：

(2)

為了提高運算效率E. Newland給出了諧波小波的快速計算方法：首先，根據需求確定信號擬分析頻段的范圍；其次，利用式(1)計算相應頻段諧波小波的頻域表達式Ψm,n(ω)；再次，計算信號的頻譜(r)，第四，利用式(3)計算各頻段信號的小波變換頻譜值最后，對進行傅里葉逆變換即可得到相應頻段的時域信號。

(3)

根據以上公式及計算方法，可得知諧波小波(包)變換與傳統小波(包)變換相比的三大優勢：① 諧波小波(包)在頻域具有嚴格的盒形譜，避免了分解后頻帶的混疊；② 經過諧波小波(包)變換后的信號相移為零；③ 采用諧波小波(包)變換后的信號與原始信號相比，不會出現數據點數的損失。

諧波小波(包)與傳統小波(包)變換的主要區別在于小波母函數的不同，因此諧波小波變換在信號的分解過程中同樣存在分解后頻段寬度必須滿足fm/2n這一條件限制的問題(fm為分析頻率，即采樣頻率的1/2)。圖1為諧波小波(包)分解時頻段分布圖，圖中j=1時，諧波小波與諧波小波包分解的頻段劃分是一致的，當j>1時，諧波小波分解不會對大于fm/2部分的進行分解，而諧波小波包則會繼續按fm/2n繼續進行劃分。

圖1 諧波小波(包)分解頻段分布圖Fig.1 Frequency distribution of harmonic wavelet(packet) decomposition

1994年，Newland已經將二進制諧波小波(包)推廣到了廣義諧波小波(包)[16-17]。使得諧波小波(包)的頻段寬度由fm/2n變成了fm/n。這樣的頻段劃分方式，雖然可在整個頻段內對信號進行無限細分，但若擬分析信號恰好在兩相鄰頻段均有分布，則會給信號的分析帶來諸多不便。因此，諧波窗函數的構建即是為了實現頻帶的自由劃分。

2 諧波窗函數

基于廣義諧波小波(包)，本文采用構建諧波窗函數的方法進行橋梁振動信號的提取，具體方法如下：

2.1 諧波窗函數的構建

設原始信號中擬分析的頻段帶寬為B，則：

B=fh-fl

(4)

式中:fh，fl分別為擬分析頻段的頻率上限與下限。

由于離散信號s(r)在做傅里葉變換后，其頻譜具有對稱性，其實部為偶函數，虛部為奇函數。因此，在構建諧波窗函數時，其頻域數據序列也為對稱形式，其頻域圖形，如圖2所示。

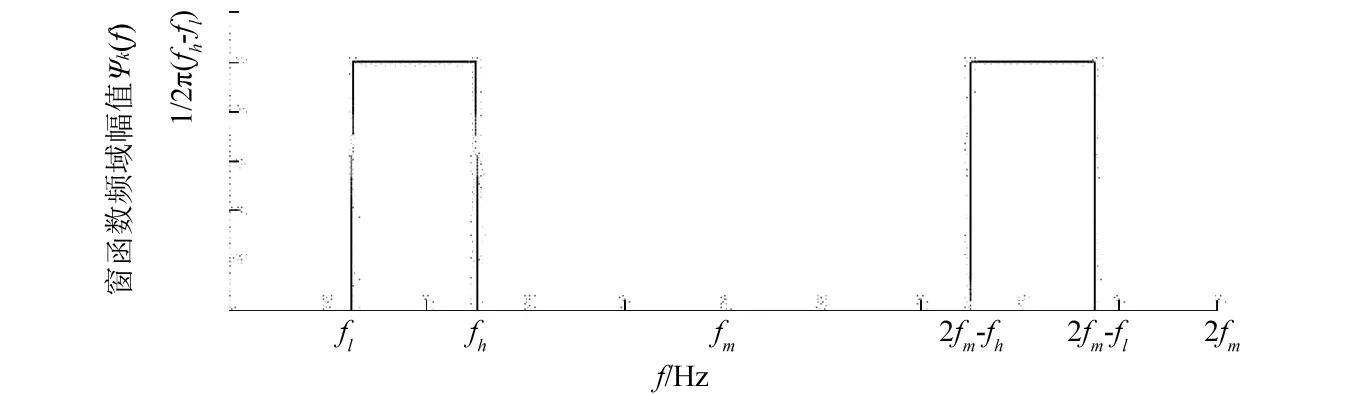
圖2 諧波窗函數頻域圖Fig.2 Frequency domain of harmonic window function

2.2 基于諧波窗函數的信號分解的實現過程

(1)構建諧波窗函數

針對橋梁低階振動信號進行損傷識別時，分析的主要研究對象為各階次固有頻率部分。因此，在根據公式(5)進行諧波窗函數在構建時，fl與fh的選擇可參照振動信號頻譜中各階次固有頻率的位置進行選擇。

Ψfl,fh(k)=

(5)

(2)對原始信號做快速傅里葉變換(FFT)

對原始信號s(r)做FFT變換，得到其頻譜序列S(k),(k=0,1,2,…，N-1)。

(3)計算分析頻段的諧波小波變換

分析頻段的諧波小波變換系數可由式(6)計算得出：

(6)

由于，FFT后的頻域數據序列具有對稱性，若需要對分析頻段的頻域信號進行分析，式(7)表達的數據序列即為諧波小波變換后頻譜；

(7)

若需要對分析頻段的時域信號進行分析，為了保證數據的完整性，則需要對式(8)表達的數據序列進行快速傅里葉逆變換(IFFT)得到。

(8)

對于廣義諧波小波變換，當頻帶無交疊時，各頻段的小波變換是正交的。諧波窗函數的構建基于廣義諧波小波，且本文分析對象為橋梁振動時各階次固有頻率所在頻段的信號，因此采用本方法進行分解后的各頻段信息也必然是正交的。另外，采用諧波窗函數分解時，與關注頻段無關的信息已全部歸零，所以分解過程中噪聲信號也一同被過濾了。

3 橋梁振動信號的諧波窗函數分解與重構實驗

3.1 信號采集

原始信號數據來自于一根600 cm×25 cm×50 cm的鋼筋混凝土梁(下文簡稱梁)的振動實驗。梁的密度為2.5×103kg/m3，混凝土保護層厚度為40 mm，受壓縱筋2×?20，受拉縱筋3×?20，箍筋?8，配置間距200 mm。梁的幾何尺寸如圖3所示。

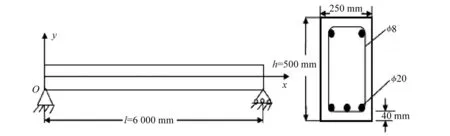
圖3 梁幾何尺寸示意圖(mm)Fig.3 Beam geometry size(mm)

實驗通過使用24磅鐵在梁頂部進行隨機敲擊的方法對梁進行激勵，使梁產生振動以采集其動態應變信號。信號采集實驗共設11個測點，每測點包含沿x方向與y方向的電阻應變計各一片(其中x方向為測量片，y方向為補償片)。實驗裝置如圖4所示。

圖4 信號采集實驗裝置圖Fig.4 Device diagram signal collection experiment

應變計均布置于梁底部，相鄰測點間距為50 cm。測點分布情況，如圖5所示。

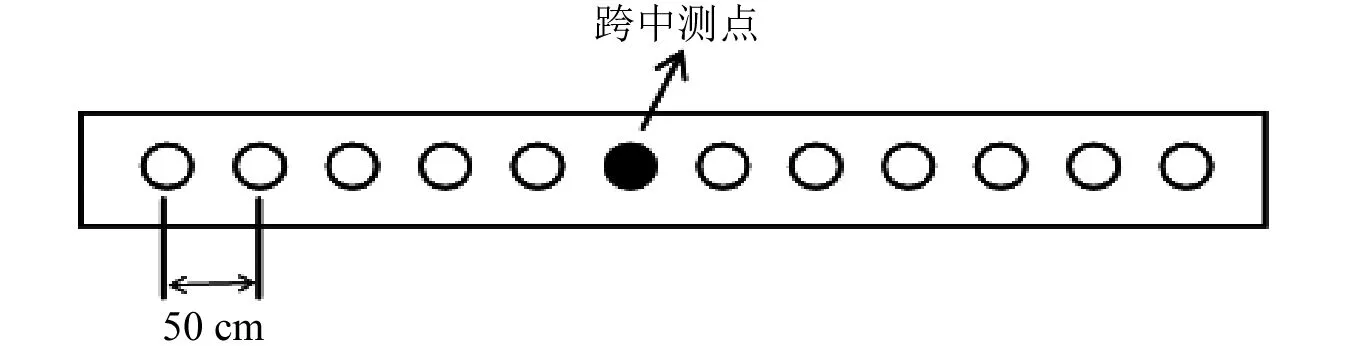
圖5 測點分布圖Fig.5 Distribution of measuring points

應變計電壓信號的采集，通過DH5922動態信號測試分析系統完成。由于各測點數據的分解與重構方法相同，下文以梁底部跨中位置處應變計測量的電壓信號數據(即圖5中實心圓點所對應測點的數據)為例展示信號處理效果。

信號采集參數設定如下：采樣頻率為2 kHz，采集時長437 s，傳感器類型為應變測量，信號類型為電壓采集,mV，采集方式為連續采集，數據點數874 448。圖6為原始信號的時域圖與頻譜圖。

改革開放四十年來，在中國新大學運動發展過程中產生的這些問題，既需要在“內涵”建設、“新大學”精神和學校定位三個“術”的方面下功夫，同時也需要在“道”的層面對新大學進行深層次的反思。

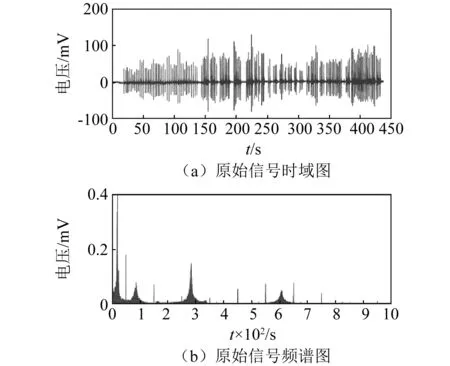
圖6 原始信號時、頻域圖Fig.6 time-frequency domain of original signal

圖6(a)為采集的原始時域信號，縱坐標為應變計采集到的電壓mV；橫坐標為時間t，s。在對時域信號做快速傅里葉變換后，我們可以獲得它的頻譜信息。由圖6(b)可以看出，梁的前五階固有頻率分別在19.6 Hz、86.3 Hz、164.9 Hz、284.2 Hz、608.3 Hz。

若要采用傳統二進制小波(包)變換進行分解，則需要對信號進行4層分解才可將5階信號分解到獨立頻帶內。分解后5階信號所在節點號及頻段范圍如表1所示。表1中小波(包)變換的頻段根據公式fm/2n劃分，諧波窗函數法的頻段，以頻率幅值下降到各階次固有頻率中心幅值的20%時對應的頻率值作為頻段的上、下限頻率(即式(5)中的fh，fl)。

3.2 一階信號分解重構后結果對比

由表1可以看出，二進制小波與小波包分解后頻段范圍對前兩階信號來說沒有區別，而對后三階及以后信號來說，小波包分解的頻段更窄，包含的干擾信號也更少。因此，本文選用小波包變換的頻帶劃分范圍，分別選用諧波窗函數與小波包對信號進行分解與重構。

表1 各階次信號分解后頻段分布情況Tab.1 Frequency distribution of decomposed five order signals

基于小波包變換對實驗信號進行分解與重構可利用MATLAB軟件中的小波工具箱完成，其實現過程如下：

1) 分別選擇小波基函數為db10小波與哈爾小波，對原始信號進行4層分解。得到16節點的小波包分解樹，第4層節點編號依次為(4，0)，(4，1)，…，(4，15)。完成對信號的分解。

3) 利用工具箱提供的單節點重構函數對(4，0)節點的信號進行重構，使其數據量由原始信號的1/16恢復為原始大小。一階信號重構完成。

基于諧波窗函數進行信號分解與重構的過程如下：

1) 構建諧波窗函數。分別設fl，fh為0 Hz和62.5 Hz，根據式(5)定義[1 0 1]型數組。

2) 利用快速傅里葉變換計算原始信號的頻譜，得到其頻譜序列。

3) 根據式(6)，將第1步定義的[1 0 1]型數組與第2步得到的頻譜序列相乘并乘以補償系數125π，得到0～62.5 Hz頻段信號的頻譜序列，完成信號的分解。

4) 對第3步得到頻譜序列作快速傅里葉逆變換，實現該頻段信號的重構。

實驗結果如圖7所示。

圖7為0～62.5 Hz頻段信號經分解重構后136.6 s～137.5 s內的時域信號，其中(a)圖為原始信號、(b)圖為哈爾小波包分解結果、(c)圖為“db10”小波包分解結果、(d)圖為諧波窗函數分解結果。由圖7可以看出：

(1)分解重構后的信號波形基本一致，但與原始信號相比高頻信息(即波形中毛刺)明顯減少。說明兩種方法均實現了一階振動信號的提取。

(2)(b)、(c)圖的最大振幅在50 mV左右，與原始信號最大振幅接近，(d)圖中最大振幅為20 mV左右。其原因在于經過4層分解后，利用小波包變換得到的單節點的數據量降為了原始數據量的1/16(54 653個數據)。小波工具箱中單節點重構函數在重構過程中利用插值算法將數據量恢復到了原始數量(87 448個數據)，使得信號能量增加，振幅增大。諧波窗函數法在分解與重構的整個過程中數據量始終無損失，無需插值。在將高頻信號去除后，必然出現信號能量減小，振幅降低的情況。說明諧波窗函數法分解重構后的結果更接近真實信號。

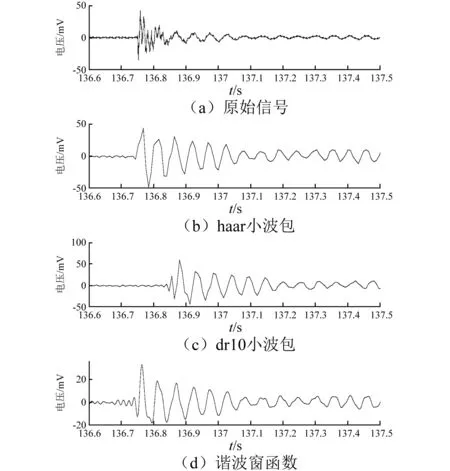
圖7 一階振動信號分解重構后時域圖Fig.7 The first order vibration signal decompositionand reconstruction in time domain

(3)由(a)圖可以看到，在梁受到激勵后，信號波形中首先出現的是波谷，(b)、(c)圖的波形中首先出現的均為波峰，而(d)圖中很好的提取到了波谷信息；(d)圖中的波形與(b)、(c)圖相比更加平滑。其原因在于，傳統小波包分解為了便于計算機進行編碼與壓縮，其變換過程實質上為隔點采樣過程。當振動信號出現在兩次采樣之間時容易導致有用信息的漏采；同時，由于數據量有所減少，所以信號失真程度也必然有所增大。雖然，小波工具箱提供的重構函數通過插值較好的改善了這一問題，但重構信號與真實信號仍然有一定差異。諧波窗函數法在分解與重構的整個計算過程中均對所有數據統一運算，有效避免了振動信號的遺漏。說明諧波窗函數法分解重構后的結果失真更小。

(4)(c)圖與(b)圖相比，在振幅最大的波峰前多了一個小的波峰，且整個波形存在一定差異，其中波峰與波谷處最為明顯。其原因主要在于小波母函數的選取不同。說明選擇不同的小波母函數將導致分解結果的不一致，為后期分析結果的準確性帶來影響。

(5) (a)圖與(d)中波形起振點出現在136.75 s，(b)圖出現在136.73 s，(c)圖出現在136.85 s。結果表明，傳統小波包變換分解后的信號出現了相移，其中“db10”小波的分解結果相移最為明顯。說明傳統小波包分解法易帶來信號的相移，且相移程度與小波母函數的選取有關，而諧波窗函數法實現了很好的鎖相功能。

3.3 基于諧波窗函數的5階振動信號分解與重構

由圖6中(b)圖可以發現，在0～62.5 Hz頻段仍然包含有大量噪聲，特別是50 Hz處有一明顯噪聲，而且在整個頻段內存在大量的50 Hz的倍頻干擾噪聲。所以，圖7中(d)圖的波形中仍然存在一些小的畸變。根據表1中最后一列的頻段范圍確定窗口大小，構建諧波窗函數(由于各階次信號對應的分解頻段均不從0 Hz開始，故此時諧波窗函數變為[0 1 0 1 0]型)。采用諧波窗函數法，按照3.2節中分解重構步驟對5階振動信號再次進行分解與重構。其結果如圖8、圖9所示。

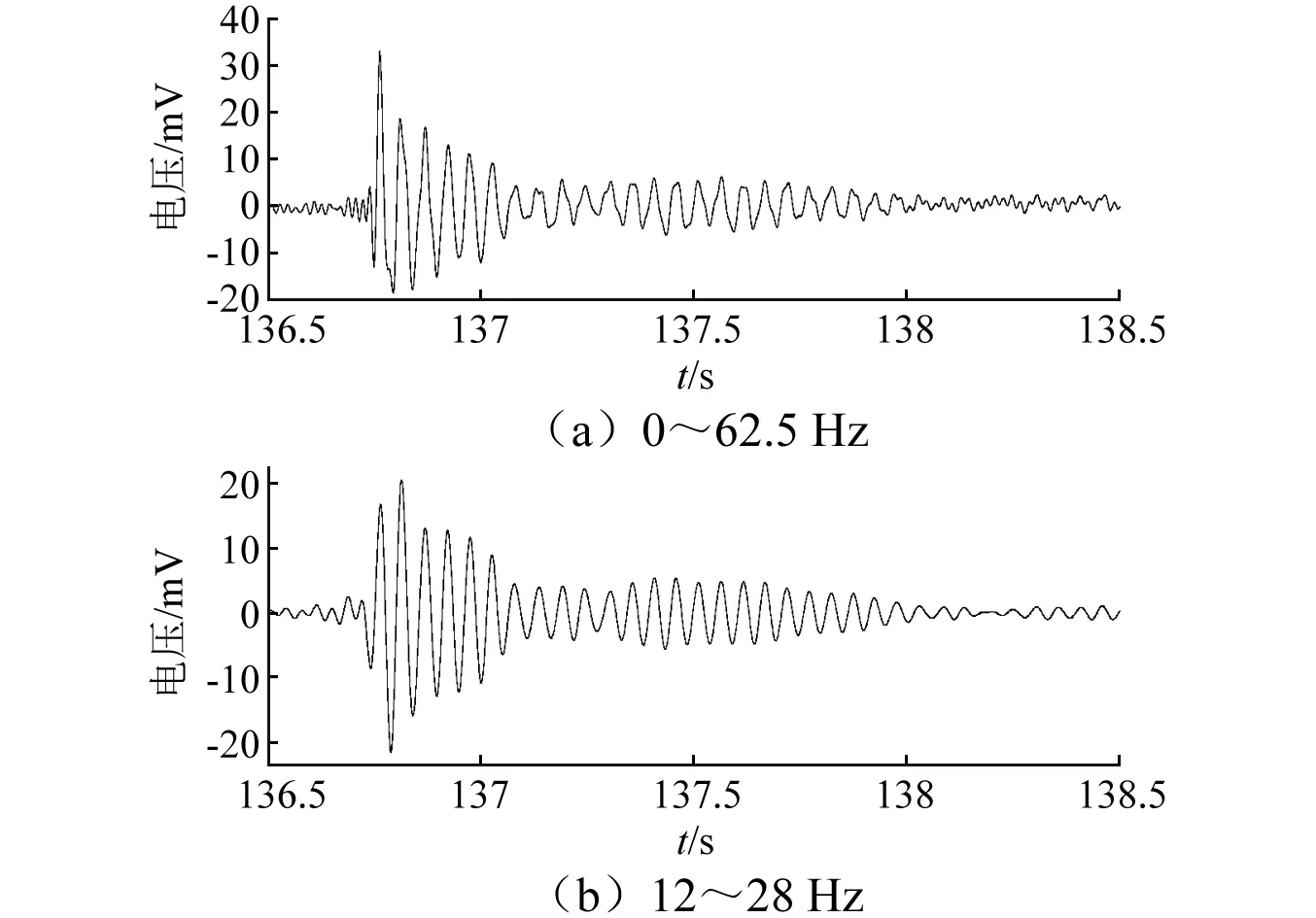
圖8 一階振動信號對比圖Fig.8 Comparison of first order vibration signals

圖8為一階振動信號分別在0～62.5 Hz與12～28 Hz范圍內分解重構的時域信號對比圖，其中(a)圖與圖7中(d)圖相同。(a)圖中，首個波峰的幅值超過33 mV，隨后波峰從19 mV開始依次衰減；波谷最小值為-19 mV，隨后依次衰減，波峰與波谷的包絡出現了一定的“不對稱”現象；波峰與波谷附近的波形出現了畸變。(b)圖中，首個波峰幅值下降為16 mV，第二個波峰為19 mV，波谷最小值為-21 mV，波峰與波谷的包絡表現出一定的“對稱”性；各波峰與波谷波形的畸變現象消失，波形更加平滑。假設被濾除信號均為噪聲信號，對比兩圖中信號的信噪比，可以發現信噪比提升了22%

說明諧波窗函數法可以通過限定更窄的頻帶寬度，實現分析頻段的準確定位，提高分解重構后信號的質量；在信號分解過程中濾除了更多的噪聲信號(特別是50 Hz噪聲)，省去了信號分析前對信號進行濾波預處理的工序，提高了分析效率；同時，由于濾波功能的實現，使得信號失真程度進一步降低，信噪比得到了提升。

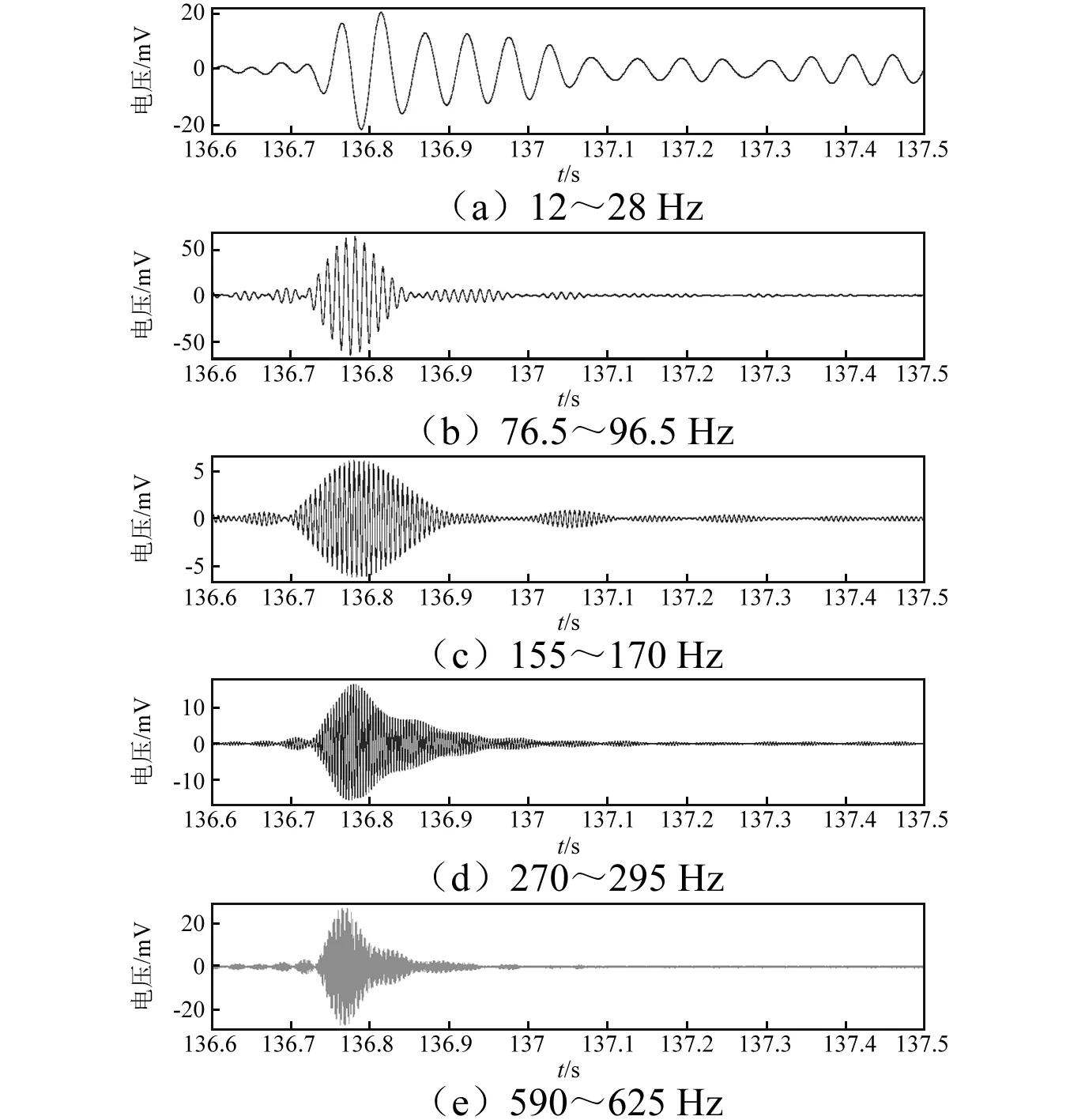
圖9 五階振動信號提取結果Fig.9 Five order Extracted signals

圖9為5階信號分解重構后的時域信號。從圖中可以看出，各階信號均成功的從原始信號被提取出來，且失真小、無相移。為后續的損傷檢測分析提供了高質量的基礎數據。

4 結 論

文本利用基于小波變換思想構建的諧波窗函數成功實現了對信號的分解與重構。通過對一鋼筋混凝土梁實測振動信號的分析，得出以下結論：

(1)諧波窗函數法可以實現分析頻段的自由劃分，并提取出相應頻段的信號。

(2)與傳統小波變換相比，采用諧波窗函數法提取出的信號無數據量的損失，信號波形更加平滑，同時避免了因小波母函數選取不當帶來的信號失真。

(3)由于諧波窗函數具有良好的“盒形”頻譜，所以提取后信號無相移，表現出良好的鎖相效果。

(4)在分解過程中，通過選擇恰當的解頻段，可以在提取信號的同時實現噪聲的過濾。