地磁輔助信息的旋轉彈姿態估計方法*

龍達峰,孫俊麗,溫晶晶

(1 惠州學院,廣東惠州 516007;2 中北大學信息與通信工程學院,太原 030051;3 晉西工業集團有限責任公司,太原 030027)

0 引言

由于旋轉彈發射高過載、高速旋轉和彈載空間狹小等惡劣彈載環境的限制,適用于旋轉彈用的測量傳感器主要有MEMS陀螺儀、地磁傳感器和GPS等[1-4],而且現有導彈彈載姿態測量系統直接移植于高速旋轉彈導航應用時會出現各種問題。特別是彈丸發射時高達10 000g的極大過載,使得彈載姿態測量傳感器容易出現短時的飽和失真、性能退化、甚至失效等,造成彈載測量系統的性能嚴重退化、參數不全或是導航初始參數獲取困難等問題[5]。針對彈載姿態測量系統移植應用問題,目前普遍采用對彈體本身進行局部改造以實現測量系統的移植應用,但這些改造方會影響到依靠旋轉穩定工作方式彈丸的氣動力特性,且造成彈載裝置結構變得非常復雜,從而極大地增加了旋轉彈智能化改造難度[6]。因此,研制具有易移植、小體積和高精度的旋轉彈用姿態測量系統成為其制導化改造的難點所在。此外,在彈載慣導測量系統中,若對低精度MEMS陀螺測量輸出角速率的積分解算存在嚴重的誤差累積。考慮到基于地磁信息的磁測姿態系統是通過測量彈體內地磁場矢量信息來確定彈體姿態方法,其測量誤差不隨時間累積[7-8]。因此,文中提出了一種利用地磁傳感器測量信息對慣性測量系統進行組合濾波方法,由地磁傳感器、MEMS陀螺和GPS測量彈體姿態信息,再根據所建立的組合濾波模型,由改進EKF濾波算法完成旋轉彈飛行姿態準確估計。

1 旋轉彈飛行姿態測量方案

旋轉彈姿態傳感器方案包括三軸地磁傳感器和三軸MEMS陀螺儀,分別用于測量地磁信息和彈體角速率信息。文中選取地面發射坐標系作為導航參考坐標系,因此彈體磁測姿態解算公式為:

(1)

通過對組合濾波模型的可觀測性研究分析發現[9-10],若僅僅利用MEMS陀螺輸出角速率和地磁傳感器輸出信息進行彈體姿態濾波估計,3個姿態角是不完全可觀測的,解決的方法是借助于其它輔助測量方法獲得其中任一個姿態角后再進行組合濾波。考慮到旋轉彈外彈道飛行的特殊性,即便是彈丸受控飛行期間,彈丸飛行也是小攻角狀態,因此在不考慮彈丸的攻角情況下,完全可以利用GPS所測量的彈體速度信息來估算彈體的偏航角和俯仰角,用于代替偏航角不變假設,其估算原理如圖1所示。

圖1 彈丸偏航角和俯仰角估算原理

由圖1所示速度投影關系可知,利用GPS測量所得的速度信息來估算彈體偏航角ψm和俯仰角θm姿態公式為:

(2)

式(2)是假設攻角為零的情況下才能完全成立。然而,若旋轉彈飛行時攻角較小情況下,仍然可以利用式(2)進行計算,所估算所得偏航角和俯仰角會將存在一定的誤差,但其可以當作是測量噪聲帶來的誤差來進行處理,可以通過后續的姿態濾波算法對其進行誤差參數估計與數據補償。

綜合上述測量方案,文中采用以磁測信息、彈體速度估算所得偏航角和俯仰角共同作為系統觀測信息,對慣性導航系統進行姿態組合濾波估計,最終實現旋轉彈飛行姿態的準確測量。

2 旋轉彈彈體姿態估計算法

2.1 彈體姿態組合濾波器結構器設計

為了提高彈體姿態算法的實時性,彈體姿態濾波器采用圖2所示3個濾波器組成的多速率組合式實時濾波結構。其中磁傳感器濾波器和陀螺濾波器分別用于完成彈載地磁傳感器和MEMS陀螺角速率測量輸出的數據的濾波與誤差補償;旋轉彈飛行姿態估計濾波器用于實現彈體偏航角、俯仰角和滾轉角三維姿態角的快速濾波估計。

圖2 多速率組合式的實時濾波器方案

2.2 地磁傳感器誤差估計與補償

彈載地磁傳感器用于測量彈體系坐標內的地磁信息,其測量誤差主要有零偏、靈敏度誤差和交叉耦合誤差等[11-12]。因此,采用公式(3)所示的磁傳感器誤差模型進行地磁傳感器測量誤差參數在線估計和磁測數據補償。

(3)

對測量誤差模型(3)進行進一步的變換,可推導得到三軸磁傳感器測量數據的補償公式為:

(4)

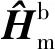
2.3 旋轉彈彈體姿態估計濾波器

由捷聯慣導原理可知,彈體飛行姿態歐拉方程式為[13-14]:

(5)

選取彈體偏航角、俯仰角和滾轉角作為系統的狀態變量Xa=[ψ,θ,γ]T;以彈體飛行姿態歐拉方程式(5)作為狀態方程,將其可簡寫為如下一般形式:

(6)

v(t)

(7)

式中,ci,si(i=ψ,θ,γ)分別為余弦函數cosi和正弦函數sini的簡寫形式。由于上述觀測方程是非線性方程,將其簡寫為如下形式:

Za(t)=h[Xa(t),t]+v(t)

(8)

因此,由狀態方程(5)和觀測方程(7)共同構成彈體姿態組合濾波模型。

2.4 改進EKF的彈體姿態濾波算法

考慮到上述所構建的姿態組合濾波模型是強非線性特征,濾波模型的線性與離散化處理時,傳統EKF濾波算法實質上是基于一階近似的線性化方法,在Taylor級數展開關系式中并沒有取其余高階項,只取一階項,分析發現其會帶來較大的系統誤差,使得其濾波估計精度有所下降。因此,文中在進行模型的離散化及線性處理時,采用二階近似方法來降低線性化帶來的系統誤差,即取到Taylor級數展開的二階項,通過這樣的方法以降低線性化帶來的系統誤差,為進一步提高EKF算法精度。相比于線性一階逼近的EKF濾波算法,文中所采用基于二階近似的改進EKF濾波算法主要不同在于如下兩個方程:

(9)

式中：ei為第i個標準基向量,即第i個元素為1,其余為0;tr(·)表示取矩陣的跡,也即為取矩陣主對角元素之和;Hx為觀測方程的雅可比矩陣;而Hxx,i為觀測方程Hessian矩陣,其計算公式為:

(10)

算法除上述公式不同,二階近似改進EKF濾波算法與傳統EKF濾波算法基本相同,其主要流程也包括初值選取、狀態預測與量測更新3個濾波算法步驟,但由于進行Taylor展開時取二階近似,所以狀態預測和量測更新方程有所不同。因此,基于二階近似改進EKF濾波算法具體步驟如下:

1)濾波初始參數:

2)時間更新過程:

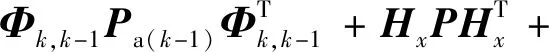
3)量測更新過程:

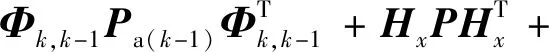
因此,通過上述的初值選取、狀態預測與量測更新3個濾波算法步驟,最終完成彈載飛行姿態參數的快速濾波估計。

3 算法的仿真驗證

3.1 仿真參數設置

文中選取152 mm高速旋轉彈為仿真對象,根據旋轉彈外彈道數學模型,首先利用Matlab程序計算機仿真生成外彈道飛行數據以及各彈載姿態傳感器測量輸出的理想數據。然后,再根據所建立的彈載傳感器的測量誤差模型,并按如表1所示的彈載傳感器誤差參數設置,仿真生成彈載傳感器的實際測量輸出數據,在此基礎上進行彈體飛行姿態估計算法的仿真驗證。

表1 彈載傳感器誤差參數設置

3.2 數值仿真及結果分析

根據上述仿真設置的條件,旋轉彈外彈道飛行軌跡如圖3所示。

圖3 彈丸外彈道曲線

采用前述基于改進EKF的彈體姿態濾波算法完成旋轉彈飛行偏航角、俯仰角和滾轉角三維姿態的濾波估計,彈體姿態濾波估計結果如圖4～圖9所示。

圖4 偏航角濾波估計結果

圖5 俯仰角濾波估計結果

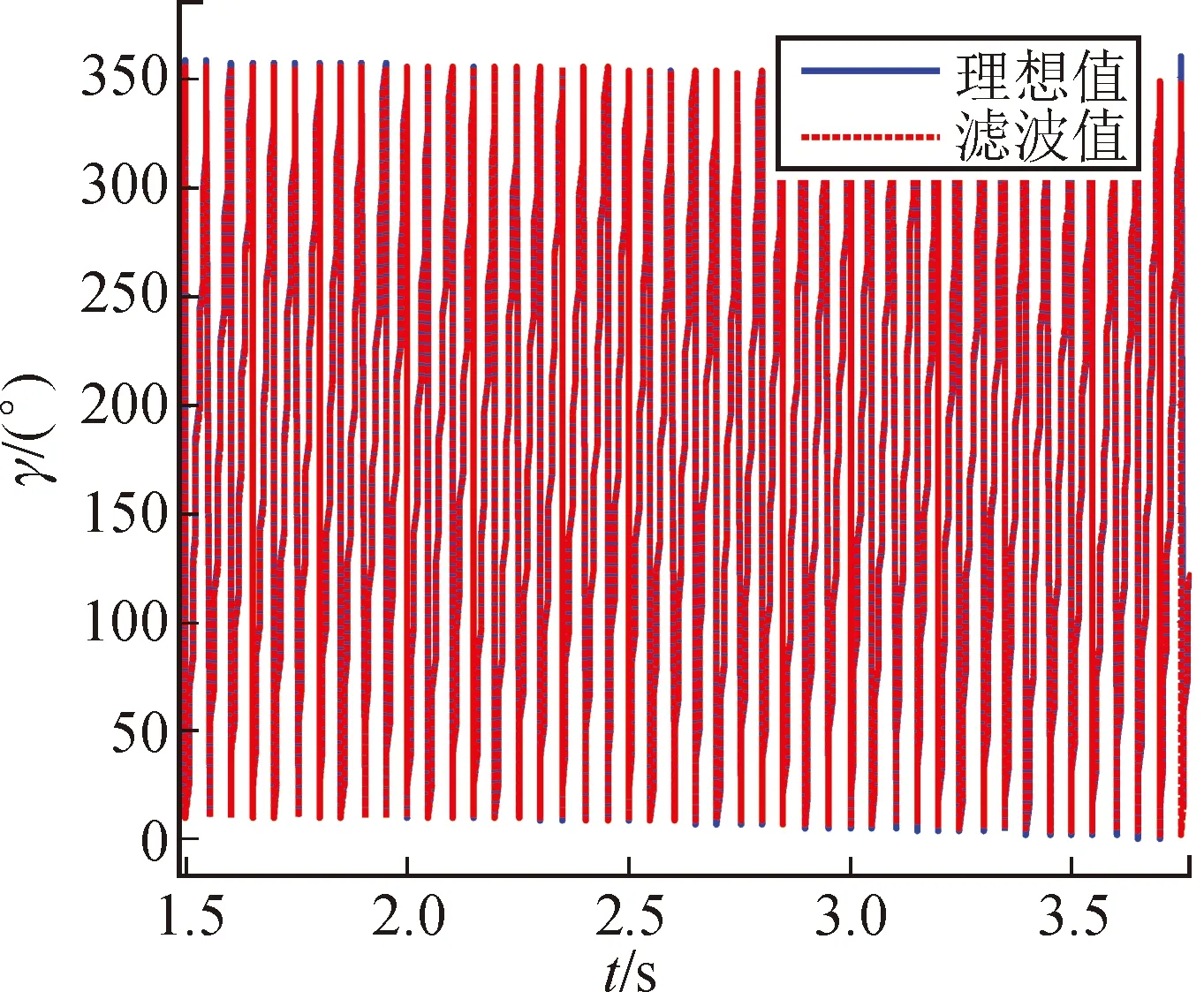
圖6 滾轉角濾波估計結果

圖8 俯仰角估計誤差曲線

圖4～圖6所示分別為彈體偏航角、俯仰角和滾轉角的理論值與濾波估計值的結果對比,圖中藍色實線為旋轉彈理想彈道條件下的彈體姿態角,而紅色虛線所示為彈體姿態算法濾波估計所得三維姿態角,與之相對應的彈體偏航角、俯仰角和滾轉角姿態角估計誤差如圖7～圖9所示。

圖9 滾轉角估計誤差曲線

從上述姿態估計結果來看,其彈體三維姿態在5 s內基本能夠得到很好的收斂,在濾波穩定后,經統計得彈體偏航角、俯仰角和滾轉角姿態估計誤差分別為0.806 8°、0.839 2°和3.926 4°(1σ估計誤差),結果表明彈體姿態濾波算法可以快速完成彈體飛行姿態準確估計。

4 結論

針對旋轉彈飛行姿態測量問題,文中采用地磁傳感器、MEMS陀螺和GPS姿態組合測量方案,建立了基于多速率組合式彈體姿態濾波模型,并采用了基于改進EKF的彈體姿態濾波算法完成彈體的姿態估計方法。最后選取152 mm旋轉彈為研究仿真對象,利用計算機仿真方法進行了所述算法的仿真驗證。仿真結果表明,彈體三維姿態在5 s內能夠實現很好的收斂,在濾波穩定后,彈體三維姿態在5 s內能夠得到很好的收斂,經統計得彈體偏航角、俯仰角和滾轉角3個姿態角估計誤差分別為0.806 8°、0.839 2°和3.926 4°,驗證了文中所述算法可以快速完成彈體飛行姿態準確估計。