基于最小二乘法的彈體參數辨識工程算法*

楊云剛,趙軍民,劉鈞圣,王 琨,王 剛,王齊雙

(西安現代控制技術研究所,西安 710065)

0 引言

精確的導彈彈體參數是導彈總體方案設計與優化、飛行性能分析、控制系統設計及飛行試驗方案制定的重要前提和基礎。工程研制過程中,通常采用理論計算[1]、風洞試驗[2]和發動機地面點火試驗等方法獲取導彈的氣動參數和推力參數,但由于理論模型的差異、風洞洞壁干擾、發動機推力臺測量誤差等局限性,造成飛行試驗的結果往往與理論值存在或大或小的差異[3-4]。此外,隨導彈研制工作的進展,一般會對導彈結構、氣動布局進行優化改進,必然帶來彈體參數的改變,而頻繁進行費用昂貴的風洞試驗并不現實。針對這一問題,參數辨識算法應運而生并得到大力發展。

在參數辨識領域中,最小二乘法是一種得到最廣泛應用的估計方法,可用于動態、靜態、線性、非線性系統[5-7]。但在工程實踐中,一方面,導彈通常經歷大推力增速、小推力續航、無動力滑行等階段,采用傳統最小二乘法對整個飛行過程建立的系統辨識方程會出現嚴重病態,進而得出誤差較大甚至錯誤的結果,對導彈總體設計與工程實踐缺乏指導意義;另一方面,無論氣動力線性模型還是非線性模型[8],均與導彈風洞試驗的氣動參數存在一定誤差,引用參數辨識方法對氣動力數學模型進行辨識并不具有直接的工程使用價值。

文中以某型紅外圖像制導空地導彈為研究背景,提出一種基于最小二乘法的彈體參數辨識工程算法,在發動機地面點火試驗推力數據和導彈風洞試驗氣動數據基礎上,設計了推力修正系數和阻力修正系數,并針對導彈發射增速段、續航飛行段和無動力滑行段分別建立最小二乘法彈體參數辨識模型。該方法能有效解決辨識方程病態問題,易于工程實現,已在導彈型號研制中得到成功應用。

1 彈體參數辨識工程算法建模

1.1 最小二乘法原理

設觀測方程為：

y=Cλ+ε

(1)

式中:y為觀測矢量;C為參數靈敏度系數矩陣;λ為待辨識參數;ε為測量噪聲,并設測量噪聲為等方差白噪聲。

(2)

容易證明,最小二乘法的估計值是無偏的。

1.2 系統彈體參數辨識模型

導彈飛行過程一般由發射增速段、續航飛行段和無動力滑行段組成,可利用彈上慣導進行導彈飛行過載、速度、姿態角及姿態角速度的測量。導彈速度方案主要受發動機推力和氣動阻力影響,其他因素影響較小,易于彈體參數辨識,因此選取導彈軸向過載為觀測量,結合導彈飛行力學原理,系統觀測方程為:

kpPicosαcosβ-kcxcxiqS=mgnx2

(3)

為解決信息矩陣病態問題,有學者提出貝葉斯法、嶺估計法等有偏估計方法,但這些方法依賴于驗前信息的準確性或受損失函數的合理性,但若驗前信息不可信,反而導致參數辨識結果不正確。針對該問題,文中對導彈飛行過程劃分為發射增速段、續航飛行段和無動力滑行段,各階段分別建立彈體參數辨識模型,從而有效解決了信息矩陣病態問題,非常易于工程實現。

1.3 發射增速段參數辨識模型

發射增速段發動機推力遠遠大于氣動力,因此將方程(3)簡化為:

kpPicosαcosβ=mgnx2

(4)

選取Picosαcosβ為參數靈敏度系數矩陣,根據最小二乘法原理,發射增速段參數辨識模型為:

kp(i)=([Picosαcosβ]T[Picosαcosβ])-1·

[Picosαcosβ]Tmgnx2(i),kp(0)=kp0

kcx(i)=kcx(i-1),kcx(0)=kcx0,i=1,2,3,…

(5)

式中:kp0為發動機推力修正系數初值;kcx0為阻力修正系數初值。

1.4 續航飛行段參數辨識模型

一般續航飛行段發動機推力與氣動阻力量值相當,因此以方程(3)為觀測方程,參數靈敏度系數矩陣為:C1=[Picosαcosβ-cxiqS],根據最小二乘法原理,續航飛行段參數辨識模型為:

(6)

1.5 無動力滑行段參數辨識模型

無動力滑行段發動機推力為0,導彈速度主要受氣動阻力影響,因此將方程(3)簡化為:

-kcxcxiqS=mgnx2

(7)

選取-cxiqS為參數靈敏度系數矩陣,根據最小二乘法原理,無動力滑行段參數辨識模型為:

(8)

2 數字仿真及分析

2.1 試驗數據預處理

飛行試驗環境的復雜性、數據采集系統的非理想性等眾多因素,不可避免地使飛行試驗實測數據帶有誤差和噪聲,這些誤差可能導致參數辨識過程發散,甚至收斂到錯誤結果[9],因此在參數辨識之前,必須對飛行試驗實測數據進行預處理,降低實測數據中的各種噪聲和系統誤差,以提高彈體參數辨識的準確度。

文中對飛行試驗獲得的實測數據進行5點平滑濾波處理。需要預處理的數據包括3個姿態角(俯仰角?、偏航角ψ、滾轉角γ)、彈體系3個方向過載(X向過載nx1、Y向過載ny1、Z向過載nz1)、發射系3個方向速度(Vx,Vy,Vz),處理方法為:

(9)

式中:x為原始測量數據;yo為處理后數據。

2.2 中間參數計算

根據關系式(10),由預處理后的Vx,Vy,Vz,計算可得彈道傾角θ和彈道偏角ψv;由預處理后的俯仰角?、偏航角ψ、滾轉角γ,經幾何關系方程(11)解算,得到攻角α、側滑角β和速度傾斜角γv;根據關系式(12),對預處理后的彈體系X向過載nx1、Y向過載ny1、Z向過載nz1進行坐標變換,得到彈道系X向過載nx2、Y向過載ny2、Z向過載nz2。

(10)

(11)

(12)

2.3 流程設計

文中彈體參數辨識工程算法流程設計如圖1所示。

圖1 彈體參數辨識工程算法流程設計

2.4 仿真分析

選取某次飛行試驗的實測數據為觀測量,以發動機地面點火試驗推力數據和導彈風洞試驗氣動數據為參考,采用文中基于最小二乘法的彈體參數辨識工程算法進行發動機推力修正系數和阻力修正系數辨識,仿真輸入見表1,彈體參數辨識結果見表2。

表1 仿真輸入

表2 彈體參數辨識結果

圖2 速度曲線對比

由表2結果可知,導彈飛行各階段推力修正系數、阻力修正系數收斂值一致。進一步,為驗證彈體參數辨識結果的正確性,利用表2辨識結果對導彈基準彈體參數修正,進行六自由度彈道仿真計算,仿真結果見圖2～圖6。對比仿真結果和導彈飛行試驗數據,導彈飛行各階段速度、姿態曲線基本重合,表明彈體參數辨識結果與實際相符,即文中彈體參數辨識算法合理有效。

圖3 發射增速段速度曲線對比

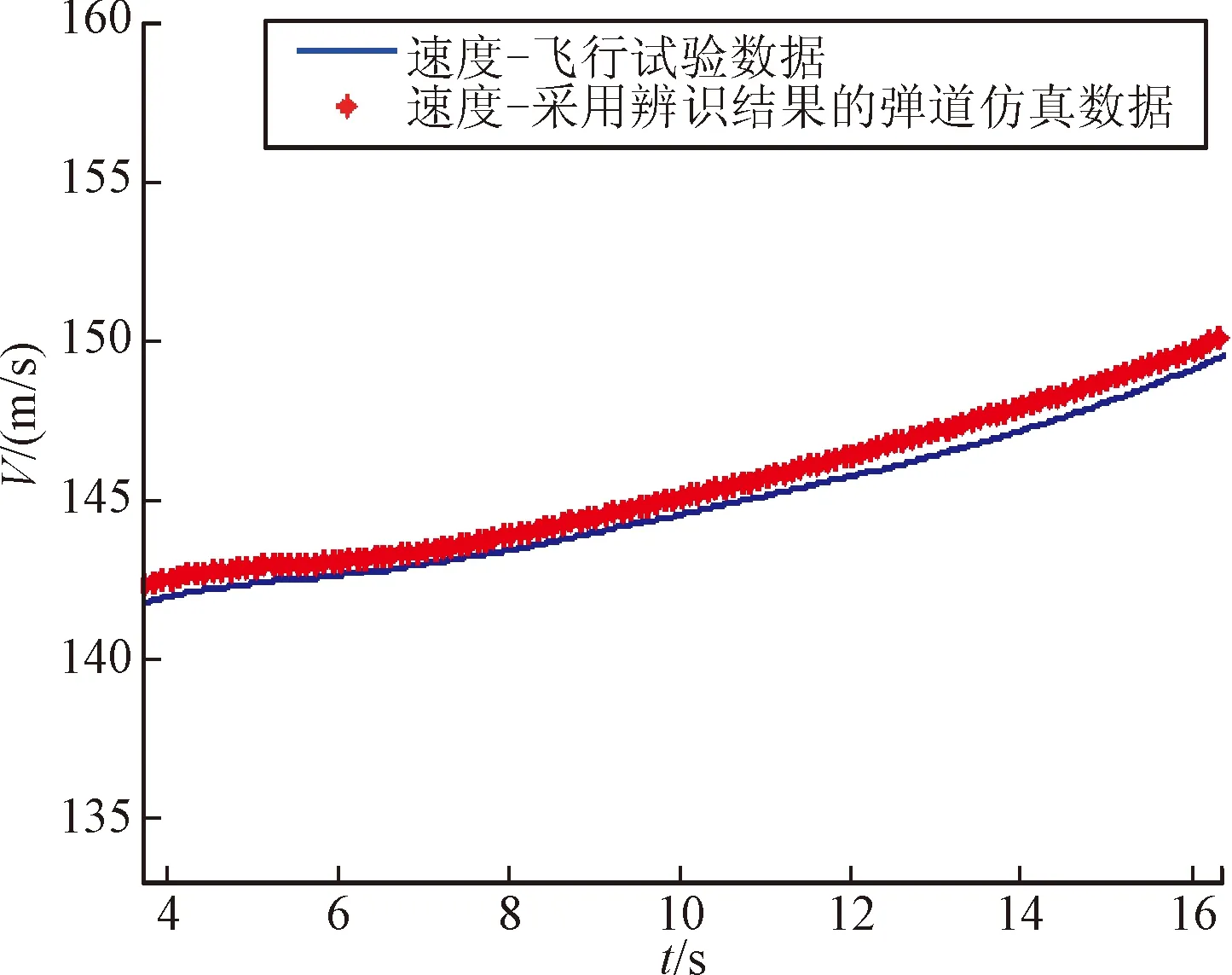
圖4 續航飛行段速度曲線對比

圖5 無動力滑行段速度曲線對比

3 結論

文中以導彈軸向過載為觀測量,以發動機推力修正系數和阻力修正系數為目標,基于最小二乘法對導彈發射增速段、續航飛行段和無動力滑行段分別建立了彈體參數辨識模型,有效解決了傳統最小二乘法辨識方程病態問題,仿真結果驗證了該算法的有效性和準確性。文中提出的彈體參數辨識工程算法以發動機地面點火試驗推力數據和導彈風洞試驗氣動數據為基礎,避免了氣動力建模方法帶來的辨識誤差,非常適用于導彈實際工程研制,已在某型紅外圖像制導空地導彈項目中得到成功應用。特別的,當導彈飛行過程不包含續航飛行段或無動力滑行段時,該算法依然有效。

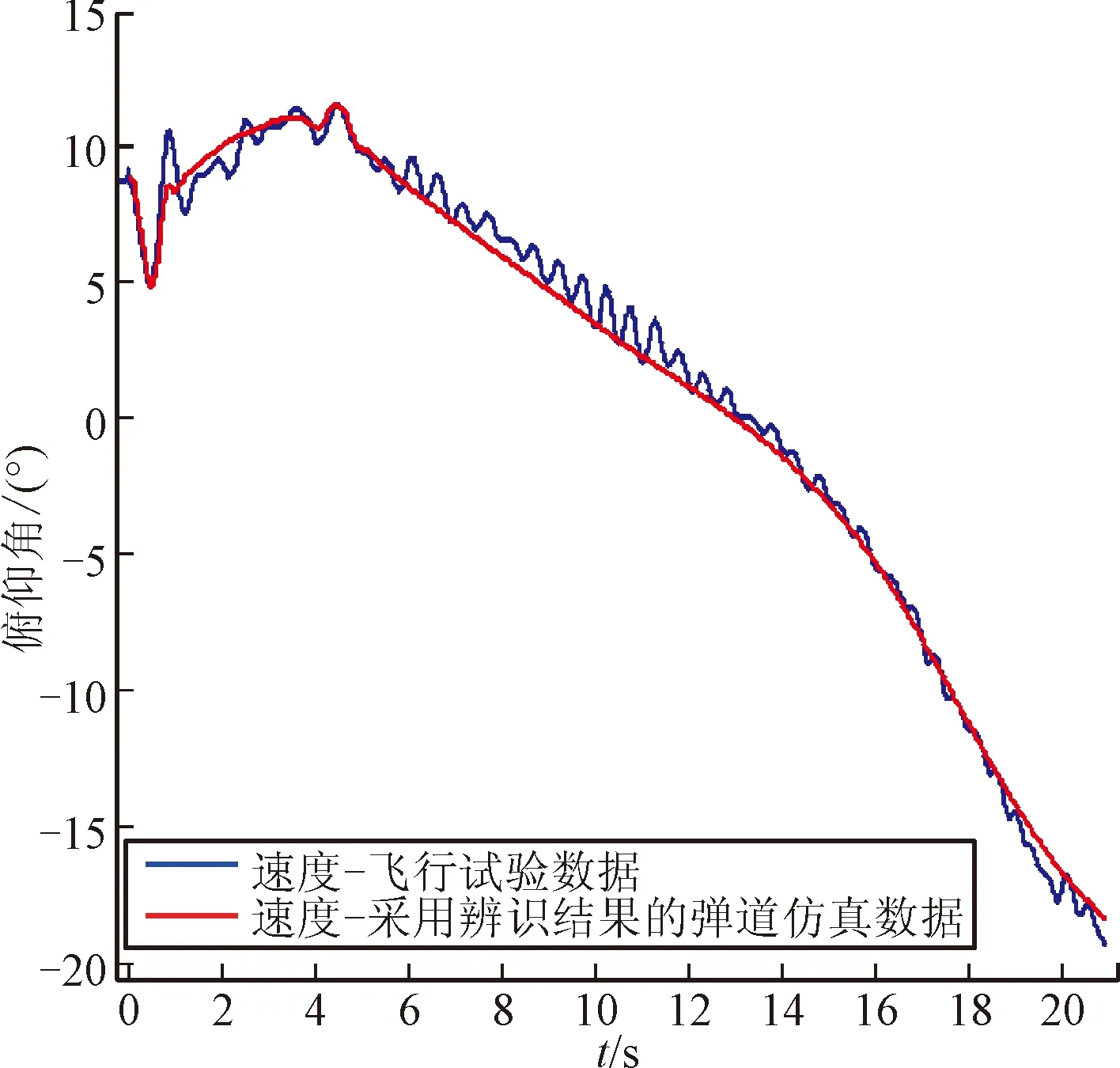
圖6 俯仰角曲線對比