例談數(shù)學(xué)習(xí)題設(shè)計(jì)如何做到“小題大做”

林庚祿

數(shù)學(xué)習(xí)題是課堂教學(xué)的延伸和拓展，習(xí)題不但是教師檢驗(yàn)和評(píng)價(jià)課堂效果的方式，更重要的是學(xué)生通過(guò)習(xí)題的練習(xí)可以鞏固和內(nèi)化新知。好的習(xí)題可以使課堂教學(xué)事半功倍，有利于學(xué)生新知的掌握，促進(jìn)思維的發(fā)展；不好的習(xí)題，將是枯燥無(wú)味的機(jī)械重復(fù)，自然事倍功半，抑制了學(xué)生學(xué)習(xí)的積極性。所以，我們?cè)谠O(shè)計(jì)習(xí)題時(shí)，應(yīng)做到難易適中，明確設(shè)計(jì)意圖，真正做到“小題大做”，使習(xí)題作用最大化，更好地服務(wù)于學(xué)生的學(xué)習(xí)。

一、突破思維定勢(shì)，學(xué)會(huì)逆向思考

平常習(xí)題的呈現(xiàn)方式，都是以圖文或純文字的形式出現(xiàn)，即出示已知條件與問(wèn)題，要求學(xué)生列式解答。教學(xué)時(shí)發(fā)現(xiàn)，如果打破常規(guī)，先有列式，再要求說(shuō)明列式表示的意義時(shí)，學(xué)生普遍感覺(jué)不習(xí)慣，有的甚至束手無(wú)策。

例如：學(xué)校口琴興趣小組有男生20人，女生有15人，根據(jù)列式（20-15）÷20，寫(xiě)出它表示什么意義。看似簡(jiǎn)單一道題，學(xué)生也犯難，這是定勢(shì)思維對(duì)學(xué)習(xí)的影響。正是由于小學(xué)生習(xí)慣了先有問(wèn)題，再有列式的解題方式，形成了一定的思維定勢(shì)，所以我們要突破這種思維定勢(shì)，多設(shè)計(jì)一些先有列式，再要求說(shuō)明表示意義的習(xí)題。這種從列式入手說(shuō)意義的習(xí)題，有利于學(xué)生理清數(shù)量關(guān)系，內(nèi)化解決實(shí)際問(wèn)題的方法，同時(shí)達(dá)到訓(xùn)練學(xué)生逆向思維與融會(huì)貫通的能力，提高解決問(wèn)題的能力。

當(dāng)然也可以設(shè)計(jì)根據(jù)算式補(bǔ)充適當(dāng)?shù)臈l件或問(wèn)題的習(xí)題。

又如：小軍有郵票36枚，小軍的郵票比小明多，______________？

以上練習(xí)都可以從不同的角度促進(jìn)學(xué)生思維的發(fā)展，使分?jǐn)?shù)問(wèn)題的解決方法得到內(nèi)化，并形成解決問(wèn)題的數(shù)學(xué)模型，且應(yīng)用于實(shí)際解決問(wèn)題中。

當(dāng)然，也可以根據(jù)列式讓學(xué)生編題。例如：根據(jù)列式 120×（1+）、120×（1－）等編寫(xiě)出相關(guān)分?jǐn)?shù)實(shí)際問(wèn)題，促進(jìn)學(xué)生知識(shí)的內(nèi)化。讓學(xué)生看著列式編題目，賦予枯燥的算式具體、生動(dòng)的情境，讓學(xué)生在編題目中進(jìn)一步明晰算理，讓計(jì)算不再是為算而算，在堅(jiān)守“數(shù)學(xué)味”的同時(shí)，給予學(xué)生個(gè)性發(fā)揮想象的空間，使他們體會(huì)到呆板的算式背后的豐富內(nèi)涵和魅力。

二、注重新舊聯(lián)系，促進(jìn)形成知識(shí)體系

建構(gòu)主義學(xué)習(xí)理論指出：有效的數(shù)學(xué)學(xué)習(xí)應(yīng)是聯(lián)通各知識(shí)之間的關(guān)系，正確把握知識(shí)之間的因果關(guān)系，將有聯(lián)系的或?qū)⑼活?lèi)的知識(shí)點(diǎn)組成一個(gè)模塊，建立整體認(rèn)識(shí)，形成一定的完整知識(shí)體系。

例如：在學(xué)習(xí)多邊形面積計(jì)算時(shí)，可以設(shè)計(jì)以下習(xí)題。

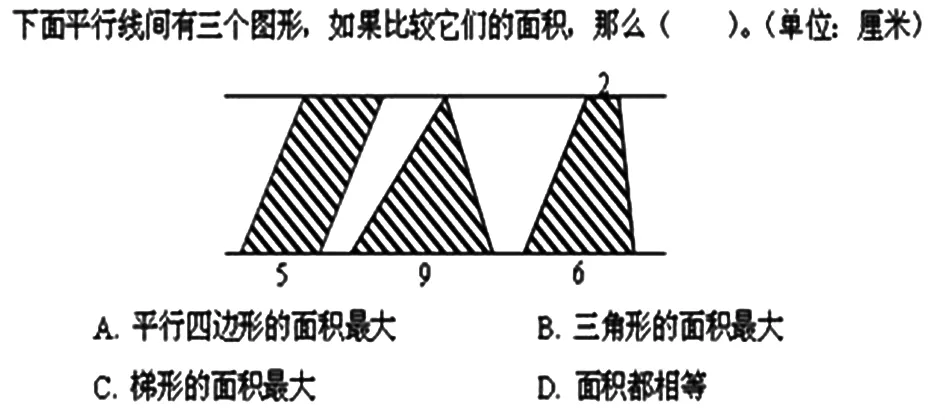
該習(xí)題把三種多邊形編排在一起，激發(fā)學(xué)生回顧與反思三種圖形面積公式的推導(dǎo)過(guò)程，明白三種圖形的面積推導(dǎo)都是利用轉(zhuǎn)化的數(shù)學(xué)思想方法，將舊知識(shí)轉(zhuǎn)化為新知識(shí)得到的，較好地將平行四邊形、三角形和梯形等面積計(jì)算方法產(chǎn)生聯(lián)系。該習(xí)題要求學(xué)生明確：決定多邊形面積大小的因素，包括底和高。學(xué)生通過(guò)觀察題干，發(fā)現(xiàn)三個(gè)圖形都在同一組平行線間，說(shuō)明了它們的高相等，要比較三者的面積就只要考慮它們的底即可。再由于三角形和梯形的面積都需要底乘高除以2，只有平行四邊形的面積不需要除以2，很容易就判斷出平行四邊形的面積最大。通過(guò)該練習(xí)題讓學(xué)生感受到在沒(méi)有完整告知每一個(gè)圖形的具體長(zhǎng)度情況下，也照樣能比較出不同圖形面積的大小。這樣的習(xí)題練習(xí)既鞏固了多邊形面積的計(jì)算方法，又理清了圖形面積計(jì)算的差異，使得學(xué)生對(duì)數(shù)學(xué)知識(shí)有進(jìn)一步深刻的理解，并逐漸建立多邊形面積計(jì)算的整體認(rèn)識(shí)，形成一定的完整知識(shí)體系。

三、注重說(shuō)理，展露思維過(guò)程

《數(shù)學(xué)課程標(biāo)準(zhǔn)（2011版）》指出：評(píng)價(jià)不僅要關(guān)注學(xué)生的學(xué)習(xí)結(jié)果，更要關(guān)注學(xué)生在學(xué)習(xí)過(guò)程中的發(fā)展和變化。因此，在習(xí)題的設(shè)計(jì)時(shí)，我們要改變習(xí)題中問(wèn)題的呈現(xiàn)方式，不要一味地只有列式解答和填空，更多一些“寫(xiě)出你的理由”，“請(qǐng)你寫(xiě)出你的思考過(guò)程”等，以此充分展露學(xué)生的思維過(guò)程。

例如：在測(cè)量角的度數(shù)時(shí)，可以設(shè)計(jì)如下圖這類(lèi)習(xí)題：

學(xué)生完成情況：

以上習(xí)題設(shè)計(jì)不再是只讓學(xué)生看圖得到角的度數(shù)，更重要的是，要求學(xué)生寫(xiě)出“我是這樣想的”。通過(guò)讓學(xué)生寫(xiě)理由來(lái)展露學(xué)生的思維過(guò)程，可以幫助學(xué)生進(jìn)一步理清角度量的知識(shí)，促進(jìn)對(duì)知識(shí)本質(zhì)的深刻理解。

又如：學(xué)習(xí)了《乘法結(jié)合律》后，可以設(shè)計(jì)：

a×b×c=a×(b×c)，這是乘法結(jié)合律。那么，在除法中，是否同樣存在 a÷b÷c=a÷ (b÷c)呢？請(qǐng)說(shuō)明你的理由。

再如：學(xué)習(xí)了《分?jǐn)?shù)的基本性質(zhì)》后，可以設(shè)計(jì)：

根據(jù)分?jǐn)?shù)與除法的關(guān)系，你能用除法中商不變的規(guī)律來(lái)說(shuō)明分?jǐn)?shù)的基本性質(zhì)嗎？請(qǐng)舉例說(shuō)明。

學(xué)生要較好地完成每道說(shuō)理題，離不開(kāi)一定的訓(xùn)練。這就要求教師要改變教學(xué)理念，課堂教學(xué)要做到學(xué)習(xí)過(guò)程與學(xué)習(xí)結(jié)果并重，課堂中多問(wèn)幾個(gè)“為什么”“說(shuō)說(shuō)你是怎么想的”等，摒棄教師“一言堂”的教學(xué)方式，提倡尊重平等交流的“對(duì)話”式教育，留給學(xué)生更多課堂“獨(dú)白”的時(shí)間和思維空間，真正做到“知其然而更知其所以然”，最大限度地啟發(fā)學(xué)生的智慧潛能。

習(xí)題是學(xué)生掌握基礎(chǔ)知識(shí)和開(kāi)展技能訓(xùn)練與形成技巧的重要手段,也是積累基本活動(dòng)經(jīng)驗(yàn)和滲透數(shù)學(xué)思想的有效方法。每一道習(xí)題都承載著設(shè)計(jì)者的教學(xué)意圖和思想，要想真正發(fā)揮小習(xí)題、大作用，就需要我們?cè)O(shè)計(jì)者高標(biāo)準(zhǔn)、嚴(yán)要求，設(shè)計(jì)好每一道題目。