對種群數量變化中重要參數λ值的解讀

劉 莉 宋立偉

(黑龍江省大慶實驗中學 163000)

在人教版高中生物學教材必修3第4章中講述了種群數量變化的三種模型，由此引出數學模型的構建方法。“J”型增長的模型假設為：在食物空間條件充裕、氣候適宜、沒有敵害等條件下，種群的數量每年以一定的倍數增長，第二年的數量是第一年的λ倍，所以t年后種群數量Nt=N0λt。由此可以看出，λ值是前后兩段時間之間種群數量的倍數，即λ=Nt/Nt-1。λ值的大小能反應種群數量的變化趨勢，也與種群的增長率有密切關系。

1 λ值與增長率的關系

增長率是指單位數量的個體在單位時間內新增加的個體數，即增長率=新增加個體數/初始數量×100%。通過比較增長率的計算公式和λ值的計算公式可以看出，λ≠增長率。雖然兩者沒有相等的關系，但由以下推導過程可看出兩者關聯。

增長率=新增加個體數/初始數量×100%=(Nt-Nt-1)/Nt-1×100%=(Nt-1λ-Nt-1)/Nt-1×100%=(λ-1)×100%。

2 λ值與種群數量變化的關系

在“J”型增長曲線中，種群數量每年以一定的倍數增長，可知λ是一個不變的數值。因為增長率=λ-1，所以在“J”型增長曲線中，增長率也是固定不變且大于0的數值，同時也說明λ值是一個大于1且不變的數值。

對于“S”型增長曲線，部分學生誤認為其不存在λ，理由是教材中沒有提到λ值的問題。事實上，“S”型增長模型的假設中提到：自然界的資源空間總是有限的，當種群密度不斷增大時，生存斗爭加劇，使種群的出生率不斷下降，死亡率不斷提升，最終種群數量維持在K值左右穩定(在此處教材已經提示了“S”型增長的λ值問題)。由此可知，“S”型增長曲線的增長率是逐漸下降的，直到種群數量達到K值時，種群增長率下降至0。如前所述，增長率=λ-1，即λ=增長率+1，可知“S”型增長曲線的λ>1但不斷下降，當λ=1時，增長率=0，種群數量不變。如λ<1，說明增長率<0，種群數量正在減少。λ值大小與種群數量間的關系如表1所示。

表1 λ值與種群數量變化的關系

例題：在某森林的固定位置和固定時間，用固定數量的鳥籠捕捉的方法，統計大山雀種群數量。在連續10年內得到圖1所示的曲線(圖中λ表示該種群數量是前一年種群數量的倍數)，下列分析正確的是( )

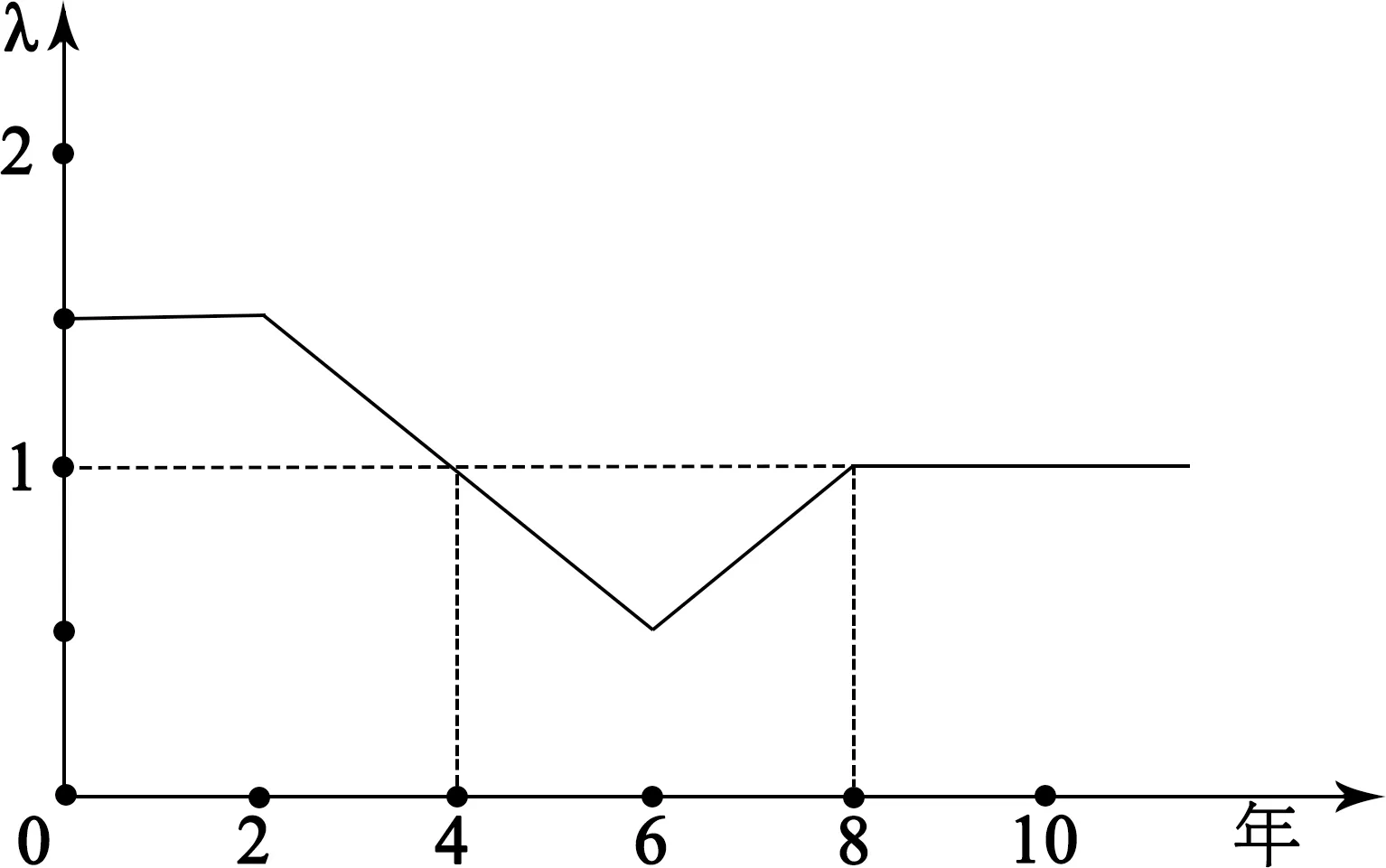
圖1 某森林內大山雀的種群數量

A.因為放置鳥籠的位置固定，此種群數量的調查方法為樣方法

B.0～2年內種群的年齡組成為穩定型

C.種群數量下降是從第4年后開始

D.第4年和第8年種群數量相等

分析：從圖中可以看出，0～2年種群數量呈“J”型增長，2～4年種群數量呈“S”型增長，第4年時種群數量最大(第2至第4年λ值下降，但λ>1，盡管增長率減小，但種群數量還是在增長)。第4至第8年，λ<1，說明種群數量一直下降，第8年時種群數量最小。第8年后，λ=1，種群數量保持不變。因此，參考答案為C。