基于層次分析法的軍用危險品車輛運輸路徑選擇研究

王光輝，陳思楊 （空軍勤務學院，江蘇 徐州 221000）

WANG Guanghui,CHEN Siyang (Air Force Logistics University,Xuzhou 221000,China)

危險品運輸的風險影響因素多，路徑影響區人員受到威脅較大，其運輸風險不容忽視[1]。利用層次分析法對各風險因素進行量化處理，對車輛行進路線進行優化，選取更加快捷、可靠的路徑，也為部隊進行危險品公路運輸提供安全、科學、實用的運輸選線管理模式，具有重要的理論意義和實踐指導意義。

1 層次分析法

層次分析法是一種常用的處理決策問題的實用方法，于20世紀70年代由T.L.Saaty提出，是一種定性和定量相結合的系統、層次化的分析方法。層次分析法的步驟一般為建立層次結構模型、構造各層判斷矩陣、各層次單排序和一致性檢驗。

1.1 建立層次結構模型

層次分析法通過分析復雜問題包含的因素及其相互聯系，將問題分為不同的要素，并將這些要素歸并為不同的層次，進而形成多層次結構。根據先分解后綜合的系統思想，首先要對問題進行層次化處理，并根據問題的性質和所要達到的總目標，將問題分為不同的組成要素，按照要素間的相互關系，進行不同層次的聚集組合，形成一個多層次分析結構模型，最終歸結為最底層（方案、措施、指標等）相對于最高層（總目標）的相對重要度的權值或相對優劣次序的問題。

對于主觀決策，首先要弄清需要解決的問題是什么，并把它作為總目標；然后是最終的選擇對象，即方案；在總目標和方案之間的項目是對方案進行評價時所需要的屬性，即評價標準。應用層次結構模型，首先需要建立評價對象的層次結構模型，將決策問題分解為3個層次：最上層為目標層，中間層為準則層，最下層為方案層。

1.2 構造各層判斷矩陣

基于目標層的總目標需要對準則層的影響因素進行成對的比較評價、列出判斷矩陣。判斷矩陣是表示針對上一層某要素而言，是與它有關聯的各要素之間的相對優越程度。

成對比較是進行每一層次水平的各個要素之間的比較。采用成對比較法是基于層次分析法的先分解后綜合的思想不把所有因素放在一起進行比較，而是將一個決策問題分解為若干個更為簡單的決策問題來解決。

成對比較是基于層次分析法中Saaty給出的9級比例標尺，將決策者的偏好判斷數量化，形成判斷矩陣A，最后運用矩陣理論進行偏好分析，求得層次排序或分層權系數。以aij表示因素uki和ukj的影響之比，則判斷矩陣為：

Saaty等學者用實驗的方法比較了在各種不同標度下人們判斷結果的正確性。結果表明采用9級比例標尺最為合適，即與文字敘述評比相對應的數值尺度表為1、3、5、7、9以及介于其中的折中值2、4、6、8，如表1所示[2]。

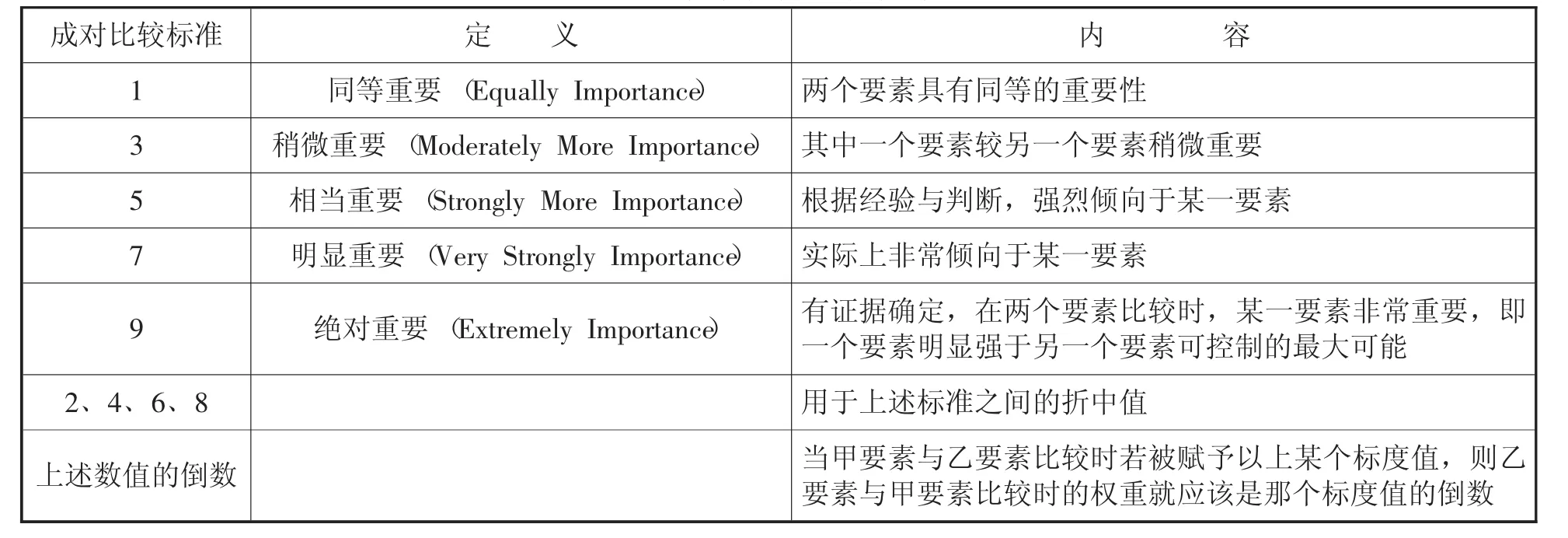
表1 層次分析法評價尺度

1.3 各層次單排序和一致性檢驗

層次單排序即把本層各要素對上一層次排出優劣順序，即求出權重。

在層次分析過程中，判斷矩陣A中的任意一個值aij反映了要素i和要素j之間的重要性之比，它既可以通過這兩個要素間的直接比較而得到，又可以通過其他要素間的兩兩比較而獲得。當決策者的判斷完全一致時，不管用直接方法還是間接方法，要素i和要素j之間重要性的比值都應該是唯一的。但在實際問題的處理過程中，由于判斷對象的復雜性以及人的思維判斷的差異，判斷者對判斷時所采用的標度以及所比較的對象有時缺乏清楚的認識，可能會出現各要素間排序矛盾；或者要素之間經過一系列的一對一比較排序后，其重要性比例缺乏首尾一貫性，即整體排序缺乏滿意一致性。

Saaty引入一致性比例這個一致性評價指標，即：

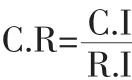
式中：C.R（Consistence Ratio） 為一致性比例，C.I（Consistence Index） 為判斷矩陣的一致性指標，C.I=（λmax-n）/（n-1）；n為判斷矩陣的階數；R.I（Random Consistency Index）為判斷矩陣的隨機一致性指標，其具體數值如表2所示。

表2 隨機一致性指標

若C.R＜0.1，則判斷矩陣具有滿意的一致性；若C.R＞0.1，則判斷矩陣不具有滿意的一致性，需要調整判斷矩陣的值[3]。

2 軍用危險品車輛路徑選取原則

軍用危險品是指用于軍事目的，在運輸過程中容易造成人身傷亡和財產毀損事故的貨物，包括爆炸品、毒害品、易燃品、放射物品和腐蝕物品等八類，例如彈藥、軍用油料等[4]。軍用危險品車輛路徑選取原則有以下幾點：

（1） 安全性

軍用危險品運輸途中一旦發生事故，會嚴重危及道路周邊安全。本文用安全通過某一路徑的概率表示其安全屬性。

（2） 時效性

現代戰爭中，戰場形勢瞬息萬變，這就要求后勤保障工作的高效率。在軍用危險品運輸路徑選擇時必須考慮備選路徑的路線長度、路況、交通狀況等影響運輸時效的因素。

（3） 隱蔽性

軍用危險品運輸保密工作事關重大，必須選擇一條隱蔽、不容易遭受攻擊的運輸路徑，確保運輸安全。

3 應用案例分析

假定某地進行演練，一批航空彈藥需從某彈藥庫運往某基地，現有3條備選路徑，但每條路徑花費的時間、安全、距離等都不一樣。要求從這3條路徑中確定一個最佳行駛路線，根據以上各要素和指標給各方案打分。現利用層次分析法進行決策。

3.1 建立層次結構模型

針對軍用危險品運輸的特殊要求，在軍用危險品運輸路徑優化決策中主要考慮道路因素、運輸路徑事故率、影響人員分布、周邊安全等風險因素。我們把路徑選擇作為總目標層，把影響路徑選擇的風險因素作為準則層，把3個不同的路徑作為方案層。

3.2 構造比較矩陣

基于目標層的軍用危險品公路運輸路徑選擇的總目標，假定重要度權值，對準則層的影響要素進行成對的比較評價，結果如表3所示。

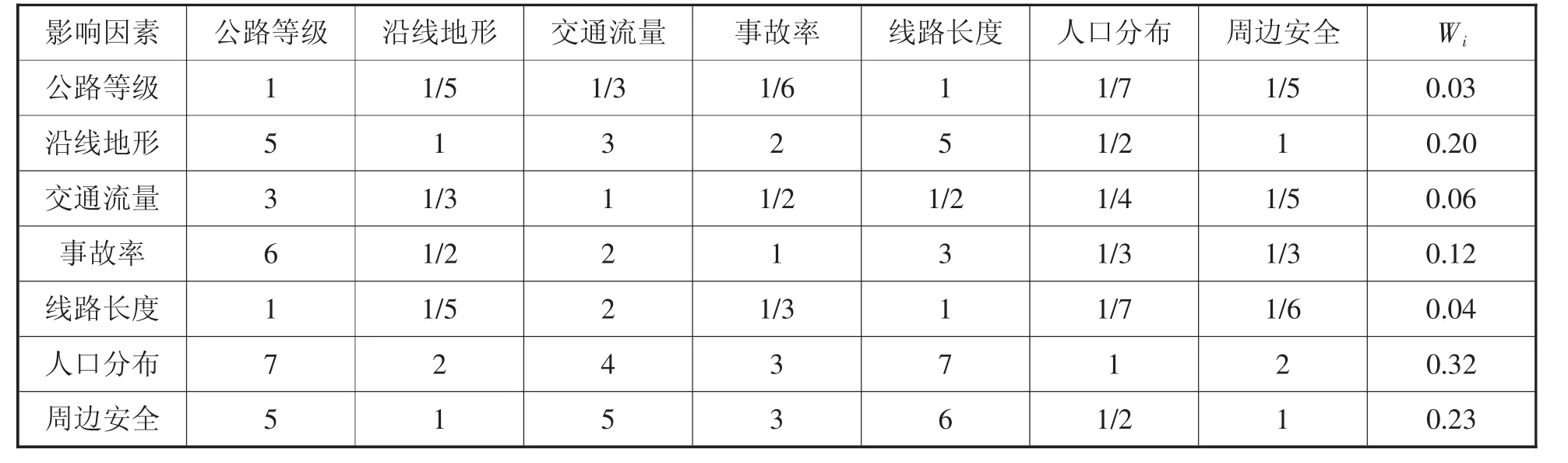
表3 準則層要素間的成對比較

由表3中數據列出判斷矩陣如下：

通過計算得到特征向量W=（0.03,0.2,0.06,0.12,0.04,0.32,0.23）T以及最大特征值：

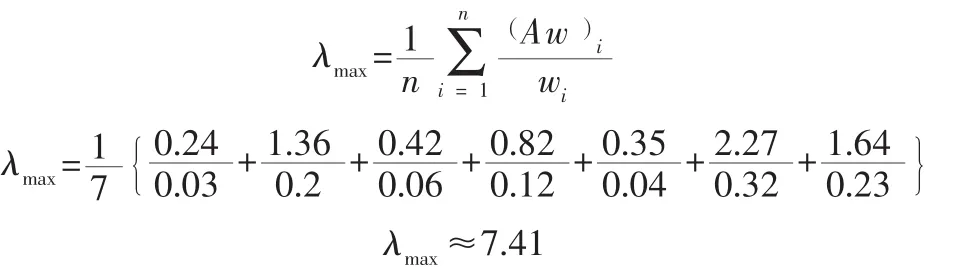
3.3 一致性檢驗

對矩陣A進行一致性檢驗：

經查表矩陣階數為7時R.I=1.32，因此：

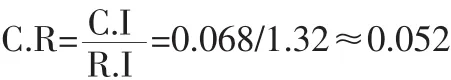
所以C.R＜0.1，滿足一致性要求。

3.4 構造方案層對準則層的比較矩陣

下面進一步評價3條備選路徑在不同影響因素下的優劣順序，分7個影響因素分別構建判斷矩陣，并計算出每個影響因素下3條備選路徑的優劣順序。

對于公路等級，構造出判斷矩陣，并求出各路徑的優劣順序，如表4所示。

表4 各路徑道路等級的成對比較

由表4中數據算出，λmax=3.07，C.I=0.035，R.I=0.58，所以C.R=0.06＜0.1，滿足一致性要求。

手術安全一直是當下各大醫院的重要關注點。近十年間，南大一附院強化了新技術準入管理和風險預警、追蹤管理，臨床醫學倫理委員會審核第一類醫療技術82項，并全部建立了新技術管理檔案。

對于沿線地形，構造出判斷矩陣，并求出各路徑的優劣順序，如表5所示。

表5 各路徑沿線地形的成對比較

由表5中數據算出，λmax=3.02，C.I=0.01，R.I=0.58，所以C.R=0.02＜0.1，滿足一致性要求。

對于交通流量，構造出判斷矩陣，并求出各路徑的優劣順序，如表6所示。

表6 各路徑交通流量的成對比較

由表6中數據算出，λmax=3，C.I=0，R.I=0.58，所以C.R=0＜0.1，滿足一致性要求。

對于交通流量，構造出判斷矩陣，并求出各路徑的優劣順序，如表7所示。

表7 各路徑事故率的成對比較

由表7中數據算出，λmax=3.45，C.I=0.23，R.I=0.58，所以C.R=0.39＞0.1，不滿足一致性要求，需要對判斷矩陣進行修正。

當C.R＞0.1，各要素的重要度自身的值缺乏信賴度，這就需要對判斷矩陣的值進行修正。一般使用一種相對簡單的方法解決判斷矩陣一致性不好的問題，具體操作步驟如下：

（1）利用求得的權重w1,w2,…,wn，以wi/wj為i,（）j的成分制作矩陣。

（3）找出差值較大的作為修正對象。

（4）對修正對象進行適當的調整。例如，aij為m，aik為n，akj為t，在實際比較時由于判斷偏差使得判斷矩陣不滿足一致性要求。通過一致性修正，找出aik和akj為修正對象，若aik/akj＞m，則將n適當減小，將t適當增大，使得aik/akj接近于m；反之，若aik/akj＜m，則將n適當增大，將t適當減小。

具體操作如下：

①利用計算求得的權重w1,w2,w3以wi/wj為i,（）j的成分制作矩陣，如表8所示。

②求得wi/wj與aij的差（取正值），如表9所示。

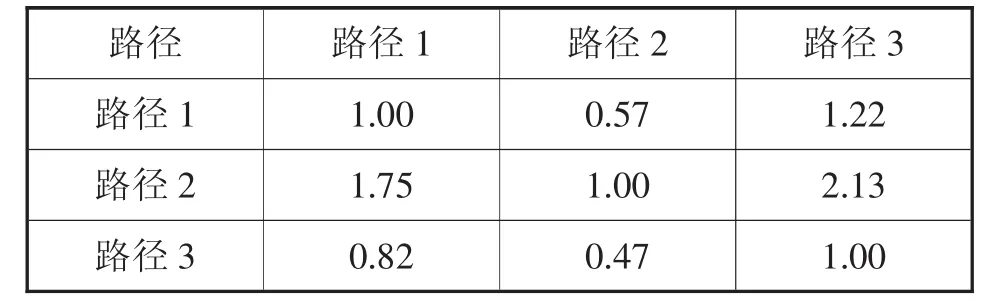
表8 wi/wj的矩陣

表9 wi/wj與aij差的矩陣

③找出差值比較大的成分作為修正對象。即a13=1.78，a23=1.87。

④對修正對象進行調整。由表知a12=1/2，而a13/a23=3/4，故不滿足一致性，所以應將a13適當調小，將a23適當調大。具體設定a13=2，a23=5，得到一個新的修正后的判斷矩陣，如表10所示。

由表中數據算出，λmax=3.01，C.I=0，R.I=0.58，所以C.R=0.01＜0.1，滿足一致性要求。

對于線路長度，構造出判斷矩陣，并求出各路徑的優劣順序，如表11所示。

由表11中數據算出，λmax=3.11，C.I=0，R.I=0.58，所以C.R=0.09＜0.1，滿足一致性要求。

對于沿線人口分布，構造出判斷矩陣，并求出各路徑的優劣順序，如表12所示。

由表12中數據算出，λmax=3.03，C.I=0，R.I=0.58，所以C.R=0.03＜0.1，滿足一致性要求。

表10 修正后的判斷矩陣

表11 各路徑線路長度的成對比較

表12 各路徑沿線人口分布的成對比較

對于沿線周邊安全，構造出判斷矩陣，并求出各路徑的優劣順序，如表13所示。

表13 各路徑沿線周邊安全的成對比較

由表13中數據算出，λmax=3.02，C.I=0，R.I=0.58，所以C.R=0.02＜0.1，滿足一致性要求。

根據上述計算方法及評定結果，計算路徑1，2，3的綜合評判值分別為0.3749，0.4105，0.2146。由此可知，路徑2為最優方案。故路徑2為本次軍用危險品公路運輸的最優運輸路徑。

4 結束語

通過層次分析法選擇分析，路徑1，2，3的綜合評判值分別為0.3749，0.4105，0.2146。可以看出路徑3的權重值相對更低，這是因為在路徑選擇時，充分考慮運輸的安全和時效性，而路徑3相對于其他兩條路徑，其經過的區域人口比較密集。而作為高速公路的路徑1的權重值低于作為三級公路的路徑2，是因為高速公路沿線地形相對簡單，不利于隱蔽，容易被打擊。因此，通過層次分析法綜合的權重分析，選擇路徑2作為最優運輸路徑。

通過層次分析法定量計算各備選路徑的綜合權重，最后根據所得權重確定最優路徑。文中例算表明，層次分析法能有效解決軍用危險品公路運輸路徑決策問題，從而變主觀為客觀，使路徑決策問題更加科學合理，具有更高的可信度。