單比特壓縮感知幀定時同步

王 維，卿朝進(jìn)，萬東琴，陽慶瑤

西華大學(xué) 電氣與電子信息學(xué)院，成都 610039

1 引言

作為數(shù)字通信系統(tǒng)的重要組成部分，幀定時同步是一直以來的研究熱點[1-2]。幀定時同步的性能直接影響通信系統(tǒng)性能，錯誤的幀定時同步將造成數(shù)據(jù)信息難以恢復(fù)。然而，日益增加的高數(shù)據(jù)速率需求使得幀定時同步面臨挑戰(zhàn)，是當(dāng)前通信系統(tǒng)亟待解決的問題之一[3-5]。

現(xiàn)有的相關(guān)法[6]、最大似然法[7-11]等幀定時同步方法的接收信號采樣速率需滿足采樣定理。隨著人們對高數(shù)據(jù)速率需求的日益增加，急切需要高采樣速率的模擬數(shù)字轉(zhuǎn)換器（Analog-to-Digital Converter，ADC）。然而，高的采樣速率導(dǎo)致系統(tǒng)高的能量消耗，造成ADC設(shè)計難度增加。文獻(xiàn)[2]提出了一種基于壓縮感知（Compressed Sensing，CS）的幀定時同步方法。相對于現(xiàn)有非壓縮感知幀定時同步方法，文獻(xiàn)[2]方法降低了系統(tǒng)的采樣速率，在一定程度上減少了系統(tǒng)的能量消耗，緩解了ADC設(shè)計難度。相對于壓縮感知技術(shù)，“單比特壓縮感知”[12]僅保留觀測值的符號信息，其量化過程通過簡單的電平比較器實現(xiàn)，可進(jìn)一步降低系統(tǒng)的能量消耗，降低模擬數(shù)字轉(zhuǎn)換器的設(shè)計難度。

為此，在文獻(xiàn)[2]的基礎(chǔ)上，本文將單比特壓縮感知技術(shù)引入到幀定時同步中，提出了一種基于單比特壓縮感知的幀定時同步方法。提出方法首先將接收信號映射到幀定時變換域，并在幀定時變換域?qū)邮招盘栠M(jìn)行單比特的壓縮采樣；隨后，根據(jù)二進(jìn)制迭代硬閾值（Binary Iterative Hard Thresholding，BIHT）算法[13]，利用采樣到的比特流重構(gòu)出用于幀定時同步的定時度量；最后，根據(jù)相關(guān)法幀定時同步準(zhǔn)則[6]，搜索重構(gòu)到的定時度量，找到幀定時同步的索引位置。分析與仿真結(jié)果表明，相對于壓縮感知幀定時同步方法，在相同的正確同步概率情況下，提出方法所用比特數(shù)更少；同時，提出方法的量化過程僅需電平比較器，降低了ADC設(shè)計難度。

2 單比特壓縮感知

本文將單比特壓縮感知技術(shù)引入到幀定時同步中。下面，首先對單比特壓縮感知技術(shù)進(jìn)行介紹。

單比特壓縮感知技術(shù)在2008年由Boufounos和Baraniuk提出[12]，其量化模型為：

其中，x是N×1的矢量，Φ是M×N的測量矩陣，y是對觀測值進(jìn)行單比特量化后的 M×1的矢量，即y=[ ]

y1,y2,…,yMT，sign(·)表示符號函數(shù)。根據(jù)文獻(xiàn)[7]，單比特壓縮感知的重構(gòu)過程可表示為：

其中，Y=diag(y)表示以矢量y的元素為對角元素的對角陣。

目前，基于單比特CS的重構(gòu)算法主要有固定點連續(xù)（Fixed Point Continuation，F(xiàn)PC）算法[14]、二進(jìn)制FPC[12]、匹配符號追蹤（Matching Sign Puisuit，MSP）算法[15]、限制步長收斂（Restricted Step Shrinkage，RSS）算法[6]、二進(jìn)制迭代硬閾值（Binary Iterative Hard Thresholding，BIHT）算法等。在上述算法中，BIHT算法是一種一階算法，是從標(biāo)準(zhǔn)CS重構(gòu)算法中的迭代硬閾值（Iterative Hard Thresholding，IHT）算法[16]發(fā)展而來的。該算法因其運行速度快，信號重構(gòu)效果好，收斂性強等特點[13]，而被廣泛應(yīng)用。鑒于此，本文采用BIHT算法對幀定時同步的壓縮采樣信號進(jìn)行重構(gòu)處理。

3 單比特壓縮采樣幀定時同步方法

3.1 單比特壓縮采樣

根據(jù)文獻(xiàn)[17]，Zadoff_Chu序列是一種恒包絡(luò)零自相關(guān)（Constant Amplitude Zero Auto-Correlation，CAZAC）序列，具有恒定的幅值特性、良好的自相關(guān)屬性以及良好的互相關(guān)屬性。因此，本文采用Zadoff_Chu序列作為訓(xùn)練序列。

根據(jù)文獻(xiàn)[1]，在采用非壓縮感知幀定時同步方法的情況下，接收機接收到的信號矢量r可以被表示為：

其中，r為N×1的接收信號矢量。c=(c0,c1,…,cL-1)表示長度為L的訓(xùn)練序列，d=(dL,dL+1,…,dN-1)表示長度為 N-L的數(shù)據(jù)信息；cd=(c0,c1,…,cL-1,dL,dL+1,…,dN-1)表示c和d的連接，T(·)表示循環(huán)移位運算，m表示待估計的幀的起始位置，即接收信號采樣序列與本地訓(xùn)練序列進(jìn)行滑動相關(guān)，然后搜索相關(guān)峰來獲得；n=(n0,n1,…,nN-1)為高斯噪聲，其組成元素ni，i=0,1,…,N-1是均值為0，方差為σ2的高斯隨機變量，圖1為幀定時同步的起點示意圖。

圖1 幀定時同步的起點示意圖

根據(jù)文獻(xiàn)[1]，定時度量可表示為：

式

（4）中，上標(biāo)“T”表示轉(zhuǎn)置運算，(·)modN表示每次對接收信號截取長度N。取

其中

c~由c和1×( N-L )的零向量串接形成，即

矢量x由定時度量Sc(0 ,r),Sc(1 ,r),…,Sc(N -1,r)組成，定時度量的幅度值 |Sc(0 ,r)|,| Sc(1 ,r)|,…,| Sc(N -1,r)|只有少部分非零，其余的為零，是典型的稀疏信號，或可壓縮信號。根據(jù)單比特壓縮感知原理，單比特壓縮采樣可表示為：

式（8）中，Y~表示單比特量化后的測量矢量。

3.2 定時度量重構(gòu)

本文采用BIHT算法對幀定時同步的定時度量進(jìn)行重構(gòu)處理。根據(jù)文獻(xiàn)[14，18-19]，目標(biāo)函數(shù)為ΦT(Y~-sign(Φxl))，將重構(gòu)定時度量的估計值映射到l2范數(shù)超球面上({ x ∈RN:‖x‖2=1} )。信號初始值取x0=0，則BIHT算法的迭代計算公式為：

其中，τ表示控制梯度下降步長的可調(diào)參數(shù)，Y~表示測量值的符號，A(xl)表示當(dāng)前信號估計值xl的測量值符號，即A(xl)=sign(Φ xl)。然后，通過硬閾值函數(shù)獲取信號估計值的K稀疏表征信號，即

BIHT算法重構(gòu)定時度量的模型可表示為：

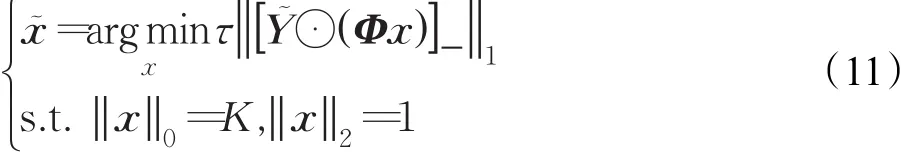
其中，[·]_表示負(fù)函數(shù)，u⊙v表示u與v的點積，(u ⊙v)i=uivi，ui與vi均為標(biāo)量。通過計算單邊l1范數(shù)最小，可以確保得到 yˉ⊙(Φ x )≥0。

定時度量的重構(gòu)過程如下所述[18]：

輸入：單比特觀測值Y~，觀測矩陣Φ，映射A，最大迭代次數(shù)lmax。

步驟1初始化x0=0，迭代次數(shù)l=0。

步驟2梯度計算βl+1=xl+ΦT(Y~-A(xl))。

步驟3硬閾值運算并映射到單位球上xl+1=ηK(βl+1)，（其中，ηK(·)為非線性算子，它將保留βl+1的前K個最大元素，其余元素置為零）。

步驟4計算nnz=‖Y~ - A(xl+1)‖0，比較符號不一致的個數(shù)。

步驟5更新迭代次數(shù)l=l+1。

步驟6若l＜lmax且nnz＞0時，返回執(zhí)行步驟2；否則執(zhí)行步驟7。

步驟7輸出xl+1=U(xl+1)，其中U(v)=v‖v‖2。

根據(jù)上述算法，當(dāng)重構(gòu)的定時度量與原來采樣值符號一致或者迭代次數(shù)達(dá)到最大時，BIHT算法終止迭代。

3.3 幀同步

根據(jù)相關(guān)法幀定時同步準(zhǔn)則，在對定時度量進(jìn)行重構(gòu)之后，搜索重構(gòu)到的矢量x~中幅度最大值的索引，找到幀定時同步的索引位置m~，即：

相對于文獻(xiàn)[2]方法，由于單比特壓縮，提出方法的量化過程僅需要簡單的電平比較器，這將會降低模擬數(shù)字轉(zhuǎn)換器設(shè)計的難度。

4 實驗仿真及分析

為驗證提出的單比特壓縮感知幀定時同步方法的有效性，給出相應(yīng)的數(shù)值仿真。根據(jù)文獻(xiàn)[20]，信噪比（Signal Noise Ratio，SNR）可表示為：

其中，Ps表示信號的功率，Pn表示噪聲的功率。

4.1 提出方法與文獻(xiàn)[2]和文獻(xiàn)[6]方法性能比較

為了驗證提出方法的有效性，本節(jié)將提出方法與文獻(xiàn)[2]和文獻(xiàn)[6]方法性能同時進(jìn)行比較。其中，文獻(xiàn)[2]為傳統(tǒng)壓縮感知幀定時同步方法，文獻(xiàn)[6]為傳統(tǒng)的“相關(guān)法”（非壓縮感知幀定時同步方法）。文獻(xiàn)[6]所述的“相關(guān)法”，其接收信號采樣速率需滿足奈奎斯特采樣定理；相對于文獻(xiàn)[2]和本文提出方法的壓縮采樣，文獻(xiàn)[6]方法的ADC設(shè)計更為困難。

4.1.1 正確同步概率的比較

在采樣所需的比特數(shù)相同的情況下，實驗驗證提出方法相對于文獻(xiàn)[2]方法（傳統(tǒng)壓縮感知幀定時同步方法）和文獻(xiàn)[6]方法（傳統(tǒng)的“相關(guān)法”，即非壓縮感知幀定時同步方法）的有效性。其中，文獻(xiàn)[6]和文獻(xiàn)[2]方法均采用16 bit量化器（采樣序列的實部和虛部分別進(jìn)行16 bit量化）。由于沒有壓縮采樣，文獻(xiàn)[6]方法所需的比特數(shù)為32N；文獻(xiàn)[2]方法所需的比特數(shù)為32M′（其中M′為文獻(xiàn)[2]方法測量次數(shù)）。考慮提出方法與文獻(xiàn)[2]方法所需比特數(shù)目相同，有M=32M′（其中M為所需比特開銷，即提出方法測量次數(shù)）。考慮文獻(xiàn)[6]方法與考慮提出方法（或文獻(xiàn)[2]方法）所需比特數(shù)目相同，取文獻(xiàn)[6]方法的幀長為N′時，有M=32N′。

仿真中，取訓(xùn)練序列長度L=64，幀長度N=2L=128，M′=N′=48，M=32M′=1 536。特別地，仿真給出了正確同步概率的比較的一個特例。將在4.2和4.3節(jié)分別驗證不同訓(xùn)練序列長度L和測量次數(shù)M對正確同步概率的影響，驗證提出方法的普適性，仿真結(jié)果如圖2所示。

圖2給出了正確同步概率與信噪比的關(guān)系曲線，從圖2可知：

圖2 正確同步概率與信噪比的關(guān)系曲線

（1）當(dāng)SNR≥25 dB時，提出方法與文獻(xiàn)[2]方法和文獻(xiàn)[6]方法均能達(dá)到近似為100%的正確概率。這說明在高SNR情況下（如該仿真所述的SNR≥25 dB），提出方法與文獻(xiàn)[2]和文獻(xiàn)[6]方法均能達(dá)到較高的同步概率。

（2）當(dāng)SNR＜20 dB時，在相同正確同步概率情況下，提出方法所需的SNR低于文獻(xiàn)[2]方法和文獻(xiàn)[6]方法所需的SNR。如，取正確同步概率近似為100%時，提出方法所需的SNR約為0 dB，而文獻(xiàn)[2]方法所需的SNR約為15 dB，文獻(xiàn)[6]方法所需的SNR約為25 dB。這從另外一個方面表明，在相同SNR情況下，提出方法獲得了更大的正確同步概率，即相對于文獻(xiàn)[2]和文獻(xiàn)[6]方法，提出方法改善了幀定時同步的正確同步概率。如，取SNR=5 dB時，提出方法的正確同步概率約為100%；而文獻(xiàn)[2]方法的正確同步概率約為0.56，文獻(xiàn)[6]方法的正確同步概率約為0.11。

4.1.2 所需比特數(shù)比較

在提出方法的正確同步概率不小于文獻(xiàn)[2]和文獻(xiàn)[6]方法的正確同步概率時，對比所需的比特數(shù)。取N=2L=128，仿真結(jié)果對比如圖3所示。

圖3 幀定時同步所需比特數(shù)與信噪比的關(guān)系曲線

圖3 給出了幀定時同步所需比特數(shù)與信噪比的關(guān)系曲線，從圖3可知：

（1）在提出方法的正確同步概率不小于文獻(xiàn)[2]和文獻(xiàn)[6]方法的正確同步概率時，對于相同SNR，提出方法的幀定時同步所需比特數(shù)均少于文獻(xiàn)[2]和文獻(xiàn)[6]方法的幀定時同步時所需的比特數(shù)。如SNR=5 dB時，提出方法幀定時同步所需比特數(shù)為512 bit；而文獻(xiàn)[2]方法幀定時同步所需比特數(shù)為2 048 bit，文獻(xiàn)[6]方法幀定時同步所需比特數(shù)為2 560 bit。

（2）相對于文獻(xiàn)[2]和文獻(xiàn)[6]方法，提出方法的量化過程僅需電平比較器，降低了ADC設(shè)計的難度。

為進(jìn)一步驗證提出方法相對于文獻(xiàn)[2]和文獻(xiàn)[6]方法的正確同步概率改善具有普適性，下面通過數(shù)值實驗分別驗證同步序列訓(xùn)練長度L和測量次數(shù)M對正確同步概率的影響。

4.2 訓(xùn)練序列的長度L對正確同步概率的影響

在采樣所需的比特數(shù)相同的情況下，實驗驗證提出方法相對于文獻(xiàn)[2]和文獻(xiàn)[6]方法在不同訓(xùn)練序列長度L的情形下的有效性。取壓縮采樣與量化后的比特開銷為M=2 048bit，幀長N=256，訓(xùn)練序列長度L分別考慮三種不同情形，即L=64，L=96和L=128。文獻(xiàn)[2]和文獻(xiàn)[6]方法仍考慮16 bit量化器，即 M′=N′=。仿真結(jié)果對比如圖4所示。

圖4 同步序列長度L的改變對仿真結(jié)果的影響

圖4 給出了不同訓(xùn)練序列長度L情況下正確同步概率與信噪比的關(guān)系曲線，從圖4可知：

（1）隨著L的增大，獲得接近100%的正確同步概率所需的SNR隨之減小。如為獲得近似100%的正確同步概率，提出方法在 L=64時，需SNR＞5 dB；而當(dāng)L=128時，提出方法僅需要SNR＞0 dB。類似的結(jié)果，也適用于文獻(xiàn)[2]和文獻(xiàn)[6]所述的幀定時同步方法。

（2）在相同SNR情況下，提出方法較文獻(xiàn)[2]和文獻(xiàn)[6]方法改善了正確同步概率（仿真給出的3種情形均有相同的結(jié)論）。如SNR=0 dB，L=96時，提出方法的正確同步概率約為100%；而文獻(xiàn)[2]方法的正確同步概率約為0.27，文獻(xiàn)[6]方法的正確同步概率約為0.05。

（3）根據(jù)（1）、（2）的分析，在相同的比特開銷情況下，提出方法改善了幀定時同步的正確同步概率。同時，由于單比特量化，提出方法量化過程僅需要電平比較器，提出方法相對于文獻(xiàn)[2]和文獻(xiàn)[6]方法降低了ADC設(shè)計的難度。

4.3 測量次數(shù)M對正確同步概率的影響

保證比特開銷相同，在幀長度N和訓(xùn)練序列長度L相同的情況下，實驗驗證提出方法相對于文獻(xiàn)[2]方法在不同測量次數(shù)M的情形下的有效性。取幀長度N=256，訓(xùn)練序列長度L=64。取壓縮采樣與量化后的比特開銷為Mbit，即提出方法的測量次數(shù)為M（測量次數(shù)M分別考慮三種不同的情形，M=1 024，M=2 048和 M=4 096）；文獻(xiàn)[2]方法仍考慮16 bit量化器，為了便于區(qū)分，將文獻(xiàn)[2]方法的測量次數(shù)表示為 M′，M′也考慮三種不同的情形，，仿真結(jié)果對比如

圖5所示。

圖5 測量次數(shù)M的改變對仿真結(jié)果的影響

圖5 給出了不同測量次數(shù)M情況下正確同步概率與信噪比的關(guān)系曲線，從圖5可知：

（1）隨著M的增大，獲得接近100%的正確同步概率所需的SNR隨之減小。如為獲得近似100%的正確同步概率，提出方法在M=1 024時，需SNR＞15 dB；而當(dāng)M=4 096時，提出方法僅需要SNR＞10 dB。類似的結(jié)果，也適用于文獻(xiàn)[2]所述的幀定時同步方法。

（2）在相同SNR情況下，提出方法較文獻(xiàn)[2]方法改善了正確同步概率（仿真給出的三種情形均有相同的結(jié)論）。如SNR=10 dB時，提出方法在M=1 024時，正確同步概率約為0.99；而文獻(xiàn)[2]方法在M′=32時，正確同步概率約為0.15。

（3）根據(jù)（1）、（2）的分析，在相同的比特開銷情況下，提出方法改善了幀定時同步的正確同步概率；在相同正確同步概率情況下，提出方法所用比特數(shù)更少。同時，由于單比特量化，提出方法量化過程僅需要電平比較器，再次驗證了提出方法相對于文獻(xiàn)[2]方法降低了ADC設(shè)計的難度。

5 結(jié)論

本文提出一種基于單比特壓縮感知的幀定時同步方法，以減少幀定時同步時所需的比特數(shù)，降低模擬數(shù)字轉(zhuǎn)換器設(shè)計的難度。該方法首先對接收信號進(jìn)行單比特的壓縮采樣，然后，對采樣到的比特流進(jìn)行重構(gòu)得到幀定時同步的定時度量，最后，根據(jù)定時度量的最大幅度值索引找到幀的起始位置。研究結(jié)果表明，相對于文獻(xiàn)[2]和文獻(xiàn)[6]所述的幀定時同步方法，在相同正確同步概率情況下，提出方法所需比特數(shù)更少；在相同的比特開銷時，提出方法相對于文獻(xiàn)[2]和文獻(xiàn)[6]可改善幀定時同步的正確同步概率。同時，提出方法的量化過程僅需要電平比較器，降低了模擬數(shù)字轉(zhuǎn)換器設(shè)計難度。仿真結(jié)果驗證了提出方法的有效性。