基于復雜網絡的全球海運網絡脆弱性分析

吳 姍，韓曉龍，劉嬋娟，胡志華

上海海事大學 物流科學與工程研究院，上海 200135

1 引言

海運網絡是由港口、海峽等節點和航線組成的復雜網絡，港口工人罷工、海盜、海上交通事故、自然災害等的擾動都會造成海運網絡節點失效。一個或多個節點失效會造成海運網絡通達能力下降，影響國際貿易往來。因此，對全球海運網絡脆弱性進行分析具有重要意義，有助于科學合理的制定海上運輸安全保障機制，且有助于航運企業有針對性的采取預防措施、制定適當的合作機制等。近年來，很多學者傾向于對航空、公路、鐵路等交通網絡以及電網的脆弱性和魯棒性進行分析及優化，但對海運網絡脆弱性的研究還不多。

脆弱性的概念最早是由Timmerman[1]提出的，脆弱性是一種度，即系統在災害事件發生時對系統產生不利影響的程度。Berdica[2]最早將脆弱性概念引入道路交通網絡中，認為脆弱性是由于不同原因導致可達性下降的特性，將脆弱性定義為交通系統對于異常事件的易受影響性。對于路網脆弱性的研究，Husdal[3]研究脆弱性聚焦于路段或整個網絡在各種非正常狀況下無法運轉的特性。Woolleymeza等[4]研究世界海運網絡和航空網絡具有類似的拓撲結構特性，在面對故障和攻擊時表現出了相似的魯棒性和脆弱性。Crucitti等[5]在交通網絡中，采取有選擇刪除（蓄意攻擊）網絡的部分節點或者邊時對網絡連通性的影響程度。田煒等[6]等對馬士基航運的海運網絡進行了實證分析，認為世界海運網絡局部節點間最短路徑過大，大部分節點具有較大的聚集系數等特征。牟向偉和陳燕[7]利用復雜網絡理論對班輪航運網絡的拓撲特征進行了統計分析。姚紅光和朱麗萍[8]以最大連通子圖的相對大小作為基本指標來度量航空網絡的魯棒性。王杰和李雪[9]以復雜網絡理論為基礎，分析了海運網絡的拓撲結構，驗證了海運網絡具有小世界和無標度網絡特征。黃常海[10]基于復雜網絡理論研究了內河航道網絡的脆弱性。王諾[11]研究了網絡壓力測試方法，探究全球集裝箱海運網絡脆弱性的變化趨勢。張廣勝等[12]分析物流服務供應鏈網絡節點作用規律，引入聚集系數、最大連通度及連通效率作為網絡脆弱性測度指標，基于所構建攻擊策略對二級物流服務供應鏈網絡進行實例研究。程光權[13]等提出一種基于節點狀態演化級聯失效模型的節點重要度評估和網絡脆弱性分析方法。

由以上分析可知，國內外學者對于交通網絡脆弱性的研究主要集中于航空運輸網絡和公路網絡，對于海運網絡的研究鮮少，且已有研究大多只是分析海運網絡拓撲結構，而并未對全球海運網絡脆弱性進行分析。本文基于復雜網絡理論和方法，在全球海運網絡拓撲結構的基礎上從全局角度對全球海運網絡脆弱性進行分析，并用MATLAB分析港口度、平均聚集系數、網絡平均距離等指標，最后定量計算各個港口的脆弱性，同時比較全球集裝箱海運網絡在面對不同方式下的攻擊時的海運網絡脆弱性變化。從局部到整體對海運網絡進行脆弱性研究，為日后對海運網絡優化和對航線或港口由某種原因短暫性失效提供理論解決依據。

2 數據采集

以往研究多采用馬士基集團下的航運數據進行實證分析，為了統計數據的完整性，力求構建最能反映真實情況的海運網絡，本文以世界前10大班輪公司中7家公司的航運數據為研究基礎。這7家公司所占全球海運運輸市場份額合計達45.6%，如表1所示。雖然市場份額不大，但總的服務網絡已遍布世界6大洲，涉及全球最基本的海運港口，所以該航運數據基本可以代表目前全球國際航運狀況。以各船公司（馬士基、達飛、赫伯羅特、長榮、中遠、中海和韓進）網站的船期表為基礎，分別跟蹤和獲取每條航線上一個航期中班輪掛靠的所有港口，跟蹤時間為2015年10月到2016年1月。經過港口名稱規范化后，統計得港口總數為777個，所涉及的航線總數為7 553條。

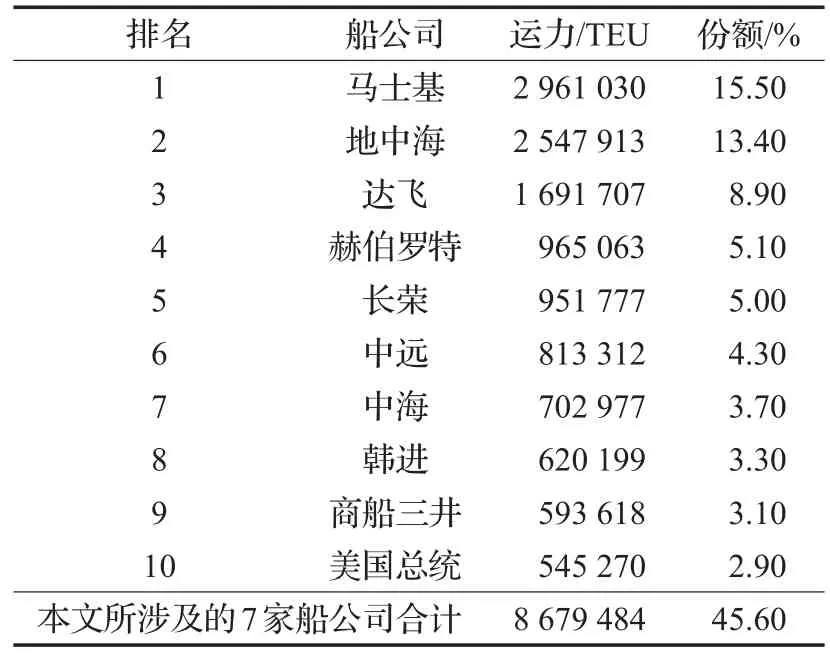
表1 7家主要航運公司TEU及市場份額

為便于理論分析，將全球集裝箱海運網絡中的各個港口抽象為網絡中的各個節點，港口之間航線抽象為邊，構建一個簡單的無向無權網絡。以V={ }1,2,…,N表示港口的集合，N表示港口總數。Ri,j表示港口i和港口 j之間是否存在班輪航線。若i和 j之間存在邊的連接，則Ri,j≠? 且Ri,j?R；若i和 j之間尚未建立連接，則Ri,j=?。其矩陣表達式為：

式（1）中eij=0或eij=1分別表示港口i和港口 j之間不存在或存在邊的連接，據此得到一個777×777的0-1矩陣。

應用UCINET軟件繪制全球集裝箱海運網絡拓撲結構圖，為增強顯示效果，本文選擇港口節點連邊數前100位（度值前100位）港口進行了顯示，如圖1所示。

3 海運網絡拓撲結構參數統計

3.1 度與度分布

在復雜網絡中，度是節點的重要特性之一，某一節點i的度k是指與該節點相連接的節點的數目。在海運網絡中，度值較大的節點則表明有較多的航線經過該港口。

港口i的度是指與此港口連接的其他港口數目，用N(k)表示；網絡中港口的度分布概率用度分布函數P(k)表示，其含義是隨機選擇一個節點恰好連接k條邊的概率。其中，N為港口總數，P(k)為度是N(k)的節點數占網絡節點總個數的比例。計算公式：

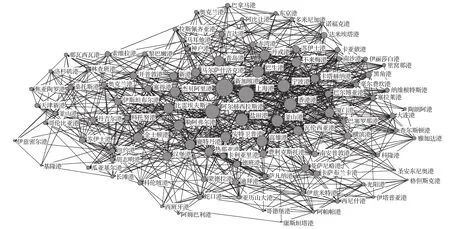
圖1 度值前100港口集裝箱海運網絡拓撲結構圖

根據節點度分布函數P()k以及全球777個港口的航線數據，得出全球集裝箱海運網絡各節點度值及度分布分別見圖2、圖3。其中，網絡中節點度值最大為138，平均度值為=9.720 7，說明在全球集裝箱海運網絡中經過任一港口的航線數平均約為10條。

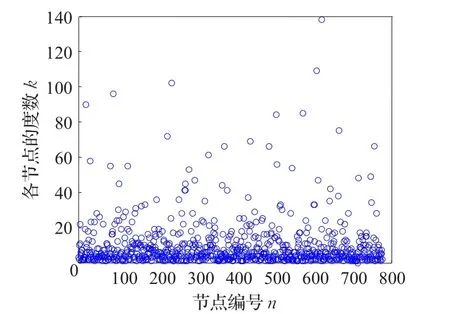
圖2 海運網絡各節點度值

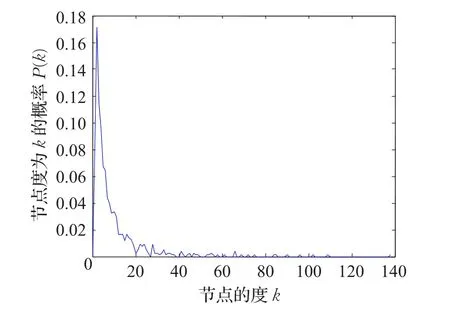
圖3 海運網絡各節點度分布

3.2 網絡聚集系數

在海運網絡中，聚集系數的分布反映航線的密集程度，其中網絡聚集系數對海運網絡脆弱性的影響呈負相關，聚集系數越大，該網絡對其節點產生的影響越大。節點的網聚集系數是計算網絡中描述中各港口的聚集情況，即網絡的緊密程度，設C為網絡聚集系數，有：

式中，E(i)表示節點i的鄰居節點之間實際的連接邊數，T(i)表示節點i的k個鄰居節點之間可能形成的最大連接數，設節點i的度為k，易知，T(i)=k(k -1)2。因為N為港口總數，所以整個網絡中所有節點的平均聚集系數c(s)，有：

其中0≤c(s)≤1，當c(s)=0時，表示所有節點都是孤立節點，沒有邊連接；當c(s)=1時，表示網絡成為兩兩節點之間完全的邊連接。根據公式（4）以及全球777個港口的航線數據，計算得出整個網絡平均聚集系數為c(s)=0.484 4，說明全球航線的分布較為密集。

3.3 網絡平均距離

網絡的平均最短路徑L是指網絡中所有節點對間的最短路徑的平均數。一般貨物運輸過程中停靠的港口數越少越好，這樣既可以節省時間，也能保證貨物質量安全。在無向無權網絡中，任意兩個節點i和 j之間的距離dij被定義為這兩個節點的最短路徑所包含的邊數。網絡的平均最短路徑L是指網絡中所有節點對間的最短路徑的平均數，如公式（5）所示。其中N為網絡節點總數。

通過以上計算、分析可以看出全球海運網絡的節點度分布基本滿足截斷遞減冪律分布，度值大的節點所占比重較小，而度值小的節點占比重較大。全球集裝箱海運網絡中網絡平均距離分布曲線見圖4。

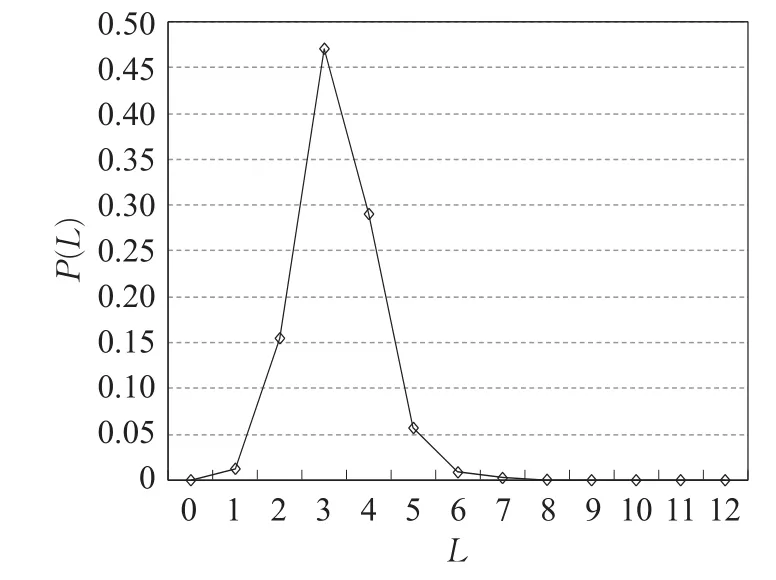
圖4 全球集裝箱海運網絡中平均最短路徑分布

根據圖4可知，集裝箱海運網絡中網絡平均距離近似服從正態分布，大多數節點對之間的網絡平均距離集中在2～5之間，說明在全球集裝箱海運網絡中，將一票貨物從一個港口送達至另一港口平均所需停靠的港口數量約為3或4個。

4 全球集裝箱海運網絡脆弱性分析

4.1 基于節點脆弱度的關鍵節點識別

依靠網絡拓撲參數指標能夠判定一些重要節點，如根據度值大小，聚集系數等。但是，僅僅依靠拓撲指標來判定節點在網絡中的重要性是不全面的。因此，本文中提出節點脆弱度的概念來識別全球集裝箱海運網絡中的關鍵港口。

根據文獻[14-15]對網絡效率的定義：節點i和節點j之間的網絡效率用eij表示，eij可以看做是節點i和節點 j之間最短路徑長度dij的倒數，如式（6）所示。如果節點i和節點 j之間無連接存在，那么eij為0。整個網絡的效率可以表示為式（7）。記原始網絡的網絡效率為E，某個節點失效后的網絡效率為Er，那么某節點r的結構脆弱度如式（8）所示。根據公式（7）求得原始海運網絡拓撲結構的網絡效率為0.332 8。

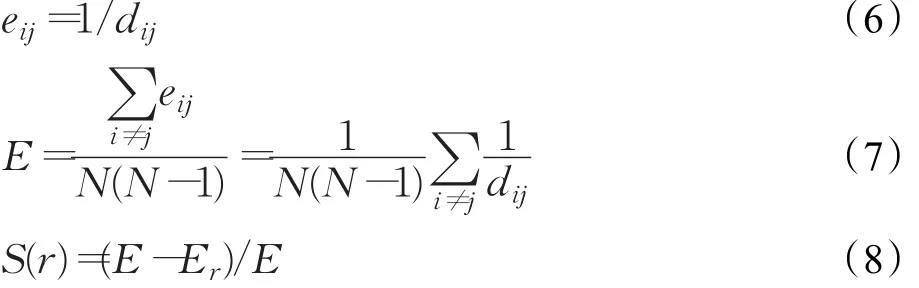
運用MATLAB編程求解各節點脆弱度，編程對數據進行處理，可得出不同節點失效后各節點的脆弱度，表2是脆弱度前60的節點排名。

由表2可以看出，舟山港的脆弱度最大，為0.332 9，其次為澤布呂赫（比利時西部的一個港口）、中山港、張家港、漳州港、湛江港、乍浦港（嘉興港）、肇慶港、鎮江港、日本四日市港。舟山港的結構脆弱度最大的主要原因是，舟山港是一個以水運中轉為主要功能的深水良港，與寧波港合并后，資源得到了整合，在整個海運網絡中直接相連的航線數量增多，充當了更多港口對的中介作用，這一港口失效后，會嚴重影響網絡的結構性能，甚至造成網絡癱瘓，這也體現了舟山港在整個海運網絡中的重要性和樞紐地位。貨物吞吐量較大的上海港、新加坡港、鹿特丹港、黑德蘭港等在世界集裝箱海運網絡中的脆弱度并不大。因此，不能僅僅根據港口貨物吞吐量來判定一個港口在全球海運網絡中的重要性。

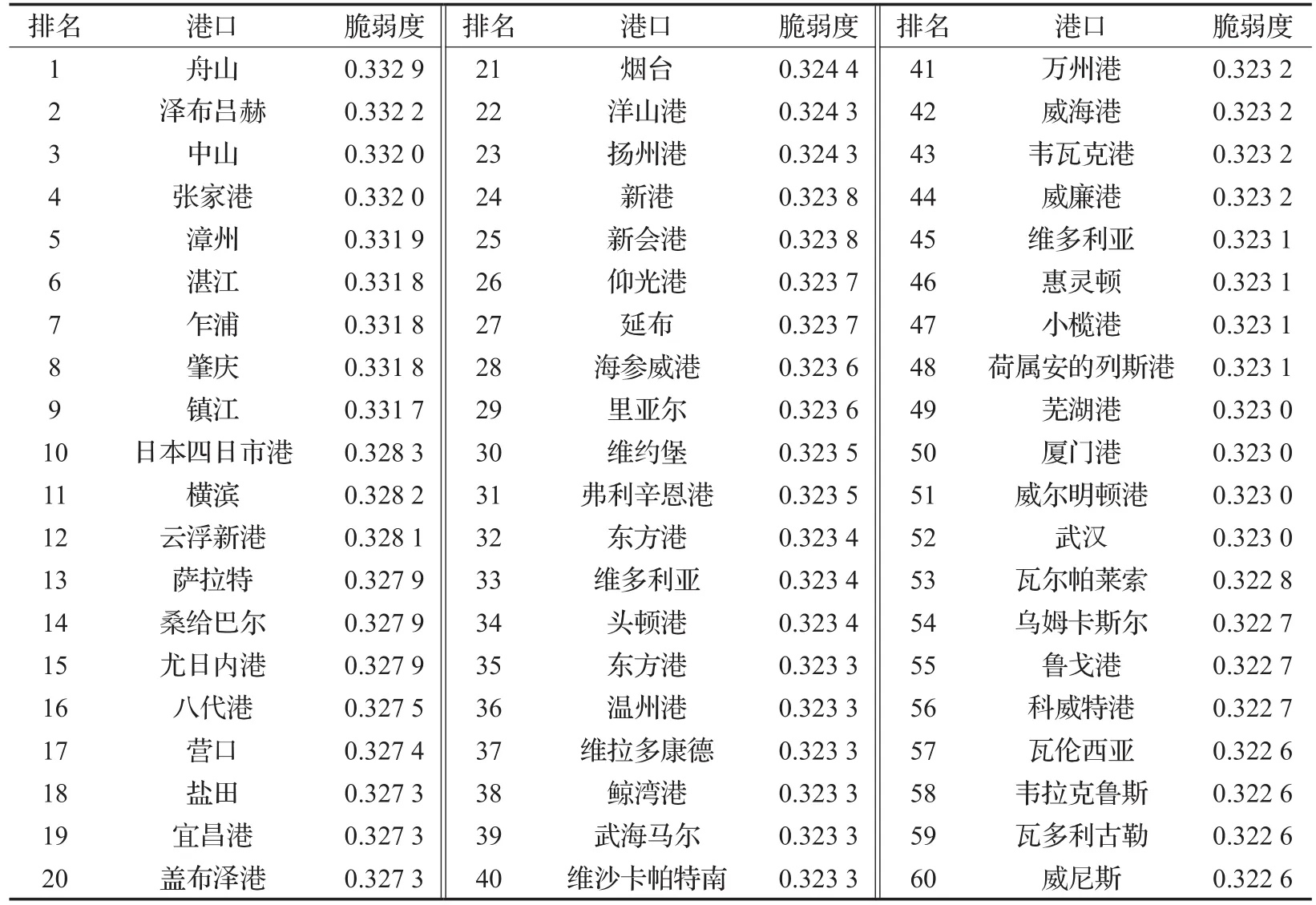
表2 港口脆弱度計算結果（前60）

4.2 全球集裝箱海運網絡全局脆弱性分析

全局脆弱性是從整體的角度分析網絡的脆弱性，了解整個海運網絡在內部或外部的某些誘因下而引起的網絡連通性的變化。這些誘因包括：海運網絡拓撲結構的不合理、自然災害、海盜及海上恐怖主義、政治因素、海上交通事故等多種因素。為了區分攻擊方式的不同對港口脆弱性分析的不同影響，這里把攻擊模式分為隨機攻擊和蓄意攻擊兩種。

在隨機攻擊模式下，海運網絡中的各個節點具有相同的被攻擊概率，每次隨機攻擊網絡中的某個節點以及與之相連的邊，并計算節點移除后網絡效率等性能指標的變化情況。隨機攻擊主要測試隨機事件對海運網絡中航線通達能力的影響。

在蓄意攻擊模式下，按照節點脆弱度的大小對所有節點進行排序，最先移除具有最大脆弱度的節點，如果網絡中有多個節點具有相同的脆弱度，隨機移除其中一個節點即可，移除網絡中節點脆弱度最大的節點后，計算網絡中各項性能指標，然后重新移除網絡中節點脆弱度最大的節點，重復進行下去直到達到預設條件。

本文應用MATLAB軟件，設計對全球集裝箱海運網絡進行隨機攻擊和蓄意攻擊兩種攻擊策略，計算受到攻擊后的網絡效率。全局脆弱性分析計算具體步驟歸納如下：

步驟1利用初始網絡拓撲結構，求出關鍵的節點指標P(k)、c(s)和L。

步驟2按照不同攻擊模式的刪除策略選取被攻擊的節點，移除網絡中的相應節點。

步驟3根據新的網絡拓撲結構，計算出網絡效率E和脆弱度S(r)。

步驟4判斷是否符合預設條件，若結果不符合條件，返回步驟2，反之，算法結束。

按上述步驟，計算得出在不同攻擊模式下，隨著攻擊節點數的增加，網絡效率的變化情況。隨機攻擊和蓄意攻擊下網絡效率計算結果見表3，網絡效率走勢圖見圖5。

根據圖中曲線走向可以得知，在蓄意攻擊下指標下降速度更快，隨著被攻擊節點數量的增加，指標下降速度逐漸變快。蓄意攻擊比隨機攻擊對網絡的破壞程度大，這是因為蓄意攻擊模式下每次刪除網絡中脆弱度最大的節點，這些節點對海運網絡的連通性和穩定性起著非常重要的作用，攻擊這些節點會使網絡的拓撲結構發生劇烈的變化，從而使網絡的網絡效率迅速減小。全球集裝箱海運網絡在面對蓄意攻擊時表現出較大的脆弱性，因此應該重點關注蓄意攻擊可能引發的網絡脆弱性，對脆弱度較高的港口加強預防，切實保障這類港口的正常高效運行。

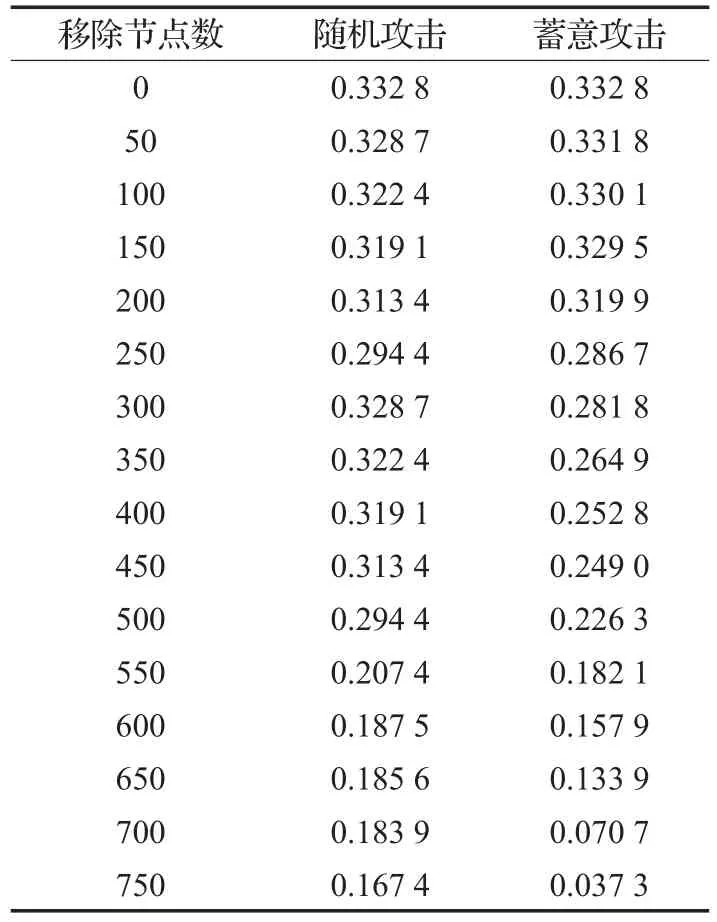
表3 兩種不同攻擊方式下網絡效率變化表

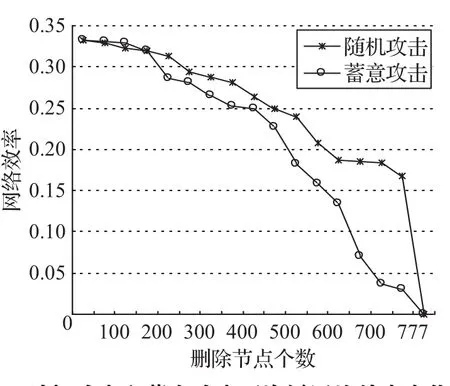
圖5 隨機攻擊和蓄意攻擊下海運網絡效率變化圖

為提升各節點的彈性，脆弱度較高的港口可以選擇與鄰近的脆弱度稍低的港口進行合作，當脆弱度較高的港口因不可抗力造成中斷時，合作港口可以及時響應，協助處理受攻擊港口在中斷期間的業務。此外，脆弱度較高的港口也可以協助鄰近的脆弱度稍低的港口進行業務水平的拓展，均衡各港口在航運網絡中的不可替代性程度，降低其自身的脆弱度。在實際港口分布中，有很多臨近的港口形成雙、多核協同港，如寧波港、舟山港與上海港，香港港與深圳港，新加坡港與巴生港等。這些相鄰的節點類似于計算機備份機制，一旦某一港口在某種情況下部分或全部短暫性失效，這些相鄰的協同港口立即承擔起航運運輸功能，港口間協同合作可以使集裝箱海運網絡失靈后受到的影響減少。

5 結論

本文基于復雜網絡理論和方法，在搜集了2015年最新全球10大班輪公司中7家航運公司數據的基礎上構建了全球集裝箱海運網絡的拓撲結構。首先計算能夠揭示拓撲網絡結構特性的相應參數；然后提出脆弱度的概念來進行網絡中關鍵節點識別，分析得出舟山港脆弱度最大，為0.332 9，而貨物吞吐量較大的上海港、鹿特丹港、新加坡港等的脆弱度并不大，因此，不能僅僅根據港口貨物吞吐量來判定一個港口在全球海運網絡中的重要性。最后應用MATLAB軟件進行仿真實驗，從全局脆弱性角度分析海運網絡脆弱性。仿真實驗結果表明全球集裝箱海運網絡在面對蓄意攻擊時表現出較大的脆弱性，在移除相同節點數時，蓄意攻擊的網絡效率明顯低于隨機攻擊下的網絡效率。因此，為了保障全球海上運輸的安全性和可靠性，應該對全球集裝箱海運網絡中脆弱度較大的舟山港、澤布呂赫中山港、張家港、漳州港、湛江港等加以重點保護。

海運網絡脆弱性分析能夠為集裝箱海運網絡的規劃、加強重點航線的維護、應急運輸備用港口及航線選擇等提供理論依據。針對集裝箱航線上可能發生的各種突發事件，建立相應的場景，分析脆弱度變化，為重新優化航運線路提供幫助。對于網絡脆弱性分析，考慮各個港口和海運航線失效的概率和時間等方面，將是本文后續研究的方向。