基因編輯差分算法在多燃料經濟調度中的應用

孟安波，林藝城

廣東工業大學 自動化學院，廣州 510006

1 引言

在電力系統運行中，經濟調度（Economic Dispatch，ED）是一項重要的優化任務，其主要目標為在滿足出力—負荷平衡的等式約束和發電機出力等不等式約束條件的前提下，使得總發電成本最小，對電力系統的安全經濟運行具有重要的意義[1]。傳統ED優化問題中，發電機組進氣閥突然開啟所產生的拔絲現象——閥點效應往往被忽略不計，這降低了模型的求解精度[2]。同時，僅能利用單一燃料的傳統發電機組已經不能滿足經濟和環境的需求，因此能使用多種燃料的發電機組成為目前火力發電的主流。本文ED模型中同時考慮了發電機組的閥點效應和多燃料。計及閥點效應給ED問題的尋優空間增加了大量的局部最優點，而考慮多燃料則使得ED的解空間不連續，因此該問題呈現出一系列高維、非凸、非線性、不連續的特點，進一步增加了問題的解決難度。隨著系統工程理論研究的日趨成熟和現代計算機技術在計及閥點效應和多燃料經濟調度領域的不斷發展與應用，各種新方法和新技術也層出不窮。常見有傳統的數學優化方法：如線性規劃[3]、非線性規劃[4]、動態規劃[5]等，傳統的優化方法過度依賴數學模型，并在求解時需將數學模型進行簡化，且對初始解較為敏感，因此在處理此類計及閥點效應和多燃料的復雜DE優化問題時容易陷入局部最優點。近年來，智能優化算法得到了高速發展，因此，在解決多燃料DE問題上大量地采用啟發式優化算法，如原始的啟發式優化方法，主要有遺傳算法（GA）[6]、粒子群算法（PSO）[6]、差分算法（DE）[7]、重力搜索算法（GSO）[8]、競拍分布式算法（AA）[9]、布谷鳥搜索算法（CSA）[10]、禁忌搜索算法（TSA）[6]、生物優化算法（BBO）[11]、搜尋者優化算法（SOA）[12]等。相對于傳統數學優化方法，這些原始啟發式算法對所求問題的數學模型沒有特殊限制，具有強大的適應性。然而，原始算法仍存在容易出現過早熟現象，收斂精度不高等缺陷。因此，更多的學者致力于研究其改進方法，如從算法結構上的改進，主要有改進遺傳算法[7，13-14]、改進粒子群算法[7，15-20]、改進布谷鳥算法[21]、改進蛙跳算法[22]、擾動差分算法（SDE）[23]、全局最優和聲搜索算法（GHS）[23]等，或結合兩個及以上算法的混合，如混合遺傳乘數更新算法[24]、混合分布式粒子群和禁忌搜索算法[25]等[7，19，23，26-27]，這些改進或混合算法比原始算法適應性更強，優化結果也更具優勢，然而這些算法在面臨不可微、不連續、非凸、非線性的大規模計及閥點效應的多燃料經濟調度優化問題時，同樣也存在一些缺陷，如種群多樣性不足，容易陷入局部最優，收斂速度較慢等，因此，需要提出一種更高效的方法解決該優化問題。

差分進化（Differential Evolution，DE）算法[28]的基本思想是仿照生物進化機制，利用種群中個體間的差異產生新的個體，然后進行交叉、選擇操作以實現種群的進化，并通過多次迭代搜索最終得到全局最優解。DE算法不但具備結構簡單、控制參數少、易于實現、有較強的魯棒性等優點，而且其固有的并行性有助于算法求解大規模系統模型。尤其是在低維單峰函數優化問題中具有明顯的收斂速度快、尋優精度高等優勢。然而在面臨高維、多峰、非線性及不可微等復雜優化函數時，存在后期收斂速度慢，容易陷入局部最優等缺陷。針對這一問題，本文首次提出了基因編輯差分算法（Gene Editing Differential Evolution，GEDE），該算法在標準差分算法的基礎上，通過融入最新研制的基因編輯操作，該操作能有效緩解DE算法后期收斂種群多樣性不足導致陷入局部最優的現象，并且在收斂后期種群中個體嚴格滿足等式約束情況下，每次基因編輯操作均為在可行域中搜索，這極大地降低了整個搜索空間，大幅度地提高算法搜索效率。此外，本文將通過10機組和40機組的多燃料電力系統的算例進行仿真分析，并與文獻所提多種方法進行綜合對比，驗證所提算法在求解高維、非凸、不連續的計及閥點效應的多燃料經濟調度優化問題時的有效性與優越性。

2 經濟調度模型

2.1 傳統的經濟調度目標函數

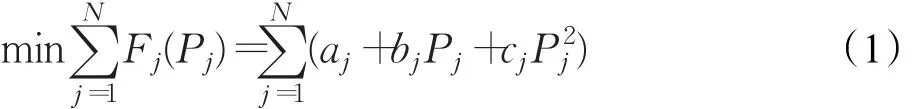
式中Fj為機組 j的燃料費用；N為發電機組數；aj、bj、cj為發電機組 j的燃料費用系數，Pj為發電機組 j的出力。

傳統ED問題的主要目標是在滿足電力系統安全運行的各種約束下，通過優化各發電機組有功出力使得所有發電機總燃料費用最小，其目標函數為：

2.2 計及閥點效應經濟調度目標函數

在實際的經濟調度中，通常還需考慮汽輪機進氣閥突然開啟所出現的拔絲現象，該現象會在機組的耗量特性曲線上疊加一個如圖1的脈動效果——閥點效應，可表示為：

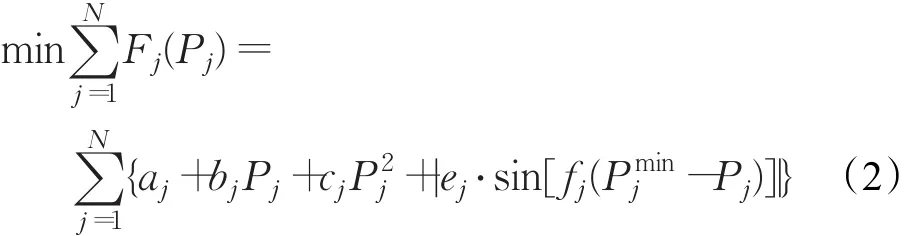
式中ej、fj為發電機組 j的閥點效應系數；Pminj為發電機組 j的最小技術出力。

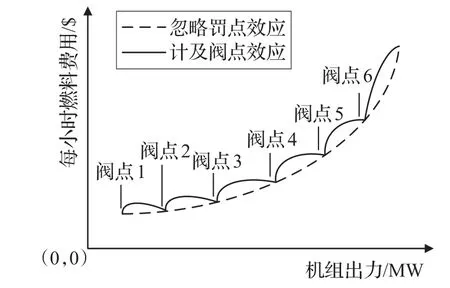
圖1 計及與忽略閥點效應的火電廠耗量特性曲線對比圖

2.3 計及閥點效應和多燃料的經濟調度目標函數

當發電機組同時考慮閥點效應和多燃料時，機組的耗量特性曲線將出現如圖2所示的分段脈動效果，該數學模型可表示為：

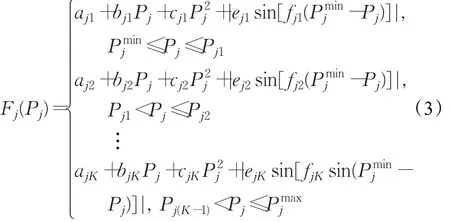
式中ajK、bjK、cjK、ejK、fjK為機組 j的第K種類型燃料的費用系數，該分段函數共有K段；為機組 j的最大出力。

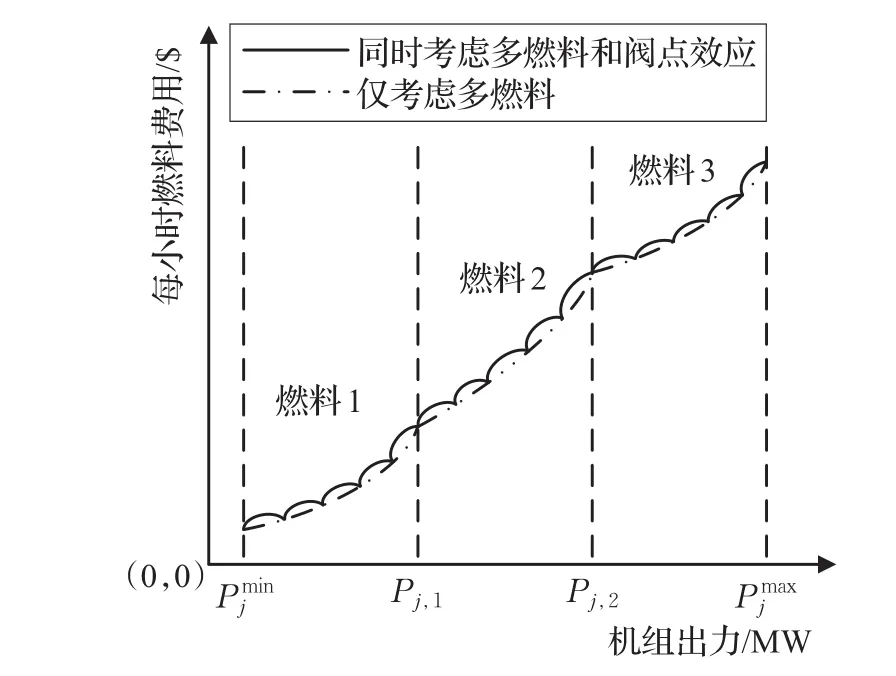
圖2 同時考慮多燃料和閥點效應的機組油耗特性曲線

2.4 約束條件

（1）負荷平衡約束

式中，PD為系統負荷需求。

（2）機組出力約束

3 基因編輯差分優化算法

3.1 標準差分進化算法

與遺傳算法相似，DE算法也包含交叉、變異和選擇操作，不同的是，DE在隨機選擇的父代個體間差分矢量的基礎上生成變異個體；其次，按一定的交叉概率對父代個體與變異個體執行交叉操作，生成試驗個體；最后采用貪婪策略保留父代個體與試驗個體之間適應值較好的個體。

3.1.1 變異操作

DE算法是在父代個體之間差分矢量的基礎上執行變異操作的，每個差分矢量包含父代（如第g代）的兩個不同個體。實際應用中DE有多種變異方案[29]，其變異個體的生成方式也各有差異。本文采用的變異操作具體如下：

式中，g 為當前代數；r1、r2、r3∈N(1,M)?r1≠r2≠r3≠i；為第g代變異個體i；、、為第g代種群中隨機挑選的互不相同個體；G∈[0,2]為縮放比例因子，用于控制差分矢量-對個體的影響。

3.1.2 交叉操作

DE算法通過交叉操作以提高種群的多樣性。該過程根據當前種群中個體和變異操作所產生的變異個體實施交叉操作，產生試驗個體，具體交叉方式如下：

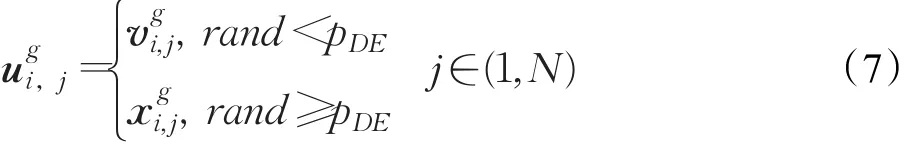
式中，rand為[0，1]之間服從均勻分布的隨機數；pDE∈[0,1]為交叉概率；N為變量的維數。

3.1.3 選擇操作

3.2 基因編輯差分算法

標準DE算法的性能主要取決于其全局搜索和局部探測能力，在一定意義上，這取決于該算法的種群大小、縮放比例因子、交叉概率等控制參數的設置，相比于其他的啟發式算法而言，DE算法具備控制參數少、可操作性強、群體搜索、具有記憶個體最優和全局最優的保優功能等優點。然而，與其他諸如遺傳算法、蟻群算法、粒子群算法等絕大多數啟發式算法相似，DE算法由于自身固有利用差分向量進行突變產生新個體的搜索方式造成該算法在當迭代次數達進行到一定次數時，種群多樣性的急劇下降，形成“聚集”現象，導致過早收斂的問題。

為增強DE算法的全局收斂能力，使算法在處理高維多峰復雜優化問題時，降低算法在某一局部最優點出現停滯的可能性，避免種群多樣性過早喪失，協助其跳出局部最優。本文通過在上述標準DE算法的基礎上融入最新研制的基因編輯技術操作，其實現過程如圖3所示。

細胞核（種群）中染色體（個體）的所有基因（維）進行兩兩不重復配對，并依據編輯概率 pc判斷配對基因是否執行基因編輯操作，若rand＞pc則執行基因編輯操作，假定染色體i中的d1、d2維基因分別為 x(i,d1)和x(i,d2)，則對它們進行基因編輯操作產生修復的d1、d2維基因可表示如下：

（1）基因定點剪切、供體重組

式中，L(d1)、L(d2)為基因保守序列（分別為第d1、d2維元素對應的下限）；gd為所提取的基因供體。

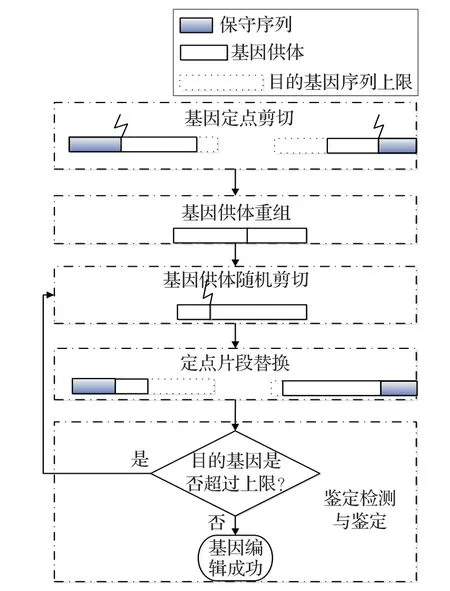
圖3 基因編輯技術操作的實現示意圖

（2）基因供體隨機剪切

式中，gs1、gs2分別為剪切后的基因供體片段。

（3）定點基因片段替換

式中，gr(i,d1)、gr(i,d2)分別為染色體i修復后的第d1、d2維基因。

基因檢測與鑒定：若 gr(i,d1)≤U(d1)且 gr(i,d2)≤U(d2)，則基因編輯成功，轉至判斷下一配對基因是否執行基因編輯操作；若否，則轉至步驟（2）重新進行基因供體隨機剪切，直至基因編輯成功。

與DE算法的選擇操作相同，執行完基因編輯技術操作的染色體需與父代染色體進行比較，擇優保留進入下一次迭代。

本文所提GEDE算法在DE算法的研究基礎上，融合了基因編輯技術操作，該操作通過采用一個編輯概率pc控制當前細胞核內所有染色體參與編輯的基因規模，這有利于協助部分維擺脫維局部最優的同時避免破壞正常維，有效地避免算法過早熟收斂。其次，由上述基因編輯技術操作過程不難發現，該操作并不會發生基因漂移，即基因編輯技術操作后配對維之和保持不變。因此，隨著搜索的逐步深入，當出現細胞核中染色體上所有基因之和嚴格滿足如式（4）中等式約束時，此時所執行的每次基因編輯技術操作將同樣嚴格滿足等式約束，對于上述計及閥點效應的多燃料經濟調度更是同時滿足等式約束和不等式約束，即每一次基因編輯技術操作均在可行域上搜索全局最優解，這極大提高了算法的計算效率，此過程可由圖4所示。

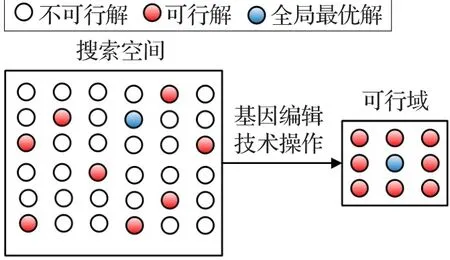
圖4 基因編輯技術操作搜索范圍變化示意圖

4 GEDE算法基本步驟

步驟1設定種群大小M、最大迭代次數maxgen、交叉概率pDE、編輯概率 pc，在解空間中隨機初始化種群，并計算每個個體的適應度值。

步驟2對種群中所有個體執行變異、交叉和選擇操作，更新種群。

步驟3對步驟2所產生子代種群執行基因編輯技術操作，更新種群。

步驟4判斷是否達到最大迭代次數maxgen，若是，則輸出適應度值最好的解作為最終優化結果，否則，轉至步驟2繼續迭代搜索。

GEDE算法的流程圖如圖5所示。

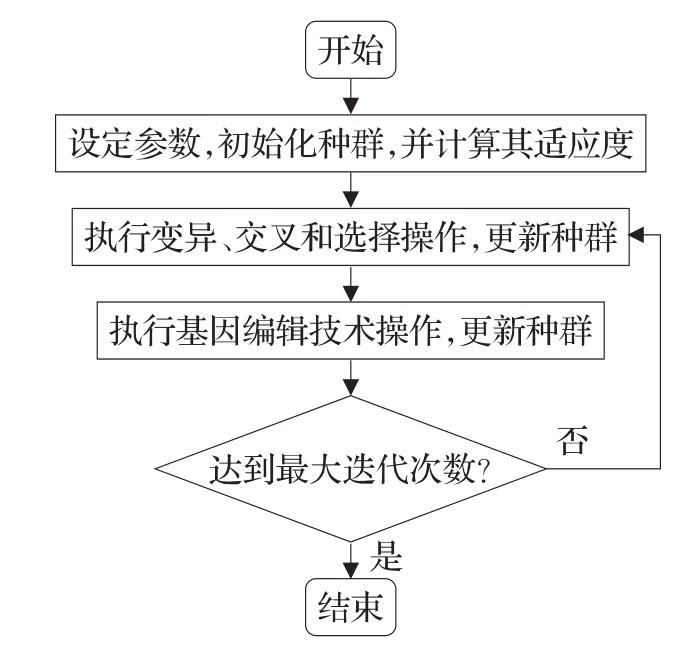
圖5 GEDE算法流程圖

5 GEDE算法在計及閥點效應的多燃料經濟調度中的應用

應用GEDE算法解決計及閥點效應的多燃料經濟調度優化問題的實現過程如下：

（1）初始化

設置種群（細胞核）大小M、最大迭代次數maxgen、交叉概率 pDE、編輯概率 pc，并根據式（12）在解空間中隨機生成初始種群。

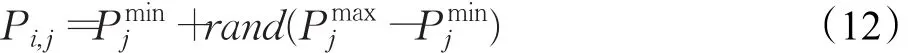
式中i∈(1,M)，j∈(1,N)。

種群中每個個體表示一個解，針對包含D臺發電機組的計及閥點效應的多燃料經濟調度優化問題，其第i個個體可表示：

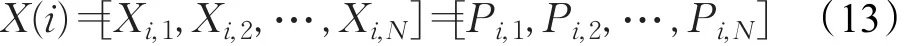
式中，X(i)為種群中第i個個體；Xi,1為個體i中第一個控制變量；Pi,1為個體i第1臺發電機組的出力。

（2）計算個體適應度

在計算個體適應度前，首先根據式（14）進行約束越限處理：

對調整后的個體，由式（15）計算其適應度值：

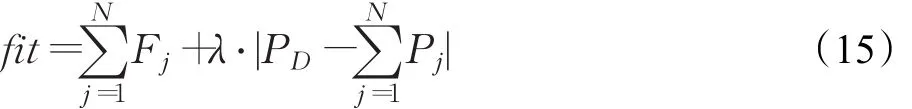
（3）執行變異、交叉及選擇操作

根據式（6）～（7）執行變異、交叉操作產生試驗個體，并由式（14）進行違約處理，隨后根據式（15）計算試驗個體的適應度，其次由式（8）進行選擇操作，只有適應度值更好的個體能保留下來，參與基因編輯技術操作。

（4）執行基因編輯技術操作

細胞核（種群）中染色體（個體）所有基因（維），進行隨機兩兩不重復配對，并依據編輯概率 pc判斷配對基因是否執行基因編輯技術操作，若執行，則由式（9）～（11）執行基因編輯技術操作中的基因定點剪切、供體重組、基因供體隨機剪切、定點基因片段替換和基因檢測

看出當該項趨于0時，與鑒定，產生新的染色體（個體）基因對，其次，由式（15）計算所有基因編輯操作后所產生新染色體的適應度，同理，根據式（8）執行選擇操作，擇優保留適應度值較好的染色體進入下一次迭代。

（5）停止條件

判斷是否達到最大迭代次數maxgen，若否，則轉至（3）執行執行變異、交叉及選擇操作，繼續迭代，若達到最大迭代次數，則輸出適應度最好的值所對應的解作為最終優化結果。

6 算例分析

6.1 算例描述及算法參數設置

為驗證本文所提GEDE算法求解具有高維、非凸、非線性、不連續特性的計及閥點效應和多燃料經濟調度優化問題的有效性與優越性，本文分別采用經典10機組及40機組的計及閥點效應和多燃料電力系統經濟調度算例進行仿真分析。其中40機組為10機組電力系統擴大4倍，相應負荷需求也擴大4倍，10機組系統具體參數見文獻[30]。10機組算例種群規模設置為100，迭代次數設為300，懲罰系數λ=0.53，交叉概率 pDE設為0.4，編輯概率 pc設為0.5。同時，為保證仿真結果的公正與合理，40機組仿真中，DE算法和GEDE算法均采用相同初始種群及算法最優參數設置，大量實驗表明，40機組系統最優交叉概率為0.3，其次該迭代次數設為2 000，其余設置與10機組相同。求解時采用MATLAB R2010 b進行程序語言編寫；計算機運行環境為Inter?CPU G5400、2.49 GHz、內存為3.40 GB，操作系統為Windows XP Professional。

6.2 優化結果分析

通過前面所述GEDE優化算法，對10機組系統和40機組系統的計及閥點效應的多燃料經濟調度算例進行優化求解，可得表1、2優化結果、表3、4分別列舉了GEDE算法應用于10機組及40機組系統獨立運行100次所得最優解的最小值、平均值、最大值及CUP平均運行時間并分別與其他各種算法的優化結果進行對比，圖6、7分別描繪了不同算法應用在兩個系統時的收斂曲線。由表1、2及文獻[30]所給出的機組參數可以看出，無論是各機組的出力還是系統總出力均分別嚴格滿足機組出力限制和系統功率平衡約束，這種優化結果表明了前面所述的約束處理方法能有效處理各種復雜的計及閥點效應的多燃料經濟調度安全運行約束問題，同時不至于干擾GEDE算法本身所固有的動態進化過程。由表3、4不難發現，在10機組測試系統中，采用GEDE算法取得的最小燃料費用為623.822 33$/h，平均費用為623.822 7$/h，最大費用為623.839 5$/h，標準差為0.037 1，CPU平均運行時間為4.74 s。雖然，GEDE算法引入基因編輯技術操作使得平均CPU運行時間相比于GE算法增加了3.33 s。然而，由圖6收斂曲線可見，GEDE算

表1 10系統機組出力、燃料類型及總出力

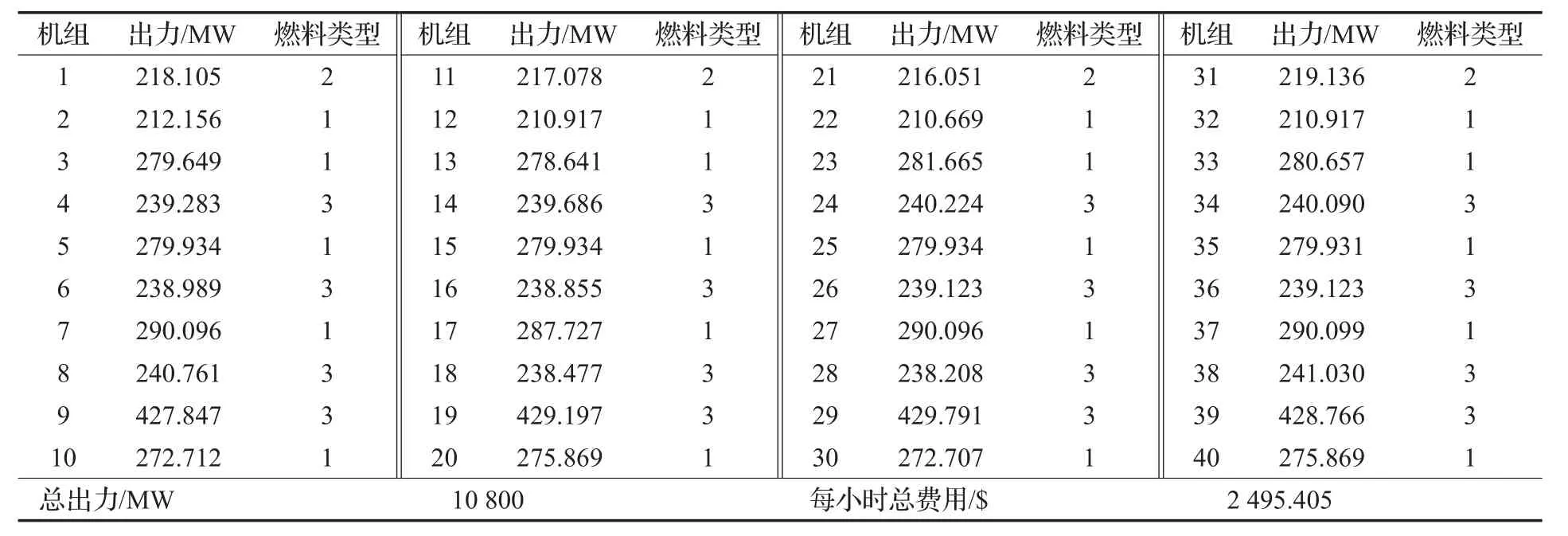
表2 40機組系統出力、燃料類型、總出力和總費用

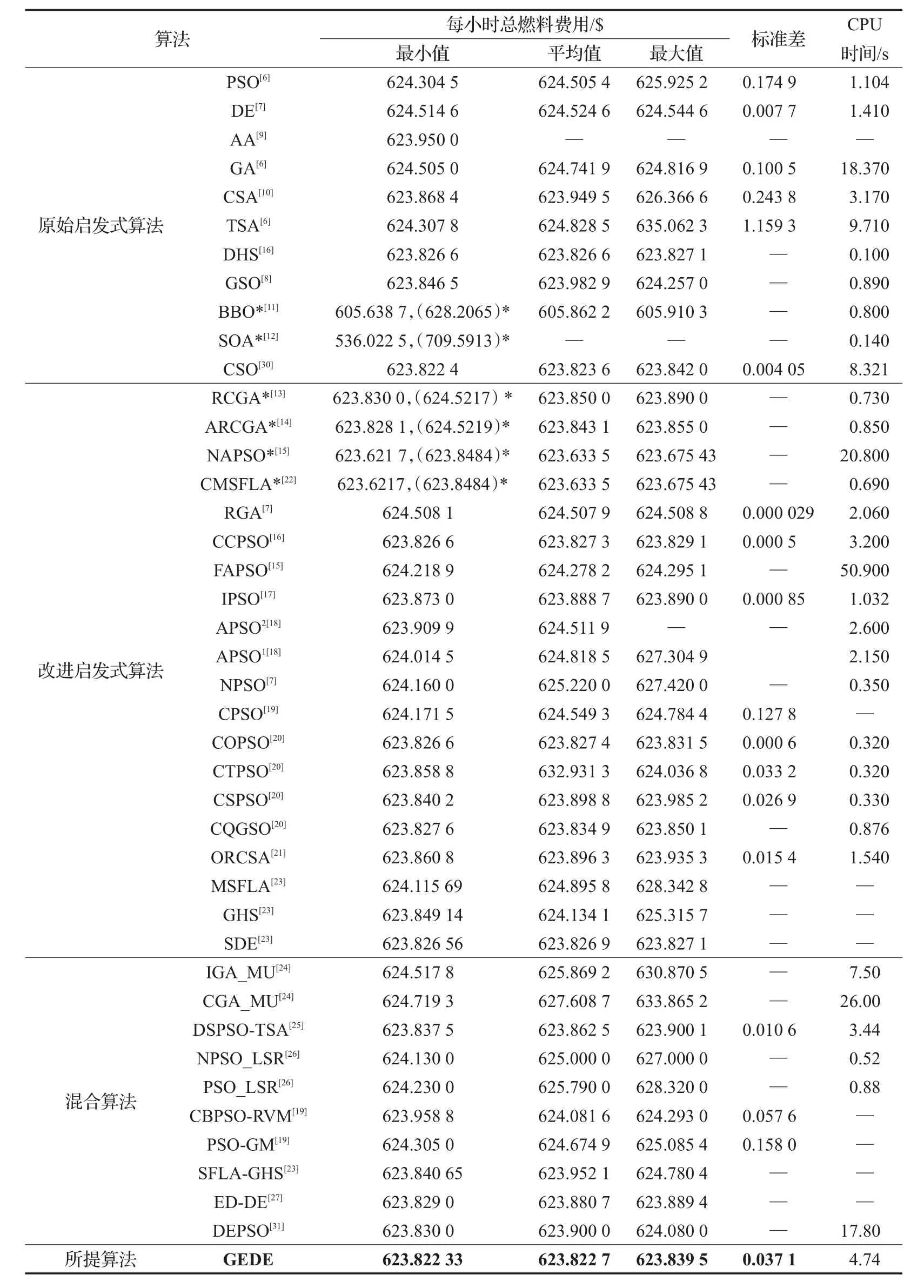
表3 10機組系統不同算法優化結果對比

法僅需148次迭代便收斂至比其他啟發式算法更優的解。因此，與DE算法及其他算法相比，GEDE算法在求解計及閥點效應的多燃料經濟調度優化問題時能在相對合理的時間內取得更優的解，并能有效避免出現過早收斂現象，可見算法具有較強的全局收斂性。同時，由表3結合文獻[30]對表3中帶*號算法最優解的糾正，不難發現，GEDE算法所取得的優化結果無論是對比于表中所列舉的原始啟發式算法、改進啟發式算法還是混合啟發式算法均具有明顯的優勢，甚至GEDE算法的最大值比諸如 PSO[25]、DE[19]、AA[9]、GA[6]、RCGA[13]、ARCGA[14]、IGA_MU[24]等32種算法所得最小費用還小。由表4可以看出，與DE算法相比，GEDE算法在相同初始種群、種群大小和迭代次數下，不管是最小值，平均值、最大值還是標準差均取得明顯優勢。顯然，GEDE算法的優化結果在40機組系統中較其他算法同樣保持明顯優勢。這一系列優勢表明GEDE算法具有較好的適應性、魯棒性和全局收斂性。

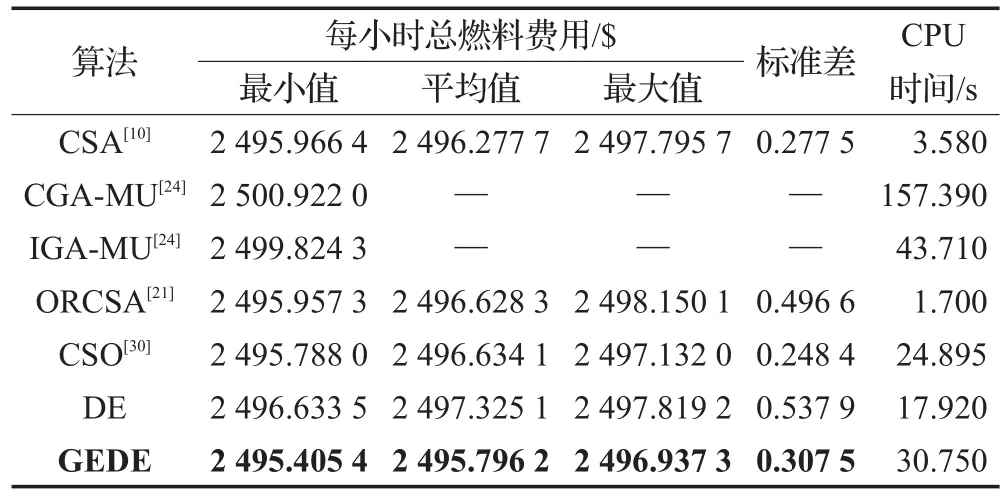
表4 40機組不同算法優化結果對比

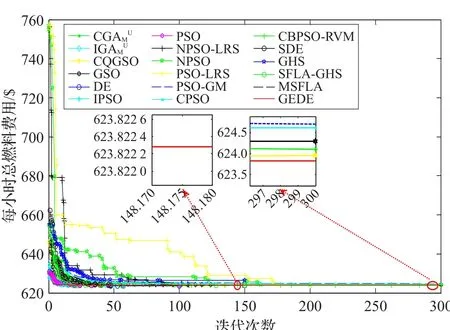
圖6 10機組系統不同算法收斂曲線對比

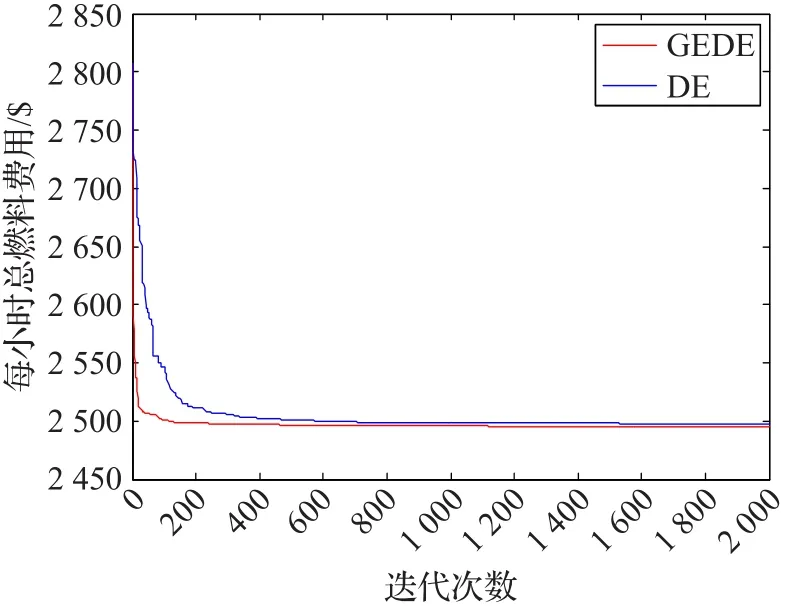
圖7 40機組DE算法與GEDE算法收斂曲線對比

7 結束語

本文針對DE算法自身所固有的計算效率低，容易陷入局部最優等缺陷，提出一種基因編輯差分算法，并將其應用于計及閥點效應的多燃料經濟調度問題經典的10機組系統和40機組系統中，驗證該算法的有效性與優越性。本文所提算法的顯著優越性在于：

（1）針對差分算法優化過程中可能出現的各決策變量違約問題，在計算適應度前提前進行違約處理，減少不可行解，提高計算可行性。

（2）隨著迭代的深入，當出現個體所有決策變量之和滿足等式約束時，此時每次基因編輯技術操作均在可行域中搜索全局最優解，這極大地提高了計算效率。

（3）采用編輯概率控制參與基因編輯操作的基因規模，在協助陷入局部維最優的部分維擺脫當前困局的同時，避免破壞正常維，有效地緩解了算法的過早熟現象。

（4）10機組和40機組系統算例驗證了所提GEDE算法，結果表明GEDE算法具有較強的適應性、魯棒性和全局收斂性。