基于全矢EMD的低速重載軸承復合故障診斷方法

韓嘉華，閻文，曹進華

（軍械工程學院 火炮工程系，石家莊 050003）

低速重載軸承通常應用于采煤機、起重機等大型機械設備，作為核心部件，其運行狀況直接影響整臺設備的性能。在機械設備的運轉過程中，轉速、承載變化以及不同故障類型的沖擊都會產生不同特點的振動信號。如何分析此類軸承故障信號的特點，提取反映故障類型的特征參量，進行軸承故障診斷具有一定的現實意義。

對于軸承故障診斷領域，小波分解的理論和應用都比較成熟，但其最大缺陷就是缺乏自適應性，主要是由于其在分解時采用的是固定的小波基函數和分解尺度［1］；Wigner-Ville分布具有高的時頻分辨率，滿足時頻邊緣特性等，但存在交叉干擾性問題需進一步完善的缺點［2-3］；局域均值分解（LMD）具有迭代次數少、瞬時頻率無副頻率等優點，但存在端點效應缺陷，導致分解所得信號兩端出現擺動、失真現象，無法有效提取故障特征［4-5］。

經驗模態分解（Empirical Mode Decomposition，EMD）是一種非平穩信號處理方法［6-10］，可以將信號局部時變特征分解成若干個IMF之和，降低了信號間特征信息的耦合，可以更加深入地分析原始數據的特征信息，有利于準確提取故障信息特征。針對低速重載軸承的故障信號，單通道所采集的信號往往不太完整，對一些故障特征較弱的信號存在遺漏。因此，采用雙通道全矢譜技術［11-12］采集信號，以保證采樣信號的完整性，得到更加準確的診斷結果。

1 基于全矢EMD的故障診斷方法

1.1 全矢譜分析方法

定義旋轉機械橢圓軌跡長半軸為該諧波下的主振矢，用RL表示，橢圓軌跡短半軸為該諧波下的副振矢，用RS表示；主振矢與x軸之間的夾角為α；軸心沿橢圓軌跡運動時的相位角為?。

假定｛xn｝和｛yn｝（n＝0，1，…，N-1）分別為x，y方向上的離散序列，其Fourier變換分別為｛Xk｝，｛Yk｝（k＝0，1，…，N-1），用序列｛xn｝，｛yn｝構成的復序列｛zn｝為

對其做Fourier變換，可以得到｛zn｝的離散Fourier變換｛ZK｝（K＝0，1，…，-1），利用Fourier變換的性質可得

進一步推導可得

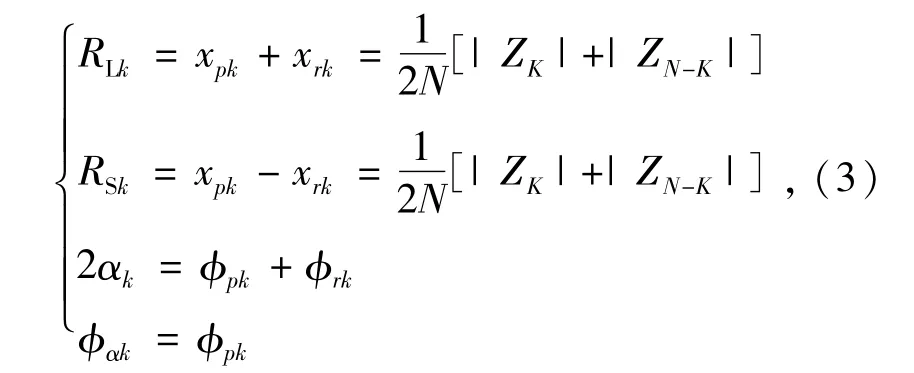
式中：RLk為主振矢；RSk為副振矢；αk為夾角；?αk為相位角。通過上述算法即可實現對雙通道數據序列進行1次Fourier變換就得到全矢譜需要的各諧波軌跡的特征信息。

1.2 EMD 算法

EMD方法通過產生一系列具有不同特征尺度的本征模態分量（IMF），將信號中不同特征尺度的沖擊或趨勢逐層分離，其具體步驟如下：

1）首先求出原始信號x（t）的所有局部極大值點和局部極小值點，采用三次樣條函數進行插值運算，形成上下包絡線，求出該上下包絡線的平均值，記為m1，并求出

高原肺水腫治療藥物的超適應證用藥現狀分析…………………………………………………… 劉可欣等（7）：995

2）根據IMF的2個特征條件判斷h1是否滿足。如果滿足，則h1作為第1個IMF；如果不滿足，則需把h1作為新的x（t），重復步驟1，直到所得h1（k－1）－m1k ＝h1k滿足以上2個特征為止。

3）從原始信號x（t）分解出第1個IMF之后，將c1從x（t）中分離出來，得到

將r1作為原始數據重復上述步驟，得到原始信號x（t）的第2個IMF，隨后再重復循環，求出r1，r2，…，rn，直到rn成為一個單調函數或rn很小時結束循環。通過以上步驟，原始信號x（t）分解為若干個IMF和一個余項之和

cj包含了原始信號x（t）從高到低的不同頻段的成分，余項rn代表原始信號x（t）的中心趨勢。

1.3 故障診斷流程

當低速重載軸承發生故障時，存在故障信號頻率低、多種故障共存、單通道情況下復合故障難分離和診斷的問題。因此，將EMD與全矢譜技術相結合的方法進行故障信號處理，其計算流程（圖1）如下：

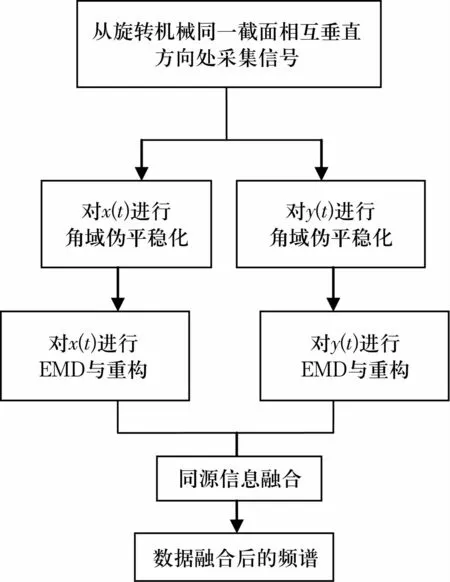
圖1 全矢經驗模態分解分析流程圖Fig.1 Analytical flow chart of full vector EMD

1）分別對同源雙通道信號x（t），y（t）進行插值重采樣，轉換為角域偽平穩信號；

3）將重構信號作為全矢譜同源信息進行融合；

4）對融合信號進行頻譜分析，提取故障特征頻率。

2 試驗驗證

2.1 試驗環境

針對低速重載軸承的使用場合，搭建如圖2所示的試驗臺，依據承載情況及機械設計標準，試驗臺上、中部采用調心滾子軸承，型號分別為22210和22217，用于承受徑向載荷；下部采用29318型推力調心滾子，用于承受軸向載荷。各軸承的具體參數見表1。

圖2 低速重載軸承試驗臺Fig.2 Test bench for bearing under low speed and heavy load

表1 試驗軸承的主要參數Tab.1 Main parameters of test bearing

在徑向加載3 500 N，1 r／min的條件下運轉60 s，采樣頻率設置為1 kHz進行軸承振動信號的采集。在上、下部軸承外圈加工深3 mm、寬2 mm的矩形槽模擬裂紋故障（圖3）。計算可得上、下部軸承的外圈故障特征頻率分別為9.6，26.7 Hz。

圖3 軸承外圈的故障部位Fig.3 Fault position of bearing outer ring

2.2 故障診斷

在相互垂直的截面上分別采集2個通道信號，運用樣條插值算法進行角域重采樣獲得角域偽平穩化信號，然后采用EMD對角域信號進行分解得到不同特征尺度的IMF，根據相關性最大化原則選擇IMF重構信號并進行頻譜分析，結果如圖4所示。從圖中可以看出試驗臺上、下部軸承外圈的故障特征頻率及其倍頻，但只能簡單判別單套軸承是否存在故障，說明僅采集1個方向的信號會有所遺漏，對軸承的故障診斷具有一定的片面性。

圖4 單通道信號的頻譜分析Fig.4 Spectrum analysis of single channel signal

將雙通道信號進行特征信息融合，對融合后的信號進行EMD處理，分解得到的各IMF如圖5所示，各IMF與原始信號的相關性見表2。

圖5 融合后信號經驗模態分解Fig.5 EMD of fused signal

表2 IMF與原始信號的相關性Tab.2 Correlation between of IMF and original signal

根據相關性最大化原則，選取IMF1，IMF2和IMF3進行信號重構，重構信號的角域重采樣及頻譜分析結果如圖6所示。從圖中可以看出：頻譜圖上顯示出一組X序列值，X1，X4，X6為上部軸承外圈故障特征頻率及其倍頻，X2，X3，X5，X8為下部軸承故障特征及其倍頻；從圖中可以得到完整的故障特征頻率分布，從而可以判斷試驗臺的上、下部軸承均存在外圈故障，避免了單通道進行故障信號分析造成的信號遺漏，提高了低速重載軸承故障診斷的準確性。

圖6 融合后信號頻譜分析Fig.6 Spectrum analysis of fused signal

3 結束語

針對低速重載軸承故障信號特點，提出了基于全矢角域和EMD的方法進行信號的故障診斷，并搭建了相應的試驗臺進行軸承復合故障振動測試。試驗結果表明全矢譜與EMD相結合的方法能夠較好地分析出復合故障。