高速鐵路單列車動(dòng)態(tài)定價(jià)與票額分配綜合優(yōu)化研究

宋文波， 趙 鵬， 李 博

(北京交通大學(xué) 交通運(yùn)輸學(xué)院， 北京 100044)

隨著高速鐵路市場(chǎng)化運(yùn)營(yíng)的發(fā)展，高速鐵路收益問(wèn)題越來(lái)越受到鐵路管理部門的重視，如何在既有固定的運(yùn)輸能力下提高收益是重要的決策問(wèn)題。高速鐵路旅客運(yùn)輸存在產(chǎn)品易逝性、預(yù)售期有限、固定成本高、邊際成本低等特點(diǎn)，適合利用收益管理的理論來(lái)提高收益。動(dòng)態(tài)定價(jià)和票額分配是高速鐵路實(shí)施收益管理的重要手段，對(duì)提高高速鐵路收益具有重要作用。目前國(guó)家發(fā)改委已經(jīng)發(fā)布了《關(guān)于改革完善高鐵動(dòng)車組旅客票價(jià)政策的通知》，逐步將高鐵票價(jià)制定權(quán)下放給中國(guó)鐵路總公司，在此背景下研究高速鐵路的動(dòng)態(tài)定價(jià)和票額分配具有重要的理論價(jià)值和實(shí)際意義。準(zhǔn)確的需求預(yù)測(cè)是實(shí)施動(dòng)態(tài)定價(jià)和票額分配的關(guān)鍵，然而需求具有隨機(jī)性和時(shí)變性，很難準(zhǔn)確預(yù)測(cè)，因此，如何在不確定需求條件下進(jìn)行動(dòng)態(tài)定價(jià)和票額分配是本文所要研究的問(wèn)題。

收益管理起源于20世紀(jì)70年代美國(guó)航空業(yè)，并得到了廣泛應(yīng)用，美國(guó)、法國(guó)、德國(guó)等鐵路公司采用收益管理，取得了顯著成效。對(duì)于收益管理問(wèn)題，國(guó)內(nèi)外的學(xué)者已經(jīng)做了深入的研究[1-16]。動(dòng)態(tài)定價(jià)方面，文獻(xiàn)[1-2]運(yùn)用強(qiáng)度控制理論研究了連續(xù)時(shí)間的單一易逝品動(dòng)態(tài)定價(jià)問(wèn)題，并將其擴(kuò)展到多產(chǎn)品動(dòng)態(tài)定價(jià)問(wèn)題。文獻(xiàn)[3]研究了顧客到達(dá)為非齊次泊松過(guò)程下的動(dòng)態(tài)定價(jià)問(wèn)題。文獻(xiàn)[4]在需求是價(jià)格的線性函數(shù)的條件下，利用最優(yōu)控制理論研究收益管理系統(tǒng)的動(dòng)態(tài)定價(jià)問(wèn)題。文獻(xiàn)[1-4]研究中，價(jià)格隨時(shí)間的變化是連續(xù)的，然而現(xiàn)實(shí)生活中價(jià)格的改變是有限的。因此，文獻(xiàn)[5-6]研究了離散價(jià)格集的連續(xù)時(shí)間動(dòng)態(tài)定價(jià)問(wèn)題。文獻(xiàn)[7-8]對(duì)我國(guó)鐵路利用動(dòng)態(tài)票價(jià)進(jìn)行了理論探討。文獻(xiàn)[9-11]研究了需求不確定條件下的易逝品的魯棒動(dòng)態(tài)定價(jià)模型。以上對(duì)于動(dòng)態(tài)定價(jià)的研究主要以理論研究為主，并且集中在一般易逝性產(chǎn)品和集裝箱班輪運(yùn)輸，在高速鐵路旅客運(yùn)輸領(lǐng)域研究較少。票額分配方面，文獻(xiàn)[12]研究了鐵路收益管理非嵌套席位控制問(wèn)題，給出了確定線性規(guī)劃模型和隨機(jī)非線性規(guī)劃模型和求解算法。文獻(xiàn)[13]研究了兩等級(jí)票價(jià)的席位控制問(wèn)題，并設(shè)計(jì)了粒子群智能算法對(duì)問(wèn)題進(jìn)行快速求解。文獻(xiàn)[14-15]研究了我國(guó)鐵路隨機(jī)需求條件下的單列車票額分配方法和嵌套式票額分配方法。文獻(xiàn)[16]以人公里數(shù)最大為目標(biāo)，通過(guò)構(gòu)建基于客車開(kāi)行方案的換乘網(wǎng)絡(luò)來(lái)進(jìn)行票額分配。但是，既有的對(duì)高速鐵路收益管理的研究中，主要集中在對(duì)票額分配的研究[12-16]，通常不考慮價(jià)格對(duì)需求的影響，然而價(jià)格對(duì)需求具有調(diào)節(jié)作用。在進(jìn)行票額分配時(shí)，文獻(xiàn)[12-16]通常假設(shè)各OD間的需求服從某種分布函數(shù)，這樣得到的優(yōu)化方案很大程度上取決于需求分布估計(jì)的準(zhǔn)確性，一旦需求估計(jì)出現(xiàn)偏差，得到的方案可能達(dá)不到收益最大化的目的。高速鐵路客票動(dòng)態(tài)定價(jià)方面的研究才剛起步，目前主要處于理論探索階段，且一般將其與票額分配獨(dú)立開(kāi)來(lái)進(jìn)行研究。然而在實(shí)際工作中高速鐵路動(dòng)態(tài)定價(jià)與票額分配是一個(gè)相互聯(lián)系不可分割的整體，票價(jià)的改變會(huì)對(duì)需求產(chǎn)生影響，從而影響票額分配。

根據(jù)對(duì)既有研究情況的分析，本文針對(duì)需求的不確定性以及目前票額分配模型不能滿足需求波動(dòng)的問(wèn)題，以收益最大化為目標(biāo)，建立高速鐵路動(dòng)態(tài)定價(jià)與票額分配穩(wěn)健優(yōu)化模型，并運(yùn)用穩(wěn)健優(yōu)化方法求解，根據(jù)客票預(yù)售期內(nèi)每個(gè)時(shí)間段每個(gè)OD客流需求的特點(diǎn)，為其制定價(jià)格并分配相應(yīng)的票額。最后通過(guò)具體的案例來(lái)驗(yàn)證模型的準(zhǔn)確性。所建的模型能夠適應(yīng)需求在一定范圍內(nèi)的波動(dòng)，防止實(shí)際需求與票額分配時(shí)的需求相差較大，使得產(chǎn)生的票額分配方案不可行，給現(xiàn)場(chǎng)帶來(lái)大量的票額調(diào)整工作。

1 模型構(gòu)建

1.1 問(wèn)題分析

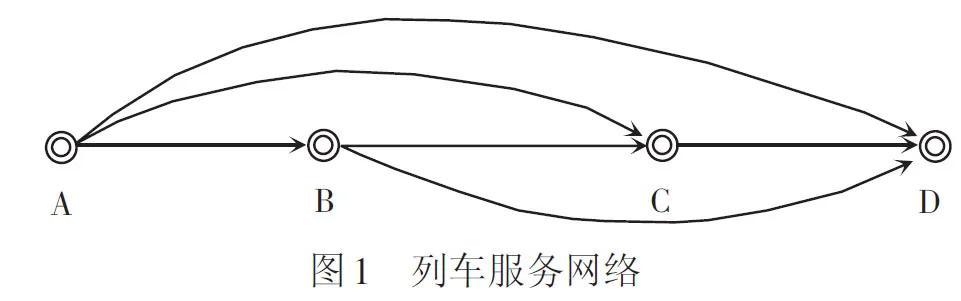
高速鐵路列車開(kāi)行方案規(guī)定了列車的運(yùn)行區(qū)段、種類及開(kāi)行對(duì)數(shù)。列車的開(kāi)行方案確定之后，其停站方案也隨之確定。列車的停站方案構(gòu)成了一個(gè)具有多區(qū)段、多OD的列車服務(wù)網(wǎng)絡(luò)。圖1所示為一列車的服務(wù)網(wǎng)絡(luò)，A為始發(fā)站，D為終到站，B、C為列車的中間停靠站，則此列車服務(wù)于AB、BC、CD 3個(gè)區(qū)段，承擔(dān)AB、BC、CD、AC、AD、BD這6個(gè)OD間的客流。票額分配的目的是根據(jù)客流特點(diǎn)將列車的運(yùn)輸能力分配到這6個(gè)OD上，使獲得的收益最大。在不考慮超員的情況下，列車在每個(gè)區(qū)段上的最大運(yùn)輸能力就是列車的定員。本文研究的問(wèn)題就是將客票的預(yù)售過(guò)程分為T個(gè)時(shí)期，根據(jù)每個(gè)時(shí)期t(t=1,2,…,T)內(nèi)各OD間客流與票價(jià)的關(guān)系，為各OD制定價(jià)格，并為各OD分配相應(yīng)的票額。本文不考慮運(yùn)行線路上列車之間的相互影響和列車超員。

1.2 數(shù)學(xué)模型

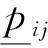
xijt表示第t時(shí)段OD對(duì)(i,j)的票額需求，該需求是不確定的，但是它隨價(jià)格變化的模式是可以預(yù)測(cè)的，其為價(jià)格pijt的函數(shù)，xijt=xijt(pijt)。根據(jù)文獻(xiàn)[9]，假設(shè)隨機(jī)需求的形式為線性函數(shù)和隨機(jī)誤差組合而成，即

xijt=αijt-βijt·pijt+εijtt=1,2,…,T

( 1 )

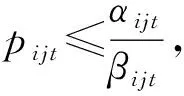
在既有固定的運(yùn)輸能力下，需求不確定條件下的高速鐵路動(dòng)態(tài)定價(jià)與票額分配綜合優(yōu)化模型(M1)為

( 2 )

s.t.

?t,?(i,j)∈FL=1,2,…,m-1

( 3 )

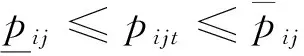
( 4 )

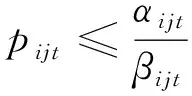
( 5 )

若lek>lij，則

pekt>pijt?t,?(e,k),(i,j)∈F

( 6 )

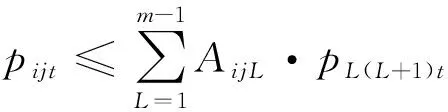
( 7 )

若Ω={L|(i,j)∈F且AijL=1}，則

?t,?g∈Ω

( 8 )

pijt∈N

( 9 )

式中：(e,k)為從i站到j(luò)站的OD對(duì)；Ω為組成OD對(duì)(i,j)的各區(qū)段集合；N為非負(fù)整數(shù)集。

式( 2 )是模型的目標(biāo)函數(shù)，通過(guò)確定所有OD在預(yù)售期內(nèi)的每個(gè)時(shí)段的票價(jià)和相應(yīng)的票額，使得鐵路運(yùn)輸收益最大。式( 3 )是能力約束，所有OD對(duì)(i,j)在任一區(qū)段上累積的票額需求之和不得超過(guò)列車在該區(qū)段的最大運(yùn)輸能力。式( 4 )表示預(yù)售期內(nèi)每個(gè)時(shí)段各OD的票價(jià)不得低于一個(gè)票價(jià)下限，防止鐵路票價(jià)過(guò)低造成收益損失，同時(shí)考慮到鐵路運(yùn)輸?shù)纳鐣?huì)公益服務(wù)特性，票價(jià)不能高于一個(gè)票價(jià)上限，防止運(yùn)輸能力緊張時(shí)期(如春節(jié)、五一等)票價(jià)過(guò)高，造成社會(huì)不良影響。式( 5 )表示每個(gè)時(shí)段票額需求不能為負(fù)數(shù)。式( 6 )表示在預(yù)售期的同一時(shí)間段內(nèi)OD距離越長(zhǎng)，票價(jià)越高。式( 7 )表示在預(yù)售期的同一時(shí)間段內(nèi)票價(jià)率是遞遠(yuǎn)遞減的，則OD的票價(jià)小于組成此OD的各區(qū)段的票價(jià)之和。式( 8 )表示OD的票價(jià)應(yīng)大于組成此OD的各區(qū)段的票價(jià)之和減去任意區(qū)段的票價(jià)。式( 9 )是票價(jià)的整數(shù)約束。

2 模型求解

由于需求函數(shù)中存在隨機(jī)誤差項(xiàng)εijt，因此模型(M1)的最優(yōu)解會(huì)受到隨機(jī)誤差項(xiàng)的影響。如果不能準(zhǔn)確估計(jì)式( 1 )中隨機(jī)誤差項(xiàng)εijt的分布，則得到的最優(yōu)解可能不滿足列車運(yùn)輸能力的限制，從而達(dá)不到收益最大化的目的。實(shí)際上，為了得到穩(wěn)健最優(yōu)解(Robust Optimization)，不必滿足所有情況下的約束條件，可以在某個(gè)縮小的隨機(jī)誤差項(xiàng)變化范圍內(nèi)求得最優(yōu)解，這樣得到的解不僅能適應(yīng)隨機(jī)誤差項(xiàng)的變化，而且目標(biāo)函數(shù)的值也不至于過(guò)多地?fù)p失。為此，本文引入穩(wěn)健優(yōu)化模型方法[11]，在假設(shè)已知隨機(jī)誤差項(xiàng)εijt的變動(dòng)范圍而不知道其確切分布時(shí)，在解的穩(wěn)健性和目標(biāo)函數(shù)的最優(yōu)值之間尋求平衡，來(lái)適應(yīng)需求的不確定性。

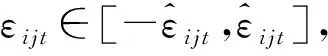
(10)

引入?yún)?shù)Δij，Δij為給定的非負(fù)實(shí)數(shù)，用來(lái)約束OD對(duì)(i,j)各時(shí)段實(shí)際總需求與名義總需求的偏離程度，則有

(11)

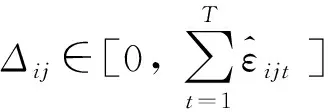
因此，考慮需求函數(shù)的不確定性，將式(10)、式(11)帶入模型(M1)中，并且在目標(biāo)函數(shù)中增加由隨機(jī)誤差引起的收入變化量的最小值達(dá)到最大的一項(xiàng)，可以將模型(M1)轉(zhuǎn)化為動(dòng)態(tài)定價(jià)穩(wěn)健模型(M2)，即

(12)

s.t.

(13)

(14)

(15)

ξijt≤1

(16)

(17)

若lek>lij，則

pekt>pijt?t,?(e,k),(i,j)∈F

(18)

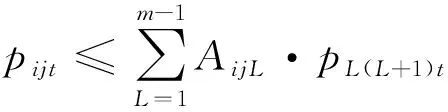
(19)

若Ω=L|(i,j)∈F且AijL=1則

?t，?g∈Ω

(20)

pijt∈N

(21)

在模型(M2)中約束條件式(13)為

約束條件式(14)為

合并約束條件式(13)和式(14)，則約束條件式(13)可以松弛為

通過(guò)變換可以將模型(M2)松弛為穩(wěn)健模型(M3)，即

(22)

s.t

(23)

ξijt≤1

(24)

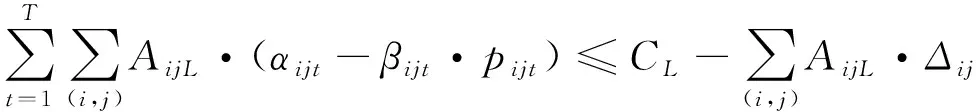
(25)

(26)

若lek>lij，則

pekt>pijt?t,?(e,k),(i,j)∈F

(27)

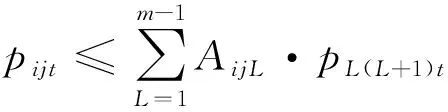
(28)

若Ω=L|(i,j)∈F且AijL=1則

?t，?g∈Ω

(29)

pijt∈N

(30)

模型(M3)為一個(gè)兩層規(guī)劃問(wèn)題，其內(nèi)層最小化問(wèn)題可以認(rèn)為是決策變量為ξijt的線性規(guī)劃，約束條件式(23)、式(24)為內(nèi)層規(guī)劃問(wèn)題的約束，通過(guò)求解內(nèi)層規(guī)劃的對(duì)偶問(wèn)題，并利用強(qiáng)對(duì)偶定理可以將模型(M3)轉(zhuǎn)化為如下凸規(guī)劃問(wèn)題模型(M4)：

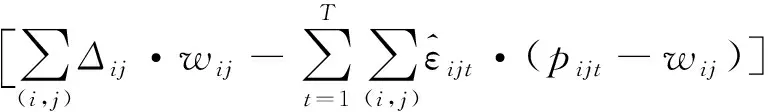
(31)

s.t.

(32)

(33)

(34)

若lek>lij，則

pekt>pijt?t,?(e,k),(i,j)∈F

(35)

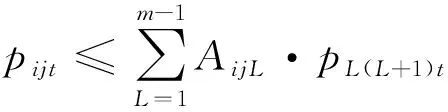
(36)

若Ω=L|(i,j)∈F且AijL=1則

?t，?g∈Ω

(37)

pijt∈N

(38)

wij≥0

(39)

在模型(M4)中，wij為模型(M3)中內(nèi)層規(guī)劃的對(duì)偶問(wèn)題的決策變量。

通過(guò)求解模型(M4)，可以得到客票預(yù)售期內(nèi)每個(gè)時(shí)段每個(gè)OD的最優(yōu)定價(jià)，繼續(xù)利用式( 1 )便可求得每個(gè)時(shí)段每個(gè)OD的票額分配結(jié)果。

3 案例分析

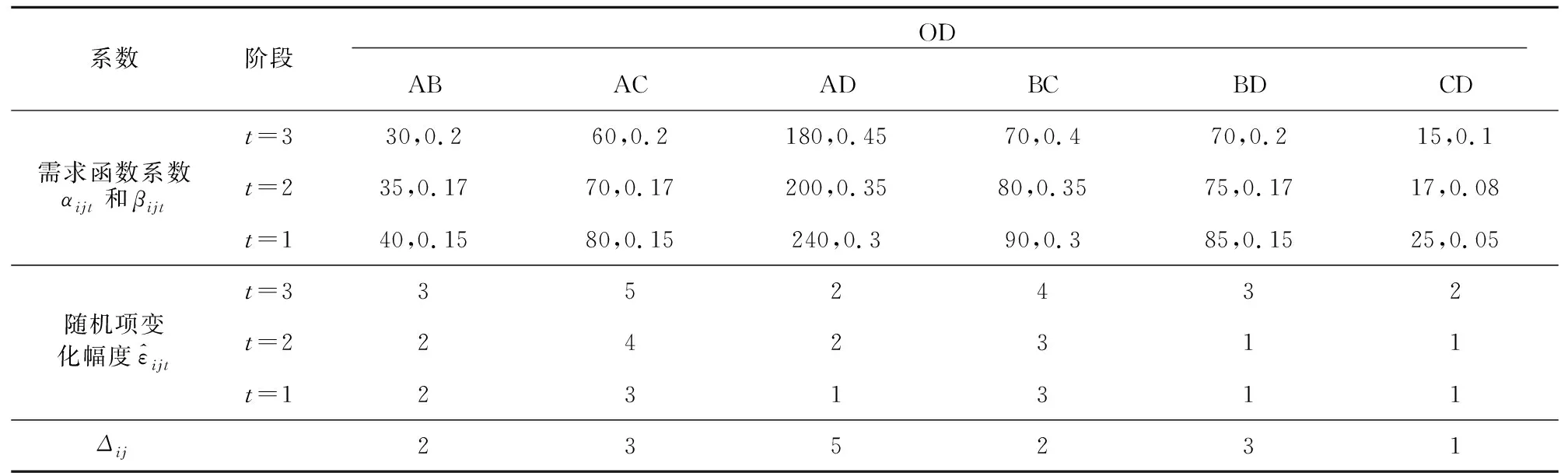
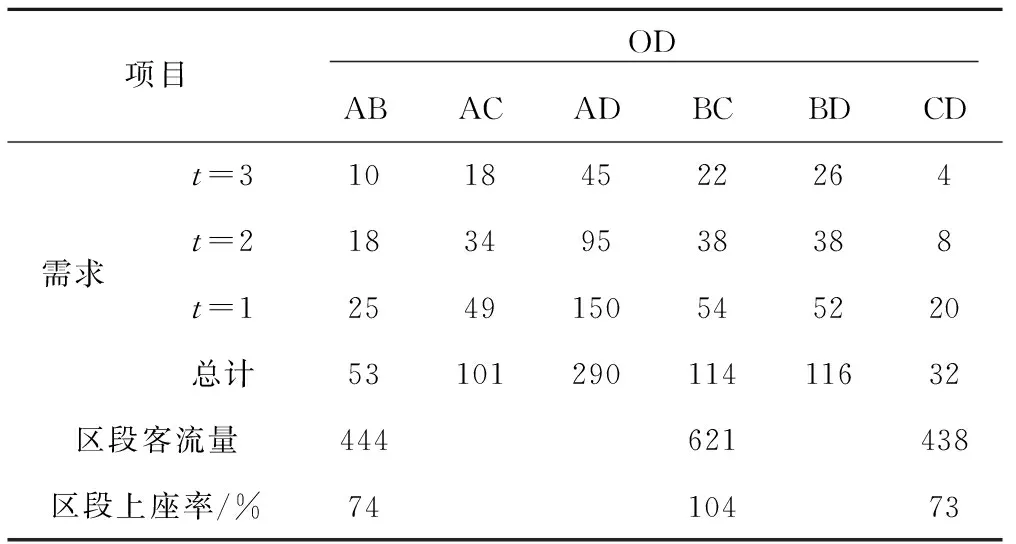
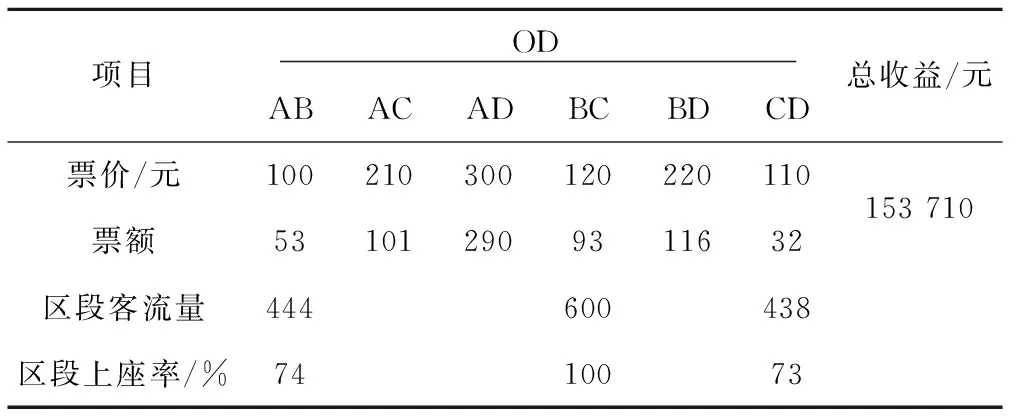
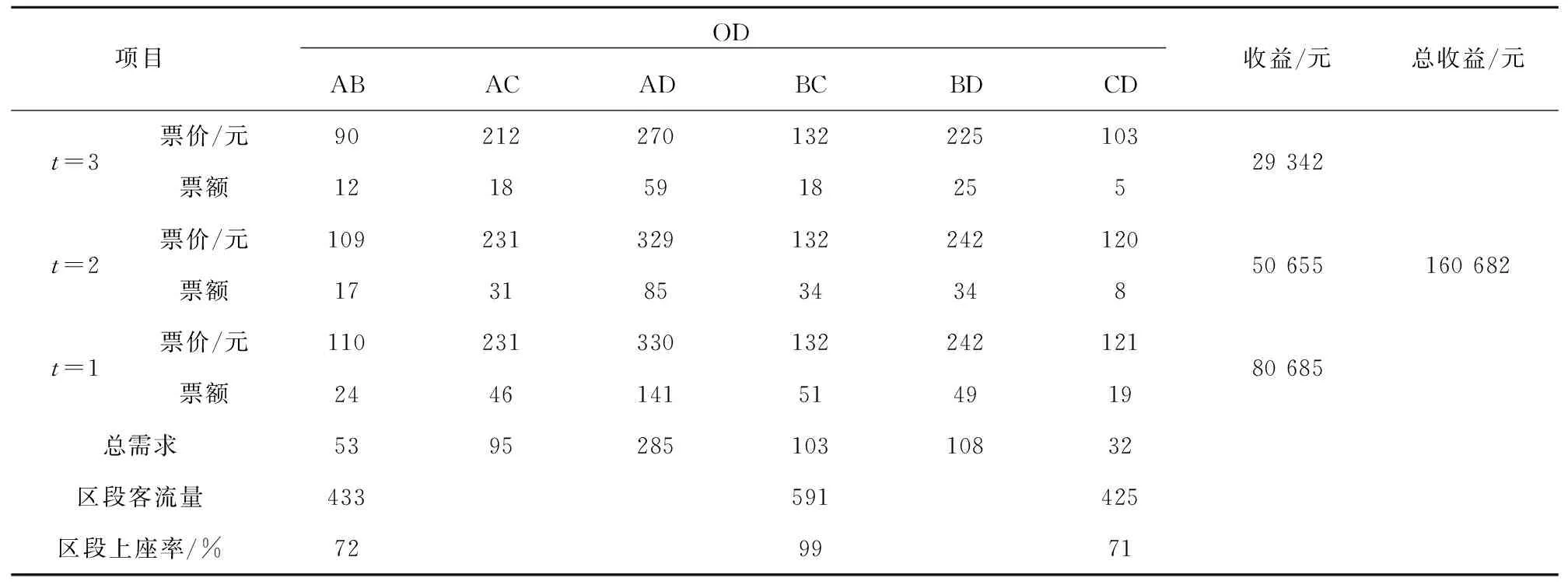
根據(jù)文獻(xiàn)[17]的數(shù)據(jù)，假設(shè)某高速列車運(yùn)行線路包含4個(gè)客運(yùn)站3個(gè)區(qū)段，見(jiàn)圖2。列車在該線路的客運(yùn)站上均有客運(yùn)作業(yè)。假設(shè)列車的定員為600人，即CL=C=600，根據(jù)《關(guān)于動(dòng)車組票價(jià)有關(guān)事項(xiàng)的通知》中的規(guī)定，目前票價(jià)可以上下浮動(dòng)10%。則各OD票價(jià)及其上下限如表1所示，各OD距離大小關(guān)系為lAB

表1 各OD票價(jià)及其上下限取值元

本文將客票預(yù)售期分為3個(gè)階段，即t=1,2,3，t越小表示越接近列車發(fā)車時(shí)間，需求函數(shù)系數(shù)αijt隨t的增大而減小，βijt隨t的增大而增加，表示越臨近發(fā)車時(shí)間，旅客需求對(duì)價(jià)格的敏感性越低，這符合收益管理思想[10]，即在售票初期(t=3)由于人們不能確定出行時(shí)間所以需求量較小，因此售票初期αijt值較小，而此時(shí)旅客的敏感性較高，因此售票初期βijt值較大，可以通過(guò)降低票價(jià)來(lái)吸引客流。

根據(jù)收益管理思想和文獻(xiàn)[17]中全價(jià)票下需求函數(shù)的關(guān)系，將客票預(yù)售期分為3個(gè)階段，給出不同售票階段各OD的需求函數(shù)系數(shù)及其隨機(jī)項(xiàng)變化幅度，并在假定鐵路管理部門掌握一定的需求信息后，給出Δij的取值，見(jiàn)表2。

表2 系數(shù)取值

如果鐵路管理部門在售票時(shí)不考慮不同售票階段旅客對(duì)價(jià)格的敏感性，在每個(gè)售票階段都以單一全價(jià)票的方式進(jìn)行客票銷售，則根據(jù)表2中不同售票階段的需求函數(shù)關(guān)系，在全價(jià)票下各OD的需求及各區(qū)段上座率見(jiàn)表3。

表3 單一全價(jià)票下各OD需求及區(qū)段客流量

表3中可以看出，在以單一全價(jià)票進(jìn)行客票銷售時(shí)，BC區(qū)段的客流需求超過(guò)了列車的定員，表明列車的運(yùn)輸能力不能滿足所有旅客的需求。利用文獻(xiàn)[14]中的票額分配模型，以收益最大化為目標(biāo)，根據(jù)全價(jià)票下各OD的客流需求，得到的票額分配方案如表4所示。利用Lingo12.0對(duì)本文所建模型(M4)進(jìn)行求解，得到的動(dòng)態(tài)定價(jià)與票額分配方案見(jiàn)表5。

表4 單一全價(jià)票下票額分配方案

表5 動(dòng)態(tài)定價(jià)和票額分配方案

對(duì)比表3和表4，可以看出在以單一全價(jià)票對(duì)客票進(jìn)行銷售時(shí)，由于票價(jià)固定，各OD間的需求是一個(gè)定值，在此需求下，根據(jù)各區(qū)段上座率可以看出，列車的運(yùn)輸能力并不能滿足所有旅客的需求，因此在以收益最大化為目的進(jìn)行票額分配時(shí)，通過(guò)減少OD對(duì)BC間的票額數(shù)來(lái)限制BC間的客流需求，使得各區(qū)段的客流量都不超過(guò)列車定員，這種方式由于限制了部分旅客的需求，可能會(huì)造成旅客滿意度的下降，此種方式下獲得的收益為153 710元。

表5是在考慮不同售票階段旅客對(duì)價(jià)格的敏感性不同，根據(jù)本文所建的模型求得的動(dòng)態(tài)定價(jià)和票額分配方案，可以看出通過(guò)調(diào)整不同售票階段的票價(jià)，各OD間的需求發(fā)生了變化，各區(qū)段的客流量都不超過(guò)列車定員。售票初期由于旅客對(duì)價(jià)格的敏感性較高，票價(jià)相對(duì)較低可以吸引一部分客流，但是分配的票額數(shù)相比開(kāi)車前分配的票額數(shù)較少，這也符合收益管理的思想，為了獲得更多的收益，把票額留給愿意支付更高價(jià)格的旅客。OD對(duì)AC、BC、BD在售票初期票價(jià)高于全價(jià)票，說(shuō)明這3個(gè)OD對(duì)間的客流需求比較旺盛。此方案下可以獲得的收益為160 682元。與表4相比，利用本文模型求得的動(dòng)態(tài)定價(jià)和票額分配方案能夠獲得更多的收益，但各區(qū)段的上座率并沒(méi)有提高，這也說(shuō)明了并不是將車票賣的越多能夠獲得的收益越大，而是將車票賣給愿意支付更高價(jià)格的旅客才能獲得更多的收益。同時(shí)，通過(guò)調(diào)整不同售票階段的票價(jià)，來(lái)調(diào)節(jié)各OD間的客流需求從而可以獲得更多的收益，相比單一全價(jià)票情況下利用分配的票額數(shù)來(lái)限制客流的需求，動(dòng)態(tài)定價(jià)方式是通過(guò)調(diào)整票價(jià)來(lái)主動(dòng)引導(dǎo)客流需求的變化，更符合旅客的心理需求。通過(guò)對(duì)比，可以看出利用本文模型計(jì)算出來(lái)的方案可以獲得更多的收益，從而驗(yàn)證了采用動(dòng)態(tài)定價(jià)相比現(xiàn)有的單一票價(jià)較優(yōu)，并且模型中考慮了需求的波動(dòng)，使得計(jì)算出來(lái)的票額分配方案能夠適應(yīng)實(shí)際需求在一定范圍內(nèi)的波動(dòng)，避免了實(shí)際需求波動(dòng)較大時(shí)，導(dǎo)致方案不可行，給現(xiàn)場(chǎng)帶來(lái)大量的票額調(diào)整工作。然而，由于目前高速鐵路動(dòng)態(tài)調(diào)整票價(jià)仍處于探索階段，需求隨票價(jià)變化的關(guān)系需要不斷地在實(shí)踐中積累，因此在運(yùn)用本文模型時(shí)需要根據(jù)實(shí)踐對(duì)需求函數(shù)及其需求波動(dòng)情況不斷地進(jìn)行改進(jìn)。

4 結(jié)束語(yǔ)

本文基于收益管理理論，對(duì)不確定需求下的高速鐵路單列車的動(dòng)態(tài)定價(jià)與票額分配方法進(jìn)行了研究，根據(jù)客票預(yù)售期不同階段客流需求的特點(diǎn)為各OD車票制定價(jià)格并分配相應(yīng)的票額，在模型中考慮了需求的波動(dòng)，使得到的方案能夠適應(yīng)實(shí)際需求的波動(dòng)，避免了實(shí)際需求波動(dòng)較大時(shí)導(dǎo)致方案不可行。通過(guò)算例，并與單一全價(jià)票下的票額分配方案對(duì)比，結(jié)果表明動(dòng)態(tài)調(diào)整票價(jià)不僅可以調(diào)節(jié)客流，還可以提高收益，從而驗(yàn)證了模型的可行性與可操作性。本研究為高速鐵路票價(jià)制定提供了一個(gè)新的方法，但僅研究了單列車的情況，此外旅客對(duì)票價(jià)的敏感性及其客流需求的波動(dòng)情況需要根據(jù)長(zhǎng)期的運(yùn)輸實(shí)踐來(lái)獲得，今后將進(jìn)一步研究多列車、多條運(yùn)輸線路及其考慮旅客選擇行為的更加符合實(shí)際情況的高速鐵路動(dòng)態(tài)定價(jià)與票額分配問(wèn)題。