面向圓盤造球機動態特性的研究與優化

晏遠志，楊金堂，王宏旭，侯作義

（1.武漢科技大學 機械自動化學院，湖北 武漢 430081；2.老河口市綠華環保科技有限公司，湖北 襄陽 441800）

1 引言

圓盤造球機是球團礦生產的重要設備，而其可靠性與穩定性又是影響球團礦質量的關鍵。在國內，由于圓盤造球機造球質量較好，因而在球團礦生產中應用較多。通過對其使用情況來看，盤體旋轉的平穩性還較差，直接影響整機的工作性能，這表明造球系統的動力學性能還有待加強。因此有必要對造球系統結構進行優化以提升其動態特性。

目前國內對圓盤造球機的研究相對較少，設計理論和方法比較單一，常規的運動學分析、靜力學分析的方法已不能滿足眼前造球機的發展需要。文獻[1]分析了圓盤造球機的基本結構，并研究了某些運動學規律；文獻[2]對圓盤造球機盤體進行了靜力學分析和輕量化設計。目前，還很少有研究人員對圓盤造球機的動態性能作出研究[3]。

以某公司的Φ1800圓盤造球機盤體及傳動部分組成的懸臂轉子系統為研究對象，利用模態分析、諧響應分析方法對其薄弱部位進行辨識[4]，識別出盤體對該轉子系統的動態性能影響最大。以盤體結構作為優化目標，利用尺寸靈敏度分析方法[5]和模糊物元法[6]對盤體進行優化，使其結構更加合理。優化之后的分析結果表明：轉子系統的前六階固有頻率都得到了提高，x、y、z三個方向最大共振峰值大幅度降低，懸臂轉子系統的動態性能取得較大改善。

2 轉子系統動態分析與優化目標確定

2.1 整機模型簡化

某公司圓盤造球機，如圖1所示。由于造球系統的主要問題是圓盤旋轉的平穩性較差，所以僅對由盤體以及支撐軸承、軸承座、傳動軸組成的懸臂轉子系統進行研究。

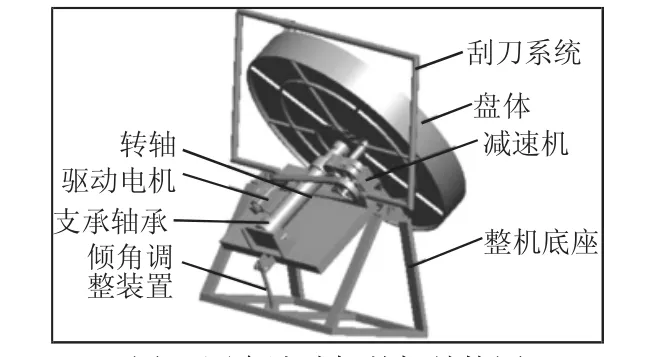
圖1 圓盤造球機整機結構圖Fig．1 Machine Diagram of Disc Pelletizer

在轉子系統中，軸承并不是絕對剛性的，會發生彈性變形，因此支承系統就等同于彈簧與轉軸串聯，對轉子系統進行有限元分析的時候，有必要對軸承進行一定的等效。在ANSYS Workbench軟件中，采用了Spring單元模擬軸承的支承作用。

2.2 滾動軸承剛度的計算

本結構支承中裝有兩個滾動軸承，由文獻[7]和軸承承受的徑向力以及造球機轉子系統的結構尺寸，求得滾動軸承的剛度K=6．2×108N/mm。由于在此工況下滾動軸承的阻尼很小，對后面進行動力學分析的影響不大，因此可以忽略[8-9]。

2.3 懸臂轉子系統動力學分析

2.3.1 模態分析

利用ANSYS Workbench對懸臂轉子系統進行模態分析，得到系統的低階固有頻率與振型情況。設置盤體材料為Q235A（密度為 7850kg/m3，彈性模量為 206GPa，泊松比為 0．3），轉軸部件為普通碳鋼（密度為7800kg/m3，彈性模量為210GPa，泊松比為0．3）。為了模擬真實工況，保留轉軸繞軸線旋轉自由度，軸承座與軸承以及軸的結合面采用彈簧單元進行等效，其余接觸部分采用綁定接觸方式。計算得到轉子系統的前六階固有頻率以及前三階振型情況，分別如表1、圖2所示。

表1 懸臂轉子系統前六階固有頻率及振型描述Tab.1 First Six Natural Frequencies and Vibration Models of the Rotor System

圖2 轉子系統前三階振型圖Fig．2 First Three Vibration Models of the Rotor System

由表1與圖2可看出，第一階固有頻率近似為0Hz，即剛體模態，可以忽略；轉子系統的低階振型都表現為以盤體結構為主的振動形式，由此可知，盤體就是對轉子系統低階振型影響程度最大的結構件。

2.3.2 諧響應分析

為了反映轉子系統在礦球激勵下的動態性能變化情況，以盤底為參考點，在盤體底面和內壁分別施加幅值為1000N和250N，頻率為（0～60）Hz的簡諧力，測得轉子系統位移頻響曲線圖，如圖3所示。

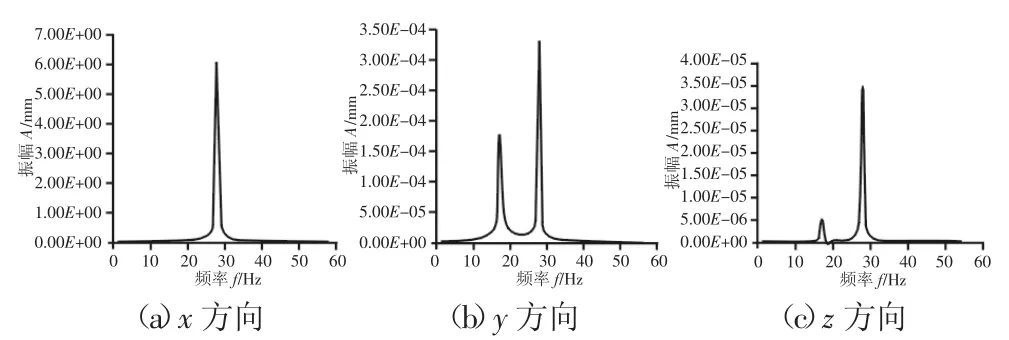
圖3 轉子系統在x、y、z三個方向的諧響應曲線Fig．3 Harmonic Response Curve of x、y、z in Three Directions of the Rotor System

從圖3可看出，轉子系統在x、y、z三個方向上的最大共振峰值均出現在28Hz，這對應于系統的第四階固有頻率。在y、z方向上，系統在17Hz即第二固有階頻率也出現了共振峰值。由于共振峰值最大的頻率點即為轉子系統的最薄弱共振點，因此系統的第四階固有頻率即對其動態性能影響最大。

2.4 轉子系統優化目標的確定

由以上分析表明，盤體結構對轉子系統的低階振型影響最大；而系統的第四階固有頻率在三個方向上對系統的動態性能影響最大。由于轉子系統結構的每階固有頻率對應一個振型，所以可判斷盤體結構為影響轉子系統動態性能的關鍵部位。通過對盤體結構進行優化設計，可避免對轉子系統動態性能優化的盲目性，提高優化效率。

3 盤體結構的優化設計

由于盤體結構尺寸較為復雜，各尺寸參數對盤體結構模態的貢獻不同，而且在結構設計中，為提高結構的固有頻率往往會增加板的厚度，這雖然會增加了剛度，但同時也增加其質量，因此先采用靈敏度分析的方法確定各尺寸參數對盤體結構的第四階固有頻率和質量的影響程度，然后對比較敏感的參數進行優化設計。

3.1 靈敏度分析

利用ANSYS Workbench中的Design Exploration下的Response Surface Optimization進行靈敏度分析，盤體的各個尺寸參數在盤體中的具體位置，如圖4所示。

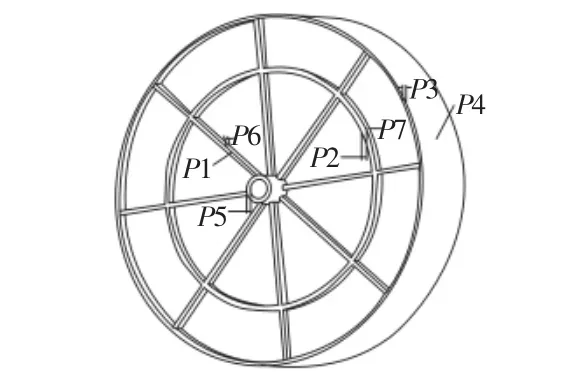
圖4 盤體尺寸位置簡圖Fig．4 Position Sketch of Disk Body Size

各待優化參數對應的參數符號、初值以及范圍，如表2所示。計算出這些分析尺寸對轉子系統的第四階固有頻率和質量的靈敏度大小，如圖5所示。

表2 選定尺寸的變化范圍Tab.2 Selected Size Range

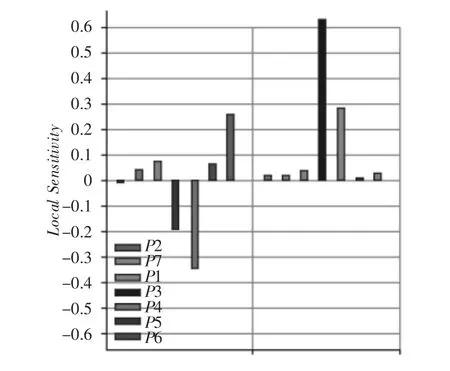
圖5 各優化變量對第四階固有頻率和質量的靈敏度Fig.5 Sensitivity about Fourth Natural Frequency and Quality of Each Optimization Variables

由圖5可知，與第四階固有頻率成反比的尺寸是：P4，P3；成正比的是：P6、P1、P5且P2、P7對第四階固有頻率幾乎無影響。對盤體質量的影響大小順序是：P3、P4、P1、P6 且 P2、P5、P7 對質量幾乎無影響。

綜合本次靈敏度分析的結果，剔除對第四階固有頻率和質量影響較小的參數，選擇P1、P3、P4、P6作為設計變量，對盤體結構進行優化。

3.2 盤體結構優化分析

根據上文分析結果，將盤體結構的第四階固有頻率和質量作為優化目標，將盤體的尺寸參數 P1、P6、P3、P4 依次設為 x1，x2，x3，x4作為優化參數。在ANSYS Workbench中的Response Surface Optimization下的Optimization優化分析模塊中經過反復優化迭代求解后得到5組候選設計點，原設計方案與優化之后的候選設計點，如表3所示。

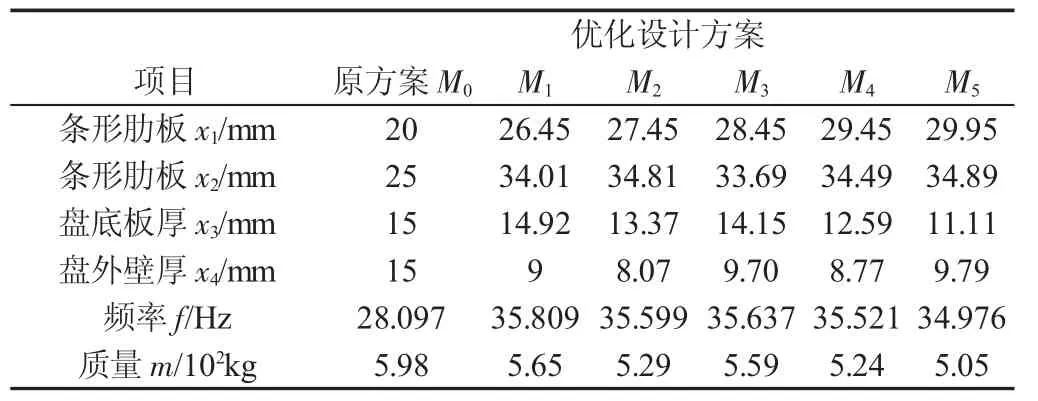
表3 優化設計結果Tab.3 Optimization Design Results

3.3 最優設計方案

盤體模態評價是一個多指標決策過程，存在單項指標評價結果的不相容性問題，因此需要借助評價方法獲取最優的設計方案。利用基于熵權的模糊物元分析法作為評價模型[10]，獲得造球機盤體的最優設計方案，其步驟如下。

3.3.1 確定模糊物元判斷矩陣R

盤體模態優化中事物M有C1，C2，…，C66個特征及其相應的量值，這些構成了5種事物的6維復合模糊物元判斷矩陣R。

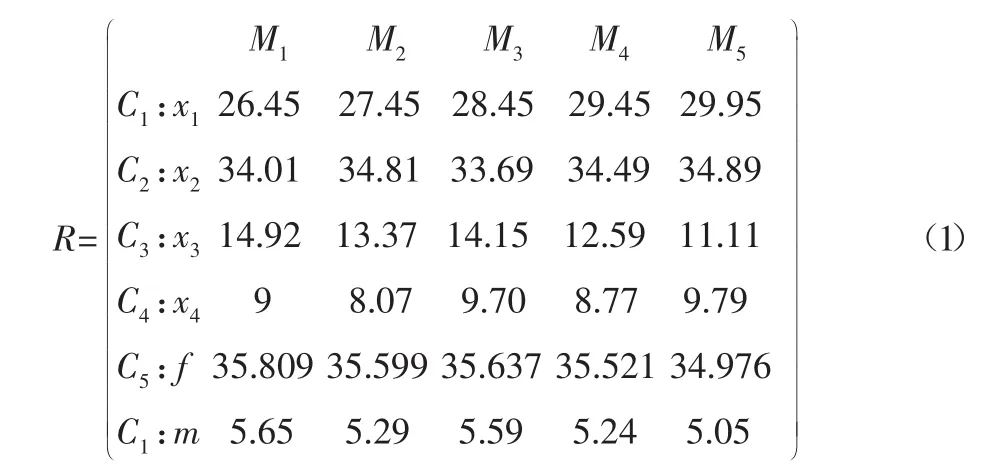
式中：Ci（i=1，…6）—特征評價指標；Mj（j=1，…，5）—各設計方案。

3.3.2 確定從優隸屬度矩陣

由于每個評價指標的特征值對于設計方案來講，有的成正比，有的成反比，所以對不一樣的從優隸屬度uij分別要利用不同的公式進行求解。

若評價指標Ci的值與頻率f成正比時，則使用效益型指標：

若評價指標Ci的值與頻率f成反比時，則使用成本型指標：

式中：xij—矩陣R中方案Mj的指標Ci所對應的屬性值。在6種指標中x1，x2和f對模態頻率來說越大越好，故選用效益型指標，其余選用成本型指標。利用上式對模糊物元判斷矩陣進行計算得到從優隸屬度uij。其中uij為從優隸屬度矩陣R~nm中對應的元素，從而得到矩陣R~nm。

3.3.3 計算評價指標的熵和權重

由于評價指標權重反映的是各指標對評估方案的影響程度，所以確定指標權重對于準確地進行評估十分的重要。則利用熵權法計算評價指標的權重。由隸屬度矩陣中n個評價指標和m個評價對象得到第i個評價指標的熵為：

計算得到評價指標的熵向量 H=（0.982，0.981，0.982，0.985，0.980）T，最后得到第i個指標的權重為：

計算得到評估指標權重向量 K=（0.1999，0.2164，0.1947，0.1625，0.2263）。盤體各優化方案的優劣由下式確定：

通過計算得到優劣性能向量 P=（0.2203，0.5966，0.3052，0.6958，0.8375），由向量P可知，盤體的優化設計方案優劣依次為：M5，M4，M2，M3，M1；因此 M5為最優設計方案。由設計方案 M5表明：該方案中轉子系統相對于原來第四階固有頻率增加了24.48%，盤體質量減小了15.55%。

4 優化結果驗證

在選擇方案M5，且相同的邊界條件下，經驗證轉子系統滿足靜剛度要求，盤體優化前后轉子系統的前六階固有頻率對比結果，如表4所示。

表4 盤體優化前后轉子系統前六階固有頻率（Hz）Tab.4 First Six Natural Frequencies of Rotor System before and after Disk Body Optimize

表4表明，優化后的懸臂轉子系統前六固有階頻率均得到了不同程度的提高。優化前后轉子系統在x、y、z方向上的位移頻響曲線，如圖6所示。

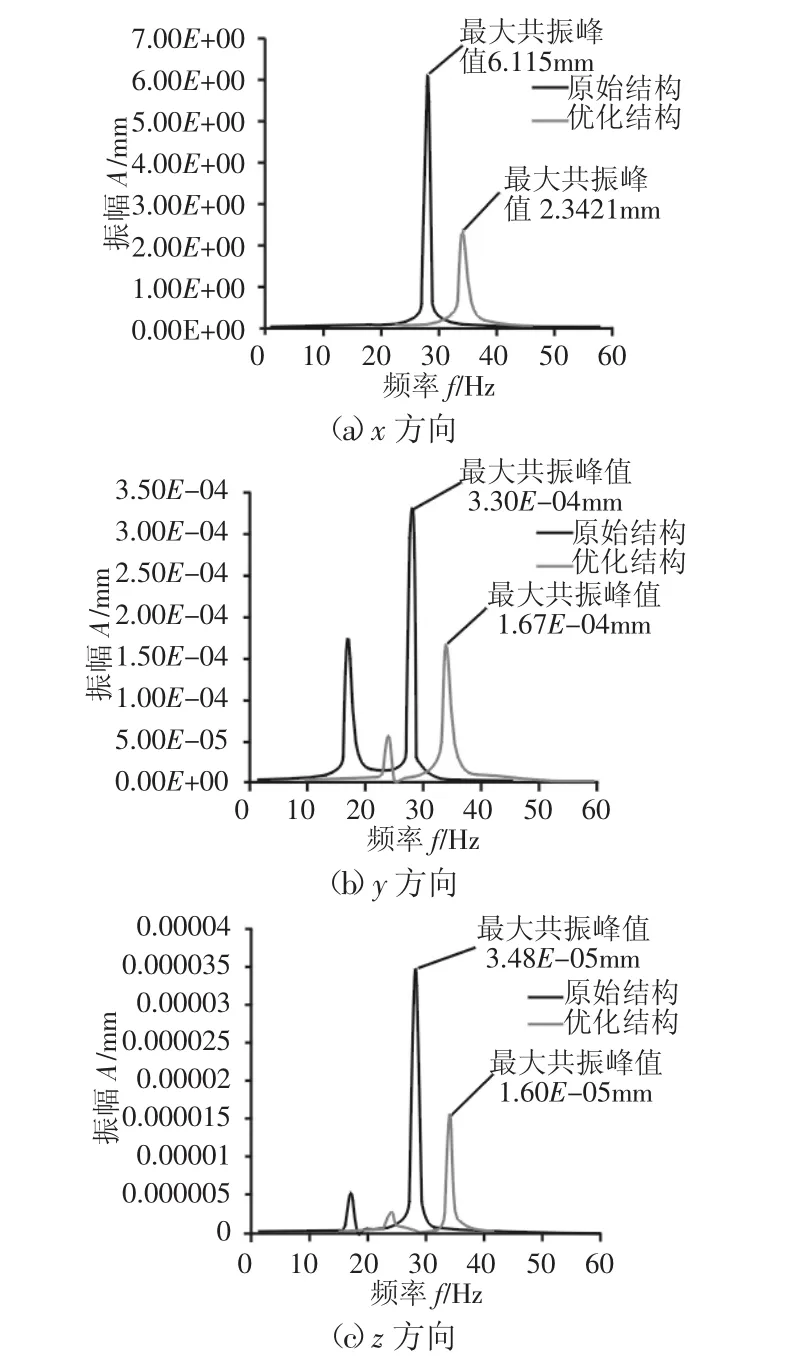
圖6 轉子系統優化前后三個方向諧響應分析對比Fig.6 Comparison of Harmonic Response in Three Directions of Rotors System before and after Optimize

由表4和圖6分析可知，在三個方向上，轉子系統的最大共振頻率均由原始結構的28.097Hz提高到34.976 Hz；并且在x方向對應的最大共振峰值下降了61.7%，在y方向上下降了49.4%，z方向下降了54.0%。以上分析結果表明：轉子系統結構在三個方向上的最大共振峰值均得到了大幅度地降低，這說明其抵抗外界動態干擾的能力得到了較大的提高。

綜上所述，在減輕盤體質量與保證轉子系統靜剛度的前提下，優化后的盤體結構能夠改善轉子系統的動態性能。

5 結論

（1）通過對圓盤造球機懸臂轉子系統的模態分析，得出盤體是對轉子系統低階振型影響程度最大的結構件，由諧響應分析表明轉子系統x、y、z方向上的最大振幅值分別為：6.115mm，3.30×10-4mm，3.48×10-5mm均出現在28Hz即系統的第四階固有頻率，由此可以確定盤體是轉子系統動態性能的薄弱環節。

（2）確定盤體結構是優化目標后，采用靈敏度分析的方法計算盤體分析尺寸對其結構的模態和質量的影響程度，確定優化尺寸參數，避免了對盤體優化的盲目性。

（3）通過ANSYS Workbench優化分析得到5組候選設計點，在此基礎上通過基于熵權的模糊物元法獲取最優設計方案。優化設計結果表明，與原始結構相比，轉子系統在x、y、z三個方向上的最大振幅分別下降約60.5%、49.4%、54.0%。