基于拉普拉斯譜圖理論的隨機游走信號降噪方法研究

趙晨熙

（1.頁巖油氣富集機理與有效開發國家重點實驗室，北京 100101；2.中國石化石油工程技術研究院，北京 100101）

1 引言

在科學研究和實際工業生產過程中，掌握設備的運行和服役狀態是保障設備運行安全的重要手段。設備狀態信號的獲取往往需要經采集、轉換和傳輸等過程，在這個過程中往往會受到傳感器、設備、環境等因素的影響，導致獲取的設備狀態信號中不可避免地包含了大量的噪聲信號，甚至真實信號完全湮沒在噪聲信號中，因此如何對獲得信號進行降噪，就成為真實掌握設備運行和服役狀態的關鍵科學和技術問題之一[1-2]。

近年來，信號降噪的研究獲得了世界范圍內的廣泛關注，國內外的專家學者提出了不同的信號降噪算法，并且在實際工程應用中取得了一定的效果。其中比較典型的方法包括局部投影降噪、小波降噪、相空間重構、形態學方法。文獻[3]研究了相空間重構的降噪算法，將振動信號的吸引子在相空間重構，然后利用奇異值分解法對重構后的吸引子進行計算，并利用奇異譜特性來提高信號的信噪比。文獻[4]研究了加權相空間的降噪方法，將一維時間序列延拓到高維相空間，可以獲得信號在高維相空間的吸引子，從而實現對振動信號降噪。文獻[5]研究了基于相空間重構的局部投影降噪算法，并且進一步提出了鄰域自適應選取的局部投影非線性降噪方法[6]。文獻[7]研究了柔性形態濾波及形態濾波方法，并應用于軸承故障診斷。文獻[8]對小波降噪開展了大量的研究工作，并在機械設備狀態監測和故障診斷領域得到應用。此外，還有很多高校、科研院所的專家學者對信號降噪方法進行了大量研究。

相空間重構法是典型的降噪算法，以局部投影和奇異譜為代表，這些算法不需預知混沌動力學方程，但矩陣運算的計算量大。相空間重構算法包含的二個重要參數是嵌入維數和時間延遲，這兩個參數僅僅只是理論上證明了其存在性，尚未給出具體的表達式，而且在噪聲的干擾下，參數不僅計算困難而且難以選取，導致算法的應用受到極大的限制。小波降噪算法作為應用范圍較廣的傳統降噪方法，對于信號的局部特征具有較強的探測能力，但同樣面臨參數選取難的問題，影響了降噪效果。數學形態學降噪方法需要選取合適的結構元素類型和長度，并且對沖擊信號降噪更為敏感，在實際應用中具有一定的局限性。

因此，提出了一種基于拉普拉斯譜圖理論的隨機游走信號降噪方法，避免了現有算法參數多、閾值選難、要很強的前提假設或者大量的先驗知識等問題。仿真試驗表明，在相同的試驗條件下，提出的降噪算法與小波降噪、自適應降噪和奇異譜降噪算法相比，能夠獲得更好的信噪比，具有更強的降噪效果。

2 拉普拉斯譜圖理論及隨機游走

譜圖理論[9]是微分幾何領域的一個分支理論，在高維數據降維以及聚類等領域得到了廣泛的應用。譜圖理論主要涉及圖的鄰接矩陣譜和圖的Laplacian矩陣譜，通過鄰接矩陣和Laplacian矩陣的表示方法，計算矩陣的特征值和特征向量，依據一定的規則選擇特征向量，實現數據的低維嵌入。

任意特定空間的點集都可以用無向圖G來表示，假設其中V表示頂點集合，E表示邊的集合，則G=（V，E）。假設數據的樣本集為X，在數據點和圖的頂點之間建立一一對應關系，在這里定義成對數據點的相似度為圖中的邊，根據數據點建立與之對應的圖。

隨機游走（Random Walk）是隨機過程的重要組成部分，給定出發點和圖，隨機地選擇鄰居節點，并且移動到鄰居節點上，其特點是隨機游走是一種不規則的變動形式，而且每一步都是隨機的。然后把當前的鄰居結點作為出發點，不斷地重復上述過程，被隨機選出的結點構成了一個在圖上的隨機游走過程[10]。在給出圖上的隨機游走的定義前，需要給出如下的符號和說明。

（1）頂點度對角陣

（2）圖G的容量（Volume）

3 拉普拉斯譜圖上的隨機游走構造方法

3.1 拉普拉斯譜圖上的隨機游走構造方法

由于這里的隨機游走方法建立在圖上，所以，首先定義一個圖 G=（V，E）：

（1）V=｛v1，v2，…，vn｝表示頂點集，其元素 vi表示第 i個頂點，n為頂點數；

（2）E=｛e1，e2，…，en｝表示邊集，元素ek=（vi，vj）為表示連接頂點 vi和 vj的邊，且 E?V×V。

在譜圖理論中包括鄰接矩陣和Laplacian矩陣，選擇鄰接矩陣來描述。

鄰接矩陣：設 G 的頂點集 V（G）=｛v1，v2，…，vp｝，令：

由元素Wij（i，j=1，2，…，p）構成的p階矩陣為圖G的鄰接矩陣（adjacent matrix），記作 W（G）。

圖上頂點的度數表示為D（vi）：

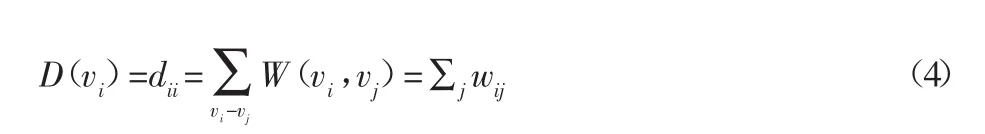
因此，可以定義圖上的隨機游走：將圖上的頂點vi作為隨機粒子，并從該點出發，以正比于這兩點之間邊的權重概率，從這一點轉移到它的領域點vj。定義其轉移概率如下：

即：P=D-1W

在圖G上引入離散的拉普拉斯算子Δ如下：

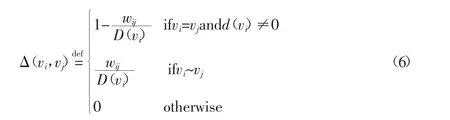
即：Δ=I-D-1W=I-P

此時，我們可以定義圖上的微分方程如下：

式中：λ—λ＞0的常數。

利用隱式歐拉公式（Implicit Euler-Scheme）對微分方程（5）進行求解：

采用k近鄰的方法構建鄰接圖（Weighed k-NN Graph），同時為了保證鄰接矩陣具有更好正定性，采用熱核函數進行計算，構造如下：

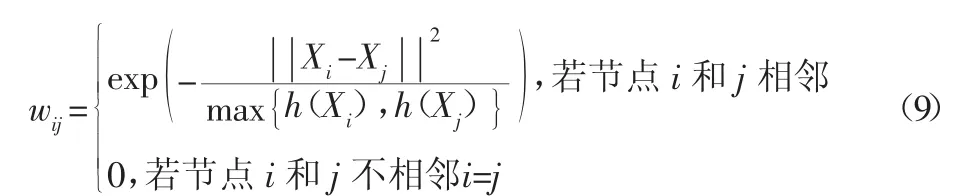
式中：h（Xi）—k-NN 距離。

3.2 算法詳細步驟

基于拉普拉斯譜圖上的隨機游走算法的步驟，如表1所示。

表1 算法步驟Tab.1 Steps of Algorithm

具體的流程圖，如圖1所示。

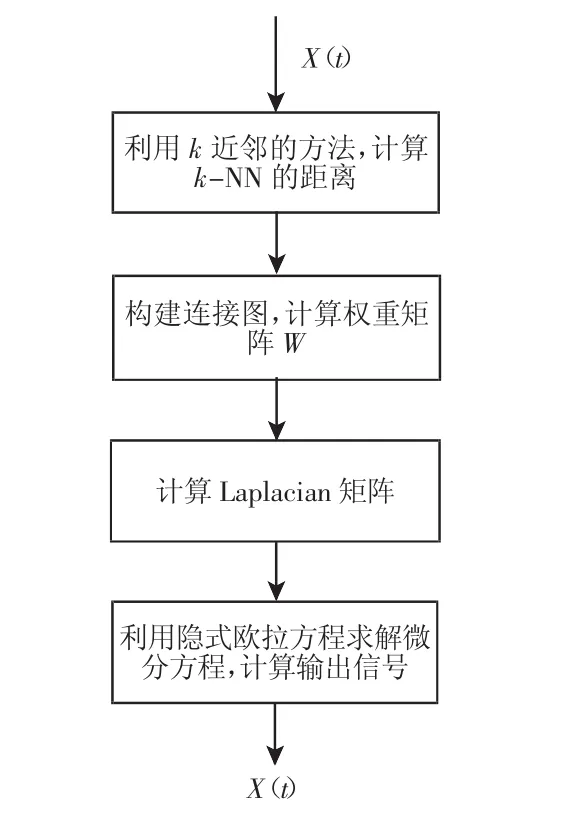
圖1 算法流程圖Fig．1 Flowchart of Algorithm

4 仿真實驗與結果分析

采用sinc函數和方波函數進行方法有效性驗證，sinc函數y=sinx/x+N（0，σ2），x∈［-10，10］，在 x的范圍內分別取 500 個點作為訓練樣本，噪聲方差分別為σ2=0．2和σ2=0．4（高斯白噪聲）；方波為周期T=1．5，幅值為2的函數，噪聲方差為σ2=0．4，對該兩組函數進行實驗，并與小波降噪、自適應濾波降噪（LMS）、奇異譜降噪（SVD）等方法進行對比。

首先對sinc函數進行降噪實驗，如圖2～圖9所示。其中，t—隨機游走步數。利用信噪比衡量數據降噪后的效果，即SNR（Signal to Noise Ratio），單位為：db（分貝）。

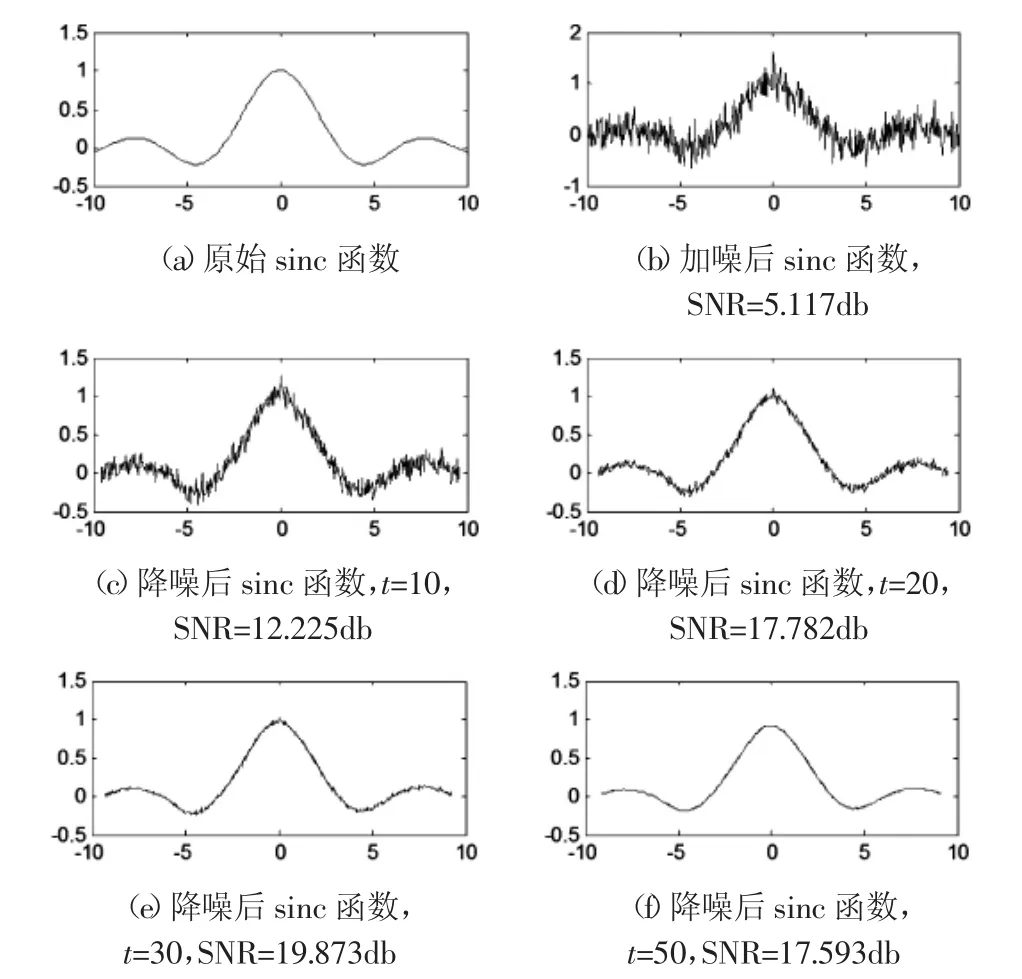
圖2 噪聲δ2=0．2的sinc函數隨機游走降噪結果Fig．2 Denoise Result of Random Walk of Sinc δ2=0．2

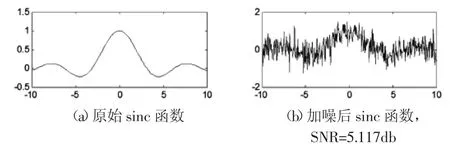
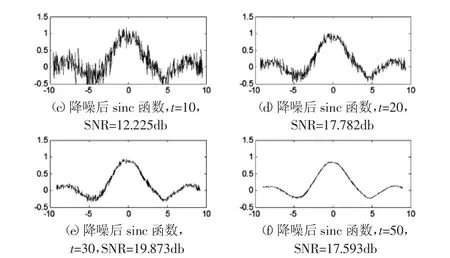
圖3 噪聲δ2=0．4的sinc函數隨機游走降噪結果Fig．3 Denoise Result of Random Walk of Sinc δ2=0．4

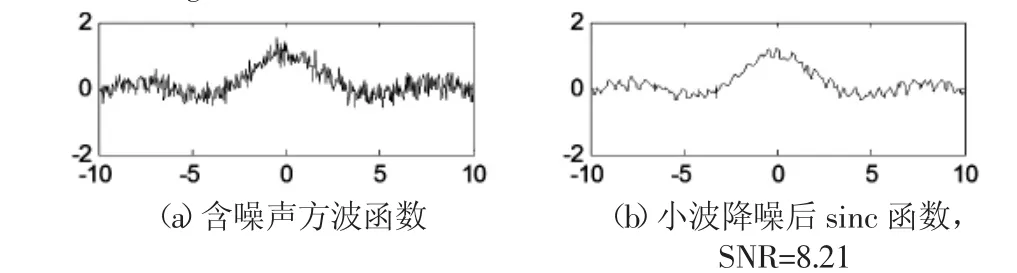
圖4 噪聲δ2=0．2的sinc函數小波降噪結果Fig．4 Denoise result of Wavelet Analysis of Sinc δ2=0．2

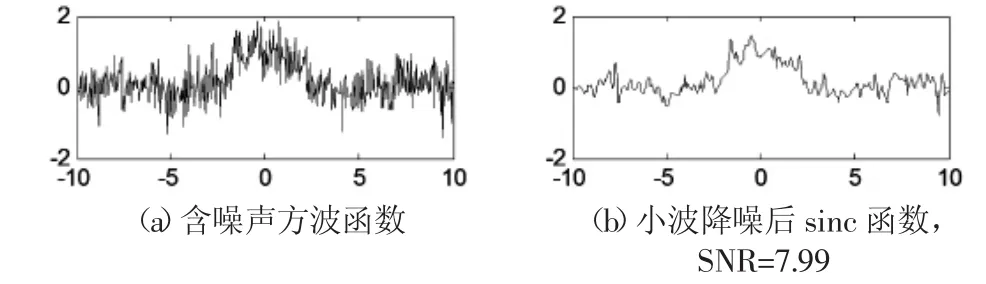
圖5 噪聲δ2=0．4的sinc函數小波降噪結果Fig．5 Denoise result of Wavelet Analysis of Sinc δ2=0．4

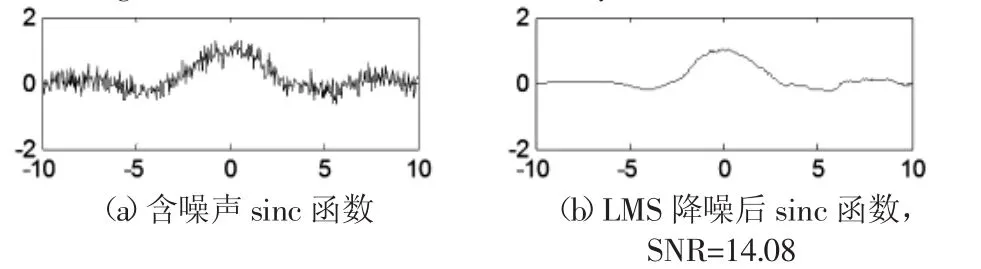
圖6 噪聲δ2=0．2的sinc函數LMS降噪結果Fig．6 Denoise Result of LMS of Sinc δ2=0．2

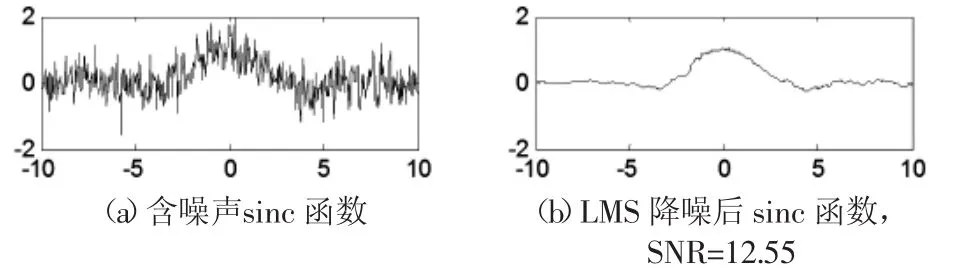
圖7 噪聲δ2=0．4的sinc函數LMS降噪結果Fig．7 Denoise Result of LMS of Sinc δ2=0．4

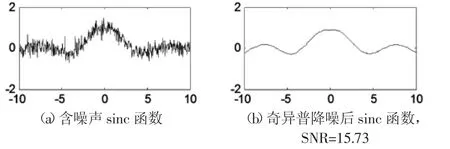
圖8 噪聲δ2=0．2的sinc函數奇異譜降噪結果Fig．8 Denoise Result of Singular Spectrum of Sinc δ2=0．2

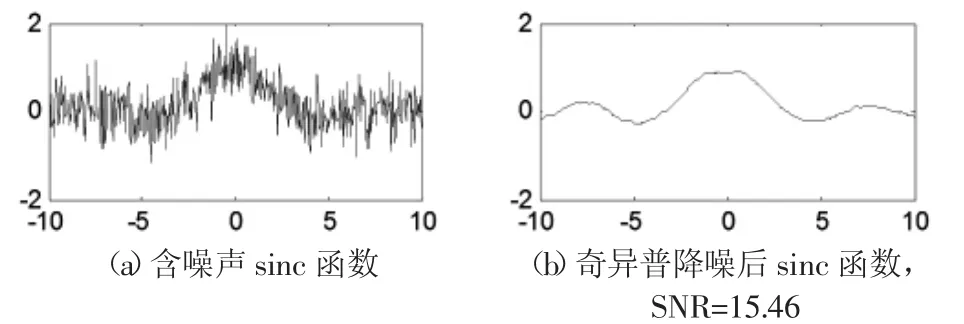
圖9 噪聲δ2=0．4的sinc函數奇異譜降噪結果Fig．9 Denoise Result of Singular Spectrum of Sinc δ2=0．4

對方波函數進行降噪實驗（圖略）。其中，t為隨機游走步數。利用信噪比衡量數據降噪后的效果，即SNR（SignaltoNoiseRatio），單位為：db（分貝）。具體的比較結果，如表2所示。

表2 算法比較結果Tab.2 Compare Result of Algorithm

從實驗結果可知，基于圖上的隨機游走降噪方法普遍優于其他方法，而且隨著游走步數的增加，降噪效果逐漸增大。小波算法在進行信號降噪時，需要專家經驗或窮舉試湊的方法找到合適的分解層數和閾值，特別是閾值的選取對信號的降噪效果影響較大，不同的信號類型，需要采用不同的閾值選取方法；LMS算法是基于最小均方誤差準則和最陡下降法，其步長因子、濾波的階數、特征權矢量初始值等對降噪效果有直接影響，特別是濾波的階數，在信號濾波之前，LMS算法的階數是未知的，若給定的階數小于真實的階數，對LMS的估計會帶來很大的誤差，若高于真實的階數，則會導致訓練時間太長，甚至無法收斂；奇異譜降噪首先將信號進行相空間重構，然后對重構后的信號進行SVD分解，保留分解后對角陣的前k個奇異值，該方法的關鍵是確定對角陣的有效k個奇異值，常用的方法是包括試湊法或閾值法，都依賴于經驗，大大影響降噪效果。基于拉普拉斯譜圖理論的隨機游走方法，把在高維空間中呈現高度復雜的數據集，在低維空間中恢復其內在結構，挖掘數據集的本質規律。將一維的信號數據構建連接圖，根據連接圖計算出拉普拉斯譜圖，在譜圖利用隨機游走方法對原始信號降噪處理，更好的還原出真實的信號，實驗結果充分說明了這里方法的有效性。但是，這里算法也存在一個缺陷，就是隨機游走的步數難以確定，需要通過實驗獲得，通過上面3組實驗可知，降噪效果隨著游走的步數增加而增大，步數達到50時，算法基本趨于穩定。

5 結論

提出一種基于拉普拉斯譜圖理論的隨機游走信號降噪方法，通過將基于拉普拉斯譜圖的流行學習方法和隨機游走方法相結合，能給提取出了信號中的本質信息，較好的去除了干擾噪聲，通過和小波降噪、LMS和SVD算法比較，這里方法具有更高的信噪比，從理論和實驗上均證明了這里方法的有效性和優越性。