考慮物料層作用液壓圓錐破碎機動力學分析

程相文，于 巍

（華北理工大學 機械工程學院，河北 唐山 063009）

1 引言

傳統液壓圓錐破碎機存在耗能高，產量低，產品粒度不理想等缺點，為了讓液壓圓錐破碎機達到更好地破碎效果，對其破碎過程進行動力學分析是十分必要的。

液壓圓錐破碎機工作過程中，破碎物料存在能量積累與耗散，在動錐與定錐之間傳遞能量，因此，破碎物料層是液壓圓錐破碎機破碎系統重要組成部分[1]。物料破碎過程中存在滯回現象，目前國內外研究現狀：

2010年，文獻[2]從物體之間的摩擦滯回特性角度出發，進行遲滯摩擦阻尼器的研究開發，通過物理實驗得出滯后特性，進一步優化分析模型；2011年，文獻[3]研究圓錐破碎機動力學特性，分析破碎運動過程中物料的滯回特性，采用分段雙線性遲滯模型，構建動力學微分方程，實現破碎機的動力學特性分析；2014年，文獻[4]考慮物料對稱滯回性質對壓路機振動輪進行響應特性分析，應用雙線性對稱滯回模型表達物料的滯回特性，從而建立系統動力學模型，實現系統動力學分析；2015年，文獻[5]對Bouc-Wen滯回模型特性和能量耗散進行研究分析，實現對封閉的循環位移滯回模型能量耗散的數值評價，可應用到機械系統的振動響應中，表達破碎物料非線性滯回力；2015年，文獻[6]基于物料顆粒的相互作用，對機械模型進行數值分析和研究，得到簡化的顆粒接觸特性，并運用離散元法實現仿真分析。

通過擠壓破碎動力學仿真實驗[7]，不難發現物料層滯回作用與曲線模型下非線性力更為接近，雙線型等分段直線型模型僅能初步對滯回現象進行近似，與實際差異較大。研究液壓圓錐破碎機破碎系統運動情況，建立三維動力學模型，采用具有光滑特性的曲線滯回模型Bouc-Wen模型，利用合理的等效線性化方法進行求解，實現對液壓圓錐破碎機的動力學分析。

2 液壓圓錐破碎機動力學模型

2.1 液壓圓錐破碎機主要結構和工作原理

液壓圓錐破碎機主要結構，如圖1所示。液壓圓錐破碎機工作原理：電動機提供動力，經由錐齒輪帶動偏心套及主軸進行旋擺運動，由于存在偏心，使動錐和定錐之間距離發生周期性增大和減小，從而實現物料的擠壓和破碎，同時，液壓裝置可帶動動錐做上下運動，控制排料粒度和過鐵保護。

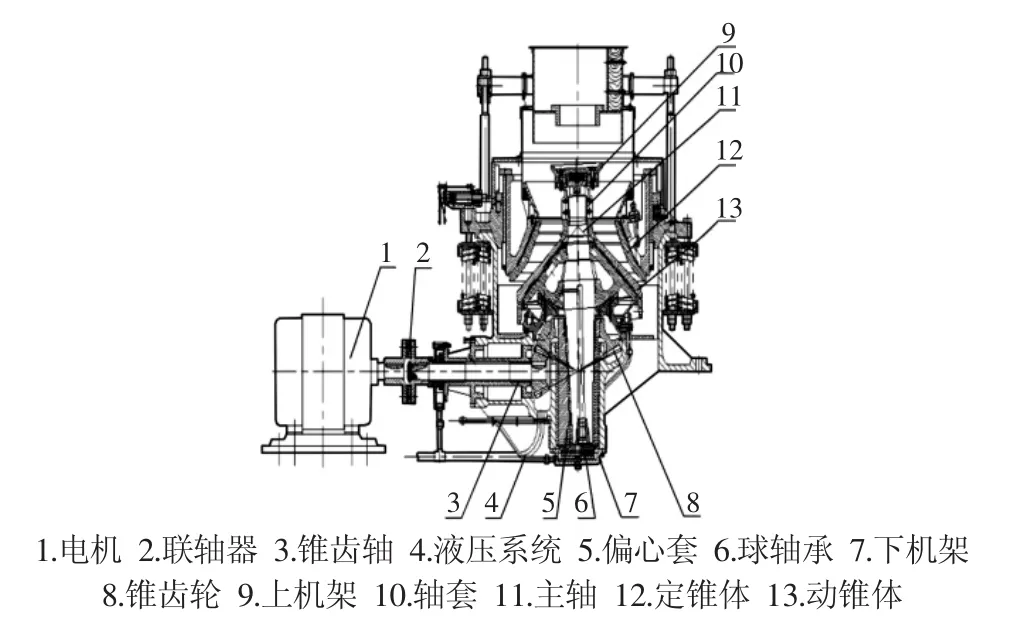
圖1 液壓圓錐破碎機結構示意圖Fig.1 The Structure Diagram of Hydraulic Cone Crusher

2.2 液壓圓錐破碎機動力學模型建立

液壓圓錐破碎機破碎系統動力學模型，如圖2所示。動錐剛體做空間運動，具有3個自由度，分別為沿動錐軸向移動Z，徑向移動r，繞動錐軸心的轉動θ，偏心塊作為質點連接在動錐上，動錐靜止時質心位置O，建立絕對坐標系（r，θ，z），動錐運動時質心位置 O′，建立相對坐標系（r′，θ′，z′），動錐的進動角，破碎過程中受物料滯回力作用。

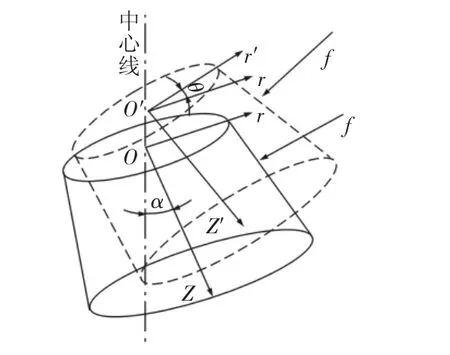
圖2 液壓圓錐破碎機動力學模型Fig.2 Dynamics Model of Hydraulic Cone Crusher

動錐在電動機扭矩的作用下圍繞中心線轉動，物料產生擠壓破碎，與動錐之間存在摩擦，使動錐發生周向自轉；偏心塊作用簡諧激勵，實現動錐的偏擺運動，同時物料對動錐產生非線性滯回力；液壓系統控制動錐沿其軸向方向的運動，考慮動錐的進動角α很小，其垂直分力近似為重力，因此，建立液壓圓錐破碎機的動力學微分方程：

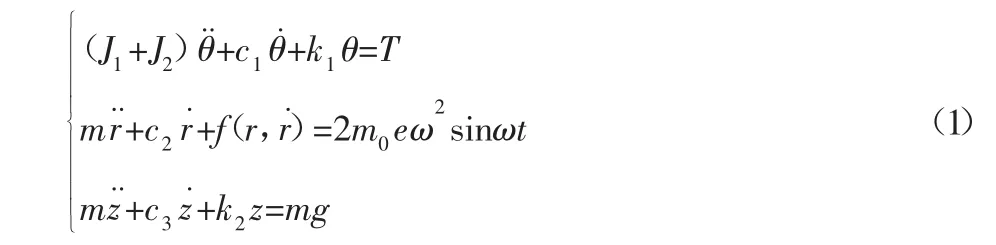
式中：J1—動錐繞中心線轉動慣量，kg/m2；J2—動錐自轉轉動慣量，kg/m2；m—動錐參振質量，kg；m0—偏心塊質量，kg；T—電動機扭矩，N/m；c1—動錐周向阻尼系數；c2—動錐徑向阻尼系數；c3—動錐軸向阻尼系數；k1—動錐周向剛度系數，N/m；k2—液壓系統等效剛度系數，N/m；ω—偏心塊回轉角速度，rad/s；θ—動錐轉過角度，rad；r—動錐徑向位移，m；z—動錐軸向位移，m；e—偏心塊的偏心距離，m；f（r，r˙）—物料的非線性滯回力，N；

3 物料非線性滯回力研究

3.1 非線性滯回力模型的建立

液壓圓錐破碎機破碎過程中，物料層非線性滯回力對破碎運動影響很大，因此，合理分析物料層非線性滯回力，從而提高液壓圓錐破碎機動力學分析的準確性。

液壓圓錐破碎機破碎腔中散體物料會形成具有一定松散程度的物料層。破碎初始階段，物料對動錐的應力逐漸增大，同時，應力-應變斜率快速加大，當物料破碎到一定粒度時開始下落，此時應力仍然繼續增大，但應力-應變斜率逐漸減小；動態應力-應變曲線達到峰值后進入卸載階段，料層貯存能量進行釋放，用于料層顆粒的破碎，由于物料層具備強化性質，將卸載剛度看作與加載時相等。因此，以Bouc-Wen模型[5]描述破碎物料層非線性滯回力，如圖3所示。

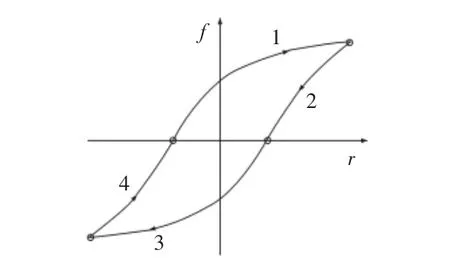
圖3 物料層非線性滯回力模型Fig.3 The Nonlinear Hysteretic Force Model of Material Layer

Bouc-Wen模型表達式[5]：

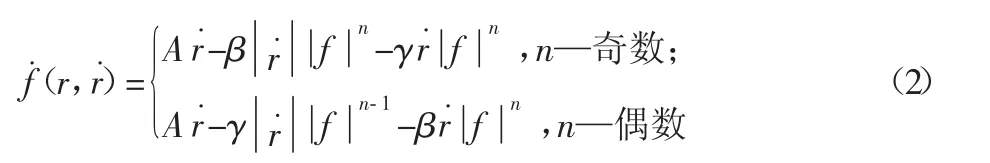
式中：A—系統振幅控制參數；β、r—滯回環尺寸與形狀控制參數；n—滯回環彈性區域到非彈性區域過渡光滑性控制參數。

3.2 非線性滯回力的等效線性化

對于式（1）b這樣的非線性系統，求解其非線性微分方程較困難。在分析諧波激勵振動系統時，常采用諧波平衡法或函數描述法[8-9]對非線性系統的非線性項進行等效線性化處理，其中非線性項與系統激勵同頻率，且為系統變量顯函數，但式（2）是關于r與r˙的隱函數，因此，在函數描述法基礎上加以改進，對式（2）進行等效線性化處理，進一步實現非線性微分方程式（1）的求解。

由式（1），假設非線性函數 f輸入項 r（t）=Rsin（τ），其中 τ=ωt+φ，根據函數描述法[9]f等效線性化表達式：

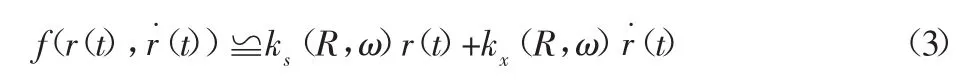
式中：ks、kx—等效剛度系數和等效阻尼系數，將式（3）進行復數變化[10]，得：

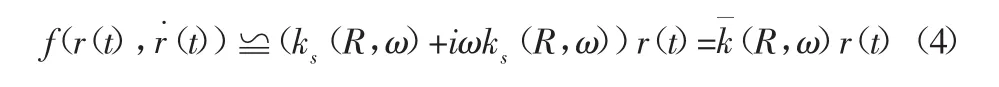
式中：kˉ—等效線性化系數，根據函數描述法[9]可知：

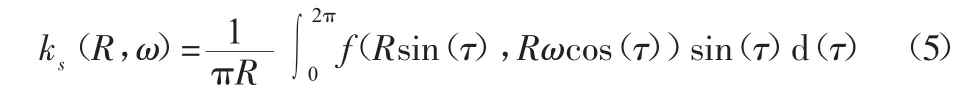
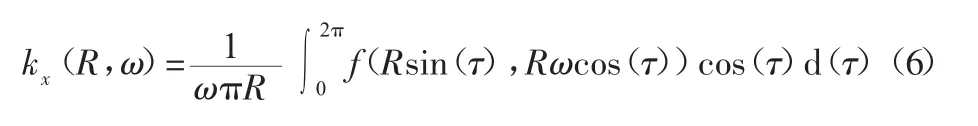
顯然，結合式（2）、式（5）和式（6）是無法直接求出 ks、kx，這體現了函數描述法的弊端，即無法對表達式為隱函數的非線性項進行等效線性化，因此為解決以上問題，分別對式（5）、式（6）兩式進行時間t的一階求導，得：

由圖3可知，根據f與r˙數值的正負，可將圖3的滯回環分成四個部分，因此f表達式簡化為如下形式：

其中，η1、η2的取值，如表 1 所示。

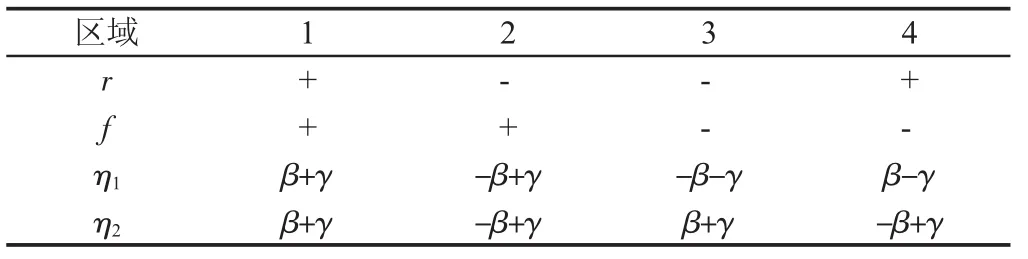
表1 滯回環不同區域對應的系數η1、η2Tab.1 The Coefficients η1and η2for Different Intervals of Hysteresis Loop

將式（12）代入式（11），得：

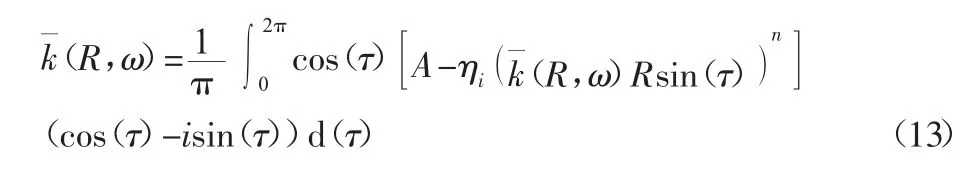
式中：當n—奇數時i=1；當n—偶數時i=2。

根據圖 3 可知，滯回環各相鄰部分的r˙（t）異號，所以式（13）中對應的積分區間為：

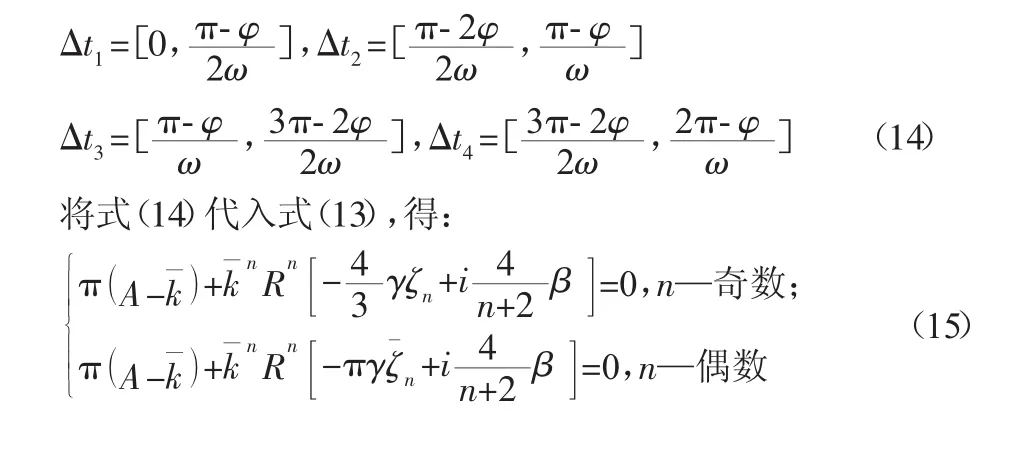
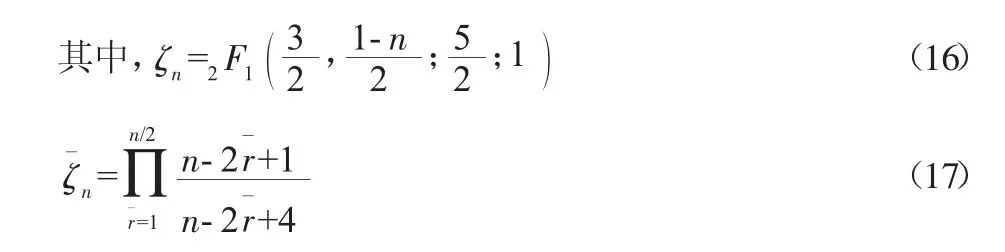
由式（16）、式（17）不難發現，n 取不同值時，ζn、ζˉn取值不同，當 n=1 時，ζn=1，ζˉn=1。把對應 n 值的 ζn及ζˉn代入式（15），便可得到相應階數下的kˉ值。

4 液壓圓錐破碎機動力學分析

將非線性項f（r，r˙）等效線性表達式（3）代入式（1）b，得：

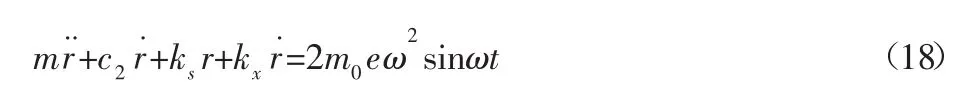
求解式（18），得等效線性化振動系統（18）響應振幅R為：

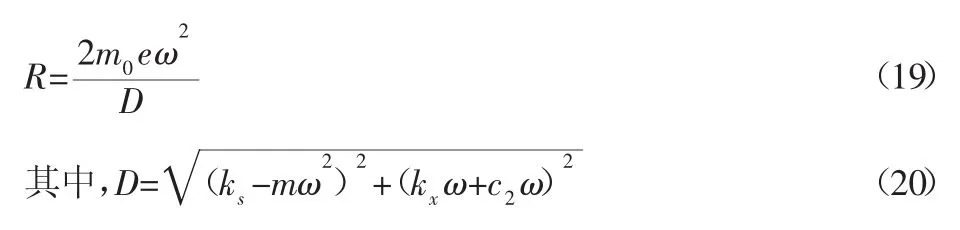
聯立式（15）～式（17），可得不同階數 n 對應 ks、kx表達式，并將其分別代入式（19）、式（20），得出對應階數響應振幅R。文獻[11]對Bouc-Wen模型參數靈敏性進行分析，可知n具有很低的靈敏性，隨著n值增大，滯回環光滑度逐漸降低，因此，為了使滯回環具有足夠光滑度，取 n=1，則（3）式 ks、kx為：

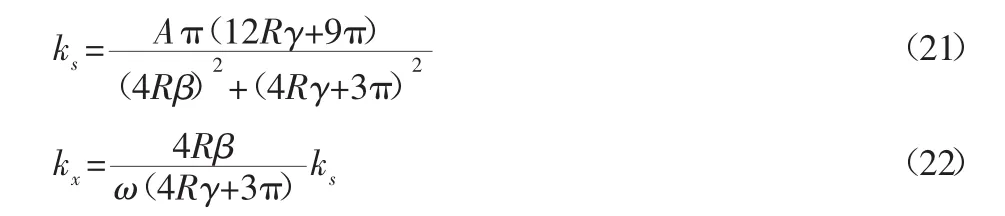
對液壓圓錐破碎機破碎系統進行動力學分析，選定表2中參數值。

表2 系統結構參數和幾何參數Tab.2 Parameters of Structure and Size in System

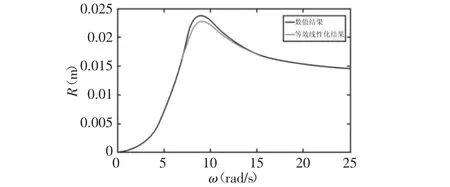
圖4 考慮物料作用時動錐徑向運動幅頻響應曲線Fig．4 The Amplitude-Frequency Response Curve of Moving Cone with Considering The Effect of Materials

將表2參數值代入式（1），通過Matlab軟件，求解得破碎機動錐在徑向方向上振幅R隨外部激勵角速度ω變化曲線圖，如圖4所示。數值結果與等效線性化結果對比，不難發現通過等效線性化方法可以較準確反映破碎機動錐動力學特性。不考慮破碎腔內物料作用時，破碎機動錐振幅變化曲線，如圖5所示。曲線隨角速度ω增大而逐漸上升，最終趨于平穩，該曲線不存在由于物料作用產生共振波峰，如圖4所示。

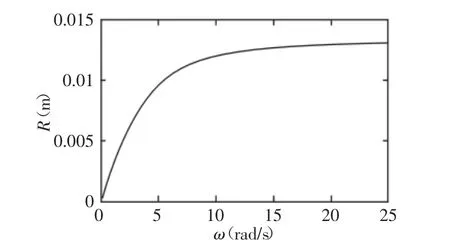
圖5 不考慮物料作用時動錐徑向運動的幅頻響應曲線Fig.5 The Amplitude-Frequency Response Curve of Moving Cone without Considering The Effect of Materials

研究特定參數A、m0、m、e取不同數值時，對液壓圓錐破碎機動錐振幅影響。隨著參數A增大，動錐共振振幅隨之增大，且其共振頻率逐漸增大，隨著ω的增大，動錐振幅最終趨近一數值；隨著偏心塊質量小幅增加，動錐振幅出現較為明顯的增大現象，且振幅最終趨近的數值有所增大。隨著動錐質量的逐漸增大，動錐共振振幅減小，共振頻率有較為顯著的減小趨勢，動錐振幅的趨近值有所減小。隨著偏心距的小幅增大，動錐振幅出現了明顯的增大現象，且振幅最終趨近值有所增大（圖略）。

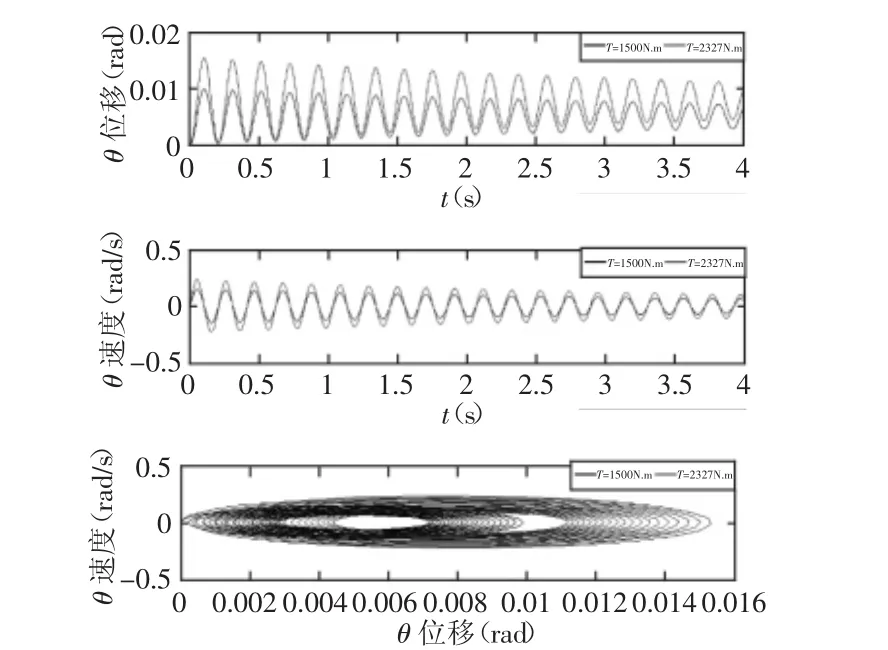
圖6 動錐周向運動時間響應曲線及相平面曲線Fig.6 The Time Response Curve and Phase Plane Curve of Moving Cone Circumferential Movement

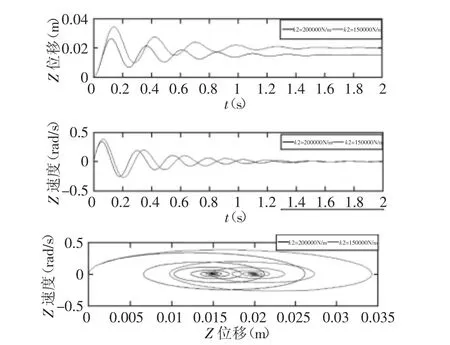
圖7 動錐軸向運動時間響應曲線及相平面曲線Fig.7 The Time Response Curve and Phase Plane Curve of Moving Cone Axial Movement

對液壓圓錐破碎機動錐進行周向時間歷程運動分析，得出時間響應曲線及相平面曲線，如圖6所示。θ位移和速度的振幅具有有界性，并隨時間衰減，增大電動機扭矩T，θ位移及速度的振幅明顯減小；對液壓圓錐破碎機動錐進行軸向時間歷程運動分析，得出時間響應曲線及相平面曲線，如圖7所示。z位移及速度的振幅同樣具有有界性，并隨時間衰減，增大液壓系統等效剛度系數k2，z位移及速度的振幅明顯減小。

5 結論

（1）研究液壓圓錐破碎機破碎運動過程，將Bouc-Wen模型作為物料層滯回力模型，使物料層對動錐的作用更加符合實際情況，通過合理地等效線性化方法，解決Bouc-Wen模型非線性項難以求解的問題，進一步實現對破碎系統的動力學分析。

（2）通過圖4與圖5對比不難發現隨著激勵角速度的增大，圖4考慮物料層作用的動錐振幅存在明顯的波峰且遠遠大于圖5未考慮物料層作用的情況，由此可知物料層具有很好的儲能與放能作用，物料層的這一性質可以為液壓圓錐破碎機節能優化研究提供極大幫助。

（3）通過圖可知，動錐振幅對破碎機的一些參數具有不同程度的敏感性，其中對偏心塊質量及偏心距較為敏感，對動錐質量，Bou-Wen模型參數A的敏感性較差，同時由于參數的變化，破碎系統的共振頻率存在不同程度的偏移。

（4）非線性滯回系統作為動力學研究的一項前沿課題，具有十分豐富及復雜的動力學特性，滯回系統引入Bouc-Wen模型，可以更為合理的反映液壓圓錐破碎機破碎系統的動力學行為。