容積調速系統特性分析與擾動控制研究

王黎光，徐海波，王威威，李 奔

（1.中國工程物理研究院總體工程研究所，四川 綿陽 621900；2.西安交通大學 機械工程學院，陜西 西安 710049）

1 引言

在軍事發達的國家，行車取力發電已經進入實用階段[1-3]。但國內行車取力發電仍然處于起步階段，其瓶頸問題是發動機轉速大范圍變化的情況下系統輸出轉速穩定的控制問題。文獻[4-6]對泵空馬達容積調速系統進行了PID控制，模糊控制算法等的仿真研究，這些算法的一定程度上適應了液壓系統時變、非線性的特點。

但是由于液壓傳動系統是一個大慣量的系統，具有一定的遲滯特性。以上反饋控制的方法都不能解決控制滯后，調節速度慢的問題。尤其是在應對輸入轉速頻繁大范圍波動情況時沒有取得滿意的結果。

前饋控制算法的理論比較簡單，在穩態控制中對擾動的抑制有重要意義。文獻[7]對前饋控制器最優性能方面進行了研究；文獻[8]對前饋控制器在水電站控制的應用進行了研究；文獻[9]提出采用前饋控制結合反饋控制的方法實現精軋終軋溫度的精確控制；文獻[10]對前饋補償在電液振動臺控制方面的應用進行研究。但目前對于高階的傳遞函數系統來說，前饋方法的整定目前還沒有定論，因此利用前饋控制算法對容積調速系統進行恒速控制方面的理論分析、仿真分析與實驗研究都比較少。

2 行車取力發電容積調速系統原理

行車取力發電容積調速系統原理，如圖1所示。其中，采用電液比例控制的變量泵作為供能元件，定量液壓馬達作為執行元件。變量調節機構集成在變量泵內部，主要由電液比例減壓閥、三位四通閥控液壓缸及變量斜盤等部分組成。變量調節機構是閉環控制回路，屬于力反饋閉環。當控制電流小于起調電流，斜盤處于零點位置，變量泵無排量輸出。當控制電流大于起調電流時，變量斜盤隨之偏轉，變量泵排量輸出與輸入電流大小成線性比例關系。

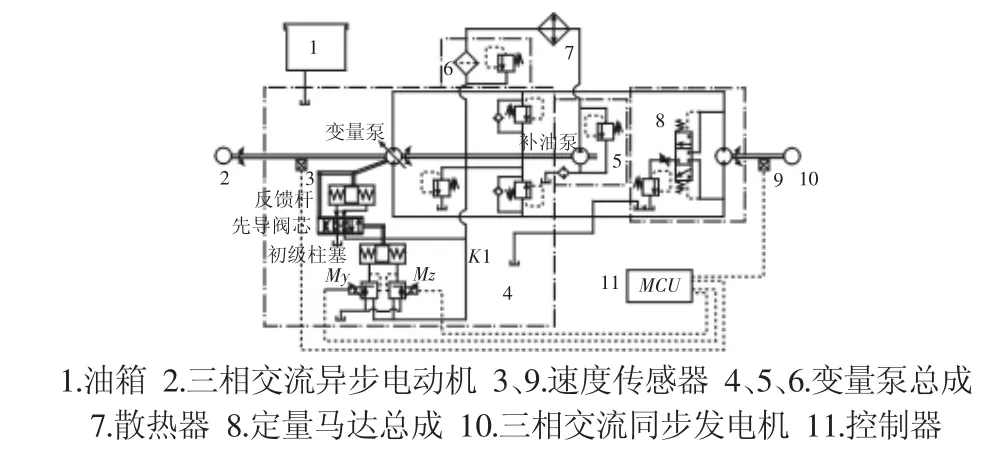
圖1 行車取力發電容積調速系統原理示意圖Fig.1 of Volume Speed-Modulating System

以My電磁鐵通電為例，當My通電電流的增加使得先導壓力作用在初級柱塞左端的壓力大于柱塞所受彈簧力時，初級柱塞右移，先導閥芯隨之右移，使次級柱塞的左端接通控制油壓K1，右端接通殼體，斜盤隨之偏轉，若My輸入電流保持不變，先導閥芯將很快恢復中位，斜盤傾斜角度將不再變化直至My輸入電流再次變化。

可見，該變量泵采用比例電磁鐵減壓閥控制先導變量活塞，伺服閥控制變量斜盤轉動角度，變量活塞和變量斜盤的驅動是由補油泵壓力來推動，該控制方式的控制電流較小，最大排量所對應的控制電流為410mA，液壓泵從最小流量到最大流量響應速度最快可達0.5s，理論上可以滿足控制要求。

3 系統建模與轉速擾動控制仿真分析

3.1 行車取力發電容積調速系統建模

對行車取力發電容積調速系統進行了基于傳遞函數的數學模型的建立，不同于常規建模方法，這里并沒有對變量調節機構—比例電磁鐵、閥控液壓缸等進行詳細完備的建模。而是將變量泵作為一個整體，以電壓作為輸入，梯度排量作為輸出。綜合考慮變量泵的輸入輸出特性，以一階慣性環節來表示變量泵的輸入輸出特性。簡化的模型避免了變量調節機構中各種參數的確定，而這些參數往往是很難準確得到的。簡化后的模型得到了和實際情況吻合較好的結果。

變量泵的變量調節機構屬于力反饋閉環控制回路，變量泵的排量輸出與輸入電流成線性比例關系。根據變量泵輸入輸出關系，電液比例變量泵可以用一階慣性環節來表示：

式中：Dp—變量泵的梯度排量；u—輸入電壓；kp—流量增益；td—時間常數，表征了變量泵的響應時間。查閱變量泵資料，得到 kp=1.2×10-6，td取為 0.035。

泵-馬達系統模型的建立主要是基于液壓理論知識給出泵流量方程、系統高壓腔的流量連續性方程及馬達和負載轉矩之間的平衡方程。通過三個方程的聯立求解得到泵-馬達模型傳遞函數。

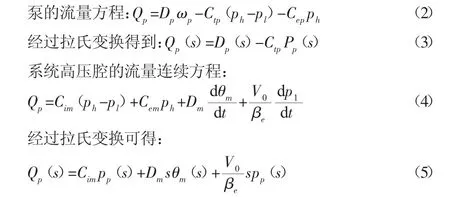
馬達和負載轉矩之間的平衡方程：

根據泵-馬達相關參數計算可以得到傳遞函數中參數。

傳動系統反饋控制用速度傳感器，其動態響應可以看成是一階比例環節，傳遞函數為：

查閱速度傳感器資料得：kf=0.019V·s/rad。

由式（1）、式（10）、式（11）行車取力發電容積調速系統傳遞函數框圖，如圖2所示。

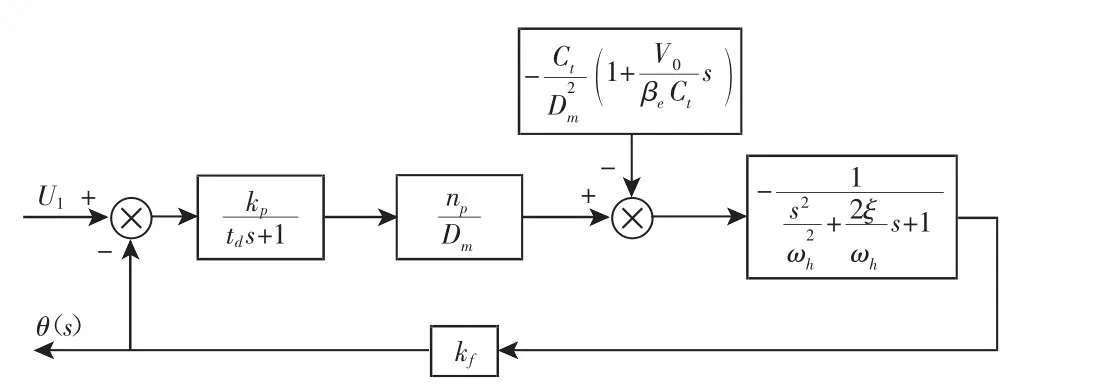
圖2 行車取力發電容積調速系統傳遞函數框圖Fig.2 Transfer Function Block Diagram of Volume Speed-Modulating System

3.2 輸入轉速擾動控制仿真分析

根據傳遞函數框圖在Matlab/Simulink里建立系統的仿真模型，如圖3所示。

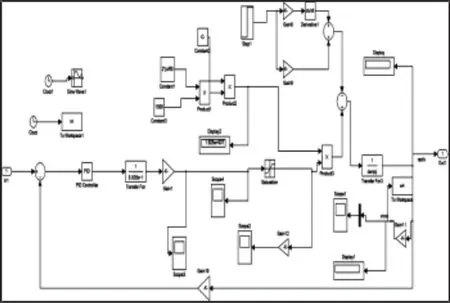
圖3 泵-馬達容積調速系統Simulink模型Fig.3 Simulink Model of Volume Speed-Modulating System

前饋控制是針對擾動的一種控制策略，當擾動一旦產生控制器立刻產生控制量對擾動進行校正，這樣不需要擾動量經過系統產生偏差就提前進行調節。在實際使用中，前饋控制經常和反饋調節一同使用，以降低穩態誤差，提高對擾動的抑制作用。

靜態前饋系數可通過計算法和工程整定法得到。計算法是根據能量守恒或者質量（流量）守恒原理，根據公式計算得到補償量公式，得到靜態前饋系數，具體計算可參考相關文獻。工程整定法是在實際控制實踐中采用試湊法，根據多次運行的試驗結果，得到滿意的靜態前饋系數。實際應用中一般采用工程整定的方法得到，計算得到的靜態前饋系數可以作為工程整定前饋系數的一個參考值。

輸入轉速擾動對系統輸出的影響與轉速擾動量的大小有密切的關系，擾動量越大，系統的瞬態誤差越大。在利用前饋補償速度擾動時，應該考慮不同擾動量對前饋系數的影響。這里就最佳前饋系數和擾動量的大小的關系做了相關的研究。

針對輸入轉速突變，常規PID控制與前饋+PID控制的調節效果比較，如圖4（a）所示。針對不同擾動量下，不同前饋控制系數下，PID+前饋控制效果比較，如圖4（b）所示。

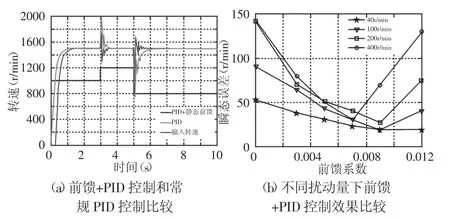
圖4 調節效果比較Fig.4 Regulation Effect Comparison

從圖4（a）可以看出，對于轉速突變而言，靜態前饋減小了速度突增或突減的幅值，對輸入轉速擾動有更快的響應速度。前饋+PID控制相對常規PID控制對輸入轉速擾動有更好的抑制效果。

從圖4（b）可以看出，在轉速變化率相同的情況下，最佳前饋系數基本是一致的，在前饋控制作用下，雖然轉速變化量成比例增加，但是系統輸出瞬態誤差相差卻不大，從29r/min到40r/min。這也為實驗中利用工程法尋找最佳靜態前饋系數提供了依據。

4 實驗研究

本實驗依托于泵控馬達容積調速實驗平臺，如圖5所示。實驗臺由30kW同步發電機，液壓馬達，變量泵，交流電機，散熱器，油箱以及速度傳感器，控制系統等組成。

圖5 泵空馬達容積調速實驗平臺Fig.5 Experimental Platform of Volume Speed-Modulating System

PID控制對輸入轉速擾動的控制效果，如圖6所示。其中設定輸出轉速為750r/min。

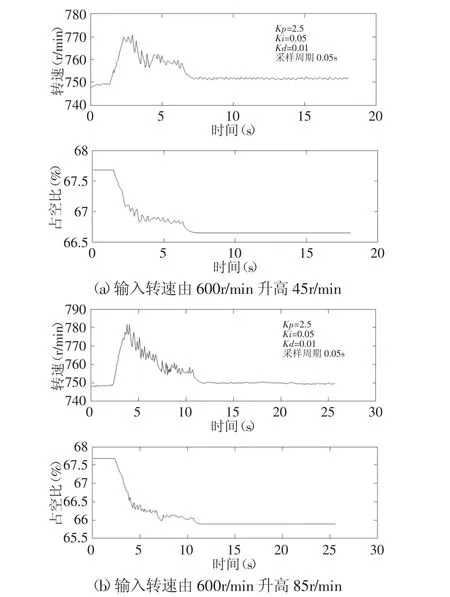
圖6 PID控制對輸入轉速擾動的抑制Fig.6 Control Effects of Rejecting the Disturbance Base on PID Control Algorithm

可見，實驗與仿真結果趨勢大致相同，驗證了理論分析、建模以及仿真分析的合理性，針對輸入轉速擾動的問題，PID控制在5s的時間內能將轉速調節穩定，超調量和轉速變化量有關，轉速變化量越大，超調量越大。

PID+靜態前饋控制對輸入轉速擾動的抑制效果，如圖7所示。設定輸出轉速為750r/min，輸入轉速由600r/min升高85r/min，與6（b）作對比實驗。

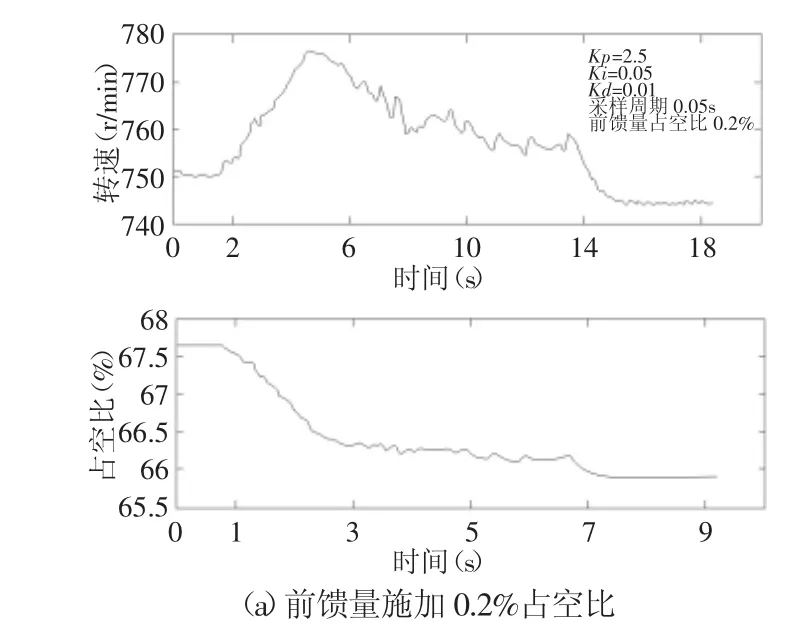
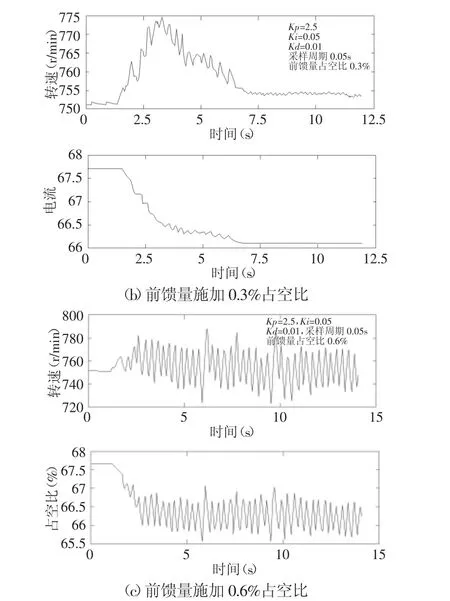
圖7 前饋+PID控制對輸入轉速擾動的抑制Fig.7 Control Effects of Rejecting the Disturbance Base on PID Combined With Feed-Forward Compensation Algorithm

可以看出，與前面仿真得到的結果趨勢大致相同，這進一步驗證了理論分析、建模以及仿真分析的合理性，當前饋量較小時，比單純PID控制優勢不明顯，如圖7（a）所示；前饋量過大時又造成系統震蕩，如圖7（c）所示；當前饋量選擇合適時與常規PID控制相比，即圖7（b）和圖6（b）相比，超調量下降了13%，調整時間縮短了1.5s。可見前饋控制如果參數整定合適時，可以降低系統超調量，縮短調整時間，針對輸入轉速擾動的問題可以明顯改善控制效果。

5 結論

（1）針對行車取力發電容積調速系統輸入轉速擾動引起的馬達轉速波動的問題，提出了PID+前饋控制算法進行補償控制的方法。（2）通過對系統各部分進行分析，建立了泵-馬達容積調速系統Simulink仿真模型，分析了系統輸入轉速變化時系統的響應特性，對前饋+PID控制算法進行仿真研究，對比分析了前饋+PID控制與常規PID控制的控制效果，并對靜態前饋系數的整定規律進行了研究。（3）通過實驗驗證了理論分析、建模以及仿真分析的合理性，通過實驗定量研究了前饋+PID控制相比常規PID控制在應對泵控馬達容積調速系統輸入轉速擾動問題上的控制效果。研究結果表明，相同條件下，在應對輸入轉速擾動時，選擇合適的靜態前饋系數時，前饋+PID控制相比常規PID控制，穩態誤差均為±5r/min，而系統超調量下降了13%，調整時間縮短了1.5s，可見采用前饋+PID控制的控制效果得到了明顯改善。