碼垛機器人修正正弦函數插值的軌跡規(guī)劃

喬 木，于天彪，李 明，王 博

（東北大學 機械工程與自動化學院，遼寧 沈陽 110819）

1 引言

廣泛應用于醫(yī)藥包裝生產線的碼垛機器人是提升整個醫(yī)療行業(yè)自動化水平的關鍵裝備，能夠完美地實現重載、快速、準確和連續(xù)的作業(yè)要求[1]。隨著醫(yī)療行業(yè)的高速發(fā)展和生產規(guī)模的擴大，對碼垛機器人的工作速度提出了更高的要求[2]。因為碼垛機器人在堆垛過程中需要頻繁的啟停和變速，這對碼垛機器人本體和電機會造成較大振動和磨損，所以為了保證碼垛機器人能夠快速平穩(wěn)的作業(yè)，軌跡規(guī)劃過程就顯得尤為重要。

軌跡規(guī)劃是根據具體的任務要求設計機器人的各個關節(jié)位移、速度、加速度以及急動度隨時間t的變化曲線[3]，是碼垛機器人控制的前提和基礎，其運動性能對碼垛機器人的工效、能耗和使用壽命[4]具有重要意義，因此對軌跡規(guī)劃的研究一直是碼垛機器人領域的熱點之一[5]。文獻[6]考慮動態(tài)約束求解時間最優(yōu)軌跡，但加速度曲線不連續(xù)，伴有柔性沖擊。文獻[7-8]采用三次樣條曲線規(guī)劃時間最優(yōu)軌跡，只能確保速度、加速度連續(xù)，無法保證急動度的連續(xù)。國內學者田西勇在組合函數曲線方面亦做出突出貢獻。

在實際生產中，主要采用多項式函數和正余弦函數進行規(guī)劃，但是隨著工作要求的不斷提高，單一曲線已經無法滿足要求[9]。通過三段修正正弦函數曲線在關節(jié)空間對碼垛機器人進行軌跡規(guī)劃，并利用遺傳算法對修正參數進行優(yōu)化，結果表明該方法能夠有效提高碼垛機器人的運動平穩(wěn)性。

2 軌跡規(guī)劃優(yōu)良曲線特性分析與選取

醫(yī)藥碼垛機器人的特點是空間四自由度串聯(lián)關節(jié)型機器人，具有雙平行四邊形結構，完成對藥箱從輸送帶到貨架的簡單搬運，而藥箱姿態(tài)不發(fā)生變化。碼垛機器人的三維實體模型，如圖1所示。

圖1 碼垛機器人實體模型Fig.1 The Entity Model of Palletizing Robot

本研究是建立在位移函數、速度函數和加速度函數連續(xù)的基礎上，以加速度函數為切入點，選取運動性能最優(yōu)的加速度函數曲線。碼垛機器人的關節(jié)變量在工作時間t=0時為θI，t=T時為θF，為了保證碼垛機器人運動的平滑性，應該滿足如下表所示初始條件：

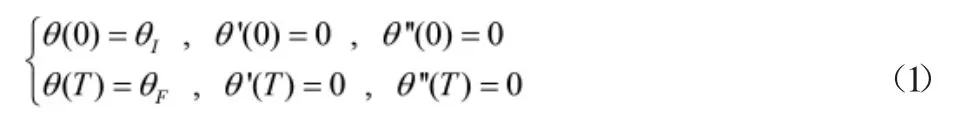
設碼垛機器人關節(jié)軌跡的插值函數為s（τ），則有0≤s（τ）≤1，0≤τ≤1，τ=

根據式可以得到加速度函數為正弦函數的位移、速度、加速度和急動度的方程為：

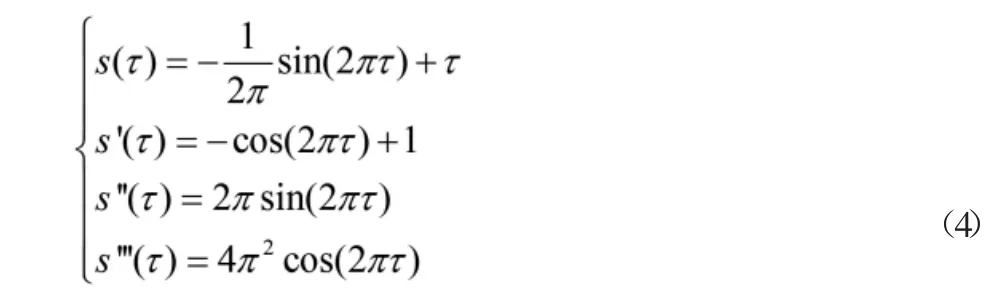
根據式得到加速度函數為余弦函數的位移、速度、加速度和急動度的方程為：

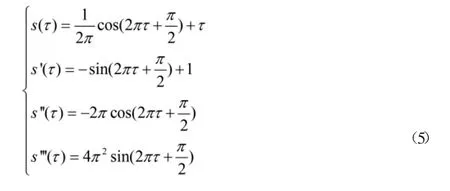
根據式得到加速度函數為線性函數的位移、速度、加速度和

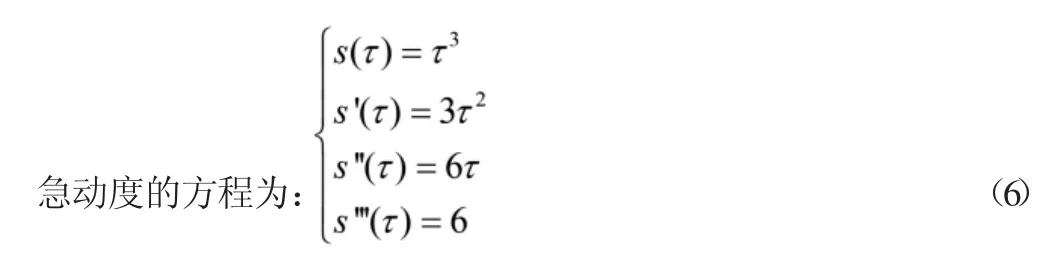
根據式得到加速度函數為三次多項式的位移、速度、加速度

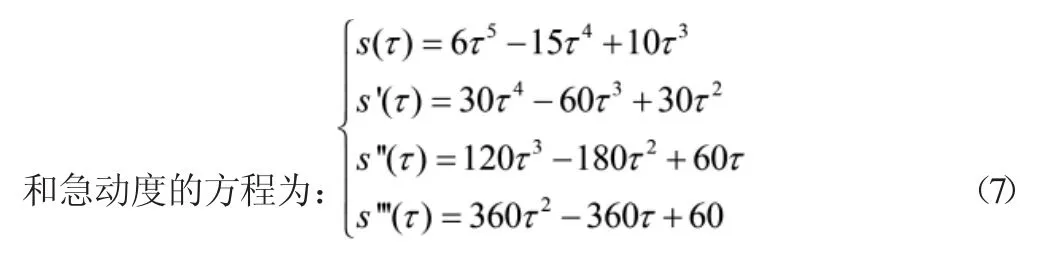
在碼垛機器人運動過程中，位移如果產生突變，除不能完成既定任務外，工作空間會受到極大影響；速度如果產生突變，理論上加速度會無窮大，慣性力無窮大，產生剛性沖擊；加速度如果發(fā)生突變，亦會產生較大有限慣性力；急動度如果發(fā)生突變，會使機器人系統(tǒng)產生殘余振動。上述四種情形均會使碼垛機器人的運行性能變差，壽命降低，應力求避免發(fā)生，同時還應降低最大速度、最大加速度以及最大急動度的峰值。為了能夠直觀的對這四種函數曲線的各項運動性能進行對比以及選出運動性能相對優(yōu)良的函數曲線，如圖2所示。為了進一步降低碼垛機器人在運行過程中的最大速度和最大加速度的峰值，將加速度函數為正弦函數、余弦函數、線性函數和三次多項式函數放在同一個圖中進行比較，其中正弦函數和余弦函數圖像是重合的。從圖2（a）可以得出，4條曲線都是連續(xù)平緩的，沒有突變發(fā)生；從圖2（b）中可以得出，只有線性函數在行程的終止位置存在突變，有較大剛性沖擊，從速度的峰值考慮線性函數的速度峰值最大，其次是正弦函數、余弦函數和三次多項式函數，三者速度峰值差別不大；從圖2（c）中可以得出，線性函數在行程終止位置發(fā)生突變，伴有柔性沖擊，從加速度峰值的角度考慮線性函數最大，其次是正弦函數、余弦函數和三次多項式函數，三者加速度峰值很接近；從圖2（d）中可以得出，4條曲線均存在突變，其中線性函數急動度峰值最小，其次是正弦函數和余弦函數，最大為三次多項式函數，較其余三條曲線峰值大很多。因此綜合考慮軌跡規(guī)劃曲線的各項特征指標，選擇正弦函數或者余弦函數作為優(yōu)良曲線，文中將針對正弦函數進行深入研究。

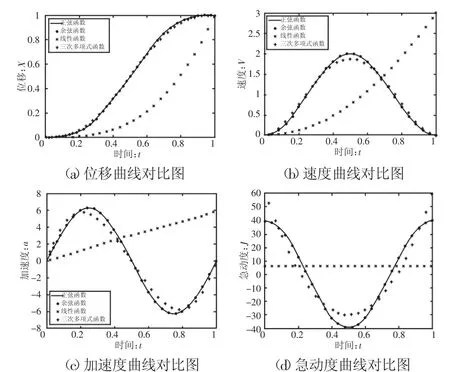
圖2 四條函數曲線的性能比較圖Fig.2 Performance Comparison of Four Function Curves Diagram

3 三段修正正弦函數法的軌跡規(guī)劃

由三條部分正弦曲線S1、S2和S3的組合而成，其中S1和S3是周期的正弦曲線，而S2是周期的正弦曲線，如圖3所示。該修正函數周期設為1，則S1、S3的周期為T1=T3=4/a，S2的周期為T2=2-4/a，頻率 ω1=ω3=aπ/2，ω2=aπ（/a-1）。考慮到修正的目的，修正參數a應該滿足∈（0，），即 a∈（2，+∞）。

圖3 三段修正正弦函數曲線圖Fig.3 Three Stage Modified Sine Function Curve Diagram

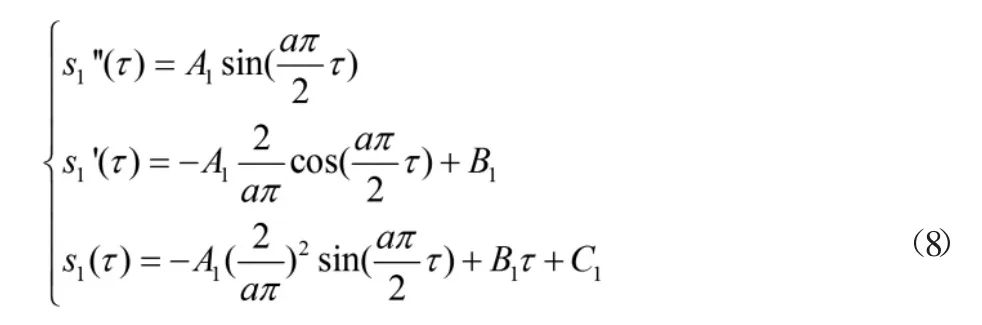
設第一段部分正弦曲線S1方程為：經推理第二段部分正弦曲線S2可以由正弦曲線S1先伸長倍，再向左平移得到，因此可以設正弦曲線S2的方程為：

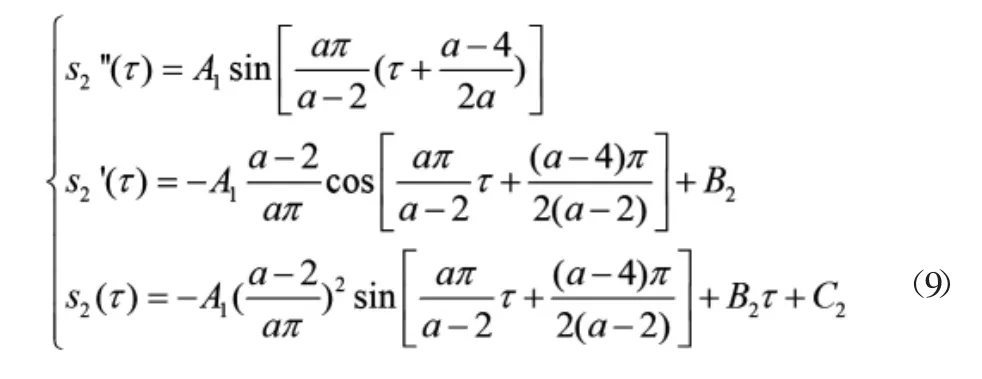
經推理第三段部分正弦曲線S3可以由正弦曲線S1向右平移得到，因此設正弦曲線S的方程為：3

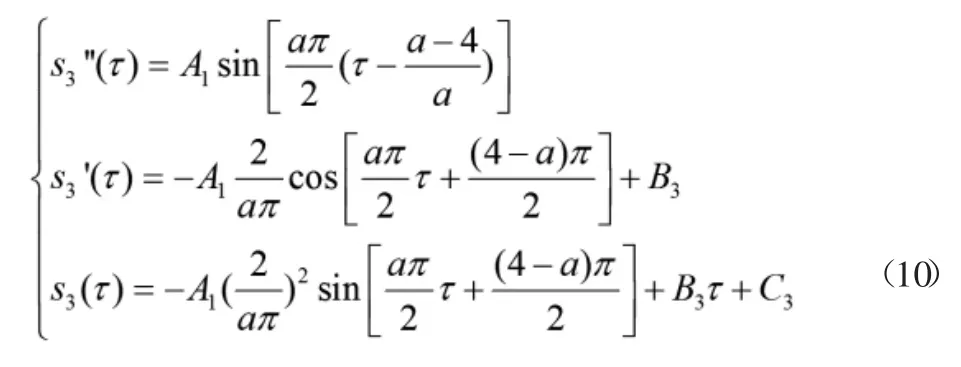
為了保證修正正弦曲線的連續(xù)性，在兩條曲線的交點處應保持數值相等，同時還要滿足初始條件，則有：

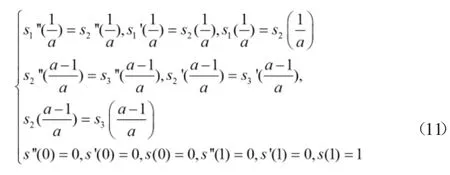
由公式計算可以得到修正正弦函數加速度曲線方程為：

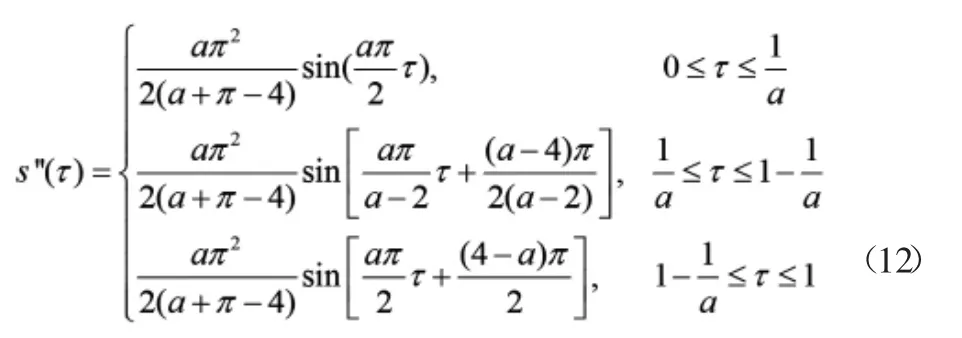
由公式計算可以得到修正正弦函數速度曲線方程為：

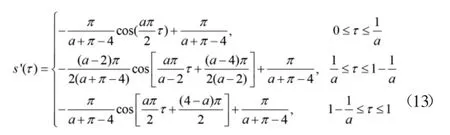
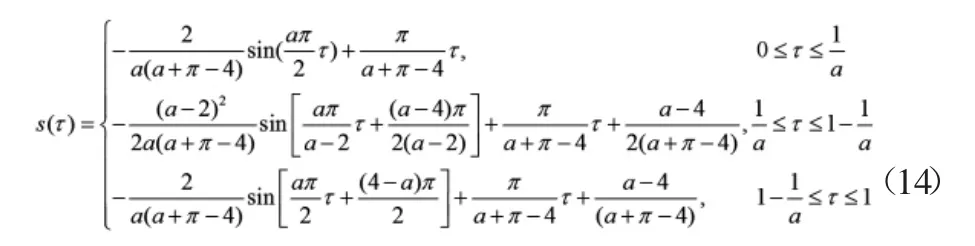
由公式計算可以得到修正正弦函數位移曲線方程為：由公式計算可以得到修正正弦函數急動度曲線方程為：

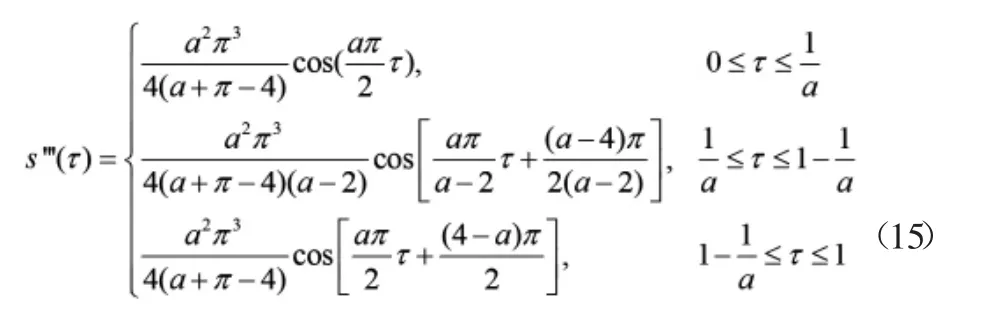
4 基于遺傳算法的多目標優(yōu)化

4.1 目標函數的確定

為了解決多目標優(yōu)化問題，本優(yōu)化采用統(tǒng)一目標函數法中的目標規(guī)劃法把多目標優(yōu)化問題轉化為單目標優(yōu)化問題。目標規(guī)劃法是一種相對較簡潔的構造統(tǒng)一目標函數的方法，首先確定各目標函數在最優(yōu)解時的最優(yōu)函數值，然后再根據多目標問題的總體要求對這些最優(yōu)值做出相應調整，最后確定各個目標的最優(yōu)值fj（j=0，1，2，…，n），因此所構造的統(tǒng)一目標函數為：

在本優(yōu)化模型中，當a趨近無窮大時，最大加速度取得最小值，即；當a趨近無窮大時，最大速度取得最小值，即f2=經過計算，當a=4時，最大急動度取得最小值，即f3=4π2，因此統(tǒng)一量綱之后的目標函數可以表示為：

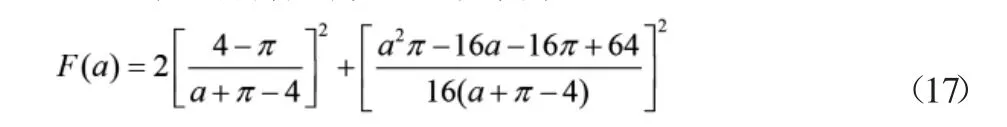
其中，修正參數a∈（2，+∞）。

4.2 遺傳算法工具箱的參數設置

（1）對適應度函數進行編程，命名為my_fit；（2）設置算法參數，設置 Solver為ga-GeneticAlgorithm，Fitnessfunction為@my_fit，Number of variable為1，為防止算法陷入局部解并有較高的運算速度，設置Populationsize為 50，CrossoverFraction 為0.85，Migration Fraction 為 0.2[10]；（3）選取需要繪制的圖像如 Generation，Bestindividual等。

4.3 優(yōu)化結果分析

經Matlab遺傳算法工具箱的優(yōu)化運算，返回的最佳修正參數和目標函數值為：Best a=4.735，Best Fval=0.1164，經過57代的遺傳運算得到的優(yōu)化結果圖，如圖4所示。將通過Matlab遺傳算法工具箱得到的最優(yōu)修正參數a=4.735分別帶入到公式中，比較三段修正正弦加速曲線與普通正弦加速曲線的位移曲線、速度曲線、加速度曲線和急動度曲線的運動性能。

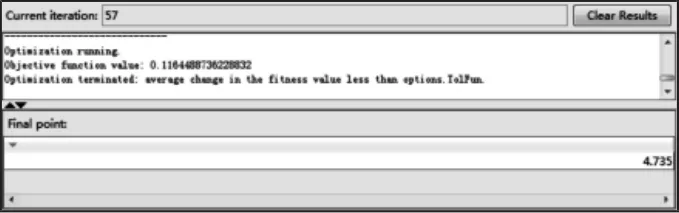
圖4 遺傳算法優(yōu)化效果圖Fig.4 Effect of Genetic Algorithm Optimization Diagram

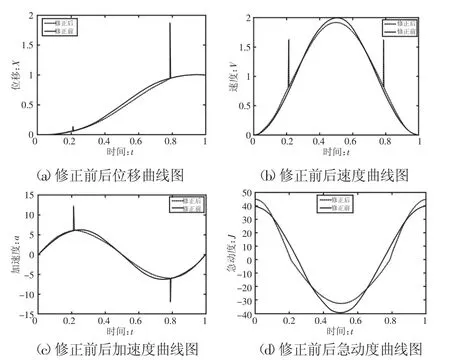
圖5 修正正弦函數和正弦函數性能對比圖Fig.5 Comparison of the Performance of Modified Sine Function and Sine Function Diagram

從5（a）中可以看出，加速正弦函數曲線修正后較修正前，位移變化的更光滑平緩，修正前后的位移均未出現突變；從5（b）中可以看出，修正后的正弦加速曲線的速度與修正前同時達到峰值，但修正后的峰值明顯降低，能有效提高碼垛機器人的運動性能；從中5（c）可以看出，修正后的正弦加速曲線的加速度較修正前提前達到峰值，而且修正后的加速度峰值略有降低，提高了碼垛機器人的動態(tài)性能；從5（d）中可以看出，在行程的始末位置正弦加速曲線修正前后均出現較大的突變，但是文中涉及的碼垛機器人是輕量中速的，主要對速度和加速度要求較高，急動度的影響相對較小。表1清楚明了的顯示了三段修正正弦法的修正效果。從表中容易看出，三段修正正弦函數曲線較正弦函數曲線的速度峰值降低了4.09%，加速度峰值亦降低了4.09%，但急動度峰值升高了12.002%。急動度表示加速度的變化快慢，在高速重載工況下，如果碼垛機器人的急動度較大且在運行過程中存在頻繁的啟停和變化，會導致相應零件發(fā)生磨損和振動，甚至可能引起頻跳造成受力不均勻、沖擊過大和疲勞斷裂等問題，所以三段修正正弦法適用于輕載中速的工況，在高速重載的工況下，應該注意適當降低急動度峰值。

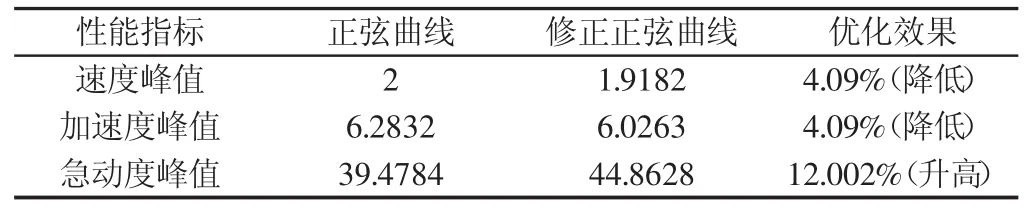
表1 正弦加速曲線修正前后的性能比較表Tab.1 Comparison of the Performance Before and After the Correction of the Sine Acceleration Curve

5 結論

（1）通過比較加速度函數為線性函數、三次多項式函數、正弦函數和余弦函數的特性曲線，發(fā)現正弦函數的綜合運動性能最佳，既無剛性沖擊也無柔性沖擊，而且不存在位置突變。（2）提出了一種三段修正正弦函數的軌跡規(guī)劃算法，在關節(jié)空間對碼垛機器人的運動軌跡進行規(guī)劃，然后利用遺傳算法工具箱以速度峰值、加速度峰值和急動度峰值為目標進行多目標參數優(yōu)化，得到最佳的修正參數。結果表明，三段修正正弦函數曲線的速度峰值降低了4.09%，加速度峰值亦降低了4.09%，提高了碼垛機器人的運動平穩(wěn)性和運動精度、減少了振動和沖擊，延長了碼垛機器人的使用壽命。