3-RRP平面并聯(lián)機(jī)構(gòu)的動(dòng)力學(xué)性能研究

李 虹，劉小娟，李瑞琴

（中北大學(xué) 機(jī)械與動(dòng)力工程學(xué)院，山西 太原 030051）

1 引言

三自由度平面并聯(lián)機(jī)構(gòu)是并聯(lián)機(jī)構(gòu)的重要分支，其結(jié)構(gòu)簡(jiǎn)單，制造加工成本低，易于實(shí)現(xiàn)精確的運(yùn)動(dòng)控制[1-2]。近年來(lái)許多學(xué)者對(duì)其進(jìn)行研究。文獻(xiàn)[3-4]對(duì)3-RRP球面并聯(lián)機(jī)構(gòu)利用牛頓-歐拉法建立機(jī)構(gòu)動(dòng)力學(xué)模型，求解動(dòng)力學(xué)方程，進(jìn)行動(dòng)力學(xué)分析。文獻(xiàn)[5]基于BP神經(jīng)網(wǎng)絡(luò)算法對(duì)3-RRP平面并聯(lián)機(jī)構(gòu)建立神經(jīng)網(wǎng)絡(luò)模型，求解出該機(jī)構(gòu)的位置正解。文獻(xiàn)[6]對(duì)3-PRR并聯(lián)機(jī)構(gòu)采用拉格朗日方程建立機(jī)構(gòu)的修正動(dòng)力學(xué)方程并結(jié)合實(shí)例分析，利用仿真驗(yàn)證模型的正確性。文獻(xiàn)[7]在考慮摩擦和無(wú)摩擦的兩種情形下對(duì)3-PPR平面并聯(lián)機(jī)構(gòu)進(jìn)行機(jī)構(gòu)動(dòng)力學(xué)研究。

目前，國(guó)內(nèi)外對(duì)3-RRP并聯(lián)機(jī)構(gòu)的運(yùn)動(dòng)學(xué)分析及仿真有一定的研究。對(duì)3-RRP平面并聯(lián)機(jī)構(gòu)進(jìn)行動(dòng)力學(xué)研究，采用虛功原理進(jìn)行動(dòng)力學(xué)求解。其中虛功原理[8-9]是用旋量表示機(jī)構(gòu)方程中的力和力矩。并采用ADAMS對(duì)該機(jī)構(gòu)進(jìn)行動(dòng)力學(xué)仿真，對(duì)精確控制機(jī)構(gòu)運(yùn)動(dòng)具有重要意義，為機(jī)構(gòu)的實(shí)際應(yīng)用提供理論依據(jù)。

2 3-RRP平面并聯(lián)機(jī)構(gòu)的構(gòu)型描述

3-RRP平面并聯(lián)機(jī)構(gòu)簡(jiǎn)圖，如圖1所示。3-RRP平面并聯(lián)機(jī)構(gòu)由動(dòng)平臺(tái)和靜平臺(tái)以及三條支鏈（兩個(gè)轉(zhuǎn)動(dòng)副與一個(gè)移動(dòng)副聯(lián)接而成）組成，三條支鏈對(duì)稱分布。如圖1，動(dòng)平臺(tái)為正三角形D1D2D3，該平臺(tái)通過(guò)移動(dòng)副P(pán)i與轉(zhuǎn)動(dòng)副Ci相連，轉(zhuǎn)動(dòng)副Bi通過(guò)連桿BiCi相連。

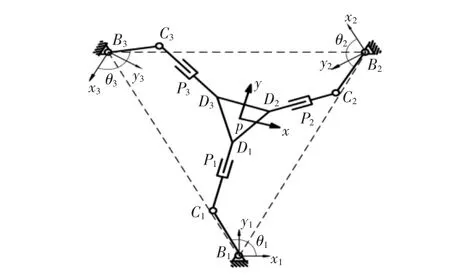
圖1 3-RRP平面并聯(lián)機(jī)構(gòu)簡(jiǎn)圖Fig.1 Diagram of 3-RRP Planar Parallel Mechanism

采用Kutzbach-Grubler法來(lái)計(jì)算該并聯(lián)機(jī)構(gòu)自由度公式如下：

式中：M—機(jī)構(gòu)的自由度；

d—機(jī)構(gòu)階數(shù)，d=3；

n—總的構(gòu)件數(shù)目，n=8；

g—整個(gè)機(jī)構(gòu)總的運(yùn)動(dòng)副數(shù)，g=9；

由上式（1）可得M=3，即3-RRP平面并聯(lián)機(jī)構(gòu)的自由度數(shù)是3。與機(jī)架相連的三個(gè)轉(zhuǎn)動(dòng)副作為機(jī)構(gòu)的驅(qū)動(dòng)輸入。

3 3-RRP平面并聯(lián)機(jī)構(gòu)奇異性分析

奇異位形[10]定義為：機(jī)構(gòu)在運(yùn)動(dòng)過(guò)程中，出現(xiàn)一些特殊的位置，如機(jī)構(gòu)處于死點(diǎn)，不能連續(xù)運(yùn)動(dòng)、運(yùn)動(dòng)不穩(wěn)定，甚至其自由度發(fā)生變化等；且一些機(jī)構(gòu)還出現(xiàn)受力狀態(tài)改變，導(dǎo)致機(jī)構(gòu)的各項(xiàng)運(yùn)動(dòng)性能變差，使得機(jī)構(gòu)的傳遞運(yùn)動(dòng)和動(dòng)力能力失常，進(jìn)而有可能損壞機(jī)構(gòu)。上述情況會(huì)將影響機(jī)構(gòu)的正常工作，在對(duì)機(jī)構(gòu)進(jìn)行軌跡規(guī)劃時(shí)，應(yīng)該避開(kāi)機(jī)構(gòu)的奇異位形。

3.1 3-RRP平面并聯(lián)機(jī)構(gòu)雅克比矩陣求解

當(dāng)機(jī)構(gòu)在奇異位置時(shí)，機(jī)構(gòu)的雅可比矩陣變成奇異矩陣，其判別方法與線性代數(shù)中矩陣判別方法一致，通過(guò)計(jì)算矩陣是否滿秩或行列式的值是否為0進(jìn)行判斷。機(jī)構(gòu)的雅可比矩陣對(duì)機(jī)構(gòu)運(yùn)動(dòng)特性的研究至關(guān)重要。

以下進(jìn)行求解3-RRP平面并聯(lián)機(jī)構(gòu)雅克比矩陣。

如圖1所示，動(dòng)平臺(tái)三角形幾何中心為點(diǎn)p，建立動(dòng)坐標(biāo)系p-xy，設(shè)轉(zhuǎn)動(dòng)副初始角為α1，α2，α3，三個(gè)轉(zhuǎn)動(dòng)輸入角參數(shù)為θi（i=1，2，3），動(dòng)平臺(tái)輸出位姿參數(shù)（xp，yp，αp）。

如下為3-RRP平面并聯(lián)機(jī)構(gòu)的運(yùn)動(dòng)學(xué)方程：

式中：M和O—機(jī)構(gòu)輸入、輸出雅克比矩陣；

θ˙—驅(qū)動(dòng)角轉(zhuǎn)動(dòng)輸入速度。

3-RRP并聯(lián)機(jī)構(gòu)雅克比矩陣為：

3.2 3-RRP平面并聯(lián)機(jī)構(gòu)奇異位形求解

并聯(lián)機(jī)構(gòu)的奇異位形分類方式有很多，其中，按照機(jī)構(gòu)運(yùn)動(dòng)狀態(tài)分為：位移奇異、死點(diǎn)奇異、剩余自由度奇異、瞬時(shí)幾何奇異和自由度瞬時(shí)變化奇異。

由機(jī)構(gòu)的一般輸入輸出關(guān)系式：

JI—機(jī)構(gòu)輸入雅可比矩陣；

JE—機(jī)構(gòu)輸出雅可比矩陣。

對(duì)3-RRP平面并聯(lián)機(jī)構(gòu)采用上式（7）來(lái)判斷該機(jī)構(gòu)的奇異位形，故機(jī)構(gòu)奇異位形分為位形奇異、邊界奇異和結(jié)構(gòu)奇異。將由上述得到 Ei，F(xiàn)i，Gi，Ni代入式（3）可得機(jī)構(gòu)的奇異位形判別式，通過(guò)矩陣行列式的判別方法得到機(jī)構(gòu)的奇異位置。

（1）對(duì)于該機(jī)構(gòu)的輸入矩陣M，當(dāng)矩陣M行列式有為0時(shí)，此時(shí)機(jī)構(gòu)處在邊界奇異，則矩陣M中N1，N2，N3必有一個(gè)是0，（即當(dāng)動(dòng)平臺(tái)位姿角與輸入角相等且為0時(shí)，機(jī)構(gòu)發(fā)生邊界奇異）。這種奇異位置通常發(fā)生在運(yùn)動(dòng)空間邊界處，容易避免。

（2）對(duì)于機(jī)構(gòu)的輸出矩陣O，當(dāng)其行列式值有為0時(shí)，此時(shí)機(jī)構(gòu)處在位形奇異（發(fā)生這種情況時(shí)，機(jī)構(gòu)剛度性能發(fā)生改變，動(dòng)平臺(tái)將無(wú)法承受任何受力，將影響機(jī)構(gòu)的運(yùn)動(dòng)性能。）當(dāng)矩陣O中任意一列為0，則矩陣O的行列式值為0；其中矩陣O的第一列和第二列分別為該機(jī)構(gòu)的三條支鏈在x軸，y軸的投影。可以判斷矩陣O不存在行列式為0的情況。即3-RRP平面并聯(lián)機(jī)構(gòu)不存在位形奇異。

（3）由上面的式（6）來(lái)判斷該機(jī)構(gòu)的雅克比矩陣J，其不存在行列式為0的情形。

所以由上述分析可得3-RRP平面并聯(lián)機(jī)構(gòu)只存在一個(gè)奇異位形，為邊界奇異位形。其情形，如圖2所示。

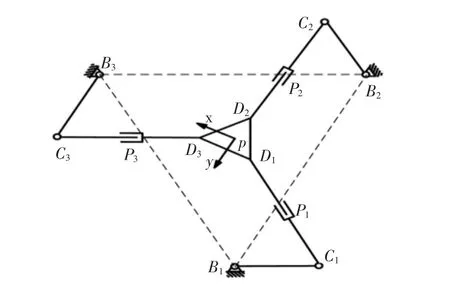
圖2 3-RRP平面并聯(lián)機(jī)構(gòu)的奇異位形Fig.2 Singular Configuration of 3-RRP Planar Parallel Mechanism

4 3-RRP平面并聯(lián)機(jī)構(gòu)動(dòng)力學(xué)建模

建立如圖3所示的動(dòng)力學(xué)模型簡(jiǎn)圖，設(shè)BiCi段用向量表示，CiDi段用向量表示，中心點(diǎn)p與三角形三個(gè)頂點(diǎn)連線的向量為，三個(gè)轉(zhuǎn)動(dòng)副的輸入為驅(qū)動(dòng)角θi（其中，i=1，2，3）。

下面采用虛功原理對(duì)3-RRP平面并聯(lián)機(jī)構(gòu)進(jìn)行動(dòng)力學(xué)數(shù)學(xué)建模，根據(jù)圖3列出3-RRP。

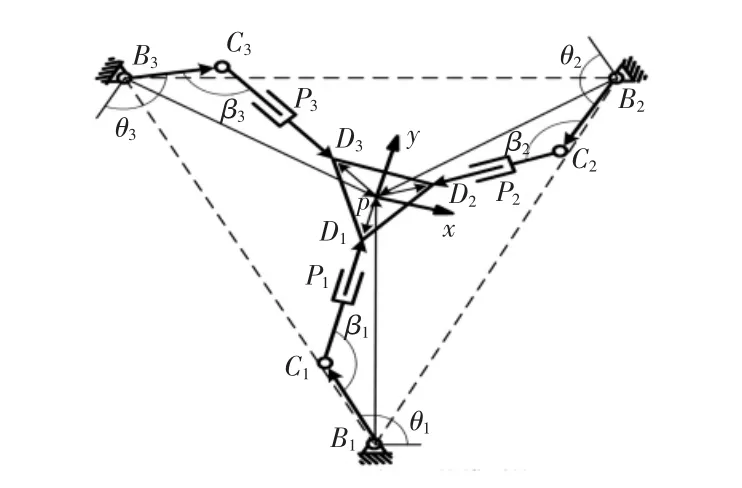
圖3 3-RRP平面并聯(lián)機(jī)構(gòu)模型簡(jiǎn)圖Fig.3 Model Diagram of 3-RRP Planar Parallel Mechanism

對(duì)式（8）兩邊對(duì)時(shí)間t求導(dǎo)可得：

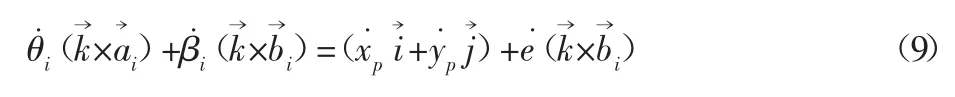
將式（9）兩邊同乘b→i可得：

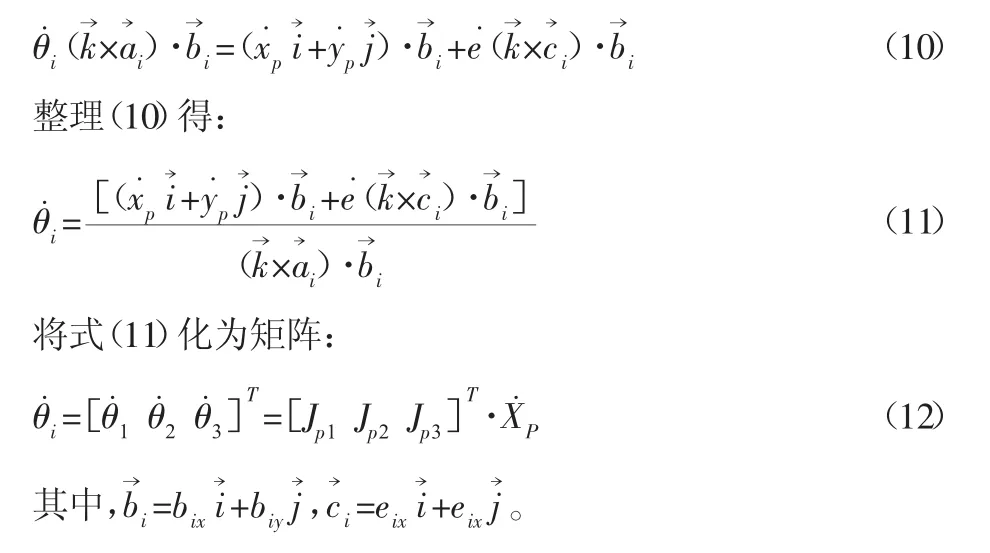
平面并聯(lián)機(jī)構(gòu)各條支鏈的向量表達(dá)形式為：

再將式（12）兩邊同乘a→i得出機(jī)構(gòu)中各連桿的角速度為：

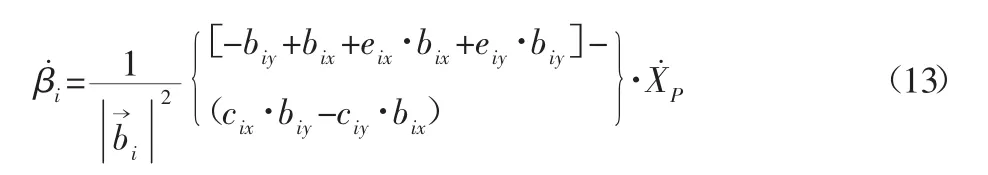
將式（13）化為矩陣如下：

由式（14）和式（15）可求出該機(jī)構(gòu)的速度。對(duì)所求得的速度表達(dá)式對(duì)其求導(dǎo)，得到加速度表達(dá)式為：

對(duì)式（17）化簡(jiǎn)，得各連桿角加速度為：

同時(shí)可得出各連桿加速度方程為：

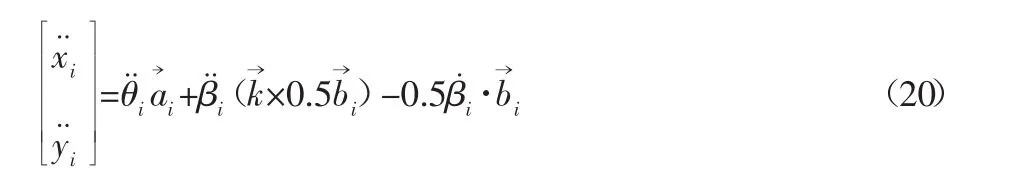
通過(guò)以上求得連桿與動(dòng)平臺(tái)的速度、加速度，采用虛功原理求該機(jī)構(gòu)所受到的外力，三個(gè)驅(qū)動(dòng)副的轉(zhuǎn)動(dòng)驅(qū)動(dòng)力，連桿的移動(dòng)慣量，可得出如下方程：

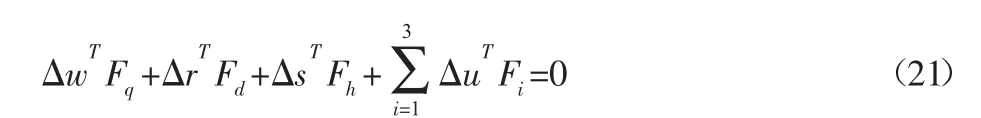
式中：Δw—驅(qū)動(dòng)副的虛位移；Δr—?jiǎng)悠脚_(tái)的虛位移；Δs—滑塊的虛位移；Δu—連桿的虛位移；wq—驅(qū)動(dòng)力矩；Fd、Fh、Fi、Fq—各質(zhì)點(diǎn)的慣性矢量。

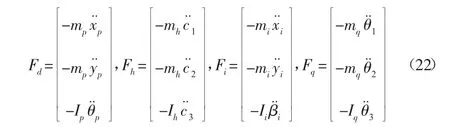
把式（12）、式（13）代入式（21）中得到機(jī)構(gòu)動(dòng)力學(xué)逆解方程為：

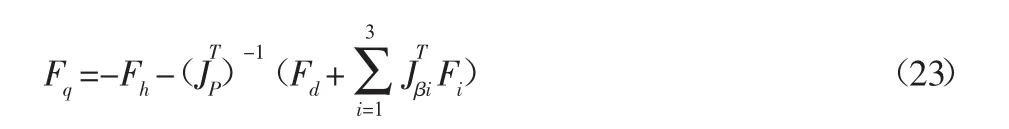
上述為研究3-RRP平面并聯(lián)機(jī)構(gòu)的動(dòng)力學(xué)方程求解。

5 ADAMS動(dòng)力學(xué)仿真

采用Pro/E軟件建立機(jī)構(gòu)模型，機(jī)構(gòu)驅(qū)動(dòng)桿BiCi段的長(zhǎng)度為58mm，CiDi段連桿的長(zhǎng)度為160mm，動(dòng)平臺(tái)D1D2D3的外接圓半徑e=75。2mm。將模型導(dǎo)入到ADAMS中，設(shè)置仿真環(huán)境，模型的重力方向?yàn)?，單位為MMKS，剛體材料為鋼結(jié)構(gòu)，密度ρ=7800kg/m3。添加運(yùn)動(dòng)約束，三驅(qū)動(dòng)桿上添加驅(qū)動(dòng)，動(dòng)平臺(tái)的中心為標(biāo)記點(diǎn)。如下分析動(dòng)平臺(tái)在不受外載荷和受到不同外載荷的作用下，動(dòng)平臺(tái)中心點(diǎn)運(yùn)動(dòng)軌跡為8字形，如圖4所示。三個(gè)驅(qū)動(dòng)電機(jī)的功率損耗情況。

圖4 動(dòng)平臺(tái)輸出端8字形曲線Fig.4 Output of the Dynamic Platform 8 Curve

動(dòng)平臺(tái)受不同外力載荷分別為：

（1）動(dòng)平臺(tái)不受外載荷；

（2）動(dòng)平臺(tái)受外載荷為80N的力；

（3）動(dòng)平臺(tái)受外載荷為120N的力；

（4）動(dòng)平臺(tái)受外載荷為150N的力。

上述的四種情況下動(dòng)平臺(tái)運(yùn)行8字形軌跡，在PostProcessor后處理中繪制出三個(gè)驅(qū)動(dòng)電機(jī)在不同載荷下的功率損耗，如圖5～圖7所示。

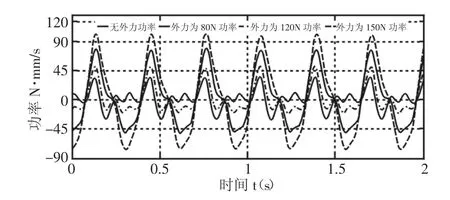
圖5 1號(hào)電機(jī)功率消耗Fig．5 Motor 1 Power Consumption

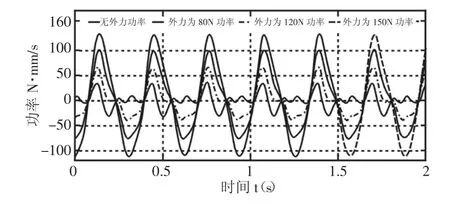
圖6 2號(hào)電機(jī)功率消耗Fig．6 Motor 2 Power Consumption

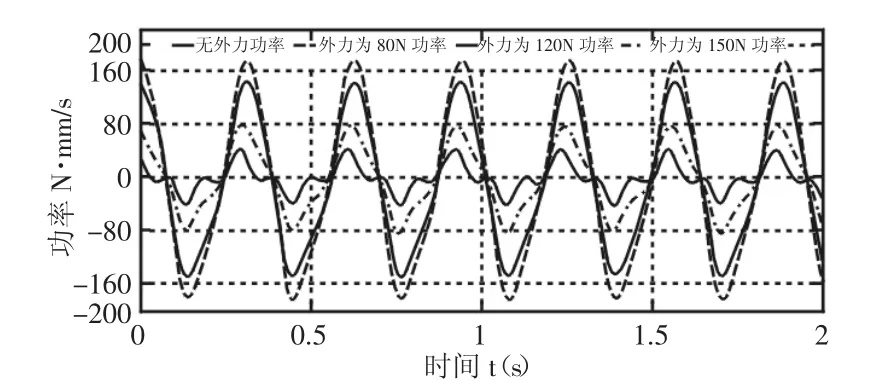
圖7 3號(hào)電機(jī)功率消耗Fig．7 Motor 3 Power Consumption

由上圖5～圖7所示，動(dòng)平臺(tái)中心點(diǎn)運(yùn)動(dòng)軌跡為8字形時(shí)，由于三個(gè)驅(qū)動(dòng)不同對(duì)應(yīng)電機(jī)損耗情況不同。三個(gè)驅(qū)動(dòng)電機(jī)功率出現(xiàn)峰值的時(shí)間相同且功率損耗隨動(dòng)平臺(tái)受到外載荷大小的增加而增加，其中，1號(hào)和2號(hào)電機(jī)隨時(shí)間變化功率損耗變化趨勢(shì)相同，而3號(hào)電機(jī)剛好相反。當(dāng)動(dòng)平臺(tái)外載荷為150N，1號(hào)電機(jī)最大損耗110N·mm/s，2號(hào)電機(jī)最大損耗140N·mm/s，3號(hào)電機(jī)最大損耗180N·mm/s。由對(duì)上圖的分析可得動(dòng)平臺(tái)不受載荷和受不同外載荷，3號(hào)電機(jī)功率損耗最大，1號(hào)電機(jī)功率損耗最小。

6 結(jié)論

（1）通過(guò)求機(jī)構(gòu)的雅克比矩陣和采用虛功原理對(duì)3-RRP平面并聯(lián)機(jī)構(gòu)求解出其的動(dòng)力學(xué)逆解方程。

（2）利用ADAMS動(dòng)力學(xué)仿真，動(dòng)平臺(tái)承載不同外載荷下，其末端中心點(diǎn)運(yùn)動(dòng)8字形軌跡時(shí)，分析三個(gè)驅(qū)動(dòng)電機(jī)功率損耗情況；得出隨外載荷的增加，3個(gè)電機(jī)功率是損耗曲線情況變化規(guī)律相似，功率損耗最大是3號(hào)電機(jī)，最小是1號(hào)電機(jī)。為3-RRP平面并聯(lián)機(jī)構(gòu)在實(shí)際應(yīng)用中的電機(jī)選擇提供重要的理論依據(jù)。

（3）3-RRP平面并聯(lián)機(jī)構(gòu)是一種3-DOF平面并聯(lián)機(jī)構(gòu)，適用于數(shù)控精密繡花機(jī)、微動(dòng)工作平臺(tái)等。因此對(duì)該機(jī)構(gòu)動(dòng)力學(xué)的研究，為更加精確的控制機(jī)構(gòu)運(yùn)動(dòng)具有重要意義。