傳感器尺寸對高速列車空氣動力學(xué)測試影響

何洪陽，陳麒天，陳春俊

（1.中國核動力研究設(shè)計院，四川 成都 610041；2.成都外國語學(xué)校，四川 成都 611731；3.西南交通大學(xué) 機(jī)械工程學(xué)院，四川 成都 610031）

1 引言

隨著列車的運(yùn)行速度不斷提高，空氣動力效應(yīng)加劇[1]。列車表面壓力分布不同而產(chǎn)生氣動載荷，氣動載荷直接影響列車的行車安全、能耗、氣動噪聲、氣動振動及車內(nèi)氣壓舒適性等[3-4]。因此，對列車表面壓力準(zhǔn)確測試至關(guān)重要，線路試驗是研究列車空氣動力學(xué)最直接的方法。為了減小傳感器自身尺寸對測點處流場的影響[4-5]，選取航空航天領(lǐng)域常用的貼片式微型超薄壓阻式氣壓傳感器。由于傳感器的體積小，通常線路試驗時忽略傳感器自身尺寸對測點流場影響。然而，傳感器自身尺寸對測點流場影響未知，需進(jìn)一步探究其測試誤差，以此來修正測試信號。

針對這一問題，以某CRH型高速列車為研究對象，在頭車側(cè)面中部某測點處建立含有傳感器的列車模型，在不同典型速度級下采用大渦數(shù)值模擬（Large Eddy Simulation，LES）方法數(shù)值仿真計算測點處的表面壓力，利用希爾伯特-黃變換提取出脈動壓力，并與無傳感器的單獨列車模型相同測點處的表面壓力相比較，建立由于傳感器自身尺寸帶來的測量誤差與運(yùn)行速度之間的函數(shù)關(guān)系。對線路試驗時列車表面壓力信號進(jìn)行修正，為高速列車氣動性能分析提供更準(zhǔn)確的試驗數(shù)據(jù)。

2 線路試驗測點處壓力

列車線路試驗時，通常將微型壓阻式壓力傳感器貼在車體表面，測試其測點處的壓力信號。列車表面壓力可分解為平均壓力和脈動壓力，前者形成平均載荷，后者形成脈動載荷[6]。由于傳感器自身尺寸影響，引起平均壓力和脈動壓力的測量誤差，并且測試壓力信號易受電磁溫度等隨機(jī)干擾。因此，測點處壓力信號可表示為：

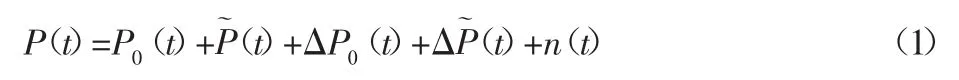
式中：P（t）—測點處壓力信號；P0（t）—平均壓力(t）—脈動壓力；ΔP0（t）—傳感器自身尺寸帶來的平均壓力測量誤差；Δ（t）—傳感器自身尺寸帶來的脈動壓力測量誤差；n（t）—電磁溫度等隨機(jī)干擾。

3 模型建立

3.1 列車簡化模型

以某CRH型高速列車為研究對象，頭尾車具有相同的形狀。為減小CFD的計算量，建立由頭車和尾車組成的列車計算模型，頭車長10．5m，寬 3．38m，高 3．7m，2節(jié)列車的簡化模型，如圖1所示。

受計算條件及動車組復(fù)雜外形的限制，在不影響計算精度的情況下，作如下假設(shè)：（1）當(dāng)列車以＞250km/h速度運(yùn)行時，以列車寬度為特征長度計算的雷諾數(shù)R＞106，流場處于湍流狀態(tài)，可采用大渦數(shù)值模擬和壁面函數(shù)模擬車體表面周圍的流場；（2）幾何模型建立時，認(rèn)為車體是一個具有光滑外形的幾何體，在一定程度上忽略輪軌系統(tǒng)、轉(zhuǎn)向架及懸架系統(tǒng)、門窗凸起部位和受電弓等。

圖1 列車簡化模型Fig．1 Train Simplified Model

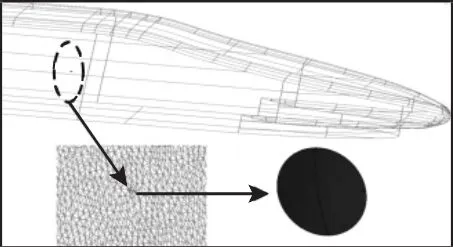
圖2 傳感器簡化模型Fig．2 Sensor Simplified Model

3.2 傳感器模型

列車表面壓力測試中，貼片式微型超薄壓阻式氣壓傳感器因為其體積小、重量輕、靈敏度高等優(yōu)點，被廣泛用于航空器和高速列車表面壓力測試。常用傳感器尺寸為直徑6．35mm，厚度0．76mm的圓片，在動車組車外表面壓力實際測試過程中，采用膠帶將傳感器粘貼于列車表面。因此，考慮膠帶粘貼后，傳感器測點在列車表面的形狀為上底面直徑8mm、下底面直徑30mm，高1mm的梯形圓柱。壓阻式氣壓傳感器的簡化模型，如圖2所示。

3.3 外流場模型

列車明線交會和通過隧道時，會在車體表面形成復(fù)雜的交會壓力波和隧道壓力波，難于從這些復(fù)雜壓力波提取脈動壓力。因此選取明線運(yùn)行工況，理論上外流場的計算區(qū)域應(yīng)該無限大，計算結(jié)果才能更接近真實值。然而外流場區(qū)域越大，其網(wǎng)格質(zhì)量增加，對計算機(jī)內(nèi)存及性能提出更高要求。

采用滑移網(wǎng)格技術(shù)實現(xiàn)車體運(yùn)動，整個計算區(qū)域分為外流場計算區(qū)域和滑移網(wǎng)格區(qū)域，含有車體的滑移網(wǎng)格區(qū)域以車體速度運(yùn)行，外流場區(qū)域保持靜止。不同區(qū)域間的數(shù)據(jù)交換通過交界面（interface）進(jìn)行。在不影響精度的基礎(chǔ)上縮小計算區(qū)域，將計算區(qū)域確定為[7]：列車寬度方向為車寬的10倍左右，高度方向為車高的15倍左右，運(yùn)行方向上的外流場尺寸要大于列車長度的20倍以上，整個計算區(qū)域長、寬、高分別為（323×44×30）m，同時將車體離地面的距離設(shè)置為0．2m。

4 數(shù)值仿真計算

4.1 網(wǎng)格生成及仿真設(shè)置

為了達(dá)到大渦數(shù)值模擬的精度，同時提高計算機(jī)的運(yùn)算速度，將滑移網(wǎng)格區(qū)域分為三部分：起始部分、車體部分及運(yùn)動方向部分，如圖3（a）所示。起始部分（長度取100m）和運(yùn)動方向部分（長度取250m）的結(jié)構(gòu)簡單、尺寸規(guī)則，采用六面體結(jié)構(gòu)網(wǎng)格技術(shù)，通過控制space ratio參數(shù)使靠近車體部分網(wǎng)格進(jìn)行適當(dāng)?shù)募用埽h(yuǎn)離車體部分網(wǎng)格較疏；車體部分由于高速列車模型較為復(fù)雜，采用四面體非結(jié)構(gòu)網(wǎng)格，車體表面設(shè)置10層網(wǎng)格加密，第一層網(wǎng)格厚度為0．4mm，鄰兩層邊界層網(wǎng)格保持1．5倍的增長比[7]，總厚度為57．7mm；外流場區(qū)域采用結(jié)構(gòu)化網(wǎng)格，靠近車體部分的計算區(qū)域網(wǎng)格加密，外流場區(qū)域網(wǎng)格總數(shù)約為540萬。最后將滑移網(wǎng)格區(qū)域和外流場區(qū)域合并在一起，生成湍流流場模擬的整個計算區(qū)域，網(wǎng)格總數(shù)約為1323萬，計算區(qū)域網(wǎng)格劃分的細(xì)節(jié)圖，如圖 3（b）所示。

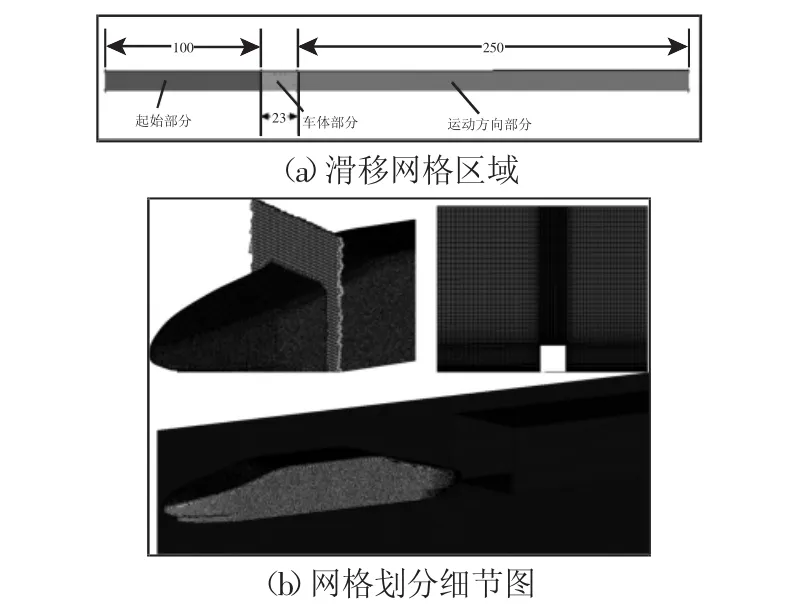
圖3 滑移網(wǎng)格區(qū)域及網(wǎng)格劃分細(xì)節(jié)圖Fig．3 Sliding Mesh Area and Details of Grids

設(shè)置地面及車體表面為無滑移壁面邊界（Wall），外流場區(qū)域選擇壓力邊界條件（Pressure-outlet），表面壓力設(shè)置為0Pa，外流場區(qū)域與滑移網(wǎng)格區(qū)域的交界面設(shè)置為Interface。主要仿真計算車體表面壓力及提取脈動壓力，選擇大渦數(shù)值模擬為湍流數(shù)值模擬方法、Smagorinsky-Lilly模型為亞格子模型，SIMPLE作為求解算法。采樣頻率 f取 10kHz，取（0．1～0．2）s之間數(shù)據(jù)進(jìn)行分析。

4.2 脈動壓力提取

選擇頭車為研究對象，在距離頭車8m的車體二位側(cè)表面中心位置建立如2．2節(jié)所述的傳感器模型，記傳感器位置處為測點A。單獨列車模型在測點處的表面壓力記為P0，含傳感器模型的列車模型在測點處壓力記為P1。同時在網(wǎng)格劃分時，對傳感器模型建立一個單獨Part，得到傳感器模型的上底面網(wǎng)格尺寸在1mm左右，相比于其直徑8mm來說，保證傳感器模型的網(wǎng)格質(zhì)量，避免網(wǎng)格質(zhì)量對計算結(jié)果帶來的影響。

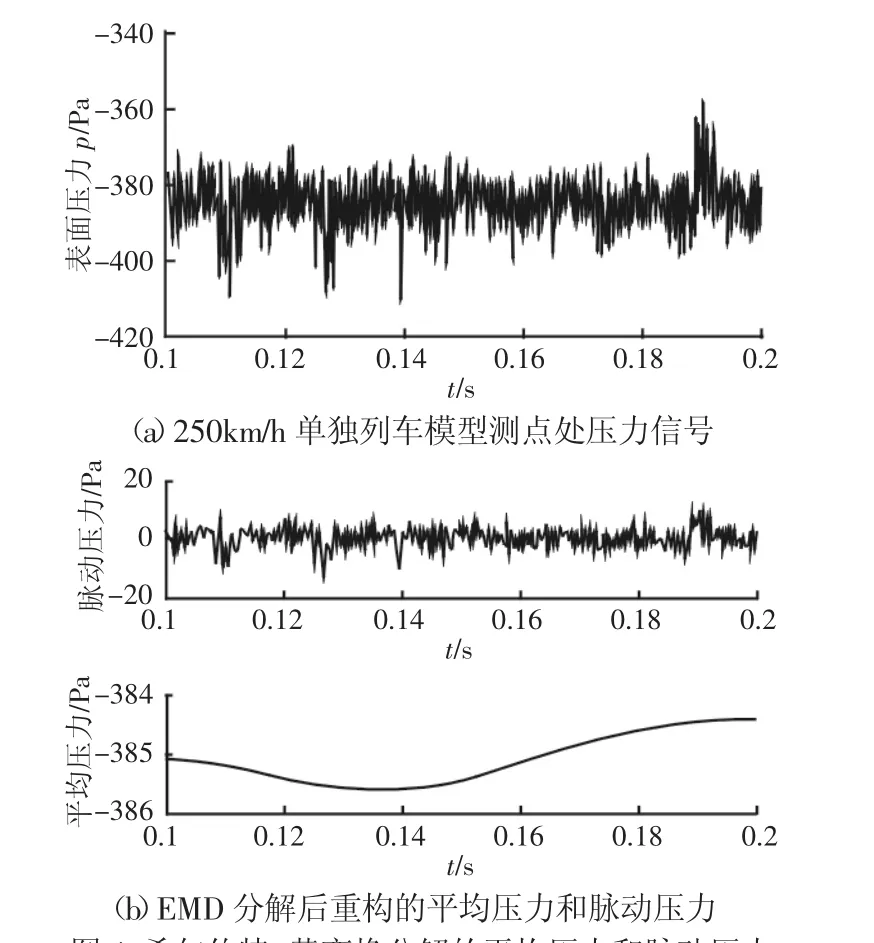
圖4 希爾伯特-黃變換分解的平均壓力和脈動壓力Fig．4 Mean Pressure and Fluctuation Pressure of Hilbert Huang Transform Decomposition

250km/h速度級下，單獨列車模型在測點處的表面壓力信號，如圖4（a）所示。可將P0視為測點處表面壓力的真值，可知表面壓力信號的幅值約為-380Pa，時域內(nèi)隨機(jī)波動±20Pa左右。

希爾伯特-黃變換[8]（Hilbert-Huang Transform，HHT）能將復(fù)雜信號自適應(yīng)地分解成多個單一分量，更深層次反應(yīng)信號內(nèi)部特征；常用于研究非平穩(wěn)、非線性的空氣湍流問題[9-10]。運(yùn)用希爾伯特-黃變換從列車表面壓力信號中提取脈動壓力。對信號進(jìn)行EMD分解，自適應(yīng)分解為9層，分別為IMF1～I(xiàn)MF8分量和余項r；每個IMF分量都有相應(yīng)的主頻，但各個頻段的幅值具有很大差異，本征函數(shù)的頻率從IMF1～I(xiàn)MF8逐漸減小，直到得到殘差函數(shù)。因此，余項r可視為平均壓力，其它IMF分量之和構(gòu)成脈動壓力。EMD分解及重構(gòu)后的平均壓力和脈動壓力，如圖4（b）所示。平均壓力幅值約為（-385）Pa，脈動壓力幅值約為（±20）Pa。

5 結(jié)果分析

5.1 對平均壓力影響

250km/h速度下，對含傳感器的列車模型進(jìn)行仿真計算，取測點處的壓力信號P1，并與理論真值P0相比較。由于傳感器自身尺寸影響，導(dǎo)致測點處表面壓力由（-385）Pa減小到（-425．5）Pa左右，可知傳感器自身尺寸對車體表面壓力影響極大。同理，采用大渦數(shù)值模擬方法計算在300km/h、350km/h速度下單獨列車模型和含傳感器的列車模型在測點處的表面壓力，并求解其測量誤差的絕對值ΔP，如表1所示。

用冪函數(shù)擬合測量誤差絕對值ΔP與運(yùn)行速度v之間的函數(shù)關(guān)系為 ΔP=a×vb，其中參數(shù) a=3．697×10-3，b=1．687。可知隨列車運(yùn)行速度v增大，引起的測量誤差絕對值ΔP也增大，測量誤差絕對值ΔP近似與運(yùn)行速度v呈二次函數(shù)關(guān)系。

表1 測量誤差絕對值與運(yùn)行速度關(guān)系Tab.1 Relationship Between Absolute Value of Measurement Error and Running Speed

5.2 對脈動壓力影響

在250km/h、300km/h和350km/h速度級下，運(yùn)用希爾伯特-黃變換從車體表面壓力信號提取脈動壓力信號。脈動壓力和聲壓之間存在著對應(yīng)關(guān)系，根據(jù)式（2）求出測點處脈動壓力級（PFL），并通過快速傅里葉變換將脈動壓力時域轉(zhuǎn)化到頻域。各速度級下脈動壓力級波動范圍及波動幅度，如表2所示。

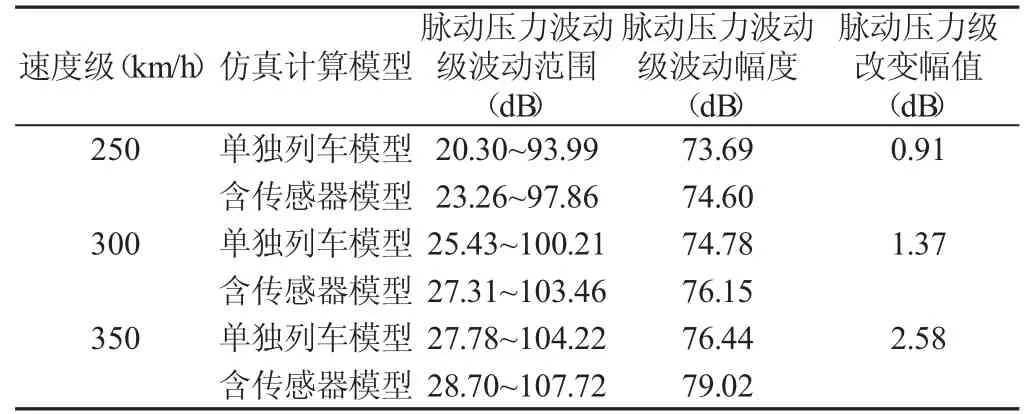
表2 各速度級下脈動壓力級波動范圍及波動幅度Tab.2 Wave Range and Amplitude of Fluctuation Pressure Level at Different Speeds

式中：p0—基準(zhǔn)壓力（為2×10-5Pa）；psf（y，t）—測點計算脈動壓力值。

各速度級下脈動壓力級具有寬頻特性，可用負(fù)指函數(shù)擬合在整個頻段內(nèi)的變化規(guī)律，低頻處幅值較大，而高頻處幅值較小；由于傳感器自身尺寸影響，測點處脈動壓力幅值大于真值，如表2所示。同理用冪函數(shù)擬合脈動壓力級改變幅值ΔPPFL與運(yùn)行速度 v 的冪函數(shù)關(guān)系，即 ΔPPFL=1．368×10-7×v2．835，即脈動壓力級改變幅值ΔPPFL與運(yùn)行速度v的三次方近似成正比。

實際工程試驗時由于采樣頻率限制，僅能測量某特定頻率段的車體表面壓力。在計算脈動壓力級的基礎(chǔ)上，推導(dǎo)出總脈動壓力級L的數(shù)學(xué)表達(dá)式：

式中：Li—頻率i處的脈動壓力級。

計算各速度級下單獨列車模型和含傳感器的列車模型在測點處脈動壓力的總脈動壓力級，如表3所示。可知含傳感器的列車模型測點的總脈動壓力級比理論真值較大；且隨速度增大其總脈動壓力級L增大，然而由于傳感器自身尺寸引起的總脈動壓力級改變幅值ΔL幾乎相等。

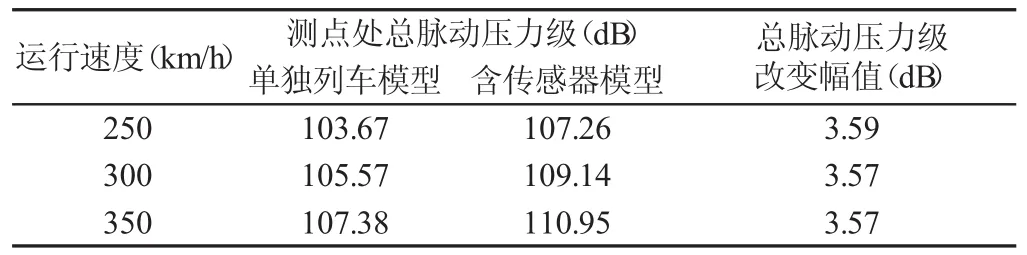
表3 各速度級下測點處總脈動壓力級Tab.3 Total Pressure Fluctuation Level at Different Speeds

6 結(jié)論

針對高速列車表面壓力測試過程中，傳感器自身尺寸會對測點處流場產(chǎn)生影響，導(dǎo)致測試的平均壓力和脈動壓力結(jié)果不準(zhǔn)確。建立含傳感器模型的列車模型，利用商業(yè)軟件FLUENT進(jìn)行大渦數(shù)值模擬，利用希爾伯特-黃變換提取脈動壓力；并與單獨列車模型相同測點處的壓力值進(jìn)行比較，分析傳感器自身尺寸帶來的測量誤差，并建立與運(yùn)行速度的冪函數(shù)關(guān)系。得出如下結(jié)論：

（1）由于傳感器自身尺寸影響，測點處的平均壓力絕對值遠(yuǎn)大于理論真值，且隨運(yùn)行速度增大其絕對誤差也增大；且測量誤差與運(yùn)行速度關(guān)系為：ΔP=3.697×10-3×v1.687，即近似與運(yùn)行速度呈二次函數(shù)關(guān)系；

（2）傳感器自身尺寸導(dǎo)致測點處的脈動壓力值偏大，脈動壓力級改變幅值ΔPPFL與運(yùn)行速度v的冪函數(shù)關(guān)系：ΔPPFL=1.368×10-7×v2.835；但各速度級下總脈動壓力級改變幅值幾乎相等。

傳感器自身尺寸會改變測點處湍流流場，導(dǎo)致測試結(jié)果不準(zhǔn)確。利用上述建立的冪函數(shù)關(guān)系式可修正測試數(shù)據(jù)，進(jìn)而為空氣動力學(xué)測試及性能分析提供更準(zhǔn)確的試驗數(shù)據(jù)。