慣性圓錐破碎機主軸的動力學特性分析

周弘揚，王春雨，鞏云鵬

（東北大學 機械工程與自動化學院，遼寧 沈陽 110819）

1 引言

慣性圓錐破碎機是一種具有物料選擇性的細碎破碎機。它與標準圓錐破碎機相比耗能更低，效率更高，因此被廣泛應用于冶金、礦山、建材等行業。

然而，在慣性圓錐破碎機的故障中，主軸斷裂是非常嚴重的。一旦發生斷裂，其維修成本很高，從而對企業造成較大的經濟損失。為了確保慣性圓錐破碎機安全、可靠運行，對主軸進行靜強度分析十分重要[1]。

在國內圓錐破碎機主軸的力學研究中，文獻[2]對彈簧式圓錐破碎機主軸進行了受力分析。通過主軸上的偏心軸套給主軸下端的反力對懸掛中心的力矩與破碎力、球面瓦給動錐的支持力對懸掛中心的合力矩的平衡計算出主軸所受到的力。文獻[3]對彈簧式圓錐破碎機主軸的受力采用幾何計算方法利用主軸上的偏心軸套給主軸下端的反力與破碎力、球面瓦對動錐的支持力三力平衡對主軸受力進行了分析。文獻[4]利用ANSYS分析軟件，將慣性圓錐破碎機的動錐、動錐襯板和主軸作為一體建模，將單位破碎力施加在動錐襯板上間接對主軸的進行力學分析。這些文獻中少有對慣性圓錐破碎機主軸進行直接的受力分析。

通過計算激振力得到慣性圓錐破碎機的最大破碎力，進而計算出最大破碎力引起的激振器對主軸最大作用力，對慣性圓錐破碎機主軸受力進行了直接的分析。最后，使用ANSYS APDL分析軟件對慣性圓錐破碎機主軸進行靜力學分析與模態分析，以期為其主軸的設計提供一定依據。

2 慣性圓錐破碎機的原理及特點

慣性圓錐破碎機機體安裝在隔振裝置上，破碎元件主要由定錐和動錐組成，動錐與定錐上安裝有耐磨襯板，動錐襯板與定錐襯板之間形成破碎腔。主軸上端與動錐相連，主軸下端通過軸套與偏心激振器相接。電動機旋轉通過傳動機構帶動固定在軸套上的偏心激振器，偏心激振器旋轉產生激振力，激振力通過主軸傳遞給動錐，使動錐繞球面瓦作球心運動。當破碎腔內有物料時，動錐伴有強烈的高頻振動，對物料進行沖擊、擠壓以此來破碎物料。當破碎腔內落入不可破碎物體時，由于動錐主軸與偏心激振器之間無剛性連接，雖然動錐被不可破碎的物料卡住而停止運動，但偏心激振器會繼續轉動，不會發生傳動系統的破壞。

具有料層選擇性是慣性圓錐破碎機相比于普通圓錐破碎機的重要特點。由于慣性圓錐破碎機沿物料晶格方向破碎，所以破碎力大，破碎效率更高，而且可以破碎硬度更大的物料。慣性圓錐破碎機安裝在二次隔振裝置上，不與大地相連，工作噪音小，操作安裝拆卸更方便。

3 主軸的受力分析

3.1 最大破碎力的計算

慣性圓錐破碎機的破碎力本質上是由主軸上的偏心激振器的離心力與動錐高速旋轉產生的慣性力提供的。由于動錐沿物料表面碾過時章動角速度很不穩定，因此無法準確計算出慣性力大小。假設物料是均勻地分布在整個破碎室的，破碎機慣性力就可以在近似無載的情況下計算出來[3]。此時破碎機的破碎力最大，如圖1所示。

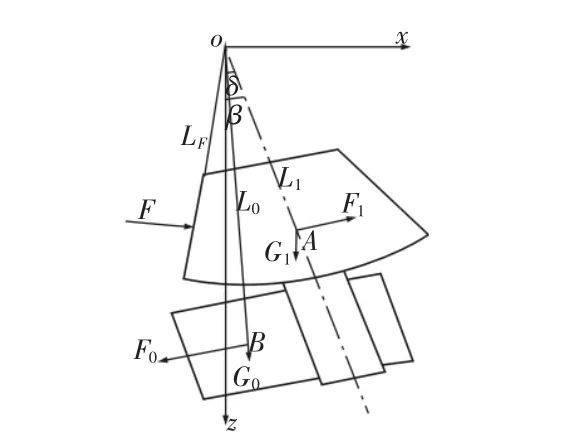
圖1 最大破碎力的計算Fig.1 Calculation of the Maximum Crushing Force

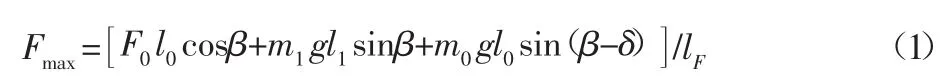
式中：F0—偏心激振器慣性力；m0—偏心塊質量；m1—動錐質量；ω—進動角速度；l1—動錐質心A點與o點連線的長度；l0—偏心塊質心B點與o點連線的長度；β—動錐中心線與定錐中心線的夾角；δ—偏心塊質心和o點連線與動錐中心線的夾角；lF—最大破碎力作用點到o點距離。

通過對o點取矩，可得最大破碎力Fmax為：

3.2 主軸受力計算

激振器對主軸作用力可用破碎力計算，如圖2所示。正常破碎力與動錐重力合成F′力，其值為：

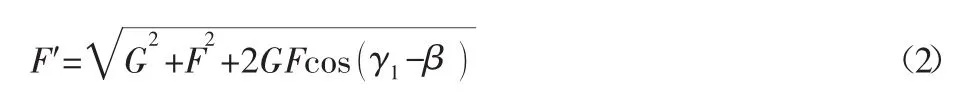
F′作用線與偏心激振器產生的慣性力的作用線交于c點，根據在同一平面內互不平行的三個力相互平衡，力作用線必匯交于一點定理，球面軸承對動錐的支持力必通過c點且該支持力的作用線通過動錐球面座中心o，根據圖2的幾何關系，可求出Fp為：

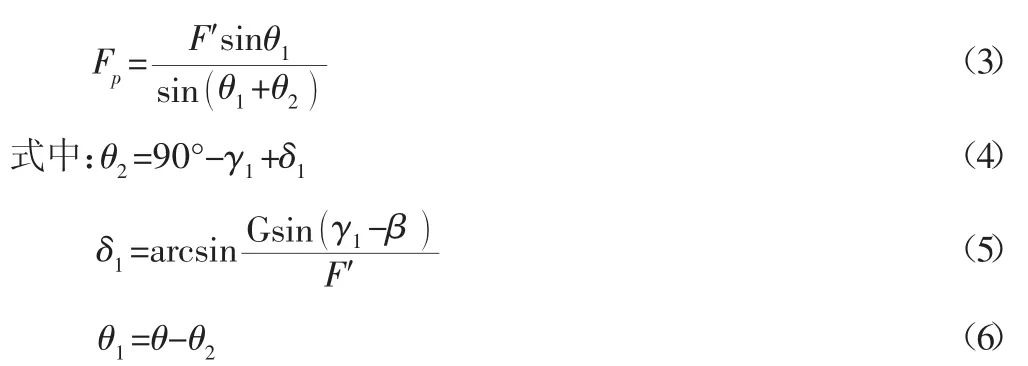
式中：Fp—正常破碎力引起的激振器對主軸作用力；Fq—球面軸承對動錐的支持力；θ1—力 F′與 Fp之間的夾角；θ2—力 F′與Fq之間的夾角；δ1—力F′與F之間的夾角；β—動錐中心線與定錐中心線夾角；γ1—動錐錐面傾角。

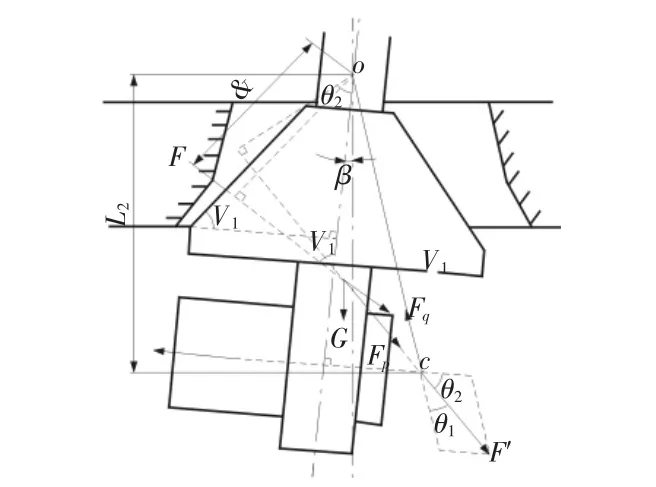
圖2 慣性圓錐破碎機主軸受力分析Fig.2 Stress Analysis of Inertia Cone Crusher Spindle

根據圖2幾何關系，可得：

由式（8）推導出式（9）為：

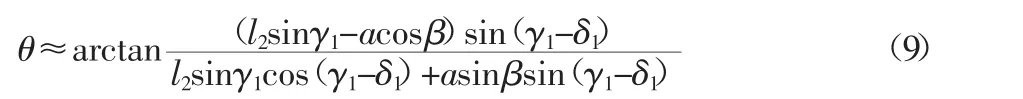
將式（4）、式（9）結果代入式（3）可求得 Fp。最大破碎力引起的激振器對主軸最大作用力Fpmax與上面求法相同可求得Fpmax=3.87×106N。

4 有限元靜強度分析

4.1 主軸有限元模型的建立

主軸材料為超高強度合金鋼42CrMo，該材料密度7.85×103kg/m3，泊松比為0.28，彈性模量為212GPa。主軸長1050mm，最小軸徑93mm，與動錐過盈配合的軸段為直徑140mm與直徑200mm軸段，各截面變化處都進行了倒角及圓角處理。該主軸結構尺寸，如圖3所示。

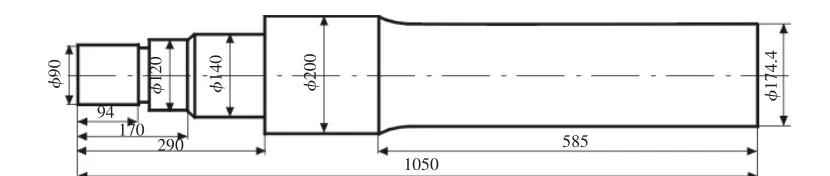
圖3 主軸結構尺寸Fig.3 Size of the Spindle

主軸劃分網格時采用由面單元通過拉伸網格產生體單元的方法建立有限元模型。首先建立關鍵點并形成軸截面，使用布爾運算利用工作坐標系將軸截面分割成若干個規則的四邊形。采用PLANE182單元利用映射網格劃分方法進行面單元網格劃分，然后通過拉伸網格生成由20節點SOLID186體單元組成的有限元模型[5]。整個模型包含122166個節點，60640個單元。

4.2 主軸約束和載荷的施加

根據慣性圓錐破碎機的實際工作情況，對主軸的上下端面進行全位移約束。主軸中部φ200圓柱面與動錐內圓錐面為過盈配合，故對此圓錐面進行全位移約束。

當偏心激振器旋轉產生離心力時，該離心力會作用在偏心激振器內圓柱面與主軸外圓柱面的切線上，由圖2可知，最大破碎力對主軸的作用力Fpmax與偏心激振器與主軸的激振力平衡，故在該切線上施加Y方向，大小為Fpmax的力[6-10]。

4.3 主軸的靜力分析結果

主軸在靜力作用下的等效應力云圖和位移云圖，如圖4、圖5所示。

由圖4可知主軸最大變形量為0.64mm，發生在偏心激振器內圓柱面與主軸外圓柱面的切線上。最小位移量為0，發生在主軸兩個端面與中部固定處。主軸變形的趨勢是向軸線凹陷。

由圖5可看出最大應力發生在激振器與底部圓柱面接觸處，最大應力為770MPa，小于材料屈服強度。另外，底部圓柱面與中部固定圓柱面結合處應力集中較大，而在實際工作中，主軸承受很大的振動沖擊載荷，此處容易發生斷軸事故，故需要適當增大過渡圓角，減小應力集中。

圖4 主軸位移云圖Fig.4 Displacement Vector Sum of the Spindle

圖5 主軸等效應力云圖Fig.5 Von Mises Stress of the Spindle

5 主軸的模態分析

在已經建立的主軸有限元模型上重新加載約束。根據主軸實際工作情況，在主軸的兩端面施加全位移約束，在動錐與主軸接觸的圓柱面施加全位移約束，采用ANSYSAPDL中的BlockLanczos法進行模態分析，并設置提取，分析主軸的前6階模態振型及固有頻率，如圖6所示。各階固有頻率計算結果，如表1所示。

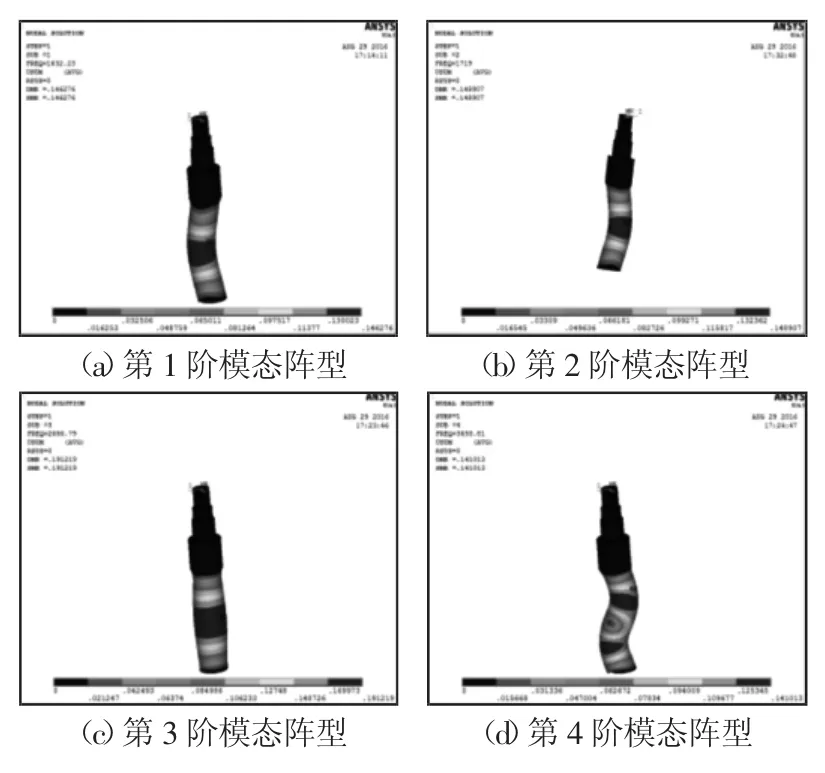
圖6 主軸前六階模態陣型圖Fig.6 The First Six Order Modal Shape of the Spindle

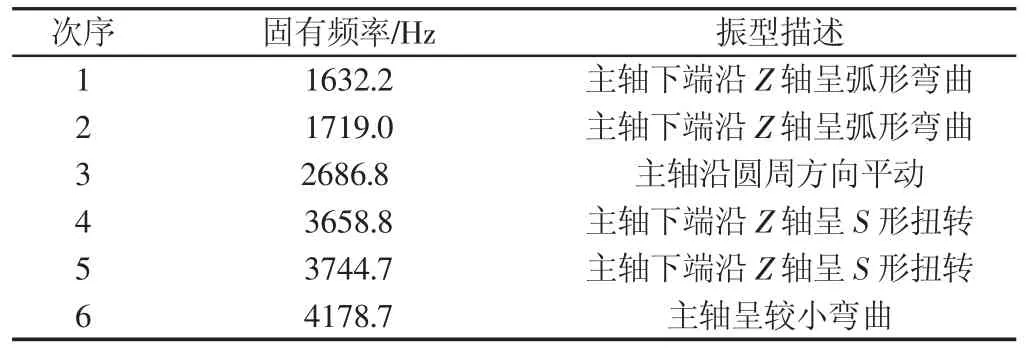
表1 前六階模態的固有頻率Tab.1 The Six Eight Order Natural Frequency of the Modality

由圖6可知，主軸主要變形部分為主軸下端與激振器接觸的內表面，主要沿z軸方向呈波浪型彎曲振動。第三階振動最劇烈，出現程度較輕的膨脹爆炸狀。第四階，第五階主軸發生扭轉變形，且變形十分明顯，設計時需要加強主軸的剛度，強度。

6 結論

對慣性圓錐破碎機主軸進行了受力分析，為主軸的受力計算提供理論依據。利用有限元軟件ANSYS APDL對主軸進行了靜強度分析與模態分析，獲得了最大破碎力下主軸的應力和變形分布規律和主軸各階的固有頻率及相應模態振型。通過計算主軸最大等效應力來校核主軸工作的安全性，通過位移云圖和等效應力云圖及固有頻率及固有振型為慣性圓錐破碎機主軸的力學分析和動力學分析提供理論依據。（1）主軸最大變形發生在偏心激振器內圓柱面與主軸外圓柱面的切線附近，最大變形量0.64mm，符合剛度要求。主最大應力發生在激振器與底部圓柱面接觸處，最大應力為770MPa，小于屈服強度930MPa，強度滿足要求。（2）慣性圓錐破碎機激振器旋轉頻率約為81Hz，遠小于主軸各階固有頻率，因此破碎機工作時不會發生公共振現象，能夠正常工作。（3）主軸是破碎機中主要的工作零件，承受破碎力很大，非常容易失效，僅對慣性圓錐破碎機主軸進行靜強度分析不夠全面，但可為后續疲勞強度分析等力學分析提供一定依據。