面向混合約束模型的線纜布線技術研究

李春泉，王弘揚，尚玉玲，周遠暢

（桂林電子科技大學 機電工程學院，廣西 桂林 541004）

1 引言

線纜作為汽車電子技術和產品的物理載體，有著至關重要的地位。隨著機電裝備日益復雜的趨勢，線纜數量和類型的增加，導致機電裝備內部空間緊張。現有的布線方法已經不能完全適應于當前環境[1]。線纜布局是一項復雜的工作，廣泛運用于許多工程領域，如機械、化工、建筑等。因為在大多數情況下，線纜布線設計是連接到工程設計的重要組成部分。在實際布線過程中，基于不同的布線約束[2]，可以以不同的方式獲得最佳的線纜路徑。因此，在線纜布局設計中，如何使布線結果是最好的（或更好）一直是一個主要的研究方向。

近年來，眾多專家學者針對布局問題進行了研究，并取得了較多的研究成果。文獻[3-4]針對空間布局問題，對基本情況進行了分析與綜述，同時提出了較好的解決方法。文獻[5]針對線纜自動布局設計問題，提出一種基于障礙物與目標吸引的改進快速隨機樹算法，能高效地完成線纜自動布線。文獻[6-7]采用三維加權網格對發動機復雜三維模型進行網格劃分，利用改進的Lee算法以及最小斯坦樹生成法，開發出航空發動機網格敷管系統。文獻[8]提出一種以線纜幾何模型信息與線束模型信息為核心，采用B樣條曲線擬合的裝配模型，對線纜布線設計過程進行仿真。由于目前線纜布線影響布局設計的約束因素過于繁雜，使得無法找到一個適用于各種約束環境的適用性方法。

因此，在相關研究工作的基礎上，建立一種布線混合約束模型，把布線問題描述為滿足一定約束的路徑搜索問題。首先，提出了約束因子、約束集合等相關概念，將布線過程中所需要的約束定義為不同的約束因子，并對不同的約束因子進行劃分，使約束功能類似約束因子組合成為相關的約束集合，每一個約束集合對應一個布線規則，使布線約束系統化。其次，將相應的布線規則進行整合，并建立布線混合約束模型。最后，對該模型進行了實例驗證。

2 線纜布局設計的約束因素分析

為了便于分析與理解布線過程中各約束，我們定義了以下基本概念。

2.1 概念的定義

定義1：約束因子CF（constraint factor）在布線過程中，對布線方案設計具有影響的因素，并在設計過程中具有一定獨立性的基本約束單元的設計變量。如線纜預留長度、最小彎角半徑、綁扎點位置、折彎半徑等。

定義2：約束集合CS（constraint set）將約束功能類似的約束因子組合形成相關的集合 CS=｛CF1，CF2，CF3，…，CFn｝。約束集合具有可擴展性和繼承性。

約束集合有子集（Sub CF）與父集（Super CF）之分，子集與父集的關系是相對的，約束集合的關系結構圖中SubCF1既是SuperCF的子集，又是SubCF11的父集，一個父集有多個子集，子集對父集具有繼承性，如圖1所示。

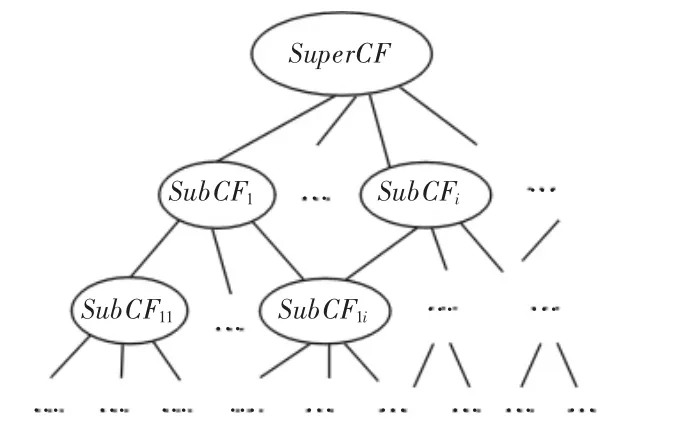
圖1 關系結構圖Fig.1 Relationship Structure Diagram

對于不同的布線布局問題，影響布局設計的約束因子是不一樣的，這使得約束的類型和數量是不確定的。通過對約束因子和約束集合的定義，對約束因子進行了分類，將具有相似約束功能的約束因子進行分類組合并建立相應的約束集合。

2.2 約束因子的基本分類

線纜布局設計應用在不同情況時雖具有一定的差異，但其約束因子的本質卻相差不大。

根據約束因子的分類原則和各約束因素的功能和屬性，將約束因子分類歸并到以下不同的基本約束集合中，如圖2所示。

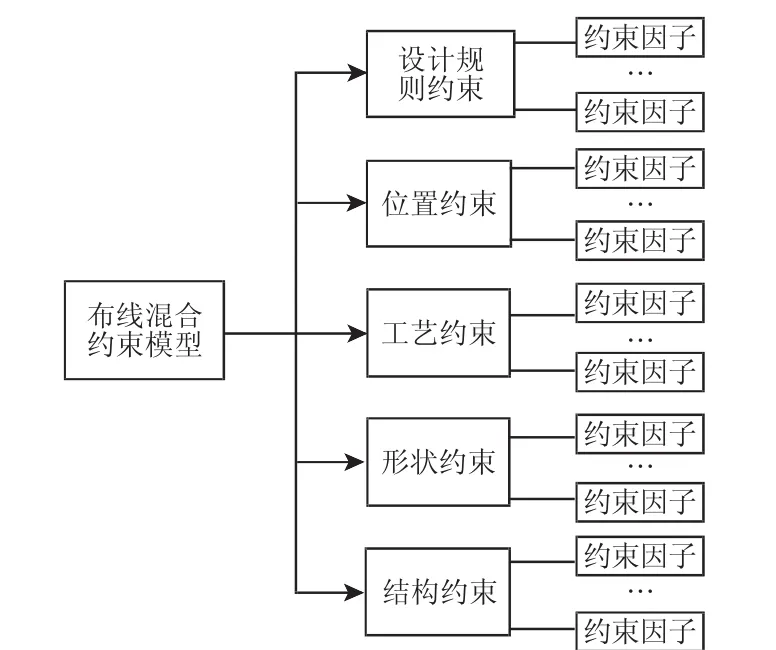
圖2 約束因子分類Fig.2 Constraint Factor Classification

2.2.1 設計規則約束集合

DCS是由與線纜機械性能有密切關系的約束因子組成的集合。一般是指在線纜布線經驗上而提出的約束。如，較長的線纜應沿車身體、結構體等支撐物布線，便于固定線纜。這是結構約束，它與線纜的機械性能有著密切關系。線纜應該盡可能多的通過已經布好的線纜的路徑，使線纜變成線束，這樣有助于節約布線空間和便于操作管理。如有頻繁操作的開關等應盡量安裝在方便的地方，或者線纜布線路徑對于維修必須是一條避開所有元件的可行路徑，這是可行約束，他與線纜維修、運行的方便程度有著密切的關系，等等。

2.2.2 位置約束集合

PCS是由與線束在實際布線過程中的位置確定有密切關系的約束因子組成的集合。一般是指結合線束在實際布線過程中的位置，線束的實際走向是根據布線過程中所涉及的諸多因素進行綜合考慮之后進行排布的。考慮到線束的低垂、移位、質量、固定方式和固定位置的方便性而提出的約束，在布線過程中必須考慮有足夠、合理的固定點和固定方式，這樣才能保證布線過程具有一定的可靠性。

2.2.3 工藝約束集合

TCS是由與線束布線工藝有密切關系的約束因子組成的集合。一般是指在實際布線過程中根據線纜的形狀、尺寸、相對位置和性質并結合線纜生產過程中的工藝過程而提出的約束。工藝約束還包括：折彎半徑、折彎最大根數、綁扎間距、綁扎點個數、預留長度等[9]。

2.2.4 形狀約束集合

FCS是由與線纜幾何形狀有密切關系的約束因子組成的集合。一般是指滿足線纜受力要求和自身材料限制的約束。其表現在很多方面，如：線纜布線時應盡量減少彎曲，避免線纜受到較大的應力。如必須彎曲時，線纜的彎角盡量≥90°，與此同時還必須滿足線纜的最小彎曲半徑。為了防止連接器發生位移從而降低了線纜的可靠性，線纜連接器接頭應采用剛性固定。在考慮到線纜的熱伸長的影響，截面積較大的線纜線芯應采用絞合分裂的線纜。線纜布線應該保證其穩定性和牢固性，避免由振動和沖擊所引發的失效和安全隱患。線纜的放置應該按照特定要求，不應出現卷曲、大量彎折等情況[10]。

2.2.5 結構約束

SCS是由與線纜結構信息有密切關系的約束因子組成的集合。一般是指滿足線纜線纜基本屬性和組成元素之間的約束。其表現在很多方面，如：根據線纜的結構信息，我們可以知道線纜任何控制點之間的連接關系，在此基礎上，將基本屬性信息和附加信息進行關聯，即可構成線纜幾何模型信息的數據來源。

通過對約束因子的基本分類之后，可以使用約束集合來定義和管理約束因子。應該指出的是，約束因子的基本分類并不意味著約束集合也隨之確定，約束集合是具有繼承性和可擴展性的，將基本的約束集合進行變換，也可派生出新的約束子集，通過變換和派生可以解決不同的布局問題。

3 基于布線混合約束模型的線纜布線算法設計

利用線纜的布線混合約束模型進行布線設計，可以使布線設計過程中所需要考慮的約束系統化，將不同約束分類應用于不同的設計場合，更能提高布線設計效率。在實際布線過程中，通常需要滿足多種復雜條件，在本實例中只針對布線混合約束模型中重點考慮的布線規則進行分析和驗證。為獲得較優的線纜敷設軌跡，將線纜的總長度作為目標函數，將布線設計中必須滿足的要求作為約束條件。其數學模型描述如下：

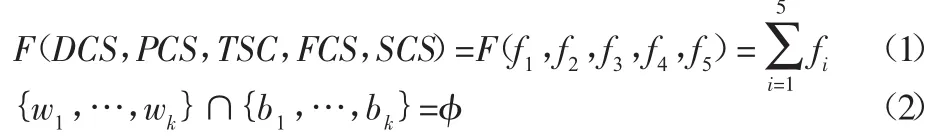
表示線纜與障礙物不能發生干涉，式中：｛w1，…，wk｝和｛b1，…，bk｝分別為線纜和障礙物的集合。

表示彎角半徑應大于線束半徑的6倍，且不得小于最大線纜半徑的10倍，式中：Bend—線束彎角半徑；D—線束半徑；d—最大線纜半徑。

表示為保證線纜的有效性，在接插件端子處給予一定的松弛量。其值不應該小于

式中：d_fixture—線纜與其它靜止機件間的最小間隙距離，為避免

線纜發生磨損及影響其性能，其值不應小于L2。

表示為保證線束容量不出現過盈現象，式中：線束容納的線纜數量不應小于規定的線束容量R，I—線束容納的線纜數量。

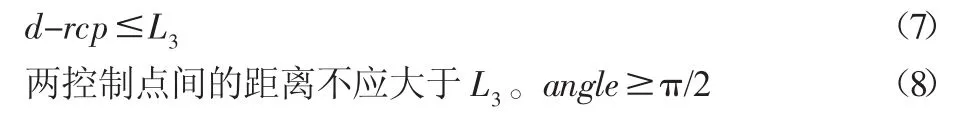
表示管路中兩段線纜的夾角，其值不小于π/2。

表示線纜起點和終點延長出的直線段，長度不小于L4。

3.1 模擬退火算法的基本思想

模擬退火算法：通過初始解i和控制參數初值t對當前解重復進行“產生新解→計算目標函數差→接受或舍棄”的迭代，并進行漸進衰減t值，根據蒙特卡羅迭代求解法的啟發式搜索過程，當算法終止時的當前解即為所得近似最優解。在算法進行時退火過程由冷卻進度表（Cooling Schedule）控制，包括控制參數的初值t及其衰減因子Δt、每個t值時的迭代次數L和停止條件S。

3.2 模擬退火算法的實現過程

Step 1：參數初始化，產生初始解 x0∈Ω，其中，Ω＝｛（x1，x2，…，xm）|xi∈｛0，1｝｝為所有可能解的集合，xi表示第 i個最優路徑點，計算相應的目標函數值W0，給出控制參數初值T0，Mapkob鏈長度N以及停止參數Tλ，設定最大迭代次數β；

Step 2：確定初始解是否可行性，若不可行，則進行調整，否則轉3；

Step 3：產生新解，判斷新解的可行性，計算新解與當前解的目標函數值差 ΔW，根據式（10）計算接受概率 P（ΔW，T），取在（0，1）上均勻分布的隨機數 θ，若 P（ΔW，T）＞θ，則接受新解，否則放棄新解。

Step 4：計算迭代次數n，若n＜N，則在此溫度下的迭代尚未結束，未完成一個Mapkob鏈長的迭代，轉步驟3；

Step 5：判斷是否滿足算法的終止準則，若迭代次數小于n最大迭代次數β且T＞Tλ繼續降溫，令T=T×α，其中α是降溫因子，繼續轉步驟3，否則，算法終止，輸出當前解。

4 應用實例

針對研究的復雜約束環境下的布線技術的內容，對某機箱部件進行線纜布線。在該實例中，采用約束條件為：L1≥2mm，L2≥10mm，L3≥50mm，L4≥70mm，angle≥π/2，D=15mm，Bend＞90mm；d=6mm，Bend＞60mm。采用MATLAB軟件進行編程和仿真，線纜端點坐標分別為 A（2，12），B（12，2）。在滿足約束模型的情況下，分別采用模擬退火（Simulated Annealing）算法、蝙蝠算法（Bat Algorithm）、粒子群（ParticleSwarmOptomization）算法進行計算仿真，完成了布線，并將仿真結果進行對比，驗證了該約束模型計算的可行性。運行50次且最大迭代次數為200，將模擬退火算法（SA）、蝙蝠算法（BA）、粒子群算法（PSO）運算結果進行對比，如表1所示。

表1 參數意義說明Tab.1 Parameter Meaning Description

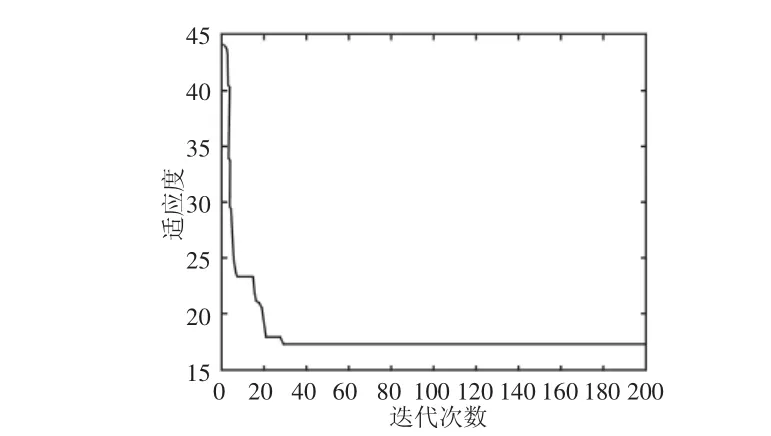
圖3 收斂曲線Fig．3 Convergence Curve

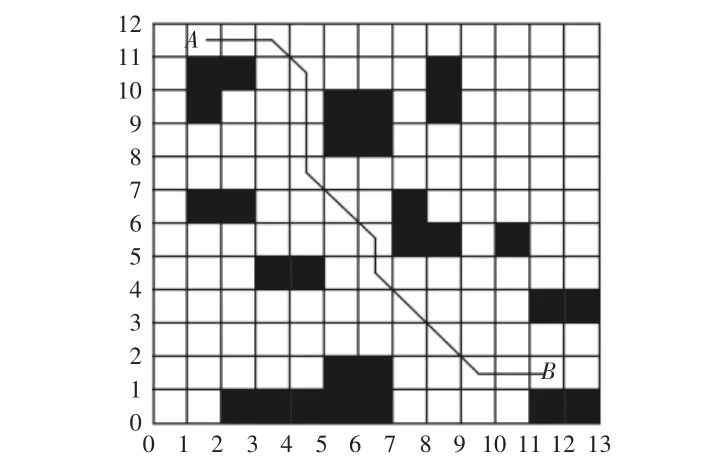
圖4 線纜布線圖Fig．4 Cable Wiring Diagram

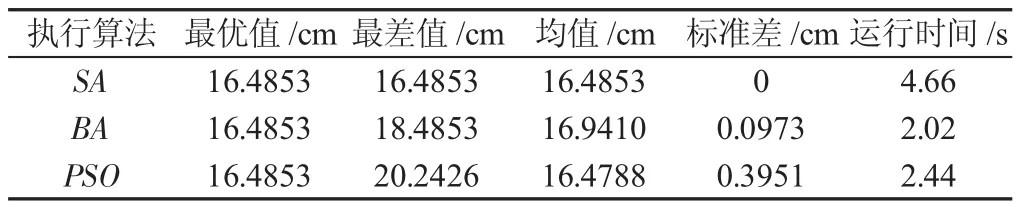
表2 算法對比Tab.2 Algorithm Comparison

由表1可知，模擬退火算法（SA）運算結果穩定，標準差為0，尋優率最高。

5 結論

針對線纜布線方法問題，提出了一種基于布線混合約束模型的布線方法。結論如下：（1）該方法有效的滿足了一系列約束，并能夠實現基于布線混合約束模型的走線方式。（2）根據約束因子、約束集合等概念有效的解決了在錯綜復雜的布線環境中，運用布線混合約束模型，生成了路徑，取得了較好的布線成果。（3）通過實驗，將模擬退火算法（SA）、蝙蝠算法（BA）、粒子群算法（PSO）運算結果進行對比，驗證了該方法的有效性。