城市電動物流車EPS系統模糊PID控制策略研究

孟令廣，牛志剛

（太原理工大學 機械工程學院，山西 太原 030024）

1 引言

汽車作為人們生活中最常用的交通工具，其數量正不斷增加，汽車所消耗的能源和排放的廢氣也不斷增加，這種趨勢與當今社會的節能、環保兩大主題相背離[1]。因此，許多國家都開始研究新能源汽車。

助力轉向系統是現代汽車結構中必不可少的一部分，傳統液壓助力轉向系統存在結構復雜、效率低、易泄露等弊端；而電動助力轉向系統只依靠電動機提供轉向助力，具有機構簡單、控制靈活、效率高等諸多優點[2]。并且助力電機只是在有轉向操作時才轉動，與液壓助力相比可以顯著降低能耗[3]；此外，還可以提供合理的助力轉矩來適應不同的車速，更好地協調了駕駛輕便性和路感[4]。

控制方式的選擇是EPS（ElectricPowerSteering，簡稱EPS）系統的重要部分，尤其是控制規律的選擇[5]。傳統的PID控制策略由于在參數設置上的固定性導致助力轉向系統對于外界條件改變下的適應能力變差，而且不具有在存在干擾條件下自我調整的功能。模糊控制由于其獨特的計算原則，對于沒有準確數學模型控制系統具有較強的適應性與自我調整性；模糊PID控制策略在結合上述兩種控制方法的基礎上，充分發揮了PID控制策略消除穩態誤差的特點，又很好地避免了控制對象數學模型不確定情況下產生的參數不固定的情況，發揮了模糊控制的優勢[6-7]。在設定好的模糊控制規則的自我調整下，不需要推導出EPS助力轉向系統的準確數學模型就可以對非線性的轉向系統進行良好的控制[8]。

2 EPS系統的結構及工作原理

電動助力轉向系統的組成結構，如圖1所示。轉向器選擇齒輪齒條式，助力方式為轉向軸助力式，方向盤轉矩通過扭矩傳感器來測得。當駕駛員有轉向操作時，扭矩傳感器發出一個電壓信號，電子控制單元（ECU）根據電壓信號值計算出方向盤轉矩的大小和方向；同時，車速傳感器將檢測到的當前車速傳遞到ECU。ECU先根據車速選擇與之對應的助力特性曲線，再根據方向盤轉矩計算出目標助力轉矩的方向和大小，最后確定助力電機的旋轉方向和驅動電流的大小，助力電機根據得到的驅動電流提供相應的助力轉矩，經減速器減速增扭后施加到轉向機構，為轉向系統提供與工況相適應的助力[9]。

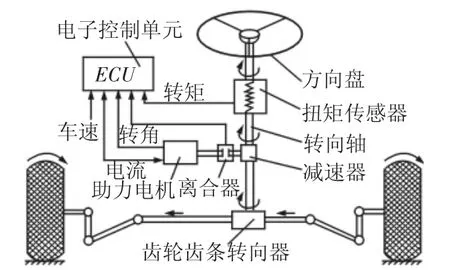
圖1 電動助力轉向系統機構簡圖Fig．1 Diagram of EPS

3 助力特性曲線選擇

汽車的行駛環境比較復雜，在不同的行駛工況轉向時，轉向系統根據當前車速選擇適合的助力特性曲線，再根據方向盤轉矩和選擇的助力特性曲線計算出需要提供的助力轉矩的大小，從而保證汽車在低速轉向行駛時的輕便靈活性和高速轉向時的路感。

現如今普遍采用的助力特性曲線有：直線型、折線型和曲線型。這三種曲線中，直線型最簡單，數據量小，便于存儲，降低了控制系統的設計要求，并且方便調整，適合用在前軸負荷較小的汽車上[4]；曲線型最復雜，能夠實現連續均勻地提供助力，但數據存儲量大，調整起來比較繁瑣，適合用在前軸負荷較大的汽車上；折線型的助力特性介于兩者之間。試驗中改裝的是一款城市物流車，其電子控制技術和智能化水平都不是很高，運行工況相對良好，為了在保證助力需求的基礎上盡可能的降低成本，故選用直線型助力特性曲線。

EPS系統在不同車速所對應的助力曲線參數，如圖2所示。實驗車的最高車速約為100km/h，x軸是駕駛員作用在方向盤上面的力矩，范圍在（0～8）N·m，y軸是助力電機作用在轉向軸上面的助力轉矩，最大為14．8N·m，在車速為0km/h時取得。圖中可以看出車速較低時，助力特性曲線的增益系數相對比較大，使低速轉向時更加輕便靈活；車速較高時，助力特性曲線的增益系數比較小，保證了高速轉向時駕駛員的路感。

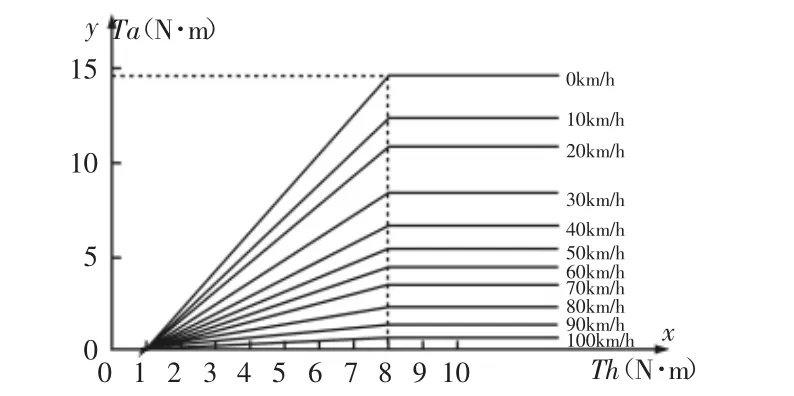
圖2 理想電動助力轉向模型Fig．2 The Ideal Model of Electric Power Steering

4 EPS系統數學模型的建立

建立動力學模型時，為減小仿真模型與真實情況的誤差添加相應阻尼、剛度系數等。

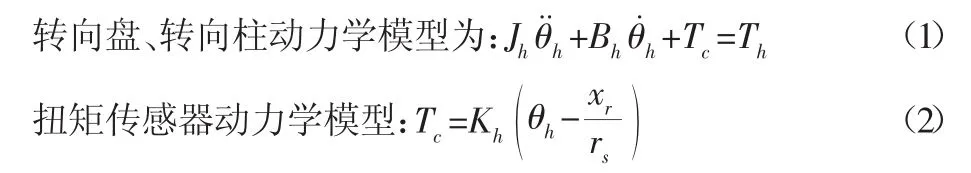
助力電動機動力學模型[10]：

式中：Th、Ta、Tc、Tm—方向盤轉矩、電機助力轉矩、扭矩測量轉矩、助力電機輸出轉矩；θh、θm—方向盤轉角、助力電機轉角；Jh、Jm—方向盤和助力電機的轉動慣量；Kh、Km、Ka、Kb—轉向柱剛度系數、助力電機剛度系數、助力電機電磁轉矩系數、助力電機反電動勢常數；xr—轉向橫拉桿位移；rs—轉向小齒輪分度圓半徑；U、R、L、I—助力電機的電壓、電阻、電感、電流；Bh、Bm、Br—轉向柱阻尼系數、助力電機阻尼系數、轉向橫拉桿阻尼系數；G—減速機構傳動比；Mr—轉向橫拉桿質量；FTR—轉向負荷。

5 EPS系統模糊PID控制器設計

控制器設置兩個輸入量和三個輸出量，以計算得到的理想電流與實際檢測到的電流的誤差e和誤差變化率ec作為輸入，經過模糊PID控制器的運算得到控制系統的精確參數，進而控制電動汽車的助力轉向執行器，使汽車轉向模型按照理想的助力轉向特性進行轉向。

以模糊PID作為控制策略的EPS系統流程圖，如圖3所示。先將精確的輸入量電流誤差e和誤差變化率ec轉化為模糊的語言變量E和EC，然后根據模糊規則進行模糊推理得到輸出值的語言變量ΔKP、ΔKI和ΔKD，再將語言變量、和解模糊化得到精確的輸出值Δkp、Δki和Δkd，實現控制參數的實時控制。

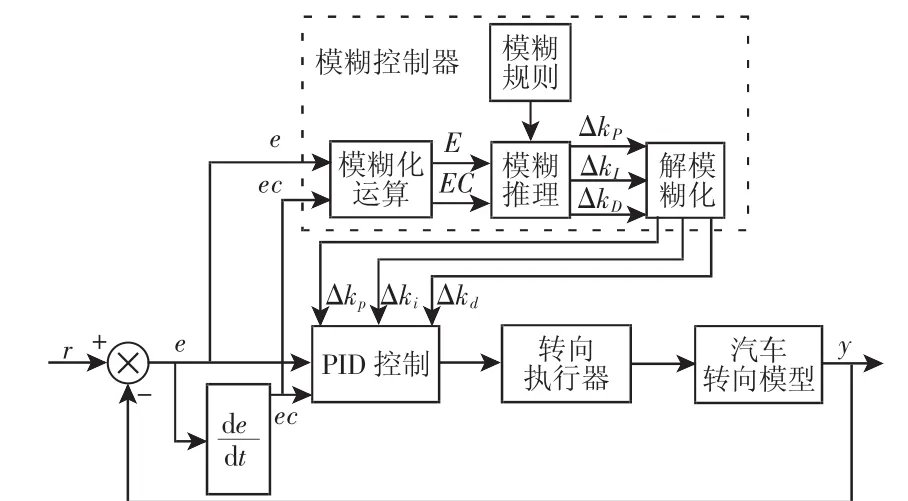
圖3 基于模糊PID控制的EPS系統Fig．3 Fuzzy PID Control for EPS System

5.1 模糊語言設計

模糊控制器的語言變量有5個：電流誤差e、誤差變化率ec和PID三個參數的修正值。其中電流誤差e和誤差變化率ec為輸入變量，Δkp、Δki和Δkd為輸出變量。電流誤差e和誤差變化率ec的基本論域分別為［-15，15］，［-7，7］；在線調整 3 個輸出變量Δkp、Δki和 Δkd的基本論域分別為［-2，2］，［-0．6，0．6］，［-0．02，0．02］。變量 e、ec、Δkp、Δki和 Δkd都采用 7個模糊子集描述，即｛NB、NM、NS、ZE、PS、PM、PB｝。

5.2 模糊控制規則

為了實現在線調整PID控制參數的目的，根據不同的電流誤差e和誤差變化率ec，Δkp、Δki和Δkd的控制規則，如表1～表3所示。

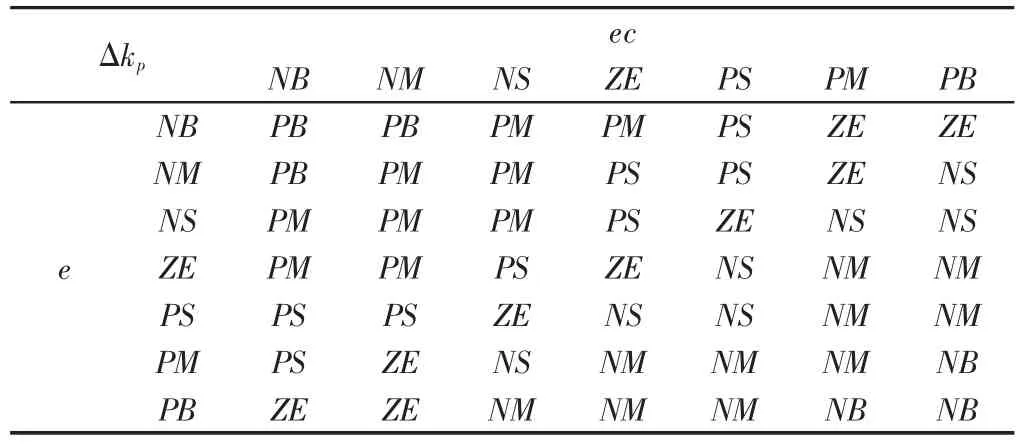
表1 Δkp模糊控制規則表Tab.1 ΔkpFuzzy Control Rule Table

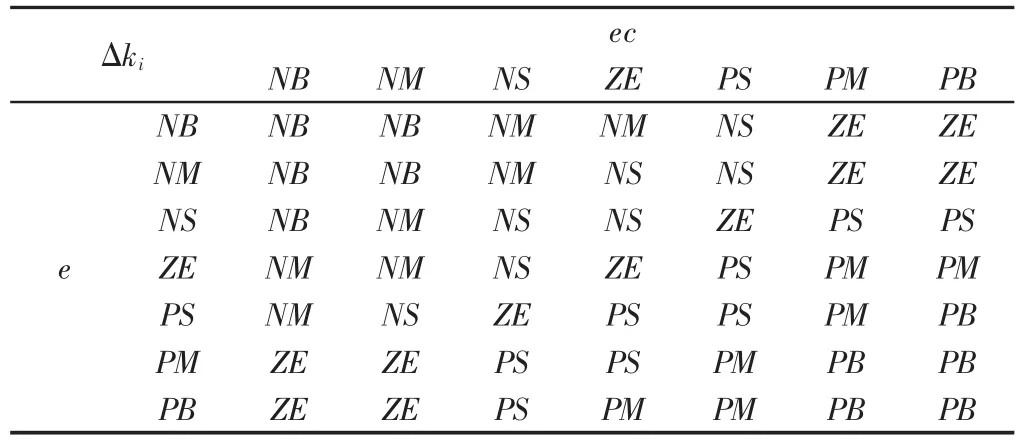
表2 Δki模糊控制規則表Tab.2 ΔkiFuzzy Control Rule Table

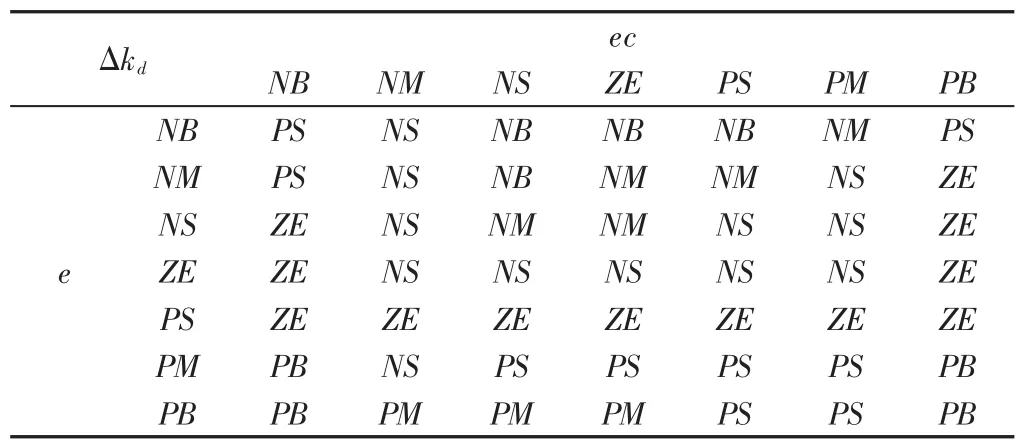
表3 Δkd模糊控制規則表Tab.3 ΔkdFuzzy Control Rule Table

6 EPS系統仿真分析

6.1 仿真模型

實驗用車在MATLAB/Simulink中搭建的系統模型，如圖4所示。汽車EPS系統的整體控制模型，如圖4（a）所示。封裝的模糊PID控制器運算系統，如圖4（b）所示。模糊控制器首先將精確的車速和轉矩參數做模糊化運算，再對照模糊規則執行模糊推理，最后對輸出結果的模糊變量解模糊化處理，從而得到比例、積分和微分系數的最后調整值Δkp、Δki、Δkd，代入下式計算：

式中：kp0、ki0、kd0—參數設置的初值；kp、ki、kd—最后調整結果。

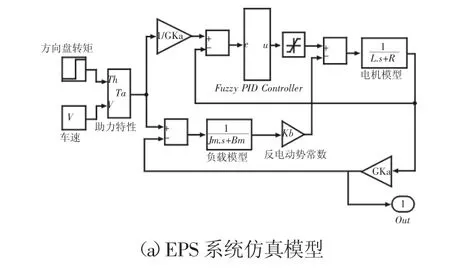
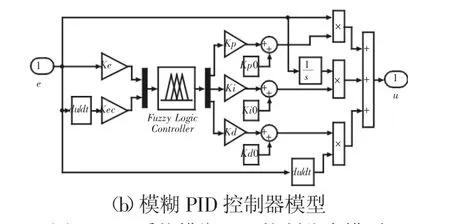
圖4 EPS系統模糊PID控制仿真模型Fig.4 Fuzzy PID Control Simulation Model for EPS System

6.2 仿真結果分析

以階躍信號為輸入，助力轉矩為輸出，對EPS系統模型進行仿真。不同車速下PID與模糊PID仿真結果對比，如圖5所示。

其中，圖5（a）為當V=20km/h時，助力特性曲線的增益系數為1.55，如果此時方向盤輸入4N/m的轉矩，則助力轉矩應為6.2 N·m。當系統采用傳統PID調節時，調整時間為0.41s，超調量為16%；當采用模糊PID控制策略時，系統調整時間降低為0.2s，超調量為8.8%，模糊PID的控制性能明顯優于PID控制。

圖5（b）又對車速分別在V=40km/h和V=60km/h時系統的響應特性進行了仿真，車速在V=40km/h時，傳統PID調整時間為0.42s，超調量為17.4%；模糊PID控制策略調整時間為0.2s，超調量為8.6%。車速在V=60km/h時，傳統PID調整時間為0.41s，超調量為16.9%；模糊PID控制調整時間為0.19s，超調量為8.6%。結果表明采用模糊PID控制策略的EPS系統助力特性具有超調量小、調整時間短的特點，可以很好地滿足不同車速的助力轉向需要。

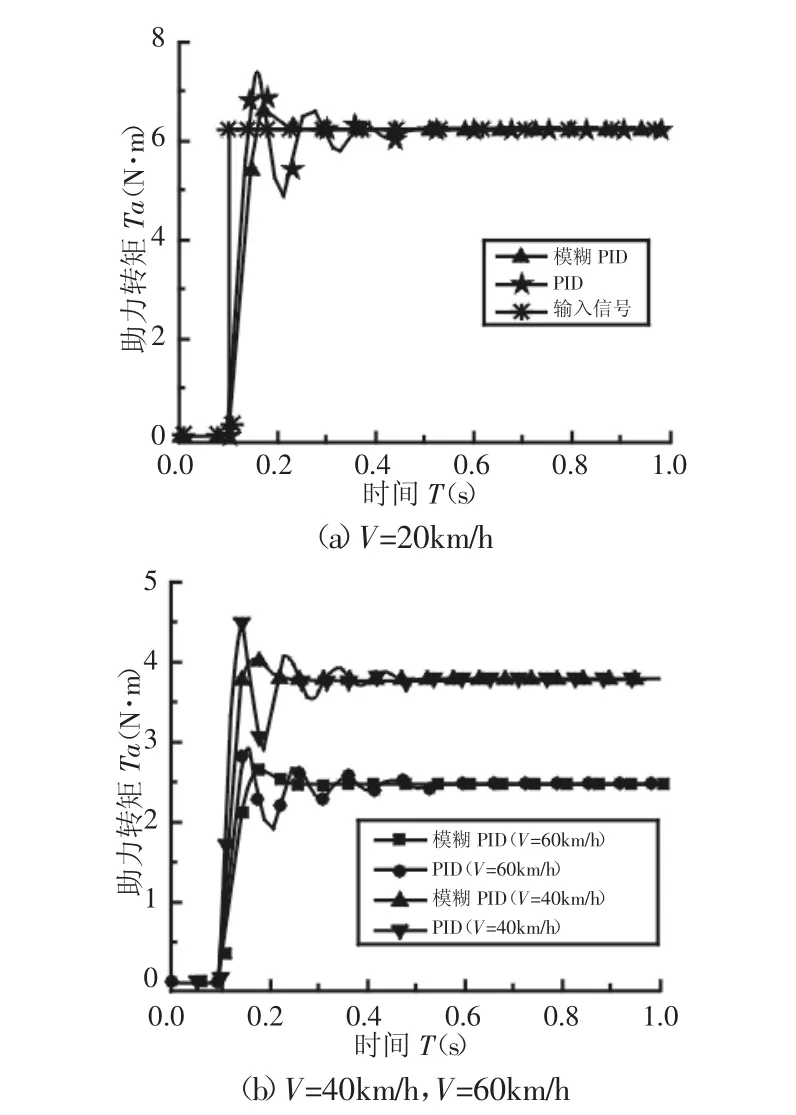
圖5 不同車速PID與模糊PID仿真結果對比Fig.5 The Contrast of PID and Fuzzy PID Simulation Results in Different Speed

汽車在實際運行過程中，由于路況等因素的改變，會對轉向系統產生一定干擾，針對這一現象，在仿真中加入干擾信號驗證模糊PID的抗干擾能力，結果，如圖6所示。在0.7s時，施加26%的干擾信號，模糊PID在0.12s的調整后重新達到穩定；而PID則需要0.25s的調整時間，由此可見，模糊PID控制策略的抗干擾能力也優于PID。

圖6 有干擾時PID與模糊PID仿真結果對比Fig.6 The Contrast of PID and Fuzzy PID Simulation Results with Interference

7 結論

以EPS系統為控制對象，借助模糊PID控制策略解決了被控對象沒有精確數學模型的問題，運用Simulink進行仿真，獲取了EPS系統的控制參數。（1）在相同輸入信號下，模糊PID較傳統PID超調量減少，調整時間減少，優化了EPS系統的助力特性。（2）汽車在不同車速轉向時，模糊PID均能快速平穩的提供助力轉矩，很好地滿足轉向需求。（3）汽車在許多復雜的工況行駛，采用模糊PID控制策略可使系統對外界的干擾及時進行調整，從而提高EPS系統的抗干擾能力。