隨機(jī)矩陣研究

劉 艷

（呂梁學(xué)院汾陽師范分校，山西汾陽032200）

1 預(yù)備知識

隨機(jī)矩陣作為非負(fù)矩陣的一種，適用于非負(fù)矩陣的各種概念和結(jié)果。為了更容易理解隨機(jī)矩陣，我們首先介紹非負(fù)矩陣的有關(guān)概念和性質(zhì)。

定義1[1]設(shè)A=(aij),B=(bij)∈Rm×n，如果對所有的i,j都有aij≥bij，則記為A≥B。如果對所有的i,j都有aij＞bij，則記為A＞B，特別的，如果A≥0，則稱A為非負(fù)矩陣。如果A＞0，則稱A為正矩陣。

我們用||A表示任意矩陣A=(aij)∈Cm×n的元素取模之后得到的非負(fù)矩陣，即 ||A=(||aij)；特別的，當(dāng)x=(x1,x2,…,xn)T∈Cn時，||x=(||x1, ||x2,…, ||xn)T。

考慮n個隨機(jī)事件組S1,S2,…,Sn及時間序列t0,t1,t2,…,tn，如果在這些時刻的每一瞬間，這事件組有且只有一個能夠出現(xiàn)，如果在時刻tk-1出現(xiàn)的事件為Si，則Si在時刻tk出現(xiàn)的概率記為pij(i,j=1,2,…,n;k=1,2,…)。又假設(shè)條件概率pij(i,j=1,2,…,n)與下標(biāo)數(shù)k無關(guān)。

當(dāng)給出了有限事件的純馬爾科夫（Markov）鏈時，也就說給出了條件概率矩陣P=(pij)n×n。對條件概率矩陣P=(pij)n×n，顯然有

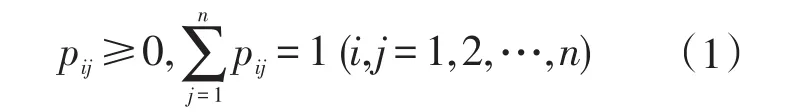
引理1[2]若A為隨機(jī)矩陣，則其對應(yīng)于特征值1的Jordan塊均為一階的。

引理2[1]n階非負(fù)陣A為不可約的充分必要條件是(E+A)n-1＞0。

2 隨機(jī)矩陣的定義及有關(guān)結(jié)論

定義2[3]非負(fù)矩陣A=(aij)n×n稱為一個隨機(jī)矩陣，如果A的每一行上的元素之和都等于1，從隨機(jī)矩陣的定義可知，隨機(jī)矩陣A有特征值1，并且與之對應(yīng)的有正特征向量Z=(1,1,…,1)T。反之，若每個非負(fù)的n階矩陣A有特征值1，并且對應(yīng)于1的特征向量為(1,1,…,1)T時，則A都是隨機(jī)矩陣。

定理1非負(fù)矩陣A=(aij)n×n為隨機(jī)矩陣的充分必要條件是矩陣A有特征值1，并且n維向量Z=(1,1,…,1)T是與1相應(yīng)的一個正的特征向量。

容易看出，隨機(jī)矩陣A的其他特征值的模都不超過1。因此，特征值1就成為了隨機(jī)矩陣A的極大特征值[4]。

下面介紹一種特殊的非負(fù)矩陣，即具有正極大特征值與對應(yīng)正特征向量的非負(fù)矩陣，它與定義2中的隨機(jī)矩陣具有密切關(guān)系。

定理2若非負(fù)矩陣A=(aij)n×n有正的極大特征值r=ρ(A)＞0，并且對應(yīng)于特征值r有正的特征向量Z=(z1,z2,…,zn)T＞0，則矩陣A能相似于數(shù)r與某個隨機(jī)矩陣P的乘積

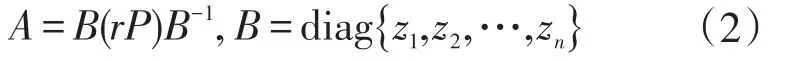
也即，(B-1AB)∕r為隨機(jī)矩陣。

證由于

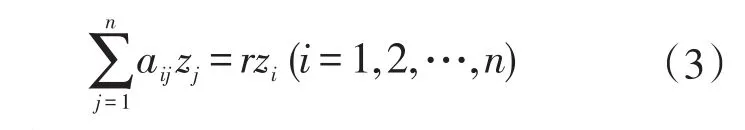
定義對角矩陣

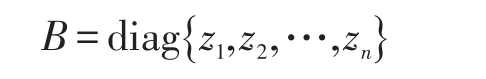
及矩陣

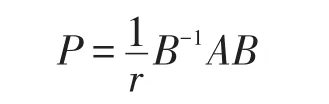
因而

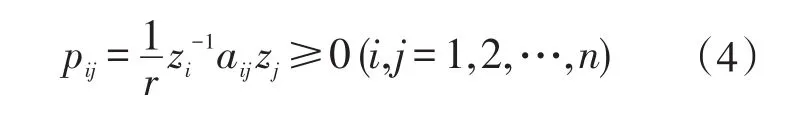
再結(jié)合式（3）可得

因此，P為隨機(jī)矩陣，并且有A=B(rP)B-1，證畢。

3 隨機(jī)矩陣A的冪序列{Am}的收斂性

在實際應(yīng)用中，常常需要考慮隨機(jī)矩陣A的冪序列{Am}的收斂性。

定理3設(shè)A為n階隨機(jī)矩陣，則A的冪序列{Am}收斂的充分必要條件是A的不等于1的特征值的模均小于1。

證明由引理1，A的對應(yīng)于特征值1的Jordan塊均為一階的.于是存在可逆陣P使得

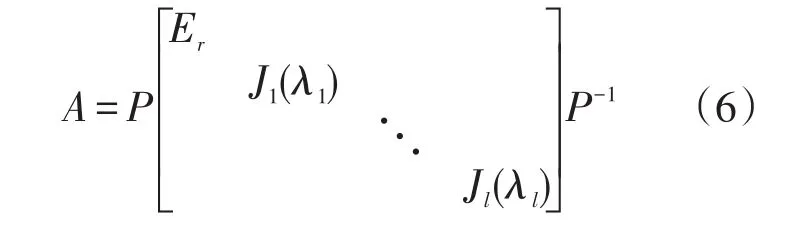
其中，Ji(λi)是Jordan塊；λi≠1, ||λi＜1,i=1,2,…,l，則對于任意正整數(shù)m，有

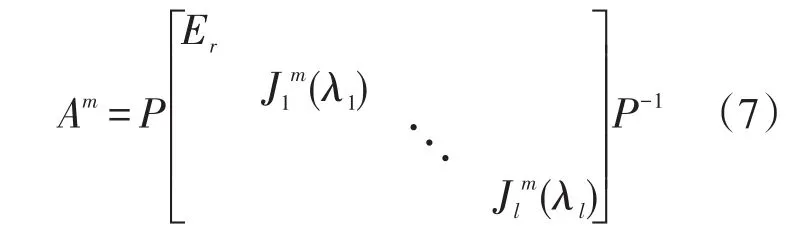
由式（7）可知，A的冪序列{Am}收斂的充分必要條件是λi≠1,|λi|＜1,i=1,2,…,l。證畢。

下面通過實例說明定理3的應(yīng)用。

例考慮3個高校間的人才流動問題。設(shè)甲、乙、丙3個高校各有專業(yè)人才分別為200人，600人，1 000人，教育行政主管部門要求每年每個單位把所有人才各分一半與其他兩個單位交流。問明年、后年3個高校的人才分布情況如何？多年后各單位的人才期望值是多少?

解我們用分別表示第k年甲，乙，丙3個單位的人才數(shù)，則表示一個具有三個狀態(tài)的齊次Markov鏈，它的轉(zhuǎn)移矩陣和初始分布向量分別為

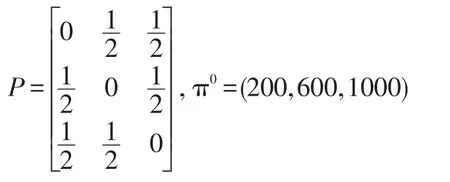
并且πk滿足

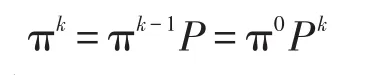
于是

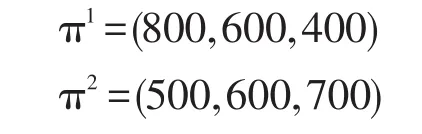
由于P的特征值為，從而由定理3可知，lki→m∞Pk存在。事實上

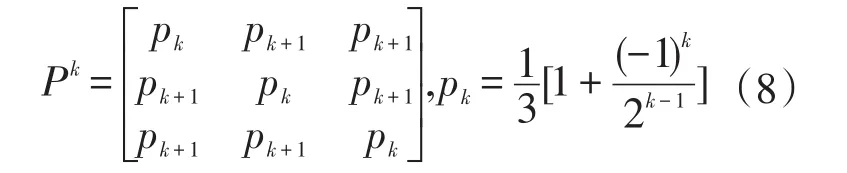
令k→∞，對式（8）兩邊取極限可得

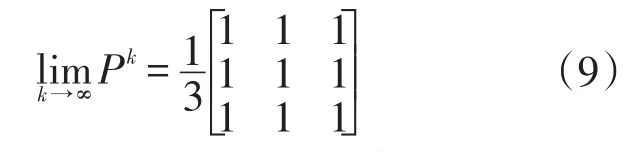
式（9）即說明多年后，甲、乙、丙3個單位的人才數(shù)為一穩(wěn)態(tài)的分布向量

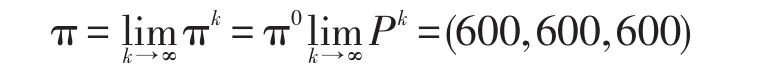
此外，由于E+P＞0從而(E+P)2＞0，由引理2可知，P是不可約的非負(fù)矩陣。