關于Fermat型函數(shù)方程的亞純解

段江梅

（昭通學院數(shù)學與統(tǒng)計學院，云南昭通 657000）

1 引言及主要結果

1637年法國數(shù)學家費馬提出了如下猜想：當n≥3時，丟番圖方程xn+yn=zn沒有非平凡的整數(shù)解。1994年這個猜想被英國數(shù)學家A.Wiles完全證明。要尋找方程xn+yn=zn在整數(shù)環(huán)上的非平凡解，可以轉化為求代數(shù)曲線xn+yn=1上的有理點。

然而早在1965年，當n≥2時，關于Fermat型函數(shù)方程

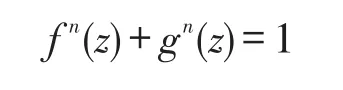
在整函數(shù)環(huán)，或是亞純函數(shù)域上的非平凡解的狀況已經完全清楚了。

類似地，研究丟番圖方程xn+yn+zn=tn整數(shù)解的存在性問題可以轉化為研究方程xn+yn+zn=1的有理數(shù)解的存在性問題。然而，當n≥6時，方程xn+yn+zn=tn整數(shù)解的狀況不是十分清楚。

相應地，不妨先考慮當n≥2時，F(xiàn)ermat型函數(shù)方程

在整函數(shù)環(huán)，或是亞純函數(shù)域上的非平凡解。對于該問題的研究已有如下結論：

1985年 W.K.Hayman〔1〕證明了：當n≥9時，方程（1）不存在非常數(shù)亞純解；當n≥7時，方程（1）不存在非常數(shù)整函數(shù)解。

此外，當 2≤n≤5時，G.G.Gundersen等〔2-4〕找到了滿足方程（1）的非常數(shù)整函數(shù)解；當n=6時，G.G.Gundersen〔5〕構造了滿足方程（1）的非常數(shù)亞純解。

近期，蘇敏等〔6〕證明了：當n=6時，方程（1）不存在級小于1的非常數(shù)整函數(shù)解；當n=8時，方程（1）不存在級小于1的非常數(shù)亞純函數(shù)解。

本文對n=7時函數(shù)方程（1）亞純解的存在性問題進行了探究，得到以下結論：

定理1 設f(z)，g(z)及h(z)均為非常數(shù)亞純函數(shù)，它們滿足：

（i）f7(z)+g7(z)+h7(z)=1；

（ii）f(z),g(z),h(z)無公共單重極點，則τ(z)是整函數(shù)，其中

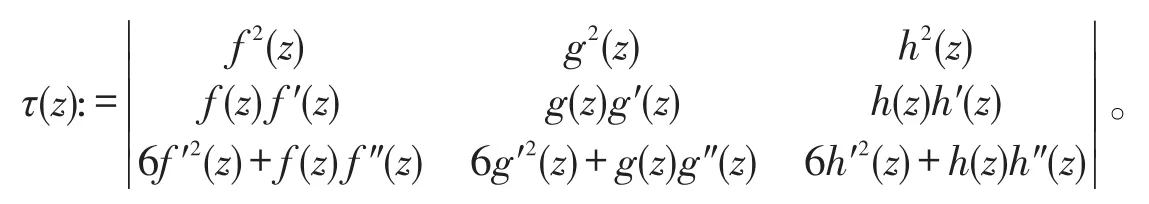
定理2 函數(shù)方程

無滿足如下條件的非常數(shù)亞純解：

（i）f(z),g(z),h(z)至多有一個公共單重極點；

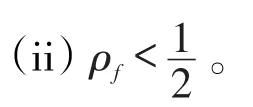
2 幾個引理

在定理的證明之前，先介紹本文中常用的幾個引理。

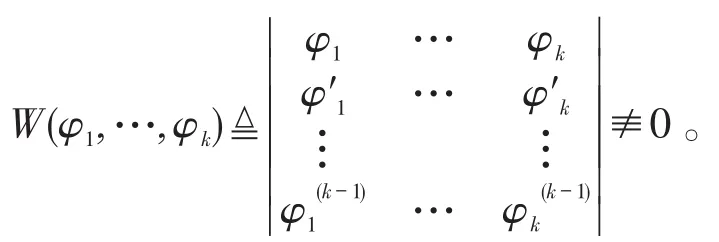
引理1 若(j=1,2,…,k)為區(qū)域D內k個亞純函數(shù)，且的Wronskian行列式〔7〕線性無關，那么φ1,…,φk

引理2 若f(z)是C上的亞純函數(shù)，那么對?k∈N，f(k)(z)與f(z)的級相同〔8〕。

引理3 若是非常數(shù)亞純函數(shù)，且，那么〔9〕

特別地，若非常數(shù)亞純函數(shù)g(z)的級ρg＜1，則有

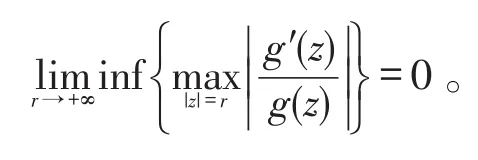
3 定理的證明

3.1 定理1的證明 由于f(z),g(z),h(z)為方程f7(z)+g7(z)+h7(z)=1的非常數(shù)亞純解，則f7(z),g7(z),h7(z)一定線性無關，從而W(f7(z),g7(z),h7(z))?0。

由（2）可得方程組

則

從而τ(z)?0。

由克萊姆法則得

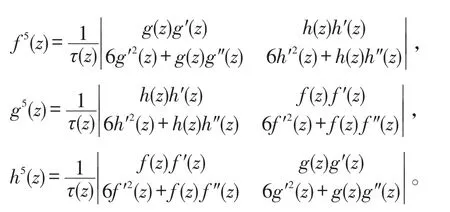
于是

同理可得：

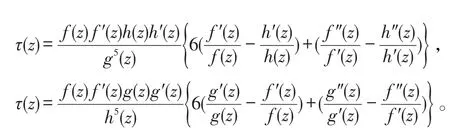
我們斷言：當f(z),g(z)及h(z)無公共單重極點時，τ(z)為整函數(shù)。

事實上，若τ(z)有極點，只可能在f(z)或g(z)或h(z)的極點處產生。用p,q,t分別表示f(z),g(z),h(z)以z0為極點的重數(shù)。由方程（2）知，若z0是f(z),g(z),h(z)中任意一者的極點且重數(shù)為max{p,q,t}，那么z0至少也為其余兩個（亞純函數(shù)）中一者的極點，且重數(shù)也為max{p,q,t}，由f(z),g(z),h(z)的對稱性，不妨設 max{p,q,t}=p=q，則p=q≥t。在z0的某去心鄰域內，設

其中為解析部分。

下面分3種情況討論：

1）若p=q=t≥2，則

注意到p≥2，所以τ(z)在z0處解析。

2）若p=q＞t≥1（當t=1時，p≥2），則

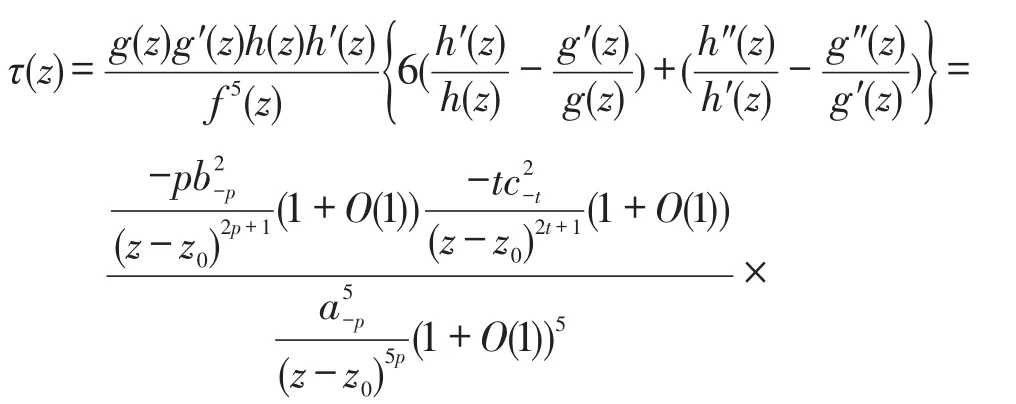
注意到p＞t≥1（當t=1時，p≥2），因此τ(z)在z0處解析。

3）若p=q＞t=0 ，顯然τ(z)在z0處解析。

因此，斷言成立。

3.2 定理2的證明 假設方程（2）存在滿足條件的亞純解f(z),g(z),h(z)，

令

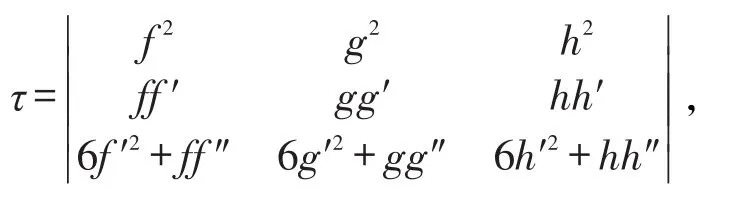
則由定理1的證明過程知：

且

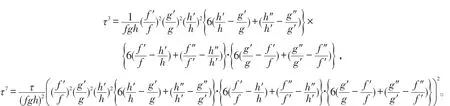
下面分兩種情形證明：

情形1 當f(z),g(z)及h(z)沒有公共單重極點時，由定理1知：τ為整函數(shù)。

又由引理2和方程（2）知

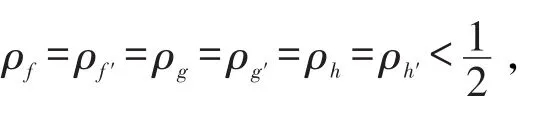
故由引理3得

又因為τ是整函數(shù)，故τ=0，與（3）式矛盾。

情形2 當f(z),g(z)及h(z)的公共單級極點有且僅有一個，設為z0，在z0的某去心鄰域內，設

令F(z)=f((z-z0)2+z0),G(z)=g((z-z0)2+z0),H(z)=h((z-z0)2+z0)，則z0為F(z),G(z),H(z)的公共二重極點，且F7(z)+G7(z)+H7(z)=1。

令

則τ～≡ 0，且τ～在z0處解析。

又由于ρF=2ρf＜1，故由引理3知，τ～=0 ，矛盾。

綜上，結論得證。

〔1〕HAYMAN W K. Warings Problem für analytische Funktionen〔J〕. Bayerische Akademie der Wissenschaften Ma-thematisch-Naturwissenschaftliche Klasse，1985，1984：1-13.

〔2〕MOLLUZZO J.Monotonicity of Quadrature Formulas and Polynomial Representation〔J〕.Doctoral Thesis，1972.

〔3〕GREEN M.Some Picard Theorems for Holomorphic Maps to Algebraic Varieties〔J〕.American Journal of Mathematics，1975，97（1）：43-75.

〔4〕GUNDERSEN G G，KAUYA T.Entire and Meromorphic Solutions off5（z）+g5（z）+h5（z）=1〔J〕.In Symposium on Complex Differential and Functional Equations，2004（1）：57-67.

〔5〕GUNDERSEN G G.Meromorphic Solutions off6（z）+g6（z）+h6（z）=1〔J〕.Analysis，1998（18）：285-290.

〔6〕蘇敏，李玉華.關于函數(shù)方程非平凡亞純解的研究〔J〕.云南師范大學學報（自然科學版），2009，29（2）：41-44.

〔7〕顧永興，龐學誠，方明亮.正規(guī)族理論及其應用〔M〕.北京：科學出版社，2007.

〔8〕楊樂.值分布理論及其新研究〔M〕.北京：科學出版社，1982.

〔9〕LI Y H.Uniqueness theorems for meromorphic functions of order less than one〔J〕.Northeast Math J，2000，16（4）：411-416.