基于改進型誤差函數的復值BP神經網絡對股票價格的預測研究

馬 健，盛 魁，董 輝

(亳州職業技術學院信息工程系，安徽亳州 236800)

近年來，金融投資越來越受到人們的關注。在眾多的理財投資當中，選擇股票的投資人群所占比例較大，從過去的上證到深證以及現在的滬港通，吸引了很多股票投資者[1]。股票市場是一個波動頻繁、風險較大的市場，存在著很多不定因素，是一個非線性的復雜系統。因此，股票走勢很難精準預測。

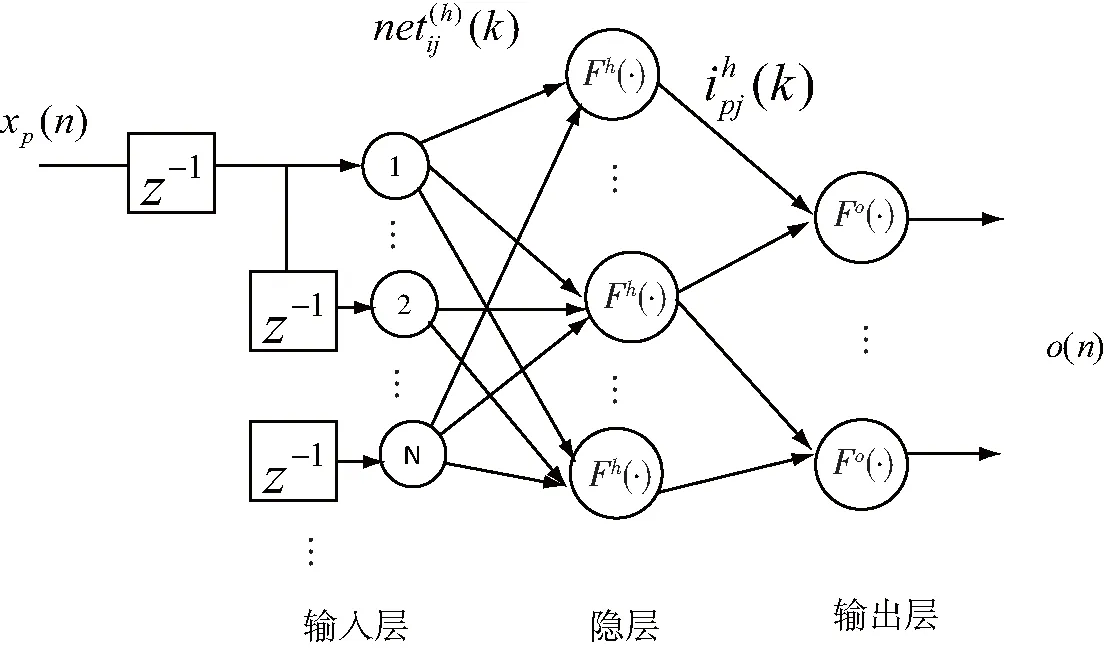
圖1 復值BP神經網絡模型

很多學者研究股票走勢并進行預測。本文在復值BP神經網絡的基礎上進行了改進，利用改進型誤差函數解決傳統復值BP神經網絡中的極限因子問題，從而大大提高了預測精度。

1 復值BP神經網絡模型

復值BP神經網絡是在神經網絡的基礎上延伸的，其結構主要由輸入層、隱層和輸出層構成。復值BP神經網絡模型如圖1所示[2]。通過該模型可以看出,輸入是通過層層遞進的方式向前進行傳播，而且網絡是互相連接的，神經元的輸出也可以理解為下一個神經元的輸入[3]。

2 改進的復值BP神經網絡

2.1 新型誤差函數

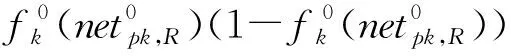
(1)

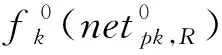
2.2 輸出層權值更新規則

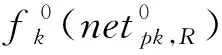
(2)

(3)

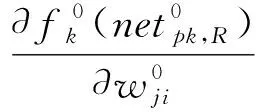
(4)

(5)

(6)

(7)

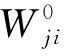
(8)

(9)

根據上式可以得出式(10)。

(10)

將誤差因子代入式(10)，可以得到簡化的方程,如式(11)(12)所示。

(11)

(12)

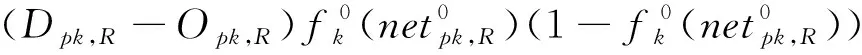
2.3 隱層權值更新規則

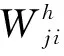
(13)

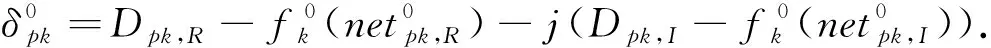
3 改進的復值BP神經網絡在股票中的應用

3.1 數據采集

為了驗證數據的有效性和真實性，筆者通過一年時間對神奇制藥股票價格進行監測和采集，選取在國內外因素影響下沒有發生大的變化的股票作為本實驗數據的數據源。

表1 2016-2017年神奇制藥部分股票信息數據

3.2 數據處理

為了使數據滿足算法的需求，對數據進行映射處理。本文對數據源提供的數據指標進行歸一化，使開盤價格、最高價格、最低價格、收盤價格、交易量幾個指標都在一個可控制的范圍內，加快網絡訓練時間和算法執行效率[5]。將數據樣本通過式(14)進行轉換。

(14)

其中，xi表示數據的輸入，xmax表示最大值，xmin表示數據的最小值，樣本數據的區間取值在[0,1]之間進行波動。

3.3 模型進行定階

股票價格是隨著時間的變化而波動的一種典型的時間樣本。在股票價格預測過程中,關鍵因素是預測模型的定階。本文根據股票價格的特點，采用非線性拓階方法由低到高來確定股票價格模型的階數[6]。首先對樣本數據選取部分數據進行歸一化處理，然后對數據進行拓展階數，運用改進型誤差函數的復值BP神經網絡對拓階的股票價格進行測試，得到股票價格預測模型的均方根誤差。經過多輪的拓階，直到n+1次的拓階產生均方根誤差大于n次拓階的均方根誤差，拓階停止，經過第n次的拓階產生股票價格預測的最優階數[7]。

3.4 建立改進算法的預測模型

設神奇制藥股票收盤價格數據為(x1,x2,…,xn)，改進型誤差函數的復值BP神經網絡對股票價格預測模型的數學關系表達式為：

Xn+1=f(xn，xn-1，…，xn-m).

(15)

其中，Xn+1表示在n+1時間的神奇制藥股票在當天收盤價格預測值，m表示最優階數。神奇制藥股票價格預測模型建立的過程主要有以下幾個方面：

步驟1 對采集的數據進行整理分析，隨機抽取神奇制藥股票收盤價格數據進行歸一化處理。

步驟2 確立模型的階數。運用對非線性數據采用由低到高的拓階方法，將對股票的收盤價格進行階數選擇，建立改進型誤差函數的復值BP神經網絡預測模型，通過式(16)獲取輸入向量和輸出向量。

(16)

步驟3 樣本重構和訓練。將神奇制藥股票的收盤價格的樣本進行重構，生成測試樣本和訓練樣本。

步驟4 預測輸出：通過對訓練樣本的學習獲得的最優模型，對股票收盤價格的樣本進行預測，并對未來該股票收盤價格趨勢進行預判。

步驟5 計算平均相對誤差，如式(17)所示。

(17)

步驟6 計算均方根誤差，從而判斷預測的精度，如式(18)所示。

(18)

神奇制藥股票的收盤價格預測流程如圖2所示。

圖2 神奇制藥股票收盤價格預測流程圖

4 仿真與結果對比分析

4.1 復值BP神經網絡對股票價格預測

首先使用復值BP神經網絡對股票價格進行預測。根據數據源中提供的數據隨機抽取部分數據作為樣本數據，并經過數據的歸一化處理，主要對股票的收盤價進行預測，預測的結果和相對誤差率如表2所示。

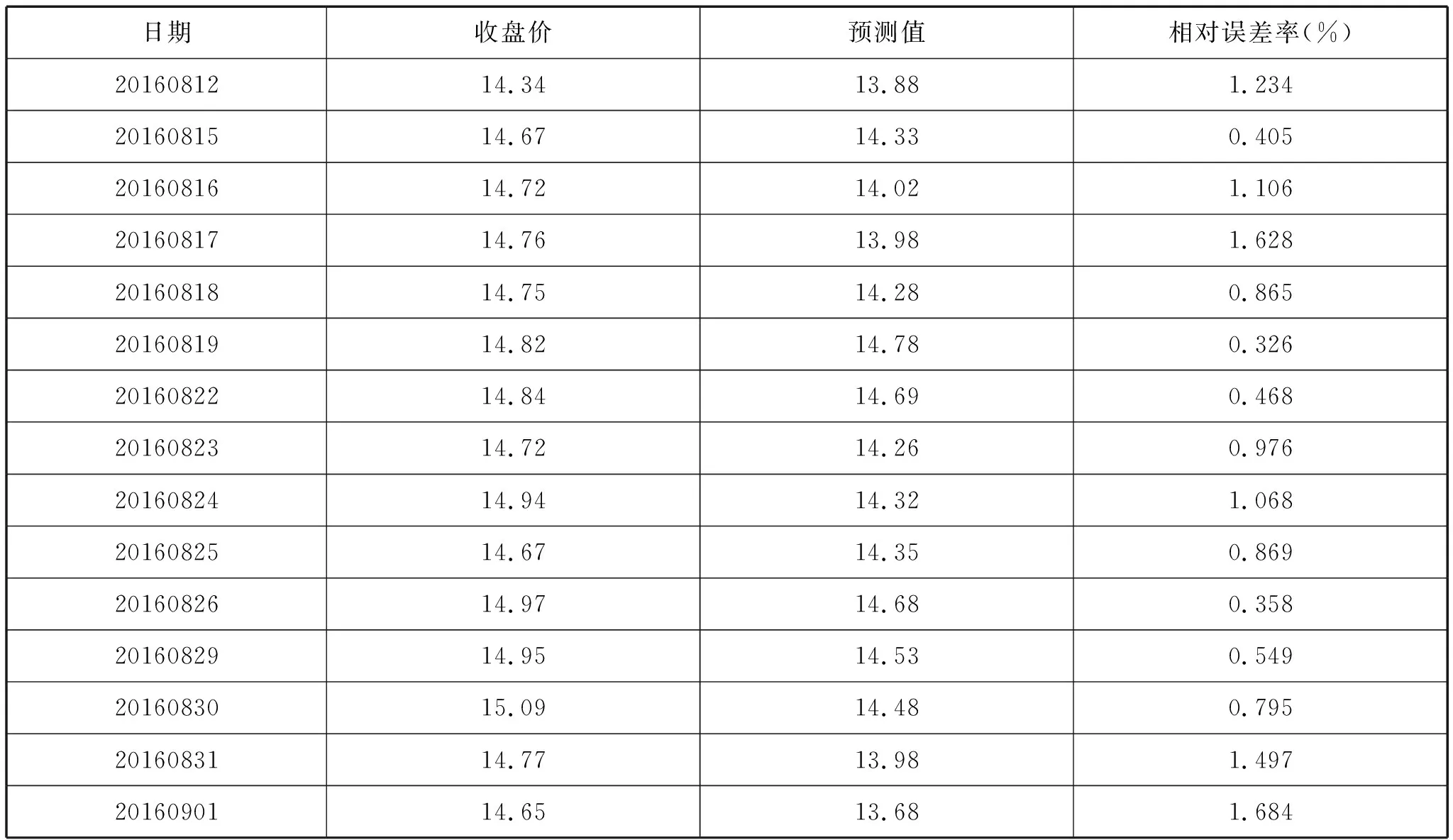
表2 復值BP神經網絡對股票價格預測

4.2 改進的算法的預測

改進型誤差函數對復值BP神經網絡算法中兩個因子的改進，避免了極限情況下神經元產生的誤差，從而提高了神經網絡預測的精度和準確度。通過樣本的選取和重構，經過多次拓階，找到股票價格最優的階數為5。在建立的預測模型中采用動量的梯度下降法的訓練算法對股票的收盤價格進行預測，預測的結果和相對誤差率如表3所示。

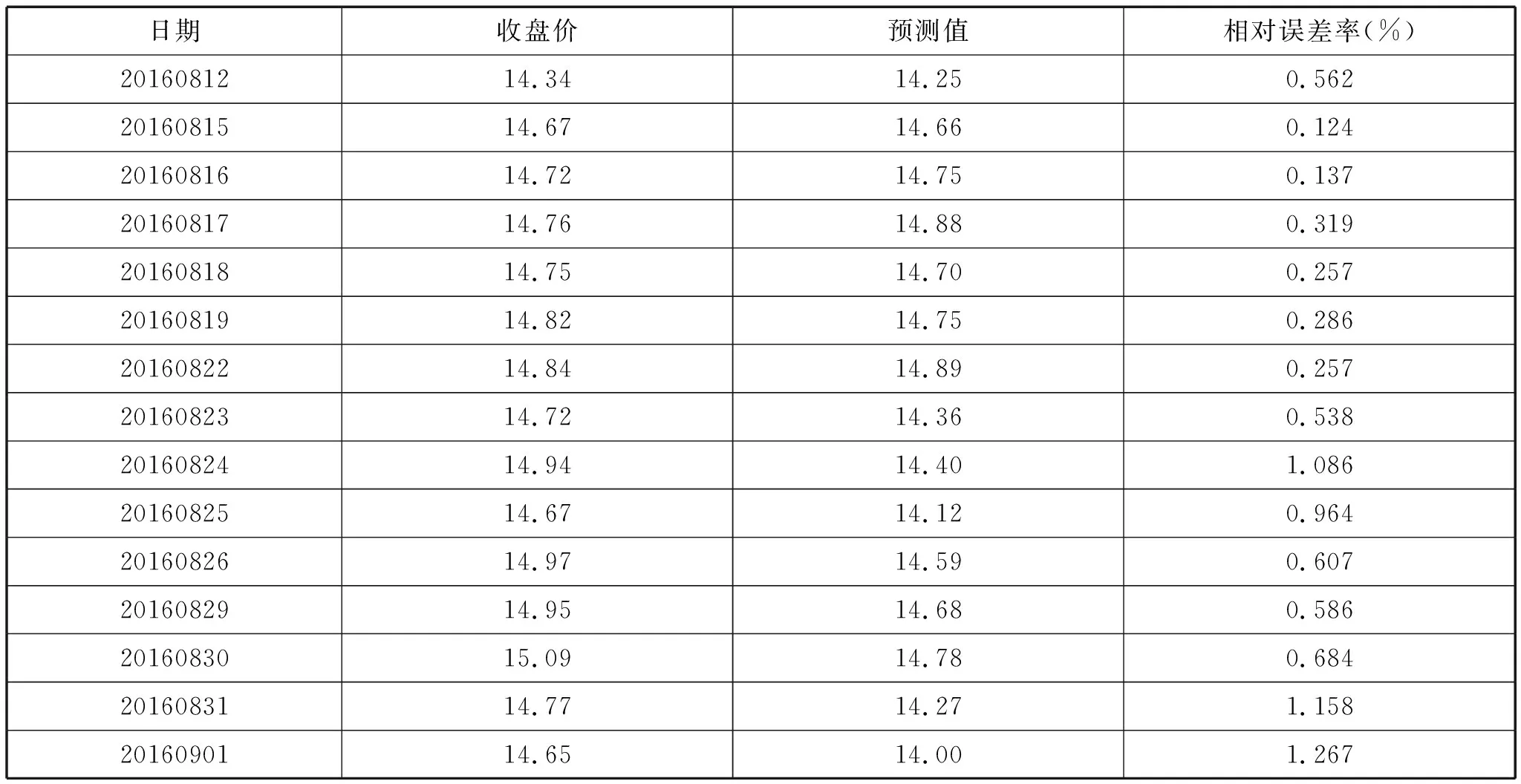
表3 預測結果及相對誤差率

4.3 對比分析

由兩種算法對神奇制藥股票收盤價格的預測值和相對誤差率可以看出，改進的算法具有明顯的優勢：預測精度更為準確，同時降低了相對誤差率，尤其是解決了復值BP神經網絡在極限訓練下的兩個因子對輸出神經元的影響。因此，改進的算法為股票價格的預測提供了技術支持。

5 結語

股票作為金融理財行業中的產品，在我國的金融市場上占有相當重要的地位。科學準確地對股票進行預測不僅可以使投資者減少投資風險，也是政府對股票市場進行宏觀調控的重要依據。本文通過對復值BP神經網絡進行改進，避免了在[0,1]區間的極限產生的誤差，建立了基于改進型函數的復值BP神經網絡預測模型，對神奇制藥股票的收盤價進行了預測。實驗結果表明，改進型函數的復值BP神經網絡比單獨的復值BP神經網絡的預測精度高、收斂速度快，能夠為股票市場的波動趨勢起到預測作用。

[參考文獻]

[1]陳遠,羅必輝,蔣維琛,等.關于股票價格優化預測的建模仿真研究[J].云南大學學報,2016(4):536-542.

[2]楊琦,曹顯兵.基于ARMA_GARCH模型的股票價格分析與預測[J].數學的實踐與認識,2016(6):80-86.

[3]董理,王中卿,熊德意.基于文本信息的股票指數預測[J].北京大學學報,2017(2):273-278.

[4]楊周,劉盼學,王昊,等.應用BP神經網絡分析電主軸頻率可靠性靈敏度[J].哈爾濱工業大學學報,2017(1):30-36.

[5]劉鑫,賈云獻,孫磊,等.基于BP神經網絡的變速箱故障診斷方法研究[J].計算機測量與控制,2017(1):12-15.

[6]王宗杰,邢明峰,王洪泊.基于粒子群優化BP神經網絡的醫患關系風險預警模型[J].北京工業大學學報,2017(1):8-12.

[7]贠海濤,王成振,曹愛霞,等.基于BP神經網絡的電動堆高車貨叉偏載檢測[J].濟南大學學報,2017(2):143-149.