一種牛布魯氏菌病傳播模型的研究

陳珊珊，夏米西努爾·阿布都熱合曼

(新疆大學數學與系統科學學院，新疆烏魯木齊 830046)

[通訊作者]夏米西努爾·阿布都熱合曼(1969- )，女，教授，碩士生導師，從事常微分動力系統研究。

布魯氏病(下文簡稱布病)，是由布魯氏菌病引起的一種人畜共患的急、慢性傳染病.世界動物衛生組織將其列為B類動物疫病，我國將其列為二類動物疫病.動物布病以羊、牛和豬最易感，60余種常見家畜、家禽、野生動物有不同程度的易感性，其特征主要是侵害生殖系統，引起流產、不孕、睪丸炎等.人類布病，其特征為呈現波浪熱、關節痛、睪丸炎等癥狀，以牛型和綿羊型布病最為常見，染病的急性期可以治愈，但不易被認癥，未經治療者的自然病程為3～6個月(平均4個月)，也有的短期1個月或者長達數年.牛型急性期往往不明顯，病期在7～60天，一般為2～3周，少數病人在感染后數月或者1年內發病，嚴重影響人的身體健康.

布病在地中海國家、中東、阿拉伯半島、中南美洲、亞洲和非洲較為常見，數據顯示30%布病患者年齡只有15歲[1-3].在中國，疫區分布廣泛，新疆、內蒙古、吉林、黑龍江、西藏、青海、寧夏、河南等地都受到布魯氏菌病不同程度的感染.近年來，隨著我國家畜飼養量的增加，畜禽的流通日益頻繁，畜間布病疫情相當嚴重[4-6].通過建立和分析相應的布魯氏菌病動力學模型，加強布魯氏菌病的傳染規律和發展趨勢的研究，將有利于布魯氏菌病的控制.

本文首先建立牛布魯氏菌病直接和間接傳播模型，給出基本再生數，并分析該模型的漸近行為，通過數值模擬證明結果的有效性，最后對主要結果進行總結.

1 建立模型

近年來，許多學者關注布魯氏病研究，通過傳染病模型研究菌病傳播，在理論上提出了一系列有效的控制措施[7-14].1994年，Jorge Gonzalez-Guzman和Rual Naulin[15]建立如下牛布魯氏病的動力學模型：

其中，S(t)、I1(t)、I2(t)分別代表易感者類的數量、第一階段染病類的數量、第二階段染病類的數量；θ(t)表示免疫接種的數量.

進一步的，Ainseba[16]考慮直接傳染(接觸傳染)和間接傳染(環境傳染)因素，通過引入被感染的環境項C(t)，建立了具有易感者、染病者和環境中病菌的牛布魯氏菌病動力學模型：

其中，b≥m>0,K>0,p∈[0,1],a1>0,a2>0,k1>0,k2>0.

本文考慮如下模型：

(1)

其中，β1表示直接接觸傳染概率，β2表示間接傳染概率，δ為第一階段染病類到第二階段染病類的轉化率，μi(i=1,2,3)分別表示易感染者、第一階段染病類的、第二階段染病類的死亡率，k1表示菌病的釋放率，k2表示菌病的死亡率，以上參數都是非負的.通過直接計算可得：

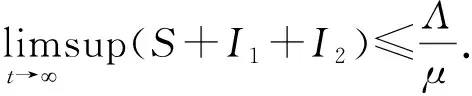
2 基本再生數和平衡點

2.1 基本再生數

(2)

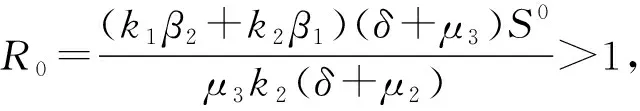
2.2 無病平衡點的穩定性

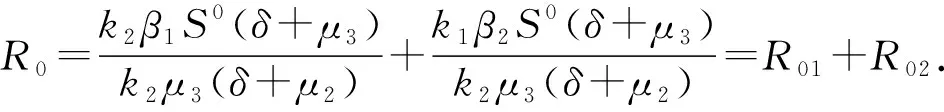
定理1 當基本再生數R0<1時，系統(1)的無病平衡點E0局部漸近穩定.

證明 系統(1)在E0處的特征方程為：

(3)

其中，

直接計算可得：

b1=-β1S0+δ+μ2+μ3+k2

b2=-β2k1S0+k2μ3-δβ1S0+(μ3+k2)(-β1S0+δ+μ2)

b3=k2μ3(-β1S0+δ+μ2)-β2k1S0δ-β2k1S0μ3-β1k2S0δ

>[(δ+μ2)(1-R0)+μ3+k2][k2(δ+μ2)(1-R0)+(1-R0)μ3(δ+μ2)+μ3k2]

即b1>0,b2>0,b3>0,b1b2-b3>0，根據Routh-Hurwitz準則，方程(3)的所有特征值為負.當R0<1時，無病平衡點E0是局部漸近穩定的；當R0>1時，特征多項式具有正根，即E0不穩定.

定理2 當基本再生數R0<1時，系統(1)的無病平衡點E0是全局漸近穩定的.

(4)

沿系統(1)，對W1(t)求導，

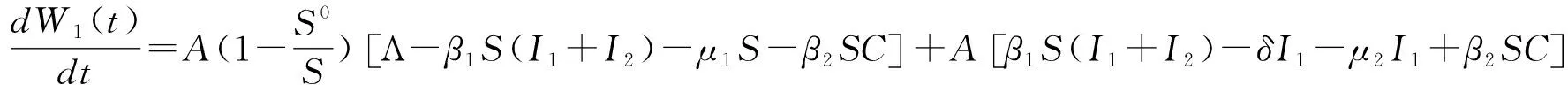
(5)

考慮如下方程：

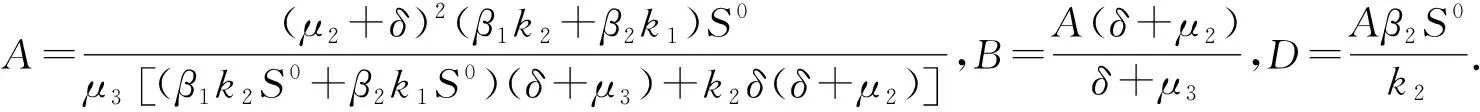
代入方程(5)得到：

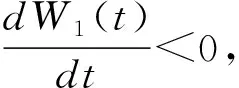
2.3 地方性平衡點的穩定性

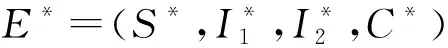
證明 當μ3=μ2時，令I1+I2=I，系統(1)可以轉換為以下形式：

(6)

由此可得模型(6)的特征方程：

(7)

其中，

直接計算可得：

B2=-β2S*(k1I*+k2)+(β1I*+β2C*+μ1)(-β2S*+μ2+k1I*+k2)

+β1S*(β1I*+β2C*)(k1I*+k2)-β2S*k1(1-C*)

B3=(β1I*+β2C*+μ1)(-β2S*+μ2)(k1I*+k2)+(β1I*+β2C*)(k1I*+k2)β1S*

+(β1I*+β2C*)β2S*k1(1-C*)-(β1I*+β2C*+μ1)β2S*k1(1-C*)

B1B2-B3=(a1+μ1+a3+a4)[a4a3+(a1+μ1)(a3+a4)+a1β1S*-a2β2S*]

-(a1+μ1)a4a3-a1a3β1S*-a1a2β2S*

根據Routh-Hurwitz準則，系統(6)特征方程的根都為負，故地方性平衡點E*局部漸近穩定.

3 數值模擬

我們利用數值模擬來探索系統(1)中的易感類，第一階段染病類，第二階段染病類，被污染的環境的動力學模型。通過模型的數據值，驗證地方性平衡點的全局漸近穩定性.假設地方性平衡點的初值(S(0),I1(0),I2(0),C(0))=(200,50,50,0.4)，Λ=400，μ1=0.03，μ2=0.03，μ3=0.4，β1=0.0025，β2=0.0048，δ=0.4，k1=0.002,k2=0.03，通過這些數值計算出R0>1，模擬得出圖1至圖4，驗證了地方性平衡點的全局漸近穩定性。

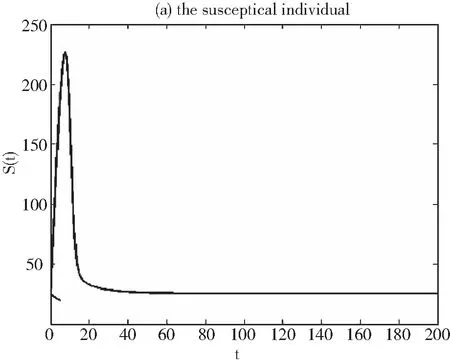
圖1 易感類

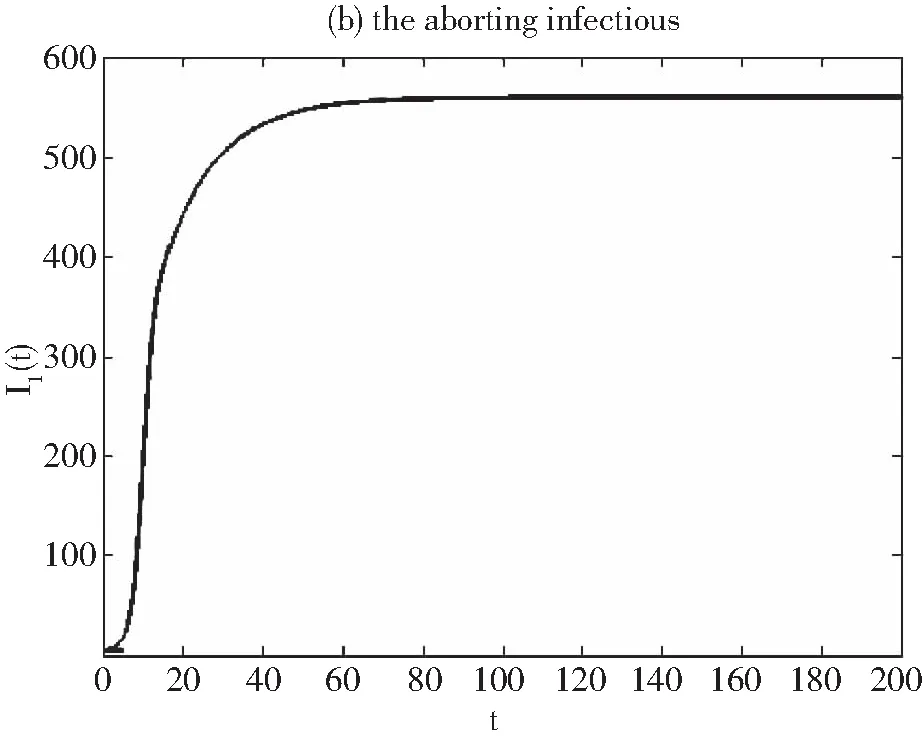
圖2 第一階段染病類

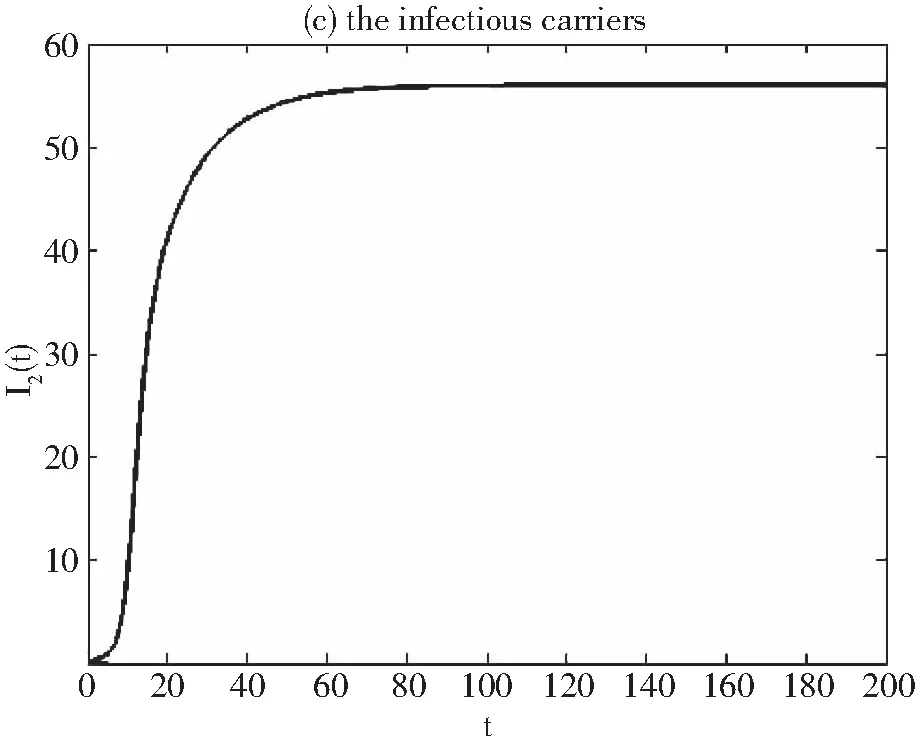
圖3 第二階段染病類

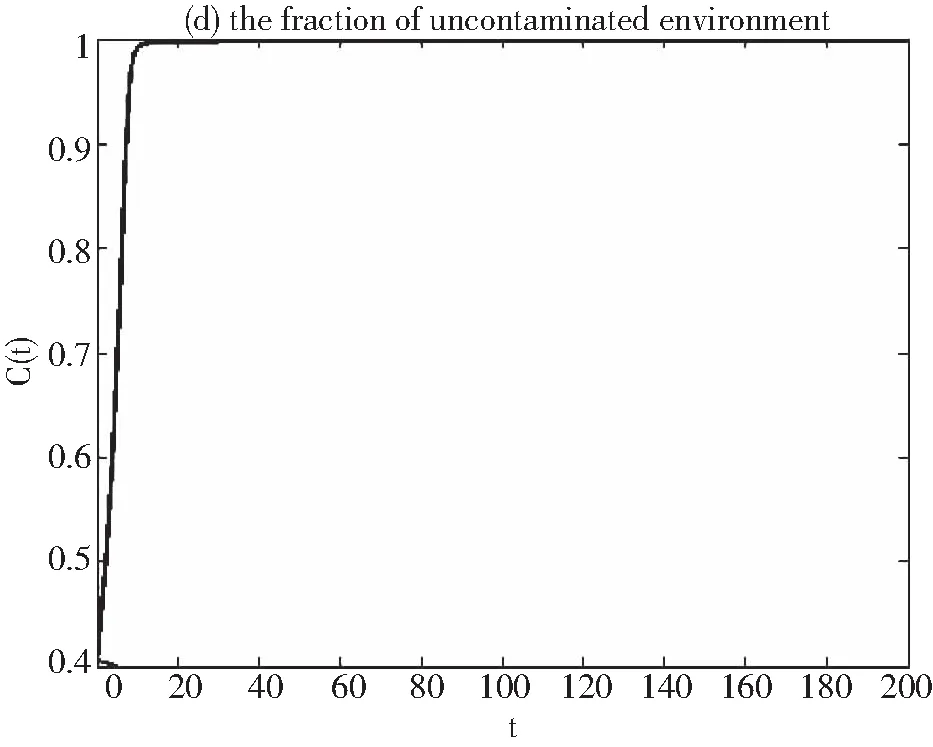
圖4 環境中的病菌

4 結論

與文獻[7,15]相比，本文在系統(1)中討論了一種直接和間接傳播的牛布氏菌病模型，并描述了環境污染率對系統的影響.通過動態分析可以得到，當R0<1時，無病平衡點是全局漸近穩定的，這表明著牛布氏病菌是不活躍的.而當R0>1時，我們在理論上僅僅證明了地方性平衡點的局部漸近穩定性，通過數值模擬圖，當R0>1時，可以看出地方性平衡點是全局漸近穩定的.

[參考文獻]

[1]Roth F,Zinsstag J,Orkhon D,et al.Human health benefits from livestock vaccination for brucellosis:case study[J].Bulletin of the World Health Organization,2003(12):867-876.

[2]M Monir Madkour. Madkour’s Brucellosis[M].Springer Berlin Heidelberg,2001.

[3]Van D P,Watmough J.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Mathematical Biosciences,2002(1-2):29-48.

[4]Benkirane A.Ovine and caprine brucellosis: world distribution and control eradication strategies in West Asia North Africa region[J].Small Ruminant Research,2006(1):19-25.

[5]CUI Buyun.Epidemic surveilance and control of brucellosis in China[J].Transfusion,2000(7):761-70.

[6]Mantur B G,Amarnath S K.Brucellosis in India-a review[J].Journal of Biosciences,2008(4):539-547.

[7]Zinsstag J, Roth F, Orkhon D,et al. A model of animal-human brucellosis transmission in Mongolia[J].Preventive Veterinary Medicine,2005(1-2):77-95.

[8]Lasalle J P.The stability of dynamical systems[J].Society for Industrial and Applied Mathematics,1976(11): 1121-1130.

[9]Sun G Q,Zhang Z K.Global stability for a sheep brucellosis model with immigration[J].Applied Mathematics and Computation,2014(246):336-345.

[10]A H Al-Talafhah,S Q Lafi,Y Al-Tarazi.Epidemiology of ovine brucellosis in Awassi sheep in northern Jordan[J]. Preventive Veterinary Medecine,2003(60):297-306.

[11]R S Cantrell,C Cosner,W F Fagan.Brucellosis,botflies, and brain worms: the impact of edge habitats on pathogen transmission and species extinction[J].J Math Biol,2001(42):95-119.

[12]J Gonzalez-Guzman,R Naulin.Analysis of a model of bovine brucellosis using singularperturbations[J].J Math Biol,1994(33):211-234.

[13]J Mc Given.The improved specificity of bovine brucellosis testing in Great Britain[J]. Research in Veterinary Science,2008(84):38-40.

[14]J B Muma,N Toft,J Oloya,et al.Evaluation of three serological tests for brucellosis in naturally infected cattle using latent class analysis[J].Veterinary Microbiology,2007(125):187-192.

[15]González-Gunmán J, Naulin R. Analysis of a model of bovine brucellosis using singular perturbations[J]. Journal of Mathematical Biology,1994(2):211-223.

[16]Ainseba B, Benosman C, Magal P.A model for ovine brucellosis incorporating direct and indirect transmission[J]. J Biol.Dyn,2010(1):2-11.